Complete Solutions to EXAMPLE of chapter CONTINUITY & DIFFERENTIABILITY of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | CONTINUITY & DIFFERENTIABILITY |
| MAXIMUM PUBLICATION | EXAMPLE |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Consider the function `g(x)=abs(x-2)/(x-2)`
Find the domain and range of the function
`g(x)` .
View SolutionConsider the function `g(x)=abs(x-2)/(x-2)`
check whether the g(x) is continuous at `x=2` .
View SolutionIf `f(x)=x+abs(x)+1` , then which of the follow represents `f(x)`
View SolutionIf `f(x)=x+abs(x)+1`
``test`` whether ``f(x)`` ``is`` ``continous at `x=0` Explain.
View SolutionConsider the function `f(x)={(sinx/x, x<0),(x+1,xge0):}`
Find `lim_(xrarr0)f(x)`
View SolutionConsider the function `f(x)={(sinx/x, x<0),(x+1,xge0):}`
Is `f(x)` continuous at `x=0` ?
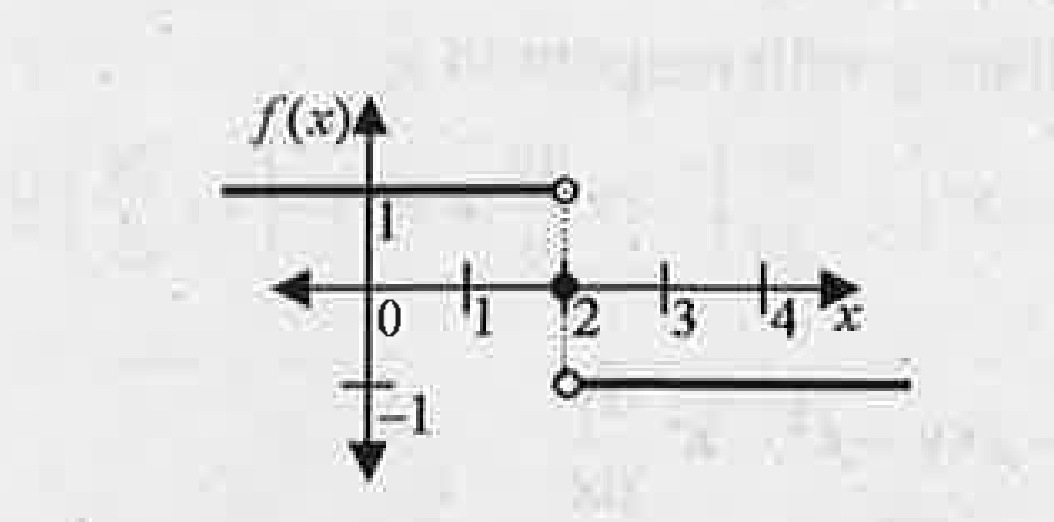
View SolutionConsider the figure and answer the question.
Identify the graphed function.
`f(x)=abs(x)/x`
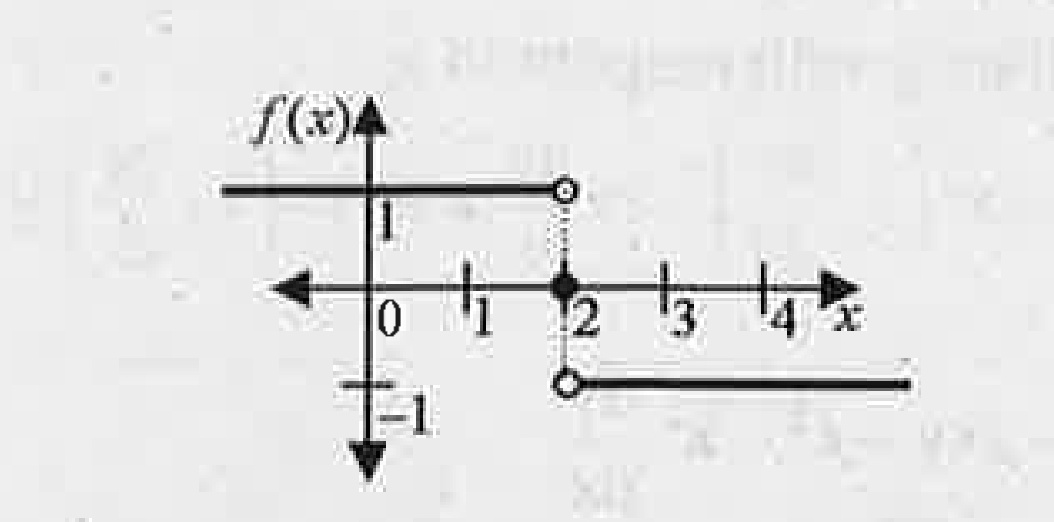
View SolutionConsider the figure and answer the question.
Identify the graphed function.
`f(x)={(abs(x-2)/(x-2),xne2),(0,x=2):}`
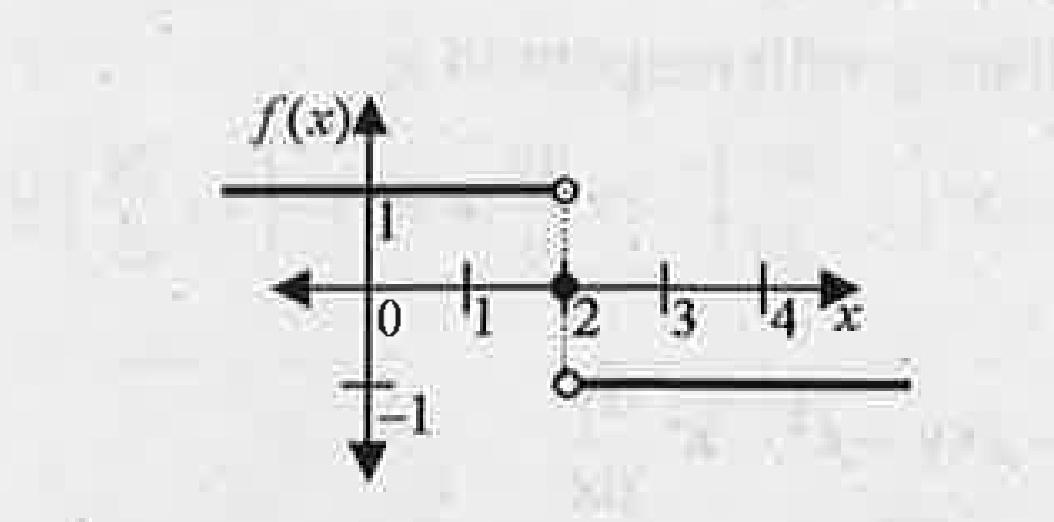
View SolutionConsider the figure and answer the question.
Identify the graphed function.
`f(x)={(abs(x+2)/(x+2),xne2),(0,x=2):}`
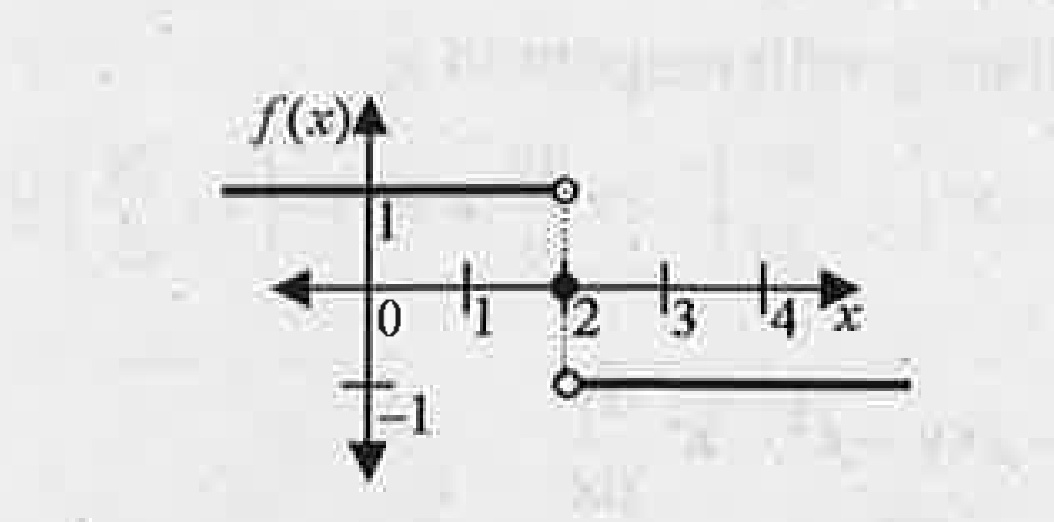
View SolutionConsider the figure and answer the question.
Identify the graphed function.
`f(x)=abs(x-1)/(x-1)`
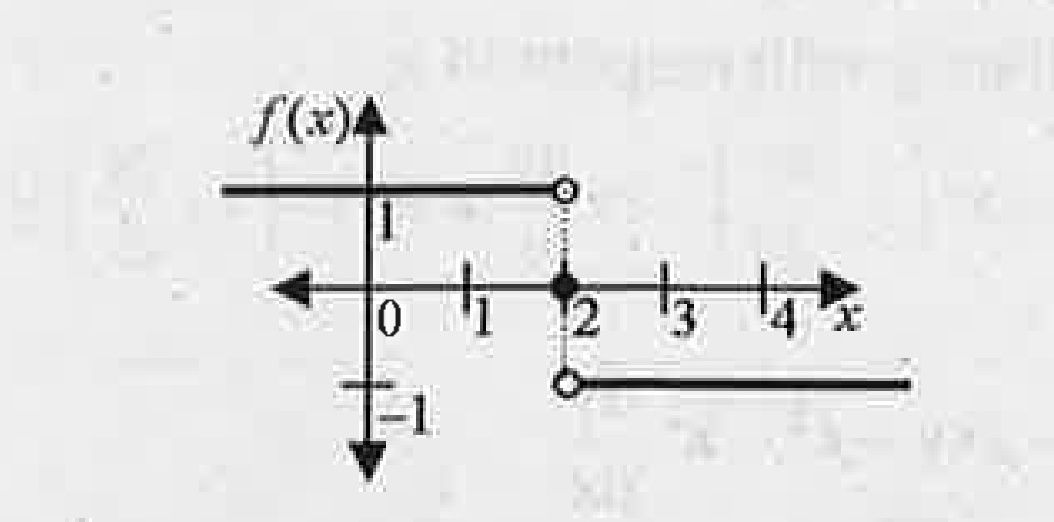
View SolutionConsider the figure and answer the question.
Discuss the continuity of the above function at `x=2` .
View SolutionConsider `f(x)={(2x,if,x<2),(2,if,x=2),(x^2,if,x>2):}`
Find `lim_(xrarr2^-)f(x)` and `lim_(xrarr2^+)f(x)`
View SolutionConsider `f(x)={(2x,if,x<2),(2,if,x=2),(x^2,if,x>2):}`
`f(x)` is continuous . If not so, how can you make it continuous.
View SolutionIf `y=log_(10)x+log_(x)10+log_(x)x+log_(10)10`
then `dy/dx`= ?
View SolutionExamine the continuity of the function `f(x)={(x+1,xge1),(x^2+1,x<1):}`
View SolutionFind `dy/dx` of the following
`2x+3y=sinx`
View SolutionFind `dy/dx` of the following
`xy+y^2=tanx+y`
View SolutionFind `dy/dx` of the following
`x^3+x^2y+xy^2+y^3=81`
View SolutionFind `dy/dx` of the following
`sin^2x+cos^2y=1`
View SolutionFind `dy/dx` of the following
`sqrtx+sqrty=1`
View SolutionFind `dy/dx` of the following
`x^2+xy+y=100`
View SolutionFind `dy/dx` of the following
`x^2(x-y)=y^2(x+y)`
View SolutionFind `dy/dx` of the following
`xy^2+x^2y=2`
View SolutionFind `dy/dx` of the following
`siny=xcos(a+y)`
View SolutionFind `dy/dx` of the following
`y=sin^(-1)((2x)/(1+x^2))`
View SolutionFind `dy/dx` of the following
`y=tan^(-1)((3x-x^3)/(1-3x^2))`
View SolutionFind `dy/dx` of the following
`y=sin^(-1)((1-x^2)/(1+x^2))`
View SolutionFind `dy/dx` of the following
`y=sec^(-1)((1)/(2x^2-1))`
View SolutionFind `dy/dx` of the following
`y=tan^(-1)sqrt((1-cosx)/(1+cosx))`
View SolutionFind `dy/dx` of the following
`y=cos^(-1)frac((x-x^(-1)))(x+x^-1)`
View SolutionFind `dy/dx` of the following
`sin^(-1)[xsqrt(1-x)+sqrtxsqrt(1-x^2)]`
View SolutionFind `dy/dx` of the following
`x=a(t-sint)` , `y=a(1-cost)`
View SolutionFind `dy/dx` of the following
`y=e^tcost` , `x=e^tsint`
View SolutionIf `y=log(1/x)` , show that `dy/dx+e^y=0`
View SolutionIf `e^y(x+1)=1` . Show that
`dy/dx=-e^y`
View SolutionIf `e^y(x+1)=1` . Show that
`(d^2y)/dx^2=(dy/dx)^2`
View SolutionEvalute `lim_(xrarr0)frac(kcosx)(pi-2x)`
(Hint: Put `pi`-2x=y , where k is a constant.)
View SolutionFind the value of k if `f(x)` is a continious function give by
`f(x)={((kcosx)/(pi-2x),xnepi/2),(3,x=pi/2):}` at `x=pi/2`
View SolutionIf `f(x)={(x-absx,x<2),(0,x=2),(3x-5,x>2):}`
Find `lim_(xrarr2)f(x)`
View SolutionIs `f(x)` =`x^2`continuous at `x=2` ?
View SolutionIf `x=2costheta` , `y=3sintheta`
Find `dy/dx` .
View SolutionIf `x=2costheta` , `y=3sintheta`
Find `(d^2y)/(dx^2)` .
View SolutionIf `y=(tan^(-1)x)^2`, show that
`(x^2+1)^2y_2+2x(x^2+1)y_1=2` .
View SolutionFind `dy/dx` If `y=sin^(-1)(frac(1-x^2)(1+x^2))` , `0 < x < 1`
View SolutionLet f(x)=`{(cosx,0lexlec),(sinx,c Find the value of c if `f` is continuous on `[0,pi]` .
View SolutionFind `dy/dx` if `x=2sintheta` , `y=3costheta`
View SolutionExamine whether the function defined by
`f(x)={(x+5,xle1),(x-5,x>1):}` is continuous or not .
View SolutionIf `x=a^(sin^(-1)t)` , `y=a^(cos^(-1)t)` , `a>0` , show that
`dy/dx=-y/x`
View SolutionIf `f(x)={(1-x,0
View SolutionIf `(1, xle 3)`, `(ax+b`, `3 find `f(3^+)` and `f(3^-)`
View SolutionIf `{(1,xle3)`, `(ax+b,3 hence find the value of 'a' and 'b' so that `f(x) is continuous.
View SolutionConsider `f(x)={(2x+3,xle2),(x+2k,x>2):}`
Find `f(2)`
View SolutionConsider `f(x)={(2x+3,xle2),(x+2k,x>2):}`
Evalute `lim_(xrarr2^+)f(x)`
View SolutionConsider `f(x)={(2x+3,xle2),(x+2k,x>2):}`
Find the value of k, if is continious at `x=2` .
View SolutionFind `dy/dx` if
`y=(logx)^cosx`
View SolutionFind `dy/dx` of
`x=2at^2` , `y=at^4`
View SolutionFind `dy/dx` of
`x=a(costheta+thetasintheta)` , `y=a(sintheta-thetacostheta)`
View SolutionFind `dy/dx` of
`y=x^x`
View SolutionFind `dy/dx` of
`y=(xlogx)^log(logx)`
View SolutionFind `dy/dx` of
`y=sqrt(sinx +sqrt (sinx+sqrt(sinx+.....`
View SolutionFind `dy/dx` of
`y^x=x^(siny)`
View SolutionFind `dy/dx` of
`y=(logx)^x+x^(logx)`
View SolutionFind `dy/dx` of
`y=(sinx)^x+sin^(-1)sqrtx`
View SolutionFind `(d^2y)/(dx^2)`
`y=x^2+3x+2`
View SolutionFind `(d^2y)/(dx^2)`
`y=tan^(-1)x`
View SolutionMatch the following.
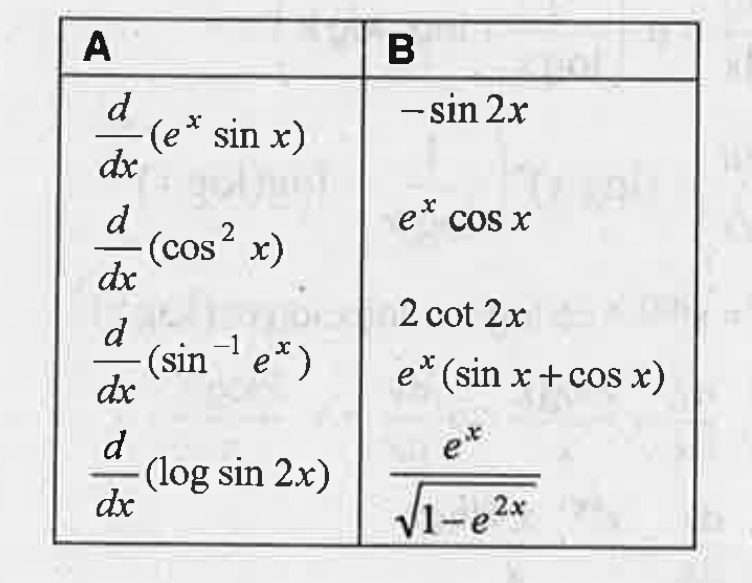
View SolutionIf `x=sint` and `y=sinmt` show that
`y=sin(msin^(-1)x)`
View SolutionIf `x=sint` and `y=sinmt` show that
`dy/dx=`
View SolutionIf `x=sint` and `y=sinmt` show that
`(1-x^2)y_2-xy_1+m^2y=0`
View SolutionConsider the function
`f(x)=x(x-2)` , `x in[1,3]`
Verify mean value theorem for the function in `[1,3]` .
View SolutionVerify Lagranges' Mean value theorem for the function `f(x)=2x^2-10x+29` in `[2,9]`
View SolutionLet `f(x)=x(x-1)(x-2)` , `x in [0,2]`
Find `f(0)` and `f(2)`
View SolutionLet `f(x)=x(x-1)(x-2)` , `x in [0,2]`
Find `f^'(x)`
View SolutionLet `f(x)=x(x-1)(x-2)` , `x in [0,2]`
Find thevalues of x where `f^'(x)=0` verify Rolle's theorem.
View SolutionVerify Rolle's Theorem for the function
`f(x)=x^2+2x-8` , `x in [-4,2]`
View SolutionExamine that Rolle's Theorem is applicable to the function in the given intervals , justify your answer .
`f(x)=[x]` , `x in [5,9]`
View SolutionExamine that Rolle's Theorem is applicable to the function in the given intervals , justify your answer .
`f(x)=x^2-1` , `x in [1,2]`
View SolutionExamine the continuity of the function
`f(x)={(absx+3,,xle-3),(-2x,,-3
View SolutionTest continuity for the folowing functions.
`f(x)={(xsin(1/x), x ne0),(0,x=0):}` at `x=0`
View SolutionTest continuity for the folowing functions.
`f(x)={(2^(1/x), x ne0),(3,x=0):} at `x=0`
View SolutionTest continuity for the folowing functions.
`f(x)={((x^2-4x+3)/(x^2-1), x ne1),(2,x=1):}` at `x=1`
View SolutionIf `y=sin^(-1)x/sqrt(1-x^2)` prove that
`(1-x^2)y^2=(sin^(-1)x)^2`
View SolutionIf `y=sin^(-1)x/sqrt(1-x^2)` prove that
`(1-x^2)y_1-xy=1`
View SolutionIf `y=sin^(-1)x/sqrt(1-x^2)` prove that
`(1-x^2)y_2-3xy_1-y=0`
View SolutionAt what point on the curve `y=x^2` , `x in [-2,2]` at which the tangent is parallel to x-axis?
View SolutionIf `f(x)=(sqrt((1+px))-sqrt((1-px)))/x` , `-1lex<0`
`=(2x+1)/(x-2)` , `0lexle1`
is continuous in the interval `[-1,1]` .
Find `lim_(xrarr0)f(x)`
View SolutionIf `f(x)=(sqrt((1+px))-sqrt((1-px)))/x` , `-1lex<0`
`=(2x+1)/(x-2)` , `0lexle1`
is continuous in the interval `[-1,1]` .
Find P.
View SolutionIf `f(x)=(sqrt((1+px))-sqrt((1-px)))/x` , `-1lex<0`
`=(2x+1)/(x-2)` , `0lexle1`
is continuous in the interval `[-1,1]` .
Find P.
View SolutionIf `ax^2+2hxy+by^2=1`
Find `dy/dx`
View SolutionIf `ax^2+2hxy+by^2=1`
Find `(d^2y)/(dx^2)`
View SolutionConsider the function `y=x^xsqrtx`
Express the above function as `logy=(x+1/2)logx`
View SolutionConsider the function `y=x^xsqrtx`
Find `dy/dx`
View SolutionVerify mean value theorem for the function
`f(x)=(x-2)^2` in `[1,4]` .
View SolutionFind a point on the curve `y=(x-2)^2` at which the tangent is parallel to the chord joining the points `(1,1)` and `(4,4)`
View SolutionFind a point on the curve `y=(x-2)^2` at which the tangent is parallel to the x-axis .
View SolutionDifferentiate `x^(sinx)` w.r.t. x
View SolutionIf `x=at^2` , `y=2at` , then find `dy/dx` .
View SolutionIf `y=sin^(-1)(cosx)+cos^(-1)(sinx)` , then find `dy/dx` .
View SolutionDifferentiate `(x-1)/(x-3)` with respect to x .
View SolutionDifferentiate `sqrt(((x-1)(x-2))/((x-3)(x-4)(x-5)` with respect to x.
View Solution
EXAMPLE questions and complete solutions for chapter CONTINUITY & DIFFERENTIABILITY of MAXIMUM PUBLICATION of Class 12