Complete Solutions to Exercises (Level 1 Single Correct Answer) of chapter PROBABILITY of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | PROBABILITY |
| MCGROW HILL PUBLICATION | Exercises (Level 1 Single Correct Answer) |
| Number Of Questions | 65 |
| Academic Year | 2023-24 |
A bag contains 100 tickets numbered 1 to 100. If one ticket is picked up at random, then the probability that the number is divisible by 3 or 5 is
View SolutionSuppose n students appear in an examination. Let X = the number of students who pass the examination. Suppose `P(X=k)=lambdak^2`, then value of `lambda` is
View SolutionSuppose two numbers a and b are chosen randomly from the set {1, 2, 3, 4, 5, 6}. The probability that function `f(x) = x^3+ ax^2 + bx` is strictly increasing function on R is:
View SolutionTwo dice are rolled together and the numbers x, y on them form complex number z = x + iy. The probability that `|z| le 3` is
View SolutionSuppose A is an event which is independent of itself and B is any other event, then
View SolutionSix boys and six girls sit in a row randomly. Find the probability that (i) the six girls sit together, (ii) the boys and girls sit alternately.
View SolutionIf `P(AnnB)=1/2,P( A nn B )=1/3, P(A)=p , P(B)=2p ,` then find the value of `pdot`
View SolutionOut of 20 consecutive integers, two are chosen at random. The probability that their product is odd is
View SolutionAn experiment has 10 equally likely outcomes. Let A and B be two non-empty events of the experiment. If a consists of 4 outcomes, the number of outcomes that B must have so that A and B are independent , is
View SolutionA box contains 24 identical balls of which 12 are white and 12 are black. The balls are drawn at random from the box one at a time with replacement. The probability that a white ball is drawn for the 4th time on the 7th draw is `5//64` b. `27//32` c. `5//32` d. `1//2`
View SolutionIndia plays two matches each with West Indies and Australia. In any match the probabilities of India getting points `0, 1 and 2` are `0.45, 0.05 and 0.50` respectively. Assuming that the outcomes are independent, the probability of India getting at least 7 points is (a) `0.8750` (b) `0.0875` (c) `0.0625` (d) `0.0250`
View SolutionIf E and F are two events associated with a random experiment for which P(E)=0.6, `P(E uu F)=0.85` and `P(E nn F)`=0.42 , then P(F) is
View SolutionIf E and F are events with P(E) `le` P(F) and P(E `nn` F) `gt` 0, then
View SolutionIf the integers m and n are chosen at random between 1 and 100, then the probability that a number of the form `7^(m) + 7^(n)` is divisible by 5, equals :
View SolutionThe probabilities that a student passes in Mathematics, Physics and Chemistry are m, p and c respectively. Of these subjects the student has 75% chance of passing in at least one subject, 50% chance of passing in at least two and 40% chance of passing in exactly two. which is true?
View SolutionOne ticket is selected at random from 100 tickets numbered 00, 01, 02,.., 99. Suppose A and B are the sum and product of the digit found on the ticket. Then `P(A=7//B=0)` is given by
View SolutionA mapping is select at random from the set of all the mappings of the set `A={1,2, n}` into itself. Find the probability that the mapping selected is an injection.
View SolutionA natural number is chosen at random from the first 100 natural numbers. The probability that `x+(100)/x > 50` is `1//10` b. `11//50` c. `11//20` d. none of these
View SolutionA bag contains `(2n+1)` coins. It is known that `n` of these coins have a head on both sides whereas the rest of the coins are fair. A coin is picked up at random from the bag and is tossed. If the probability that the toss results in a head is `(31)/(42)` , determine the value of `n` .
View SolutionIf `X and Y` are independent binomial vatiates `B(5,1/2) and B(7,1/2)` and the value of `P(X+Y=3)` is
View SolutionSuppose n (`ge` 3) persons are arranged in a row. The probability that two particular persons are not together is
View SolutionA number x is chosen at random from the set {1, 2, 3, ...., 100). Let p = probability that x is divisible by 19 and q = probability that x is divisible by 31, then p + q is equal to
View SolutionIf the letters of the word PROBABILITY are written down at random in a row, the probability that two B-s are retogether is
View SolutionIf four positive integers are taken at random and multiplied together, then the probability that the last digit is 1, 3, 7 or 9 is
View SolutionTwo contestants play a game as follows: each is asked to select a digit from 1 to 9. If the two digits match they both win a prize. The probability that they will win a prize in a single trial is
View SolutionIf A and B are two events, then which of the following does not represent the probability that exactly one of A, B occurs is
View SolutionIf A and B are two events, then which one of the following is/are always true?
View SolutionA sum of money is rounded off to the nearest rupee, find the probability that the round off error is at least ten paise.
View SolutionAn electric bulb will last for 150 days or with a probability 0.7 and it will last formost 160 days with probability 0.8.probability that the bulb will last between 150 and 160 days is
View SolutionIn a bag there are three tickets numbered 1,2,3. A ticket is drawn at random and put back, and this is done four times. The probability that the sum of the numbers is even, is
View SolutionTwo natural numbers x and y are chosen at random from the set `{1,2,3,4,...3n}`. find the probability that `x^2-y^2` is divisible by 3.
View SolutionThree persons A, B and C are to speak at a function along with 7 other persons. The probability that A, B, and C speak together
View SolutionA positive integer is chosen at random. The probability that the sum of the digits of its square is 33 is
View SolutionConsider a lottery that sells `n^2` tickets and awards n prizes. If one buys n tickets the probability of A his winning is i.e., getting at least one prize is
View SolutionLet x be a non-zero real number. A determinant is chosen from the set of all determinants of order 2 with entries x or -x only. The probability that the value of the determinant is non-zero is
View SolutionA dice is rolled three times, find the probability of getting a larger number than the previous number each time.
View SolutionIf `(1+4p)/(4),(1-p)/(3) and (1-2p)/(2)` are the probabilities of three mutually exclusive events then values of p may be
View SolutionTwo non negative integers are chosen at random. The probability that the sum of the square is divisible by 10, is
View SolutionA is a set containing n elements. Two subsets P and Q of A are chosen at random. (P and Q may have elements in common). The probability that `P nn Q= phi` is
View SolutionSuppose A is a set containing n elements. Two subsets P and Q of A are chosen at random. If the probability that P is a subset of Q is 243/1024, then n is equal to
View SolutionThree of six vertices of a regular hexagon are chosen at random. The probability that the triangle with three vertices is equilateral is `1//2` b. `1//5` c. `1//10` d. `1//20`
View SolutionEach of the `n` urns contains 4 white and 6 black balls. The `(n+1)` th urn contains 5 white and 5 black balls. One of the `n+1` urns is chosen at random and two balls are drawn from it without replacement. Both the balls turn out to be black. If the probability that the `(n+1)` th urn was chosen to draw the balls is 1/16, then find the value of `n` .
View SolutionTwo integers x and y are chosen with replacement out of the set {0, 1, 2, . . . 10}. The probability that |x - y| doesn't exceed 5 is
View SolutionIn a test, an examinee either guesses or copies or knows the answer to a multiple choice question with four choices. The probability that he makes a guess is 1/3 and the probability that he copies the answer is p. The probability that his answer is correct, given that he copied it, is 1/8. If the probability that he knew the answer to question, given that he correctly answered is 8/11, then value of p is
View SolutionAn unbiased coin is tossed n times. Let X denote the number of times head occurs. If `P(X=4), P(X=5) and P(X=6)` are in A.P, then the value of n can be
View SolutionA fair coin is tossed at a fixed number of times.If the probability of getting exactly 3 headsequals the probability of getting exactly 5 heads, then the probability of getting exactlyone head is
View SolutionLet `E^(@)` denotes the complement of an event E. If E, F, G are pairwise independent events with `P(G) gt 0` and `P (E nn F nn G) =0`. Then, `P(E^(@) nn F^(@)|G)` equals :
View SolutionIf P (E) = 0.40, P (F) = 0.35, P (E`uu`F) = 0.55, then P(F/E) is
View SolutionThe mean and variance of a binomial distribution are 4 and 4/3 respectively, find `P(Xgeq1)dot`
View SolutionThere are 20 cards. Ten of these cards have the letter `"I"` printed on them and the other 10 have the letter `"I"` printed on them. If three cards picked up at random and kept in the same order, the probability of making word IIT is `1//9,1//3` b. `1//16 ,1//4` c. `1//4,1//2` d. none of these
View SolutionA and B toss a coin alternately till one of them gets a head and wins the game. If A starts the game, find the probability that B will win the game.
View SolutionA fair coin is tossed repeatedly. If head and tail appear alternatively on first 7 tosses, then the probability that head appears on the eighth toss is
View SolutionIf P(A) `gt` 0, then the event A is independent of itself if and only if P(A) is
View SolutionIf A and B are two events, then `P(A uu B)=P(A nn B)` if and only if
View SolutionA dice is thrown. The probability that the first time 1 occurs at the even throw is
View SolutionIf A and B are two events such that `P(A) ne 0` and `P(B) ne 1` then `P((barA)/(B))`
View SolutionTwo unbiased die are rolled together . Let A={(a,b): a+b=11} and B= { (a,b): a `ne` 5}, then P(A|B) equals
View SolutionA bag contains w white and b black balls. A ball is drawn at random and put back in the bag with k additional balls of the same colour. A ball is again drawn at random from the bag. The probability that it is black is
View SolutionThe probability distribution of a random variable X is given as follows:

If E(X)=2.3 , then value of k is
View SolutionLet A and B be two events such that P(A|B) = P(A'|B') = p and P(B) = 0.05. The value of p so that P(B|A) =0.9 is
View SolutionIn the Fig. 24.10 the number represents the probability of the event. Which one of following is not true ?
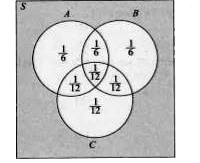
View SolutionIf three numbers are selected from the set of the first 20 natural numbers, the probability that they are in GP, is
View SolutionFrom a bag containing 30 tickets numbered 1, 2, 3, ... 30, three tickets are selected at random without replacement. Suppose these tickets are arranged as `x_1 lt x_2 lt x_3`. The probability that `x_2` = 15 and `x_3 gt 20`, is
View SolutionSuppose an unbiased die has n sides numbered i = 1, 2, ... n. The die is tossed n times (assume independence) and a "match" is defined to be the occurrence of side i on the its roll. The probability of at least one match is
View SolutionThree numbers are chosen at random (without replace ment) from the numbers 1, 2,... 20. The probability that the numbers are not consecutive are
View Solution
Exercises (Level 1 Single Correct Answer) questions and complete solutions for chapter PROBABILITY of MCGROW HILL EDUCATION MATHS (HINGLISH) of Class 12
All Exercises from MCGROW HILL PUBLICATION Class 12 MATHS PROBABILITY
- Exercises (Level 1 Single Correct Answer)
- Exercises (Level 2 Single Correct Answer)
- Exercises (Numerical Answer)
- Exercises (Single Correct Answer)
- Previous Years AIEEE/JEE Main Papers
- Previous Years B-Architecture Entrance Examination Papers
- Solved Examples (Level 1 Single Correct )
- Solved Examples (Level 2 straight Objective Correct )
- Solved Examples (Numerical Answer )
- Solved Examples (Single Correct )