Complete Solutions to Solved Examples (Level 1 Single Correct ) of chapter PROBABILITY of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | PROBABILITY |
| MCGROW HILL PUBLICATION | Solved Examples (Level 1 Single Correct ) |
| Number Of Questions | 80 |
| Academic Year | 2023-24 |
Suppose A and B are two events such that `0 lt P(B) lt 1`. If `P(A|B')=(P(A))/(1-P(B))` then which one of the following is not true?
View SolutionA man is known to speak truth 3 out of 4 times. He takes out a card at random from a well shuffled pack of 52 playing cards, and reports it is a king. The probability that its actually a king is
View SolutionSuppose A has 7 fair coins and B has 6 fair coins. If A and B toss these coins simultaneously, then the probability that A and B get equal number of heads is
View SolutionA box X contains 1 white ball, 3 red balls and 2 black balls. Another box Y contains 2 white balls, 3 red balls and 4 black balls. If one ball is drawn from each of the two boxes, then the probability the balls are of different colours is
View SolutionA sample consists of six points S={(I,j)|i=1,2,j=1,2,3}. Suppose P((I,j)) =`k/(i+j)`. Let A = {(I,j)|i+j=4} and B={(I,j)|j=2} , then P(B|A) is equal to
View SolutionLet A be a set consisting of n elements. The probability of selecting two subsets P and Q of set A such that `Q= overline(P)`, is
View SolutionFour natural numbers are selected at random and are multiplied. The probability that the product is divisible by 5 or 10 is
View SolutionSix boys and six girls sit in a row randomly. Find the probability that (i) the six girls sit together, (ii) the boys and girls sit alternately.
View SolutionAn unbiased die is thrown twice. Let the event A be "odd number on the first throw" and B the event "odd number on the second throw". Check the independence of the events A and B.
View SolutionTwo events `Aa n dB` have probabilities 0.25 and 0050, respectively. The probability that both `Aa n dB` occur simultaneously is 0.14. then the probability that neither `A` nor`B` occurs is a. 0.39 b. 0.25 c. 0.11 d. none of these
View SolutionAn anti-aircraft gun can take a maximum of four shots at an enemy plane moving away from it. The probability of hitting the plane at the first, second, third and fourth shots are `0.4, 0.3, 0.2` and `0.1`, respectively, What is the probability that the plane is hit when all the four shots are fired? (A) `0.4379` (B) `0.6872` (C) `0.6976` (D) `0.3507`
View Solutionare two candidates seeking admission in I.I.T. The probability that P is selected is 0.5 and the probability that both are selected is at most 0.3. Prove that the probability of being selected is at most 0.8
View SolutionIf the letters of the word ASSASSIN are written down in a row, the probability that no two S's occur together, is
View SolutionFifteen coupons are numbered 1, 2, 3,…, 15 respectively. Seven coupons are selected random one at a time with replacement. The probability that the largest number appearing on the selected coupons is atmost 9, is :
View SolutionA student appears for tests I, II and III. The student is successful if the passes either in tests I and II or tests I and III. The probabilities of the student passing in tests I, II and III are p,q and `(1)/(2)`, respectively. If the probability that the student is successful, is `(1)/(2)`, then
View SolutionA bag contains `a` white and `b` black balls. Two players, `Aa n dB` alternately draw a ball from the bag, replacing the ball each time after the draw till one of them draws a white ball and wins the game. `A` begins the game. If the probability of `A` winning the game is three times that of `B ,` then find the ratio `a : b`
View SolutionA determinant is chosen at random from the set of all determinant of order 2 with elements 0 or 1 only. Find the probability that the determinant chosen is nonzero.
View SolutionA fair coin is tossed 100 times. The probability of getting tails an odd number of times is `1//2` b. `1//8` c. `3//8` d. none of these
View SolutionThe probability that at least one of `Aa n dB` occurs is 0.6. If `Aa n dB` occur simultaneously with probability 0.3, then find the value of `P(A^(prime))+P(B^(prime))dot`
View SolutionAn unbiased die with faced marked 1, 2, 3, 4, 5, and 6 is rolled four times. Out of four face value obtained, the probability that the minimum face value is not less than 2 and the maximum face value is not greater than five is then `16//81` b. `1//81` c. `80//81` d. `65//81`
View SolutionLet A and B be two events such that `P(A)=0.3` and `P(AuuB)= 0.8`. If A and B are independent events, then `P(B)=`
View SolutionA pair of unbiased dice are rolled together till a sum of either 5 or 7 is obtained. Then find the probability that 5 comes before 7.
View SolutionE and F are two independent events. The probability that both e and F happen is 1/12 and the probability that neither E nor F happens is 1/2. Then
View SolutionA man is known to speak the truth 3 out of 4 times. He throws a dice and reports that it is a six. Find the probability that it is actually a six.
View SolutionIf A is an independent event it self then `P(A)=`
View SolutionIf three distinct number are chosen randomly from the first 100 natural numbers, then the probability that all three of them are divisible by both 2 and 3 is `4//25` b. `4//35` c. `4//33` d. `4//1155`
View SolutionOne ticket is selected at random from 100 tickets numbered 00,01,02,...,98,99. If `x_1, a n dx_2` denotes the sum and product of the digits on the tickets, then `P(x_1=9//x_2=0)` is equal to `2//19` b. `19//100` c. `1//50` d. none of these
View SolutionIf three six-faced fair dice are thrown together, the probability that the sum of the numbers appearing on the dice is 16 is
View SolutionFour persons are selected at random out of 3 men, 2 women and 4 children. The probability that there are exactly 2 children in the selection is a. 11/21 b. 9/21 c. 10/21 d. none of these
View SolutionA die is thrown. Let A be the event that the number obtained is greater than 3. Let B be the event that the number obtained is less than 5. Then `P""(AuuB)` is (1) `3/5` (2) 0 (3) 1 (4) `2/5`
View SolutionIf A and B are two events, the probability that exactly one of them occurs is given by
View SolutionIf A and B are two events such that P(A) `gt` 0 and P(B) `lt` 1, then P(`A|barB`) is equal to
View SolutionFor a biased die, the probabilities for the different faces to turn up are given by the table

The die is thrown and you are told that either the face 1 or the face 2 has turned up, then the probability that it is face 1, is
View SolutionA six-faced dice is so biased that it is twice as likely to show an even number as an odd number when thrown. It is thrown twice, the probability that the sum of two numbers thrown is even is `1//12` b. `1//6` c. `1//3` d. `5//9`
View SolutionIn shuffling a pack of 52 playing cards, four are accidently dropped; find the chance that the missing cards should be one from each suit.
View SolutionThe probability that a man who is 85 years old will die before attaining the age of 90 is 1/3. Four persons `A_1,A_2,A_3` and `A_4` are 85 years old. The probability that `A_1` will die before attaining the age of 90 and will be the first to die is
View SolutionThree persons A, B and C speak at a function along with 5 other persons. If the persons speak at random, find the probability that A speaks before B and B speaks before C
View SolutionThe probability that a man will live 10 more years is `1//4` and the probability that his wife will live 10 more years is `1//3`. Then the probability that neither will be alive in 10 years, is
View SolutionTwo number `aa n db` aer chosen at random from the set of first 30 natural numbers. Find the probability that `a^2-b^2` is divisible by 3.
View SolutionIf m is a natural such that m `le` 5, then the probability that the quadratic equation `x^2+mx+1/2+m/2 =0` has real roots is
View SolutionIf two events `A` and `B` such that `P(A')=0.3`, `P(B)=0.5` and `P(AnnB)=0.3`, then `P(B//AuuB')` is
View Solution7 white balls and 3 black balls are kept randomly in order. Find the probability that no two adjacent balls are black.
View SolutionIf from each of the three boxes containing 3 white and 1 black, 2 white and 2 black, 1 white and 3 black balls, one ball is drawn at random, then the probability that 2 white and 1 black balls will be drawn, is
View SolutionThere are four machines and it is known that eactly two of them are faulty. They are tested, one by one, in a random order till both the faulty machines are identified. The probability that only two tests are needed is (A) `1/6` (B) `1/3` (C) `1/2` (D) `1/4`
View SolutionIf E and F are two events such that 0 `lt` P(F)`lt` 1, then
View SolutionThe probability that an event A happens in one trial of an experiment, is 0.4 There independent trials of the experiments are performed. The probability that the event A happens atleast once, is
View SolutionFifteen coupens are numbered `1,2,3,...15` respectively. Seven coupons are selected at random one at a time with replacement The Probability that the largest number appearing on a selected coupon is 9 is :
View SolutionIf A and B toss 3 coins each, The probability that both get equal number of heads is
View SolutionThe probability that a student is not a swimmer is `1/5`. What is the probability that out of 5 students, 4 are swimmers?
View SolutionOne hundred identical coins, each with probability 'p' of showing heads are tossed once. If `0 lt p lt 1` and the probability of heads showing on 50 coins is equal to that of heads showing on 51 coins, then the value of p is
View SolutionNumber of times a fair coin must be tossed so that the probabaility of getting at least one head is at least 0.95 is
View SolutionA box contains N coins, m of which are fair and the rest are biased. The probability of getting a head when a fair coin is tossed is 1/2 while it is 2/3 when a biased coin is tossed. A coin is drawn from the box at random and is tossed twice. The first time it shows head and the second time it shows tail. What is the probability that the coin drawn is fair?
View SolutionThe probability of India winning a test match against West Indies is 1/2. Assuming independence from match to match, find the probability that in a match series Indias second win occurs at the third test.
View SolutionIf ` 0 lt P(A) lt 1, 0 lt P(B) lt 1` and `P(A cup B)=P(A)+P(B)-P(A)P(B)`, then
View SolutionIf `A_1, A_2, …, A_n` are n independent events, such that `P(A_i)=(1)/(i+1), i=1, 2,…, n` , then the probability that none of `A_1, A_2, …, A_n` occur, is
View SolutionA four digit number (numbered from 0000 to 9999) is said to be lucky if sum of its first two digits is equal to the sum of its last two digits. If a four digit number is picked up at random then the probability that it is lucky number is :-
View SolutionThree numbers are chosen at random without replacement from {1,2,3,....10}. The probability that the minimum of the chosen number is 3 or their maximum is 7 , is:
View SolutionOne ticket is selected at random from 50 tickets numbered 00, 01, 02, ... , 49. Then the probability that the sum of the digits on the selected ticket is 8, given that the product of these digits is zero, equals (1) 1/14 (2) 1/7 (3) 5/14 (4) 1/50
View SolutionAn urn contains nine balls of which three are red, four are blue and two are green. Three balls are drawn at random without replacement from the urn. The probability that the three balls have different colour, is
View SolutionLet `omega` be a complex cube root unity with `omega!=1.` A fair die is thrown three times. If `r_1, r_2a n dr_3` are the numbers obtained on the die, then the probability that `omega^(r1)+omega^(r2)+omega^(r3)=0` is `1//18` b. `1//9` c. `2//9` d. `1//36`
View SolutionA signal which can be green or red with probability `4/5 and 1/5` respectively, is received by station A and then and 3 transmitted to station B. The probability of each station receiving the signal correctly is `3/4` If the signal received at station B is green, then the probability that the original signal was green is (a) `3/5` (b) `6/7` (d) `20/23` (d) `9/20`
View SolutionThree numbers are chosen at random from the numbers 1, 2. ... 20. The probability that the arithmetic mean of these numbers is 4 is
View SolutionAn unbiased cubical die is thrown 5 times. The probability that the maximum number appearing on the die is 4 is
View SolutionLet A and B be two events such that P(A) = 3/7, P(B) = 4/7 and P(A`uu`B) = 5/7, Then `(P(A|B))/(P(A'|B))` equals
View SolutionIf A,B and C are three independent events such that
P(A)=P(B)=P(C )=p,
then P (atleast two of A,B and C occur)=`3p^(2)-2p^(3)`
View SolutionA and B are two students. Their probabilities of solving a problem correctly are 1/4 and 1/5 respectively. If the probability of their making a common error is 1/40, and they obtain the same answer, then the probability of their answer is correct is
View SolutionSuppose A and B are two events such that P(A) `ne` 0, P(B) `ne` 0, then
View SolutionFig. 24.8 shows three events A, B and C. Probabilities of different events are shown in the figure. For instance,
`P(A nn B' nn C')`=0.18 , `P(A' nn B nn C')`= 0.06 etc.
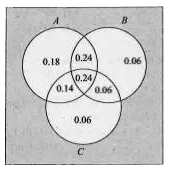
Which of the following is not true ?
View SolutionA fair die is tossed repeated until a six is obtained. Let X denote the number of tosses required.
The probability that `X ge 3` is
View Solutionif `P(A)=0.4,P(B^('))=0.6` and `P(AcapB)=0.15` then the value of `P(A|A^(')cupB^('))` is K. The value of 17 K is equal to.
View SolutionConsider 5 independent Bernoulli.s trials each with probability of success p. If the probability of at least one failure is greater than or equal to `(31)/(32)` , then p lies in the interval : (1) `(1/2,3/4]` (2) `(3/4,(11)/(12)]` (3) `[0,1/2]` (4) `((11)/(12),1]`
View SolutionIf C and D are two events such that `C subD`and P(D) is not equal to 0,` then the correct statement among the following is
View SolutionThree numbers are chosen at random without replacement from {1, 2, 3, ...... 8}. The probability that their minimum is 3, given that their maximum is 6, is (1) `3/8` (2) `1/5` (3) `1/4` (4) `2/5`
View SolutionTen unbiased coins are thrown simultaneously. The probability of getting at least seven heads is
View SolutionOut of 13 applicants for a job, there are 5 women and 8 men. It is desired to select 2 persons for the job. The probability that at least one of the selected persons will be a woman is
View SolutionFour persons A, B, C, D are to speak at a function along with 6 others. If they all speak in random order, the probability that A speaks before B, B before C, C before D is
View SolutionLet A, B, C be pariwise independent events with `P(C) >0 and P(AnnBnnC) = 0`. Then `P((A^c nn B^c)/C)`.
View SolutionFour fair dice `D_(1),D_(2),D_(2) and D_(4)` each having six faces numbered 1, 2, 3, 4, 5 and 6 are rolled simultaneously. The probability that shows a number appearing on one of `D_(1),D_(2) and D_(2)` is:
View SolutionLet A and B be two events such that P(A|B)=1/2 , P(B|A)=1/3, `P(A nn B)`=1/6 , then
View SolutionA ship is fitted with three engines `E_1`, `E_2`, and `E_3`,. The engines function independently of each other with respective probabilities `1/2`. `1/4`and `1/4` ,and For the ship to be operational at least two of its engines must function. Let X denote the event that the ship is operational and let `X_1`, `X_2`, and `X_3` denote respectively the events that the engines `E_1`, `E_2` and `E_3`,are functioning. Which of the following is (are) true?
View Solution
Solved Examples (Level 1 Single Correct ) questions and complete solutions for chapter PROBABILITY of MCGROW HILL EDUCATION MATHS (HINGLISH) of Class 12
All Exercises from MCGROW HILL PUBLICATION Class 12 MATHS PROBABILITY
- Exercises (Level 1 Single Correct Answer)
- Exercises (Level 2 Single Correct Answer)
- Exercises (Numerical Answer)
- Exercises (Single Correct Answer)
- Previous Years AIEEE/JEE Main Papers
- Previous Years B-Architecture Entrance Examination Papers
- Solved Examples (Level 1 Single Correct )
- Solved Examples (Level 2 straight Objective Correct )
- Solved Examples (Numerical Answer )
- Solved Examples (Single Correct )