Complete Solutions to Previous Years B-Architecture Entrance Examination Papers of chapter PROBABILITY of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | PROBABILITY |
| MCGROW HILL PUBLICATION | Previous Years B-Architecture Entrance Examination Papers |
| Number Of Questions | 21 |
| Academic Year | 2023-24 |
Two events A and B are such that P(B) = 0.55 and P(AB') = 0.15. The probability of occurrence of at least one of event is
View SolutionA certain water-supply system consists of a source, three pumping stations, and a destination. Each pump ing station has a probability p (0 `lt` p `lt` 1) of being operable at a specified time to and station functions independently of one another. The stations are connected as shown in figure:
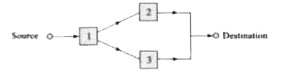
The probability that water is available to the destination at time to is
View SolutionAn urn contains four balls bearing numbers 1, 2, 3 and 123 respectively. A ball is drawn at random from the urn. Let `E_i`, i = 1, 2, 3 donote the event that digit i appears on the ball drawn.
Statement -1: `P(E_1 nn E_2) =P(E_1 nn E_3) = P (E_2 nn E_3)=1/4`
Statement-2: `P(E_1)=P(E_2)=P(E_3)=1/2`
View SolutionThree dice, red, blue and green in colour are rolled together. Let B be the event that sum of the numbers shown up is 7. Let A be the event that the red die shows 1. The conditional probability of the event A given B, P(A|B) is
View SolutionSets A,B,C `AnnB,AnnC,BnnC` and `AnnBnnC` have 35, 40, 45, 13, 12, 14 and 5 elements respectively. An element is selected at random from the set A`uu`B`uu`C. The probability that the selected element belongs to only set A is
View SolutionA man is known to speak the truth 3 out of 4 times. He throws a dice and reports that it is a six. Find the probability that it is actually a six.
View Solutionif `P(A)=0.4,P(B^('))=0.6` and `P(AcapB)=0.15` then the value of `P(A|A^(')cupB^('))` is K. The value of 17 K is equal to.
View SolutionA class consists of 80 students, 25 of them are girls and 55 are boys. If 10 of them are rich and the remaining are poor and also 20 of them are intelligent, then the probability of selecting an intelligent rich girls is `5//128` b. `25//128` c. `5//512` d. none of these
View SolutionLet `Aa n dB` be two event such that `P(AuuB)geq3//4` and `1//8lt=P(AnnB)lt=3//8.` Statement 1: `P(A)+P(B)geq7//8.` Statement 2:`P(A)+P(B)lt=11//8.`
View SolutionA biased coin with probability p, `0ltplt1` of heads is tossed until a head appears for the first time. If the probability that the number of tosses required is even is 2/5, then p equals
View SolutionIf `pa n dq` are chosen randomly from the set `{1,2,3,4,5,6,7,8,9, 10}` with replacement, determine the probability that the roots of the equation `x^2+p x+q=0` are real.
View SolutionIn a binomial distribution `B(n , p=1/4)` , if the probability of at least one success is greater than or equal to `9/(10)` , then n is greater than (1) `1/((log)_(10)^4-(log)_(10)^3)` (2) `1/((log)_(10)^4+(log)_(10)^3)` (3) `9/((log)_(10)^4-(log)_(10)^3)` (4) `4/((log)_(10)^4-(log)_(10)^3)`
View SolutionA box contains 4 white and 5 black balls. A ball is drawn at random and its colour is noted. A ball is then put back in the box along with two additional balls of its opposite colour. If a ball is drawn again from the box, then the probability that the ball drawn now is black, is
View SolutionIf A and B are two independent events such that P(A) = 3/10 and P(A`uu`B) = 4/5. then P( A `nn`B) is equal to:
View SolutionA bag contains three coins, one of which has head on both sides, another is a biased coin that shows up heads 90% of the time and the third one is an unbiased coin. A coin is taken out from the bag at random and tossed. If it is shows up a head, then the probability that it is the unbiased coin, is:
View SolutionTwo numbers are selected at random (without replacement) from first 7 natural numbers. If X denotes the smaller of the two numbers obtained, find the probability distribution of X. Also, find mean of the distribution.
View SolutionA box contains 6 red balls and 2 black balls. Two balls are drawn at random, from it without replacement. If X denotes the number of red balls drawn then E(X) is equal to:
View SolutionA six-faced dice is so biased that it is twice as likely to show an even number as an odd number when thrown. It is thrown twice, the probability that the sum of two numbers thrown is even is `1//12` b. `1//6` c. `1//3` d. `5//9`
View SolutionIf for two events A and B, in a random experiment, P(A|B) = 4/5 and P(B|A) = 1/4, then P(A | A `uu` B) is equal to _____
View SolutionA bag contains 8 white and 6 black balls. A ball is drawn at random from the bag, its colour is observed and is kept aside (i.e. not returned in the bag). Three additional balls of the same colour as observed are put in the bag. If now two balls are drawn simultaneously at random from the bag, then the probability that these are of different colours, is ____
View SolutionIndia plays two matches each with West Indies and Australia. In any match the probabilities of India getting points `0, 1 and 2` are `0.45, 0.05 and 0.50` respectively. Assuming that the outcomes are independent, the probability of India getting at least 7 points is (a) `0.8750` (b) `0.0875` (c) `0.0625` (d) `0.0250`
View Solution
Previous Years B-Architecture Entrance Examination Papers questions and complete solutions for chapter PROBABILITY of MCGROW HILL EDUCATION MATHS (HINGLISH) of Class 12
All Exercises from MCGROW HILL PUBLICATION Class 12 MATHS PROBABILITY
- Exercises (Level 1 Single Correct Answer)
- Exercises (Level 2 Single Correct Answer)
- Exercises (Numerical Answer)
- Exercises (Single Correct Answer)
- Previous Years AIEEE/JEE Main Papers
- Previous Years B-Architecture Entrance Examination Papers
- Solved Examples (Level 1 Single Correct )
- Solved Examples (Level 2 straight Objective Correct )
- Solved Examples (Numerical Answer )
- Solved Examples (Single Correct )