Complete Solutions to PAPER 2( MATHEMATICS) of chapter PRACTICE SET 07 of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | PRACTICE SET 07 |
| MHTCET PRACTICE PAPER | PAPER 2( MATHEMATICS) |
| Number Of Questions | 50 |
| Academic Year | 2023-24 |
If ` -5,k and -1` are in AP, then the value of k is equal to
00:48View SolutionWhich term of the series `sqrt2,2/3,(2sqrt2)/9,.....` is `16/2187`?
02:24View SolutionIf a striaght line passes through the points (`-1/2,1)` and (1,2) then its x-intercept is
02:05View SolutionThe slopes of the lines which make an angle `45^@` with the line `3x-y=-5` is
02:34View SolutionThe length of the latusrectum of the ellipse `16x^(2)+25y^(2)=400` is
02:02View SolutionThe derivative of `sin^(-1)((2x)/(1+x^(2)))` with respect to `cos^(-1)((1-x^(2))/(1+x^(2)))` is
03:12View SolutionIf the function `y= sin^(-1)x, "then" (1-x^(2))(d^(2)y)/(dx^(2))` is equal to
04:00View SolutionThe function `f(x)=e^(-|x|)` is
03:24View SolutionIf X is a binomial variate with the range `{0, 1, 2, 3, 4, 5, 6}` and `P(X= 2) = 4P(X = 4)` , then the parameter p of X is
03:09View SolutionFind the area bounded by the curves `x^2+y^2=25 ,4y=|4-x^2|,` and `x=0` above the x-axis.
04:48View Solution`int{log(logx)+(1)/((logx)^(2))}dx=x {f (x)-g(x)}+C`, then
05:21View Solution`int(1+tan^2x)/(1-tan^2x)dx`
01:32View SolutionThe area (in sq unit) of the triangle formed by `x+y+1=0` and the pair of straight lines `x^2-3xy+2y^2=0` is
03:42View SolutionThe equation `y^(2)-x^(2)+2x-1=0`, represents
02:17View SolutionThe value of the integral `int f_(0)^(2)|x^(2)-1|dx` is
01:38View SolutionIf `AB=I and B=A'`, then
01:31View SolutionIf the system of equations `2x-3y+5z=12, 3x+y+lambdaz= mux7+y+8z=17` has infinitely many real solutions, then `lambda+mu`=
04:06View SolutionThe differential equation of all parabolas whose axis are parallel to the y-axis is (a) `( b ) (c) (d)(( e ) (f) d^(( g )3( h ))( i ) y)/( j )(( k ) d (l) x^(( m )3( n ))( o ))( p ) (q)=0( r )` (s) (b) `( t ) (u) (v)(( w ) (x) d^(( y )2( z ))( a a ) x)/( b b )(( c c ) d (dd) y^(( e e )2( f f ))( g g ))( h h ) (ii)=C (jj)` (kk) (c) `( d ) (e) (f)(( g ) (h) d^(( i )3( j ))( k ) y)/( l )(( m ) d (n) x^(( o )3( p ))( q ))( r ) (s)+( t )(( u ) (v) d^(( w )2( x ))( y ) x)/( z )(( a a ) d (bb) y^(( c c )2( d d ))( e e ))( f f ) (gg)=0( h h )` (ii) (d) `( j j ) (kk) (ll)(( m m ) (nn) d^(( o o )2( p p ))( q q ) y)/( r r )(( s s ) d (tt) x^(( u u )2( v v ))( w w ))( x x ) (yy)+2( z z )(( a a a ) dy)/( b b b )(( c c c ) dx)( d d d ) (eee)=C (fff)` (ggg)
01:48View SolutionIf `(x^2+y^2)dy=xydx` and y(1)=1 and `y(x_o)=e`, then `x_o=`
04:22View SolutionThe integrating factor of `x(dy)/(dx)+(1+x)y=x `is
03:08View Solutionif `0<=x<=pi` and `81^(sin^2x)+81^(cos^2x)=30` then `x=`
02:54View SolutionIn `Delta ABC ` , a= 6 ,b=3 and cos (A-B) = 4/5 .Then are of triangle is
03:03View SolutionFind the equation of a normal to the curve `y = x log_e x` which is parallel to the line `2x - 2y + 3 = 0.`
03:13View SolutionArea common to the circle `x^(2)+y^(2)=9` an the parbola `y^(2)=8x` is
04:56View SolutionIf three points A, B and C have position vectors `hati + x hatj + 3 hatk, 3 hati + 4 hatj + 7 hatk and y hati -2hatj - 5 hatk ` respectively are collinear, then (x, y) =
02:35View SolutionIf a,b,c are mutually perpendicular unit vectors then `|a+b+c|`=
01:38View SolutionIn a Boolean Algebra `pvvp` is equl to
00:40View SolutionIf P be the point `(2,6, 3)` then the equation of the plane through P, at right angles to OP, where 'O' is the origin is
03:06View Solutionसिद्ध कीजिए की `f(x)=tan ^(-1)(sin x + cos x ),x gt 0 ` से प्रदत फलन `f,(0,pi/4)` में निरंतर वर्धमान फलन है |
03:33View Solutionthe equation of the circle passing through the foci of the ellipse `(x^(2))/(16)+(y^(2))/(9)=1` and having centre at (0,3) is
05:00View SolutionEquation of tangent to the parabola `y^(2)=16x` at P(3,6) is
03:43View SolutionIf `cos(A-B) = 3/5, tan A*tan B = 2` which of the following is true
01:53View SolutionFind the equation of a circle with centre ` (h, k)` and touching the x -axis.
01:43View SolutionAngle between tangents drawn to circle `x^2+y^2=20` from the point `(6, 2)` is
03:24View SolutionThe valume of the parallelopiped whose coterminous edges are `hati-hatj+hatk,2hati-4hatj+5hatk and 3hati-5hatj+2hatk`, is
04:17View SolutionConsider the inequalities `x_(1)+x_(2) le,2, 2x_(1)+5x_(2) ge 10, x_(1),x_(2) ge0`. Which of the following point lie in the fesible region ?
02:08View SolutionThe switching function for the following network is
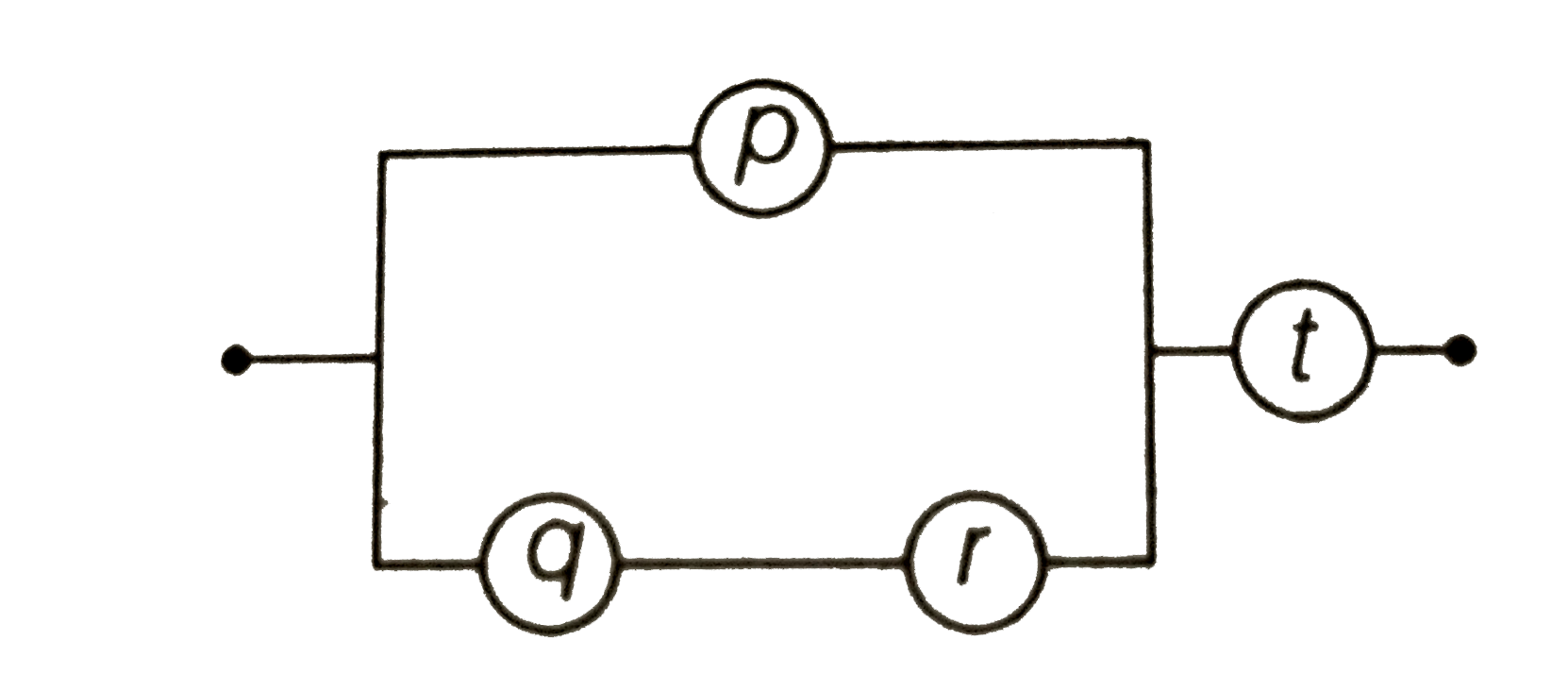 02:54View Solution
02:54View SolutionGien that X is discrete random variable which take the values, `0,1,2 and P(X=0)=(144)/(169),P(X=1)=(1)/(169)`, then the value of `P(X=2)` is
01:23View SolutionThe degree of the differential equation `(d^(3)y)/(dx^(3))+2 "sin"(dy)/(dx)+y=0` is
01:43View Solutionif `x=a cos^(4) theta, y= a sin^(4) theta, "then" (dy)/(dx)"at" theta=(3pi)/(4)` is
04:14View SolutionFor any square matrix `A,A A^(T)` is a
01:49View SolutionIf the pair of straight lines `xy - x - y +1=0` & the line `ax+2y-3=0` are concurrent then `a =`
02:32View SolutionIf `y=sqrt(x s inx+sqrt(sinx+sqrt(sinx+ tooo))),p rov et h a t(dy)/(dx)=(cosx)/(2y-1)`
03:20View SolutionThe differential equation, obtained on eliminating A and B from the equations `y= A cos omega wt+ B sin omega t` is
04:17View SolutionThe equation `sin^-1x-cos^-1x=cos^-1(sqrt3/2)` has
05:07View Solution`lim_(x->0) (tan x - sin x)/(x^3)` is equal to
01:53View SolutionIf `2 cos x ne 2 sin, x` then the general solution of `sin^(2)x-cos2x=2 sin 2x` is
02:07View SolutionThe equation of the plane passing through the points (1,2,3), (-1,4,2) and (3,1,1) is
06:36View SolutionThe eqution of the plane which meets the axes in A,B,C such that the centroid of the `Delta BAC is ((1)/(3)(1)/(3),(1)/(3))` is given by
01:14View SolutionIf `a=hati-hatj-hatk and b= lambda hati-3hatj+ hatk` and the orthogonal projection of b on a is `(4)/(3) (hati-hatj-hatk)` then `lambda` is equal to
05:03View Solution
PAPER 2( MATHEMATICS) questions and complete solutions for chapter PRACTICE SET 07 of MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS of Class 12
