Complete Solutions to EXERCISE 2 of chapter OSCILLATIONS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | OSCILLATIONS |
| MHTCET PREP GUIDE | EXERCISE 2 |
| Number Of Questions | 49 |
| Academic Year | 2023-24 |
A body of mass 0.01 kg executes simple harmonic motion about x = 0 under the influence of a force shown in the figure. The period of the SHM is

View SolutionPeriod if small oscillations in the two cases shown in the figure is `T_(1) and T_(2)`, respectively then

View SolutionThe variation of PE of harmonic oscillator is as shown in the figure. The spring constant is

View SolutionA particle is in linear SHM of amplitude A and time period T. If v refers to its average speed during any interval of T/3 , then the maximum possible value of v is
View SolutionMaximum kinetic energy of a particle of mass 1 kg in SHM is 8 J. Time period of SHM is 4 s. Maximum potential energy during the motion is 10 J. Then
View SolutionTwo particles execute simple harmonic motion of same amplitude and frequency along the same straight line. They pass on another, when going in opposite directions, each time their displacement is half of their amplitude. What is the phase difference between them?
View SolutionA particle under the action of a force has a period of `3s` and under the action of another force it has a period `4sec` in `SHM`. What will be its period under the combined action of both forces in the same direction?
View SolutionA body is executing simple harmonic motion. At a displacement `x` its potential energy is `E_(1)` and at a displacement `y` its potential energy is `E_(2)` The potential energy `E` at displacement `(x+y)` is
View SolutionA horizontal platform with an object placed on it is executing SHM in the vertical direction . The amplitude of oscillation is `4 xx 10^(-3)` m. What must be least period of these oscillations , so that the object is not detached from the platform ? (take , `g=10 ms^(-2)`)
View SolutionA 10 kg metal block is attached to a spring constant `1000 Nm^(-1)`. A block is displaced from equilibrium position by 10 cm and released. The maximum acceleration of the block is
View SolutionThe potential energy of a particle of mass 2 kg in SHM is `(9x^(2))`J. Here x is the displacement from mean position . If total mechanical energy of the particle is 36 J. The maximum speed of the particle is
View SolutionWhen a particle executes SHM oscillates with a frequency v, then the kinetic energy of the particle
View SolutionTwo identical springs `S_(1) and S_(2)` are joined as shown in the figure. The oscillation frequency of the m is v. What will be the frequency of mass m, if one spring is removed ?

View SolutionA particle moves with simple harmonic motion in a straight line. In first `taus`, after starting form rest it travels a destance a, and in next `tau s` it travels 2a, in same direction, then:
View SolutionA solid cube floats in water half immersed and h small vertical oscillations of time period `pi/5`s. Find the mass (in kg) Take g=10m/`s^(2)`.
View Solutionwhen two displacements represented by `y_(1) = a sin(omega t)` and `y_(2) = b cos (omega t)` are superimposed the motion is
View SolutionA simple pendulum has time period `T_(1)`/ The point of suspension is now moved upward according to the realtion `y = kt^(2)(k = 1 m//s^(2))` where `y` is vertical displacement, the time period now becomes `T_(2)`. The ratio of `((T_(1))/(T_(2)))^(2)` is : `(g = 10 m//s^(2))`
View SolutionA simple harmonic oscillator consists of a particle of mass m and an ideal spring with spring constant k. The particle oscillates with a time period T. The spring is cut into two equal parts. If one part oscillates with the same particle, the time period will be
View SolutionThe displacement-time graph of a particle executing SHM is shown.
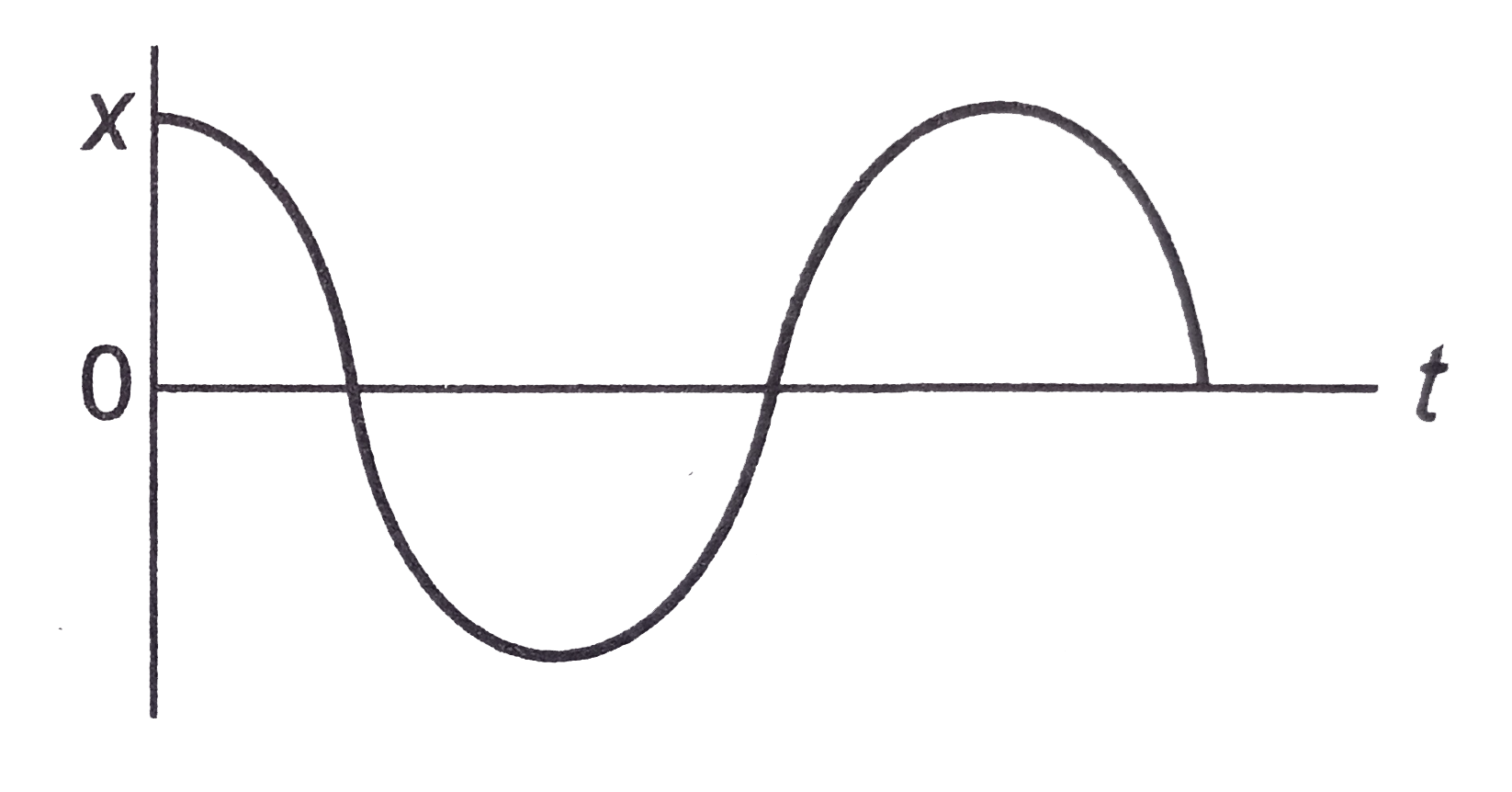
Which of the following statement(s) is/are true ?
I. The force is zero at t = 3T/4
II. The acceleration is maximum at t = T
III. The velocity is maximum at t = T/4
IV. The potential energy is equal to kinetic energy at t = T/2
View SolutionThe period of oscillation of a simple pendulum of length (L) suspended from the roof of a vehicle which moves without friction down an inclined plane of inclination (prop), is given by.
View SolutionA spring balance has a scale that reads `0` to `20kg`. The length of the scale is `10cm`. A body suspended from this balance, when displaced and released, oscillates with period of `(pi)/(10)s`. The mass of the body is
View SolutionA particle is executing SHM along a straight line. Its velocities at distances `x_(1)` and `x_(2)` from the mean position are `v_(1)` and `v_(2)`, respectively. Its time period is
View SolutionA particle executes simple harmonic motion with a period of `16s`. At time `t=2s`, the particle crosses the mean position while at `t=4s`, its velocity is `4ms^-1` amplitude of motion in metre is
View SolutionWhen the potential energy of a particle executing simple harmonic motion is one-fourth of its maximum value during the oscillation, the displacement of the particle from the equilibrium position in terms of its amplitude a is
View SolutionTwo particles A and B execute simple harmonic motions of period T and `5T//4`. They start from mean position. The phase difference between them when the particle A complete an oscillation will be
View SolutionA particle starts oscillating simple harmonically from its equilibrium position then, the ratio of kinetic energy and potential energy of the particle at the time `T//12` is: `(T="time period")`
View SolutionA wooden cube (density of wood `'d'`) of side `'l'` flotes in a liquid of density `'rho'` with its upper and lower surfaces horizonta. If the cube is pushed slightly down and released, it performs simple harmonic motion of period `'T'`. Then, `'T'` is equal to :-
View SolutionThe ration of kinetic energy to the potential energy of a particle executing SHM at a distance equal to half its amplitude , the distance being measured from its equilibrium position is
View SolutionThe dispalcement of an object attached to a spring and excuting simple harmonic motion is given by `x = 2 xx 10^(-2) cospit` metres. The time at which at maximum speed first occurs is :
View SolutionFind the time taken by the particle in going from ` x = (A)/2` to `x=A`
Hint `: t_(1) =` Time taken to go from `x=0` to `x =A `
`t_(2) = ` Time taken to go from `x=0` to`x= (A)/(2)`
Required time `= t_(1) - t_(2)`
View SolutionA mass `M` attached to a horizontal spring executes `SHM` with an amplitude `A_(1)`. When mass `M` passes through its mean position a smaller mass `m` is placed over it and both of them move togther with amplitude `A_(2)`. Ratio of `((A_(1))/(A_(2)))` is:
View SolutionA particle oscillates simple harmonically along a straight line with period 8 seconds and amplitude `8 sqrt(2)`m. It starts from the mean position, then the ratio of the distances travelled by it in the second second and first second of its motion is
View SolutionTwo identical springs are connected to mass m as shown (k = spring constant). If the period of the configuration in (a) is 2s, the period of the configuration in (b) is
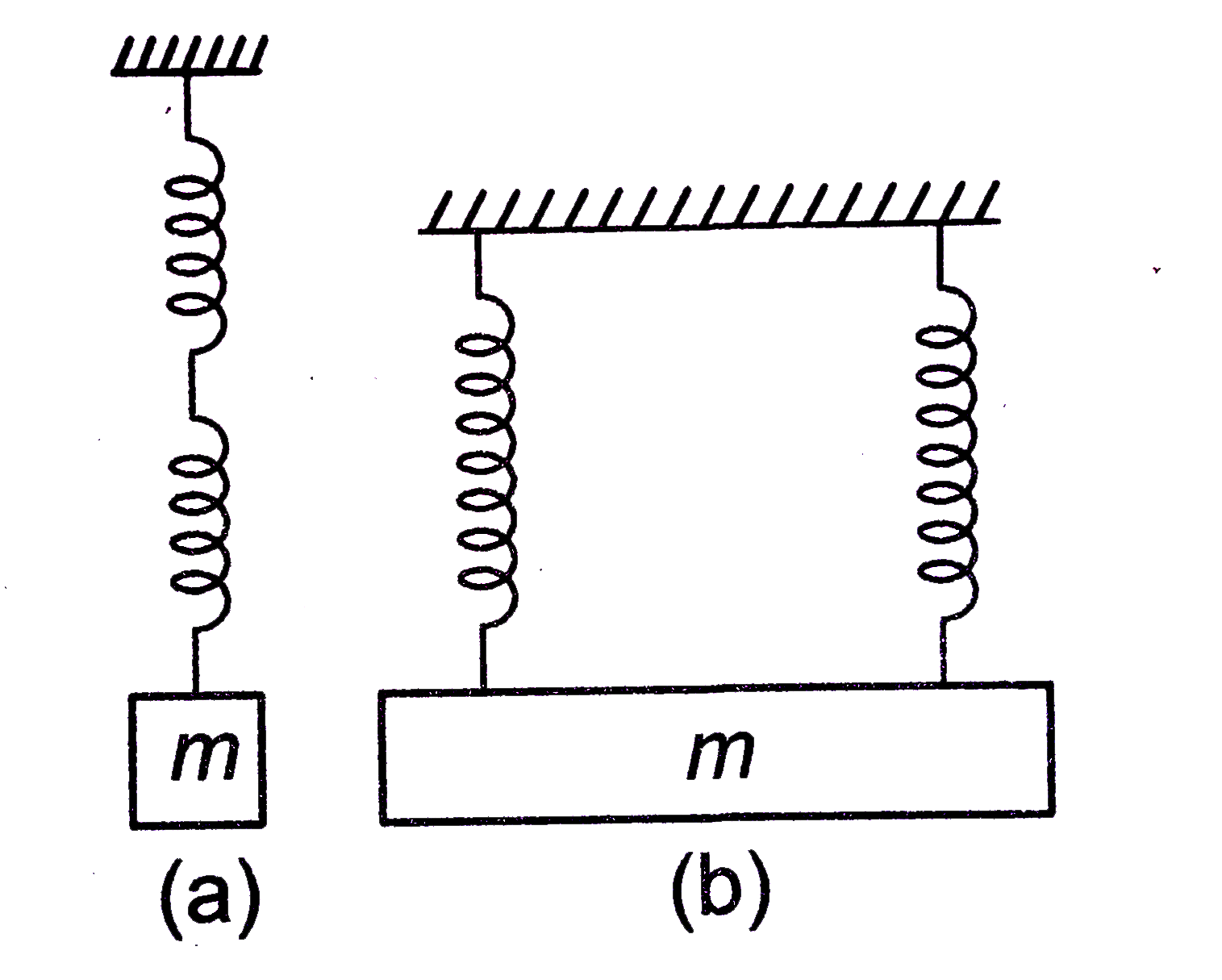
View SolutionThe distance moved by a particle in simple harmonic motion in one time period is
View SolutionTwo pendulums have time period T and 5T/4. They starts SHM at the same time from the mean position. What will be the phase difference between them after the bigger pendulum completed one oscillation ?
View SolutionMaximum velocity ini SHM is `v_(m)`. The average velocity during motion from one extreme point to the other extreme point will be
View SolutionA particle is acted simultaneously by mutally perpendicular simple harmonic motion `x=acosomegat` and `y=asinomegat`. The trajectory of motion of the particle will be
View SolutionThe maximum velocity and maximum acceleration of a particle per for ming a linear SHM are `alpha and beta` respectively. Then path length of the particle is
View SolutionA pendulum with time period of `1s` is losing energy due to damping. At time its energy is `45 J`. If after completing `15` oscillations, its energy has become `15 J`. Its damping constant (in `s^(-1)`) is :-
View SolutionA weakly damped harmonic oscillator of frequency `n_1` is driven by an external periodic force of frequency `n_2`. When the steady state is reached, the frequency of the oscillator will be
View SolutionThe amplitude of a executing `SHM` is `4cm` At the mean position the speed of the particle is `16 cm//s` The distance of the particle from the mean position at which the speed the particle becomes `8 sqrt(3)cm//s` will be
View SolutionThe displacement of a particle is represented by the equation `y=sin^(3)omegat.` The motion is
View SolutionFor a particle performing `SHM`, equation of motion is given as `(d^(2))/(dt^(2)) + 4x = 0`. Find the time period
View SolutionFor a particle executing SHM, x = displacement from mean position, v = velocity and a = acceleration at any instant, then
View SolutionA particle is executing SHM. Then the graph of acceleration as a function of displacement is
View SolutionThe ratio of amplitudes of following SHM is `x_(1) = A sin omega t and x_(2) = A sin omega t + A cos omega t`
View SolutionA man measures time period of a pendulum (T) in stationary lift. If the lift moves upward with acceleration `(g)/(4)`, then new time period will be
View SolutionThe oscillation of a body on a smooth horizontal surface is represented by the equation, `X = A cos (omega t)`
where X = displacement at time t
`omega` = frequency of oscillation
Which one of the following graphs shows correctly the variation a with t ?
View SolutionThe displacement of a linear simple harmonic oscillator is given by `y = "sin"(pi)/(2)[(t)/(2)+(1)/(2)]` cm. The maximum acceleration of the oscillator in `cms^(-2)` is
View Solution
EXERCISE 2 questions and complete solutions for chapter OSCILLATIONS of MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS of Class 12