Complete Solutions to EXERCISE 1 of chapter OSCILLATIONS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | OSCILLATIONS |
| MHTCET PREP GUIDE | EXERCISE 1 |
| Number Of Questions | 67 |
| Academic Year | 2023-24 |
Two bodies (M) and (N) of equal masses are suspended from two separate massless springs of spring constants (k_1) and (k_2) respectively. If the two bodies oscillate vertically such that their maximum velocities are equal, the ratio of the amplitude of vibration of (M) to the of (N) is.
View SolutionA body is executing SHM with an amplitude of 0.1 m. Its velocity while passing through the mean position is `3ms^(-1)`. Its frequency in Hz is
View SolutionTwo particle are executing SHMs .The equations of their motions are `y_(1)=10"sin"(omegat+(pi)/(4)) " and "y_(2)=5 "sin"(omegat+(sqrt(3)pi)/(4))` What is the ratio of their amplitudes.
View SolutionThe maximum speed of a particle executing S.H.M. is 1 m/s and its maximum acceleration is`1.57 m// sec^(2)` . The time period of the particle will be
View SolutionA particle of mass 1 kg is moving in SHM with an amplitude 0.02 m and a frequency of 60 Hz. The maximum force (in N) acting on the particle is
View SolutionA horizontal plank has a rectangular block placed on it. The plank starts oscillating vertically and simple harmonically with an amplitude of 40 cm. The block just loses contact with the plank when the latter is at momentary rest Then.
View SolutionA body has a time period `T_(1)` under the action of one force and `T_(2)` under the action of another force, the square of the time period when both the forces are acting in the same direction is
View SolutionA body of mass 5 gm is executing S.H.M. about a point with amplitude 10 cm . Its maximum velocity is 100 cm / sec . Its velocity will be 50 cm / sec at a distance
View SolutionThis time period of a particle undergoing SHM is 16 s. It starts motion from the mean position. After 2 s, its velocity is 0.4 `ms^(-1)`. The amplitude is
View SolutionThe maximum acceleration of a body moving is SHM is `a_(0)` and maximum velocity is `v_(0)`. The amplitude is given by
View SolutionThe time period of a simple pendulum inside a stationary lift is `sqrt(5)` s. What will be the time period when the lift moves upward with an acceleration `(g)/(4)`?
View SolutionA particle executes simple harmonic motion with an amplitude of 4 cm . At the mean position the velocity of the particle is 10 cm/ s . The distance of the particle from the mean position when its speed becomes 5 cm/s is
View SolutionA block of mass `m` is resting on a piston as shown in figure which is moving vertically with a `SHM` of period `1 s`. The minimum amplitude of motion at which the block and piston separate is :

View SolutionA particle executes SHM, its time period is 16 s. If it passes through the centre of oscillation, then its velocity is 2 `ms^(-1)` at times 2 s. The amplitude will be
View SolutionThe equation of SHM of a particle is given as `2(d^(2)x)/(dt^(2))+32x=0` where x is the displacement from the mean position. The period of its oscillation ( in seconds) is -
View SolutionAn iron ball of mass M is hanged from the ceilling by a spring with a spring constant k. It executes a SHM with a period P. If the mass of the ball is increased by four times, the new period will be
View SolutionThe amplitude of a executing `SHM` is `4cm` At the mean position the speed of the particle is `16 cm//s` The distance of the particle from the mean position at which the speed the particle becomes `8 sqrt(3)cm//s` will be
View SolutionA particle executing simple harmonic motion of amplitude 5 cm has maximum speed of 31.4 cm / s . The frequency of its oscillation is
View SolutionThe maximum velocity a particle, executing simple harmonic motion with an amplitude 7 mm, 4.4 m//s. The period of oscillation is.
View SolutionThe motion of a particle is given by `x=A sin omegat+Bcos omegat`. The motion of the particle is
View SolutionThe amplitude and maximum velocity will be respectively `X= 3 sin 2t + 4 cos 2t`The amplitude and maximum velocity will be respectively
View SolutionOut of the following functions representing motion of a particle which represents SHM
I. `y = sin omega t - cos omega t`
II. `y = sin^(3)omega t`
III. `y = 5 cos ((3 pi)/(4)-3 omega t)`
IV. `y = 1 + omega t + omega^(2)t^(2)`
View SolutionThe displacement of a particle from its mean position (in mean is given by `y = 0.2 sin(10pi t + 1.5 pi) cos (10 pi t+ 1.5 pi)`. The motion but not `S.H.M.`
View SolutionWhich of the following functionss represents a simple harmonic oscillation ?
View SolutionThe displacement of two particles executing SHM are represented by equations, `y_(1)=2 sin (10 t + theta), y_(2)=3 cos 10 t`. The phase difference between the velocity of these particles is
View SolutionTwo pendulums of length 1.21 m and 1.0 m starts vibrationg. At some instant, the two are in the mean position in same phase. After how many vibrations of the longer pendulum, the two will be in phase ?
View SolutionTwo SHMs are respectively represented by `y_(1)=a sin (omegat-kx) and y_(2)=b cos(omegat-kx)`. The phase difference between the two is
View SolutionThe displacement-time graph of a particle executing SHM is shown in the figure. Which of the following statements is false ?
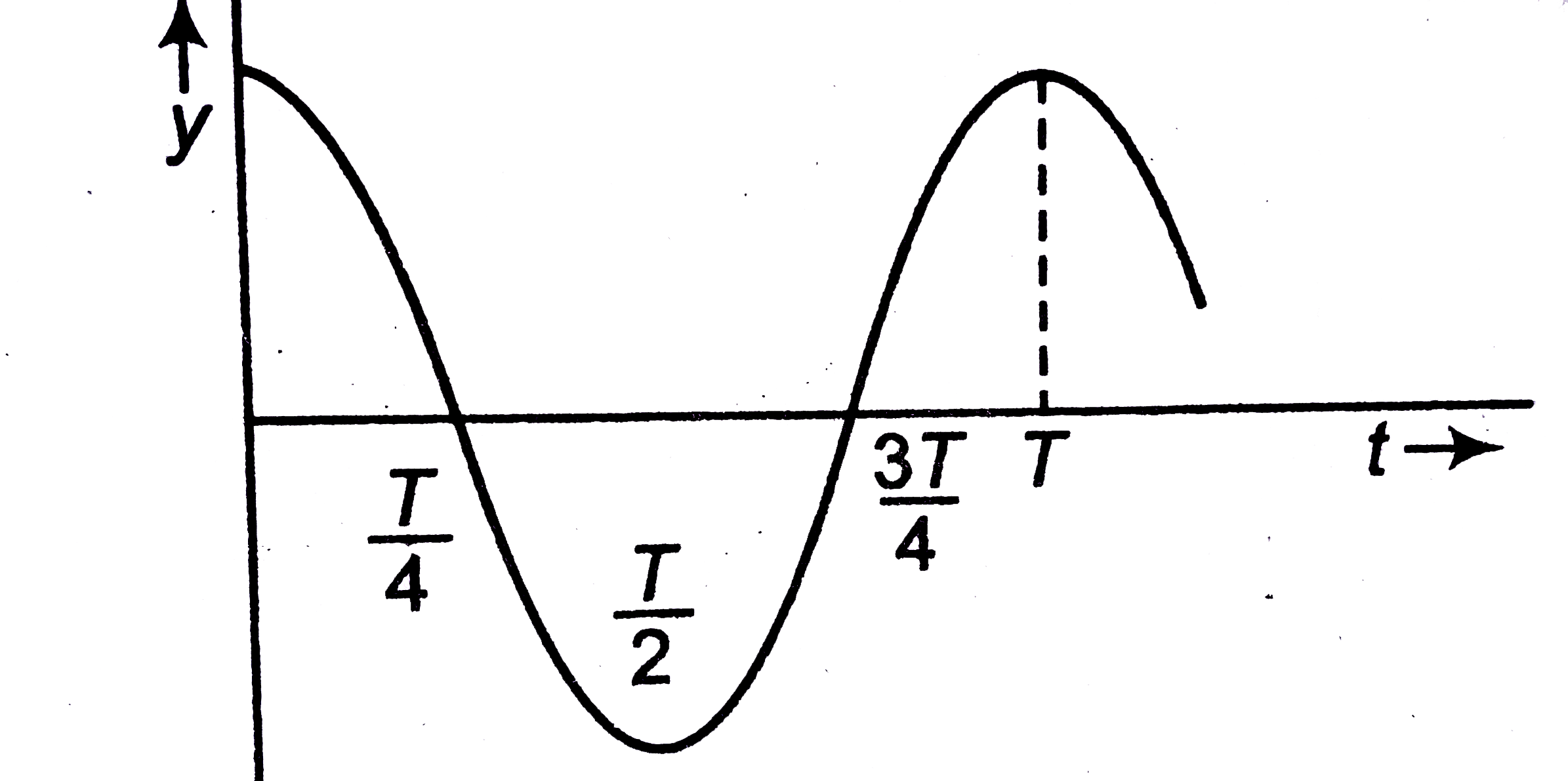
View SolutionThe displacement-time graph of a particle executing SHM is as shown in the figure.

The corresponding force-time graph of the particle is
View SolutionThe period of SHM of a particle is 12 s. The phase difference between the positions at t = 3 s and t = 4 s will be
View SolutionTwo simple harmonic motions given by, `x = a sin (omega t+delta)` and `y = a sin (omega t + delta + (pi)/(2))` act on a particle will be
View SolutionThe resultant of two rectangular simple harmonic motion of the same frequency and unequal amplitude but differing in phase by `pi//2` is
View SolutionA particle is executing two different simple harmonic motions, mutually perpendicular, of different amplitudes and having phase difference of `pi//2`. The path of the particle will be
View SolutionThe potential energy of a simple harmonic oscillator when the particle is half way to its end point is
(where, E is the total energy)
View SolutionFor a linear harmonic oscillator, its potential energy, kinetic energy and total energy given by `E_(P), K_(K) and E_(T)` respectively. Its maximum acceleration is given by
View SolutionA point particle if mass `0.1 kg` is executing SHM of amplitude `0.1 m`. When the particle passes through the mean position, its kinetic energy is `8 xx 10^(-3)J`. Write down the equation of motion of this particle when the initial phase of oscillation is `45^(@)`.
View SolutionWhen the potential energy of a particle executing simple harmonic motion is one-fourth of its maximum value during the oscillation, the displacement of the particle from the equilibrium position in terms of its amplitude a is
View SolutionFor a particle executing SHM the displacement x is given by `x = A cos omega t`. Identify the graph which represents the variation of potential energy (PE) as a function of time and displacement x.
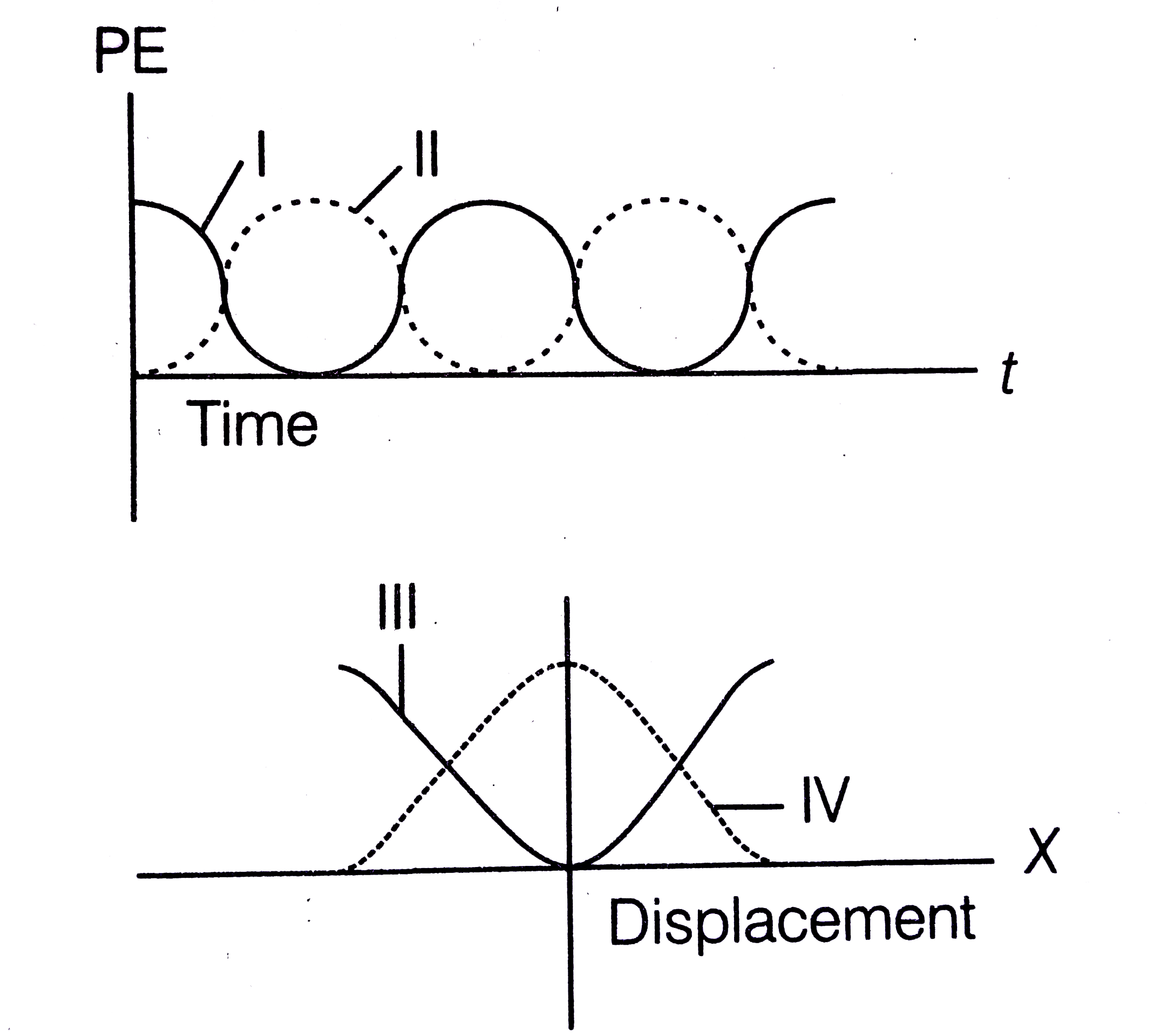
View SolutionThe force constant of a weightless spring is `16 N m^(-1)`. A body of mass `1.0 kg` suspended from it is pulled down through `5 cm` and then released. The maximum energy of the system (spring + body) will be
View SolutionThe total energy of the body executing SHM is E. the, the kinetic energy when the displacement is half of the amplitude is
View SolutionIf the KE of a particle performing a SHM of amplitude A is `(3)/(4)` of its total energy, then the value of its displacement is
View SolutionConsider the following statements. The total energy of a particle executing simple harmonic motion depends on its
(1) Amplitude
(2) Period
(3) Displacement Of these statements
View SolutionThe amplitude of a particle executing SHM is made three-fourth keeping its time period constant. Its total energy will be
View SolutionA particle of mass `m` oscillates with simple harmonic motion between points `x_(1)` and `x_(2)` the equilibrium position being `O` its potential energy in plotted it will be as given bellow in the graph
View SolutionA simple pendulum has a length I. The inertial and gravitational masses of the bob are `m_(i) and m_(g)`, respectively. Then, the time period T is given by
View SolutionThe acceleration due to gravity on the moon is `(1)/(6)`th the acceleration due to gravity on the surface of the earth. If the length of a second's pendulum is 1 m on the surface of the earth, then its length on the surface of the moon will be
View SolutionA simple pendulum of length L and mass (bob) M is oscillating in a plane about a vertical line between angular limit `-phi` and `+phi`. For an angular displacement `theta(|theta|ltphi)`, the tension in the string and the velocity of the bob are T and V respectively. The following relations hold good under the above conditions:
View SolutionIf the length of second's pendulum is decreased by 2%, how many seconds it will lose per day
View SolutionTwo simple pendulum of length `5m` and `20m` respectively are given small displacement in one direction at the same time. They will again be in the same phase when the pendulum of shorter length has completed oscillation.
View SolutionA and B are fixed points and the mass M is tied by strings at A and B. If the mass M is displaced slightly out of this plane and released, it will execute oscillations with period.
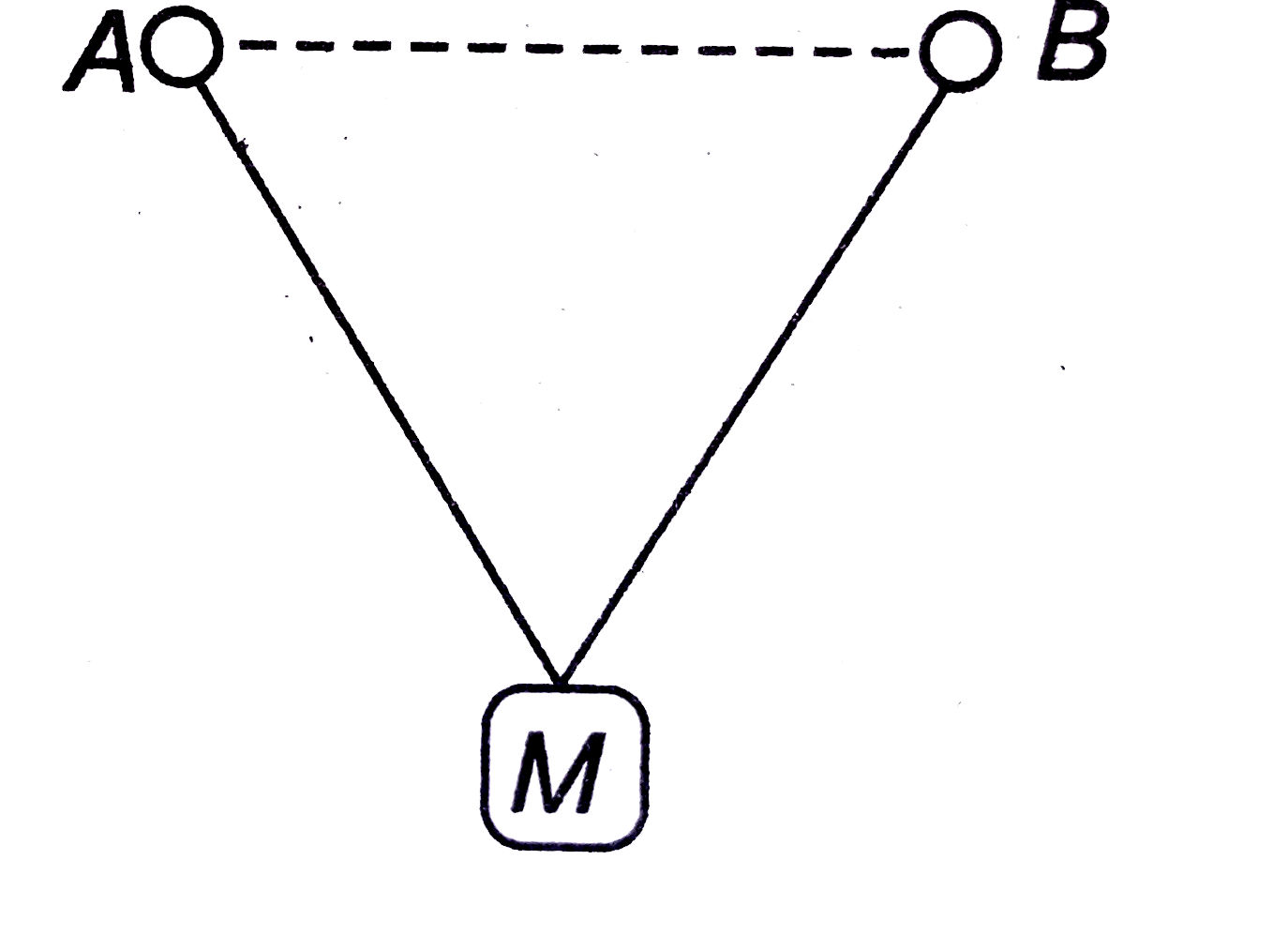
(Given, AM = BM = L, AB = 2d)
View SolutionTwo simple pendulum first of bob mass `M_(1)` and length `L_(1)` second of bob mass `M_(2)` and length `L_(2) M_(1) = M_(2)` and `L_(1)` = 2L_(2)`. if the vibrational energy of both is same which is correct?
View SolutionThe mass and diameter of a planet are twice those of earth. What will be the period of oscillation of a pendulum on this plenet. If it is a 2 second's pendulum on earth?
View SolutionA clock pendulum made of invar has a period of `0.5sec` at `20^(@)C`. If the clock is used in a climate where the temperature average to `30^(@)C`, how much time does the clock loose in each oscilliation. For innar `alpha = 9 xx 10^(-7) ^(@)C^(-1)`
View SolutionThe time period of a simple pendulum in a stationary train is T. The time period of a mass attached to a spring is also T. The train accelerates at the rate 5 `ms^(-2)`. If the new time periods of the pendulum and spring be `T_(p) and T_(s)`, respectively. Then,
View SolutionIn case of a simple pendulum, time period versus length is depicted by
View SolutionA simple spring has length l and force constant K. It is cut into two springs of lengths `l_(1) "and" l_(2)` such that `l_(1) = n l_(2)` (n = an integer). The force constant of spring of length `l_(1)` is
View SolutionA particle of mass 200 g executes a simpel harmonit motion. The resrtoring force is provided by a spring of spring constant `80 N m^-1`. Find the time period.
View SolutionA massless spring, having force constant k, oscillates with frequency n when a mass m is suspended from it. The spring is cut into two equal halves and a mass `2m` is suspended from one half. The frequency of oscillation will now be
View SolutionAn object suspended from a spring exhibits oscillations of period T. Now, the spring is cut in two halves and the same object is suspended with two halves as shown in the figure. The new time period of oscillation will become

View SolutionIf `k_(s) and k_(p)`, respectively are effective spring constants in series and parallel combination of springs as shown in the figure, find `(k_(s))/(k_(p))`
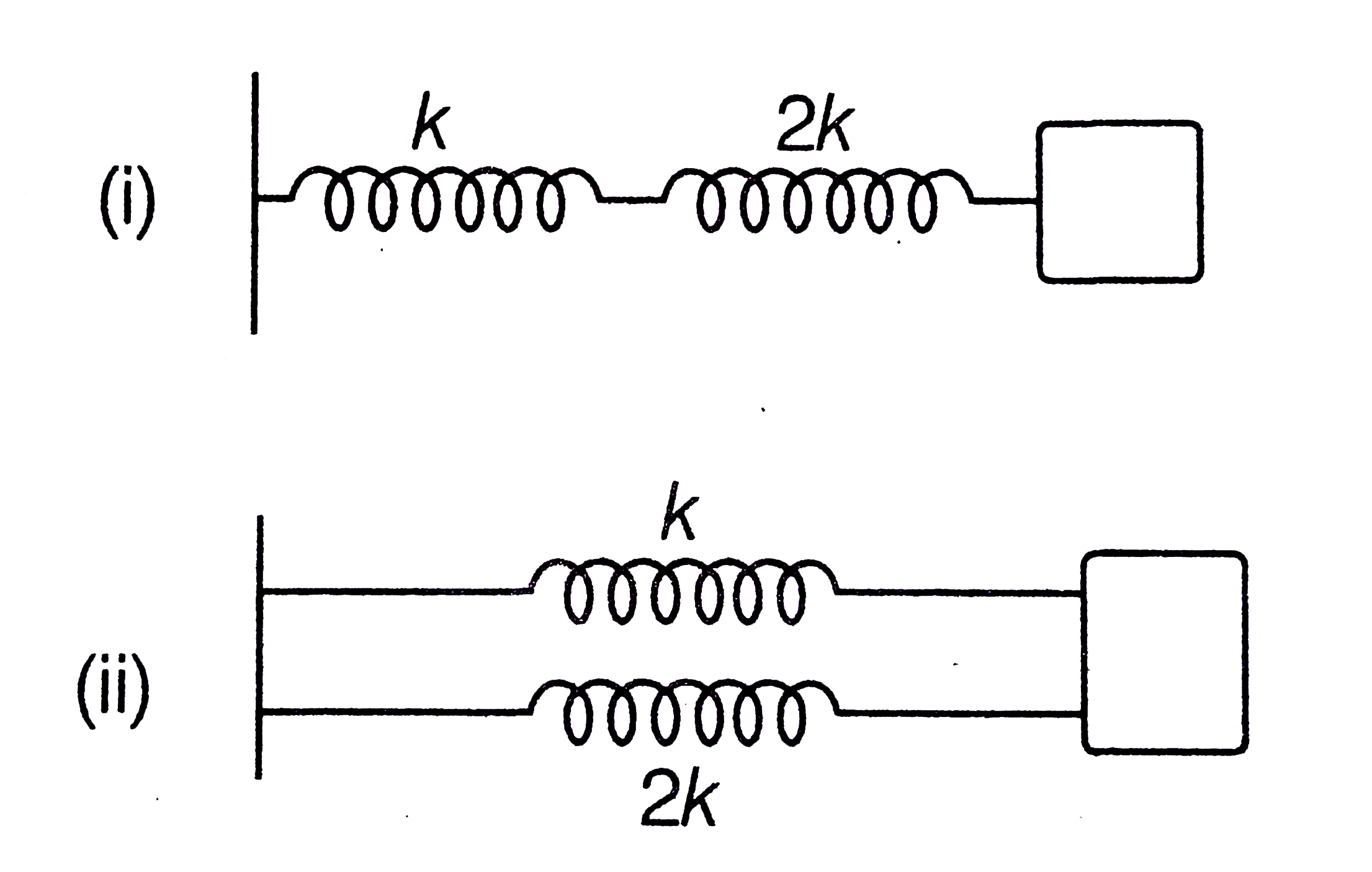
View SolutionIf f is the frequency when mass m is attached to a spring of spring constant k, then new frequency for this arrangement, is

View SolutionFrequency of oscillation is proportional to
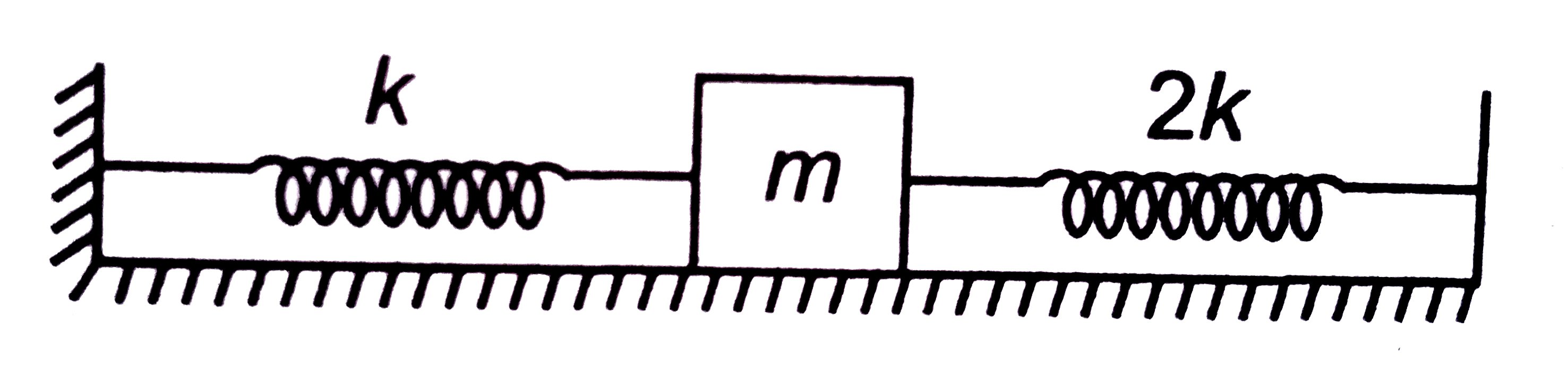
View SolutionIn the figure, `S_(1) and S_(2)` are identical springs. The oscillation frequency of the mass m is f. If one spring is removed, the frequency will become

View SolutionA clock `S` is based on oscillations of a spring and clock `P` is based on pendulum motion, both clocks run at the same rate on Earth. On a planet having the same mass, but twice the radius that of the earth
View SolutionIn case of a forced vibration, the resonance wave becomes very sharp when the
View SolutionThe amplitude of damped oscillator becomes `1/3` in `2s`. Its amplitude after `6s` is `1//n` times the original. The value of `n` is
View SolutionIf the differential equation given by `(d^(2)y)/(dt^(2))+2k(dy)/(dt)+omega^(2)y=F_(0)sin pi t` describes the oscillatory motion of body in a dissipative medium under the influence of a periodic force, then the state of maximum amplitude of the oscillation is a measure of
View Solution
EXERCISE 1 questions and complete solutions for chapter OSCILLATIONS of MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS of Class 12