Complete Solutions to Exercise 1 of chapter KINETIC THEORY OF GASES ANDRADIATION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | KINETIC THEORY OF GASES ANDRADIATION |
| MHTCET PREP GUIDE | Exercise 1 |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
The pressure `p` for a gas is plotted against its absolute temperature `T` for two different volumes `V_(1)` and `V_(2)`. If `p` is plotted on `y-` axis and `T` on `x-`axis, then
View SolutionAir is pumped into an automobile tube upto a pressure of 200 kPa in the morning when the air temperture is `22^(@)C` During the day , temperature ries to `42^(@)C` and the tube expands by 2% a The pressure of the air in the tube at this temperature, will be approximately
View SolutionSimple behaviour under all conditions of real gas is governed by the equation
View SolutionWhen a van der waals ' gas undergoes free expansion , then its temperature
View SolutionAt `10^(@)C`, the value of the density of a fixed mass of an ideal gas divided by its pressure is x. at `110^(@)C`, this ratio is
View SolutionOne litre of an ideal gas st `27^(@)C` is heated at a constant pressure to the `297^(@)C.` Then, the final volume is the approximately
View SolutionTwo ballons are filled, one with pure He gas and other by air, repectively. If the pressure and temperature of these ballons are same then the number of molecules per unit volume is:
View SolutionTwo moles of an ideal gas is contained in a cylinder fitted with a frictionless movalbe piston, exposed to the atmosphere, at an initial temperature `T_(0)`. The gas is slowly heated so that its volume becomes fout times the initial value. The work done by gas is
View SolutionDuring an experiment, an ideal gas is found to obey an additional law `VP^2=constant,` The gas is initially at a temperature T, and volume V. When it expands to a volume `2V,` the temperature becomes…….
View SolutionThe gas in a vessel is subjected to a pressure of `20` atmosphere at a temperature `27^(@)C`. The pressure of the gas in the vessel after one half of the gas is released from the vessel and the temperature of the remainder is raised by `50^(@)C` is
View SolutionA real gas behaves like an ideal gas if its
View SolutionHow much heat energy in joules must be supplied to 14gms of nitrogen at room temperature to rise its temperature by `40^(@)C` at constant pressure? (Mol. Wt. of `N_(2)=28gm`, R=constant)
View SolutionA balloon contains `500m^(3)` of He at `27^(@)C` and 1 atm pressure. Then , the volume of He at `-3^(@)C` and 0.5 atm pressure will be
View SolutionThe figure below shows the plot of `(PV)/(nT)` versus P for oxygen gas at two different temperatures
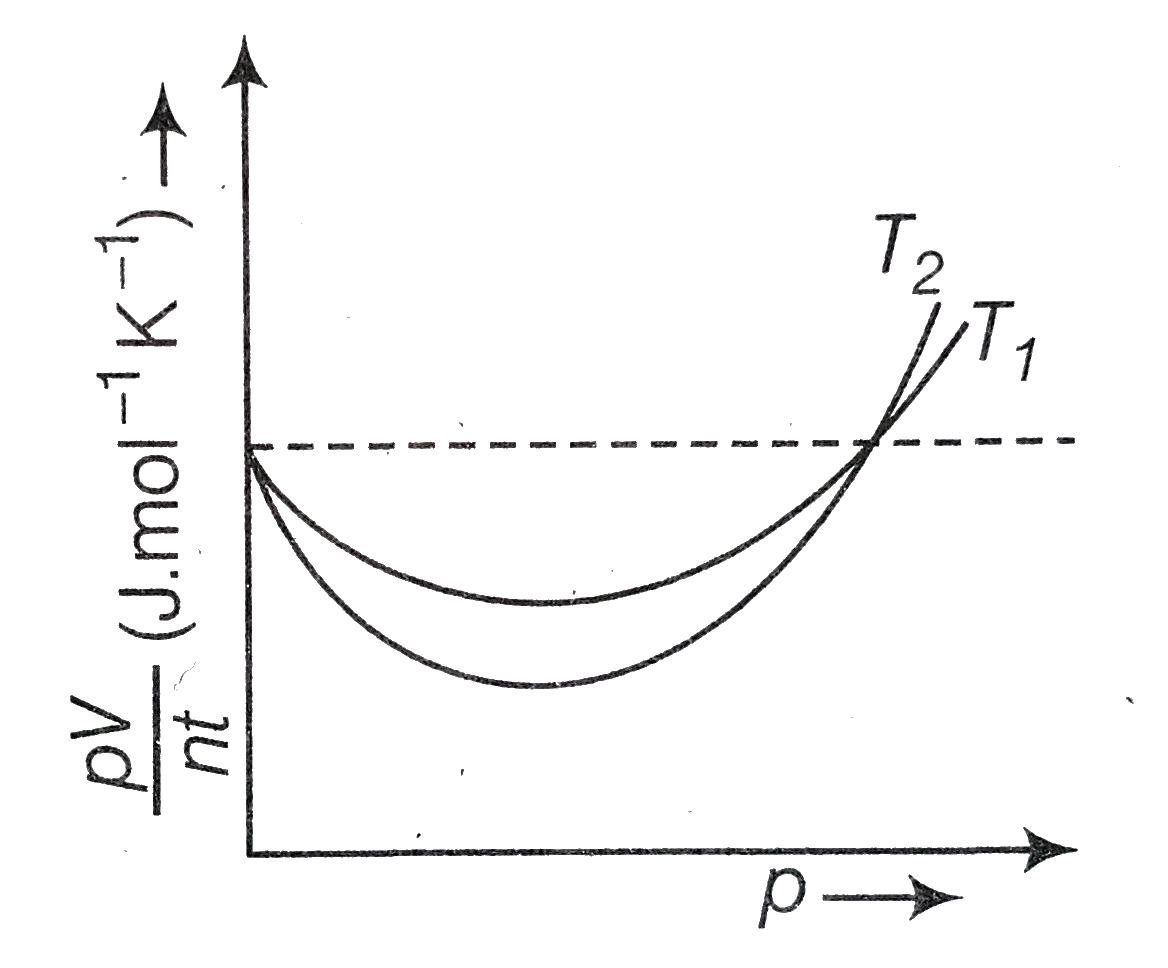
Read the following statements concerning the above curves.
(i) The dotted line corresponds to the ideal gas behaviour
(ii) `T_(1)gtT_(2)`
The value of `(pV)/(nT)` at the point where the curves meet on the y-axis is the same for all gases Which of the above statements is true ?
View SolutionTemperature remaining constant, the pressure of gas is decreased by 20%. The percentage change in volume
View SolutionA closed container of volume `0.02m^(3)` contains a mixture of neon and argon gases at a temperature `27^(@)C` and pressure `1 xx 10^(5) Nm ^(-1)` The total mass is 28 and the molar mass of and argon are `20` and `40` respectively find the masses of individual gases in the container assuming then to be ideal .
View SolutionThe mean free path of collision of gas melecules varies with its diameter (d) of the molecules as
View SolutionAt what temperature will be the oxygen molecules have the same root mean square root mean square speed as hydrogen molecules at 300 K ?
View SolutionThe temperature of an ideal gas is increased from 120 K to 480 K. If at 120 K the root mean square velocity of the gas molecules is v, at 480 K it becomes
View SolutionThe temperature at which the mean KE of the molecules of gas is one - third of the mean KE of its molecules at `180^(@)C` is
View Solutionif average velocity becomes 4 times, then what will be the effect on rms velocity at the temperature?
View SolutionFor real gases (van der waals ' gas )
View SolutionThe root mean square velocity of a gas molecule of mass m at a given temperature is proportional to
View SolutionWhen temperature of an ideal gas is increased from `27^(@)C" to "227^(@)C` , its rms speed is changed from `400ms^(-1) " to "V_(s)` . Then , the `V_(s)` is
View SolutionRoot mean square velocity of gas molecules is `300 m//sec`. The `r.m.s` velocity of molecules of gas with twice the molecular weight and half the absolute temperature is :
View SolutionN molecules , each of mass m, of gas A and 2 N molecules , each of mass 2m, of gas B are contained in the same vessel which is maintained at a temperature T. The mean square velocity of molecules of B type is denoted by ` V_(2)` and the mean square velocity of A type is denoted by `V_(1)` then `(V_(1))/(V_(2))` is
View SolutionAt a certain temperature , the ratio of the rms velocity of `H_(2)` molecules to `O_(2)` molecule is
View SolutionIf the molecular weight of two gases are `M_(1)` and `M_(2)` then at a temperature the ratio of rms velocity `C_(1) and C_(2)` will be
View SolutionThe temperature at which the velocity of oxygen will be half of hydrogen at NTP is
View Solution10 moles of an ideal monoatomic gas at `10^(@)C` are mixed with 20 moles of another monoatomic gas at `20^(@)C`. Then the temp. of the mixture is
View SolutionThe speed of sound in hydrogen is `1270 ms^(-1)` at temperature T. the speed at the same T in a mixture of oxygen and hydrogen mixed in a volume ratio 1:4 will be ?
View SolutionThe ratio of the velocity of sound in Hydrogen gas `(gamma=7/5)` to that in Helium gas `(gamma=5/3)` at the same temperature is `sqrt(21/3)`.
View SolutionIf at NTP, velocity of sound in a gas is 1150 m/s, then find out the rms velocity of gas molecules at NTP. (Given R=8.3J/mol/K, `C_(P)=4.8` cal/mol/k).
View SolutionIf `c_(s)` is the velocity of sound in air and c is rms velocity , then
View SolutionThe root mean square velocity of the molecules in a sample of helium is `5//7th` that of the molecules in a sample of hydrogen. If the temperature of hydrogen sample is `0^(@)C`, then the temperature of the helium sample is about
View SolutionWhich one of the following is not an assumption in the kinetic theory of gases?
View SolutionTwo vessels A and B having equal volume contain equal masses of hydrogen in A and helium in B at 300 K. Then, mark the correct statement?
View SolutionOne mole of diatomic ideal gas undergoes a cyclic process ABC as show in figure . The process BC is adiabatic. The temperature at A,B and C are 400K, 800Kand 600 K, respectively . Choose the correct statement.
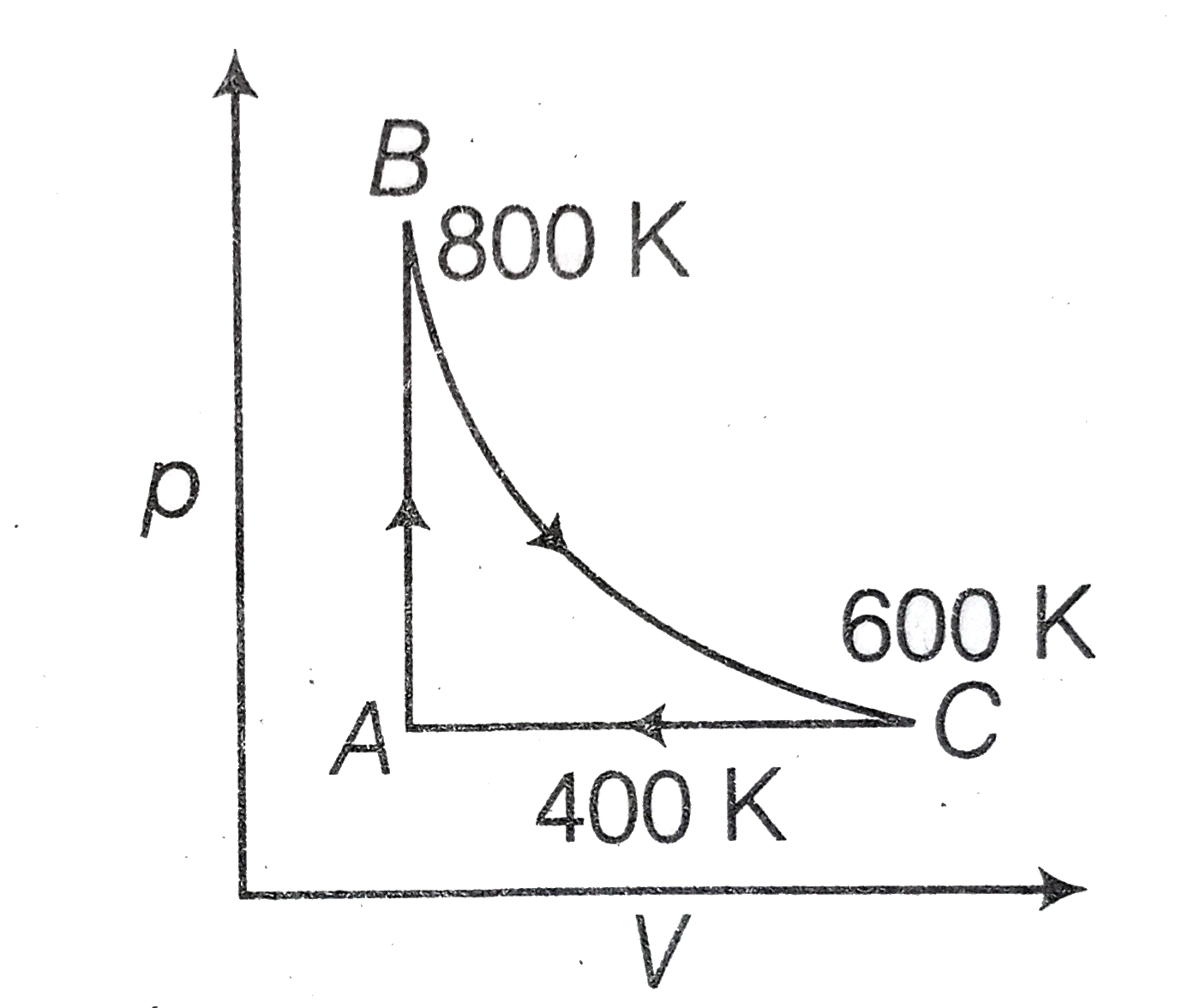
View SolutionOne kg of a diatomic gas is at pressure of `8xx10^4N//m^2`. The density of the gas is `4kg//m^3`. What is the energy of the gas due to its thermal motion?
View SolutionA sealed container with negiligible coefficient of volumetric expansion contains helium (a monatomic gas). When it is heated from 300 K to 600 K, the average KE of helium atoms is
View SolutionAt what temperarture, the kinetic energy of a gas molecule is half of the value at `27^(@)C.` ?
View SolutionTwo perfect monoatomic gases at absolute temperature `T_(1)` and `T_(2)` are mixed. There is no loss of energy. Find the temperature of the mixture if the number of moles in the gases are` n_(1)` and `n_(2)`.
View SolutionThe kinetic energy of one mole gas at 300 K temperature , is E. at 400 K temperature kinetic energy is E' . The value of `E'//E` is
View SolutionHow much should the pressure be increased in order to decrease the volume of a gas 5% at a constant temprature ?
View SolutionFor a gas the differce between the two specific heat is `4150 J//kg K`. What is the specific heat at constant volume of gas if the ratio of sepcific heat is 1.4
View SolutionA molecule of a gas has six degrees of freedom Then , the molar specific heat of the gas at constant volume is
View SolutionWhich one of the following gases possesses the largest internal energy
View SolutionValue of two principal specific heats of a gas `("in cal mol" K)^(-1)` determined by different students are given . Which is most relible ?
View SolutionCaluculate Change in internal energy when 5 moles of hydrogen is heated to `20^(@)C` from , Specific heat of hydrogen at constant pressure is 8 cal `("mol"^(@)C)^(-1)`
View SolutionEach molecule of a gas has F degrees of freedom . The ratio `(C_(p))/(C_(V))=gamma` for the gas is
View SolutionThe adiabatic elasticity of hydrogen gas `(gamma=1.4)` at `NTP`
View Solutionif quantity of heat 1163.4 J supplied to one mole of nitrogen gas , at room temperture at constant pressure , then the rise in temperature is
View Solutionusing euipartion of energy, the specific heat (in `Jkg^(-1)K^(-1)`)of aluminium at room temperature can be estimated to be (atomic weigh of aluminium=27)
View SolutionFor a gas if ratio of specific heats at constant pressure and volume is g then value of degrees of freedom is
View SolutionOne mole of an ideal monoatomic gas requires 207 J heat to raise the temperature by 10 K when heated at constant pressure. If the same gas is heated at constant volume to raise the temperature by the same 10 K, the heat required is [Given the gas constant R = 8.3 J/ mol. K]
View SolutionWhich of the given substances A B and C have more specific heat ?
View SolutionFor the same rise in temperature of one mole of gas at constant volume , heat required for a non - linear tratomic gas is K times that required for monoatomic gas . The value of K is
View SolutionA gas expands with temperature according to the relation `V=KT^(2/3)`.Work done when the temperature changes by 60K is.
View SolutionA system is taken through a cyclic proceses represented by a circle as shown in the figure. The heat absorbed by the system is

View Solution`C_(v)" for "O_(2)" is " (5)/(2)R` with increase in tempeature it becomes `(7)/(2)R` due to a
View SolutionA given mass of a gas is compressed isothermally until its pressure is doubled. It is then allowed to expand adiabatically until its original voume is restored and its pressure is then found to be 0.75 of its initial pressure. The ratio of the specific heats of the gas is approximately.
View Solution310 J of heat is required to rise the temperature of 2 moles of an ideal gas at constant pressure from `25^(@)C` to `35^(@)C`. The amount of heat required to raise the temperature of the gas through the same range at constant volume, is
View SolutionTwo cylinders A and B fitted with pistons contain equal amounts of an ideal diatomic gas at 300K. The piston of A is free to move, while that B is held fixed. The same amount of heat is given to the gas in each cylinder. If the rise in temperature of the gas in A is 30K, then the rise in temperature of the gas in B is
View SolutionThe ratio of the specific heats `C_(p)/C_(v)=gamma` in terms of degrees of freedom (n) is given by
View SolutionDuring an adiabatic process , the pressure p of a fixed mass of an ideal gas change by `Deltap`and its volume V change by `DeltaV` . If `gamma=C_(p)//C_(v)` then `DeltaV//V` is given by
View SolutionA thermodynamic system is taken from state A to state B along ABC and is brought back to A along BDA as shown in figure . Net work done during one complete cycle is given by area

View SolutionIn a p-V diagram for an ideal gas (Where , p is along y-axis and V is along X- axis) , the value of the ratio "slope pof adiabatic curve/ Slope of the isothermal curve"at any point will be (Where symbols have their usual meanings ).
View SolutionIn the following p-v diagram figure two adiabates cut two isothermals at `T_(1)andT_(2)`. The value `V_(b)//V_(c)` is

View SolutionIn the indicator diagram , `T_(a),T_(b),T_(c),T_(d)` represents temperatures of gas at A,B,C,D respectively Which of the following is correct relation?

View SolutionDuring adiabatic expansion the increase in volume is associated with
View SolutionThe change in the entropy of a 1 mole of an ideal gas which went through an isothermal process form an initial state `(P_1,V_1,T)` to the final state `(P_2,V_2 , T)` is equal to
View SolutionAt `27^(@)C` a motor car tyre has pressure of 2 atmosphere. Find the temperautre. If the tyre suddenly bursts. (Given, `gamma_("air")=1.4`)
View SolutionA gas is compressed at a constant pressure of `50N//m^(2)` from a volume `10m^(3)` to a volume of `4m^(3)`. 100J of heat is added to the gas then its internal energy is
View SolutionFigure shows four p-V diagrams . Which of these curves represent isothermal and adiabatic process?

View SolutionA gas at pressure P is abiabatically compressed so that its density becomes twice that of initial value. Given that `gamma=C_(p)//C_(v)=(7//5)` , What will be the final pressure of the gas ?
View SolutionIf an average jogs, he produces `14.5xx10^(3)` cal/min. This is removed by the evaporation of sweat. The amount of sweat evaporated per minute (assuming 1 kg requires `580xx10^(3)` cal for evaporation) is
View SolutionFigure shows a thermodynamic process on one mole of a gas . How does the work done in the process changes with time ?

View SolutionA cyclic process is shown is shown in figure . Work done during isobaric expansion is

View SolutionWhen `1 kg` of ice at `0^(@)C` melts to water at `0^(@)C`, the resulting change in its entropy, taking latent heat of ice to be `80 cal//g` is
View SolutionTwo temperature scales A and B are related by :
`(A-42)/(110)=(B-72)/(220)`
At which temperature two scales have the same reading ?
View SolutionAt ordinary temperatures, the molecules of an ideal gas have only translational and rotational kinetic energies. At high temperatures they may also have vibrational energy.
As a result of this, at higher temperature
View SolutionIn a certain process, 400 cal of heat are supplied to a system and the same time 105 J of mechanical work done on the system . The increase in its internal energy is
View SolutionA gas is expanded from volume `V_(0)" to "2V_(0)` three different processes shown in figure.
Process 1 is isobaric process, 2 is isothermal and process 3 is adiabatic . Let `DeltaU_(1),DeltaU_(2)andDeltaU_(3)` be the change in internal energy of the gas in these three processes . Then ,

View SolutionWhat is the nature of change in internal energy in the following three thermodynamic processes shown in figure ?

View Solution`1 cm^(3)` of water at its boiling point absorbs `540 cal` of heat to become steam with a volume of `1671 cm^(3)`. If the atmospheic pressure is `1.013 xx 10^(5) N//m^(2)` and the mechanical equivalent of heat `= 4.19 J//cal`, the energy spent in this process in overcoming intermolecular forces is
View SolutionFive moles of hydrogen `(gamma = 7//5)`, initially at `STP`, is compressed adiabatically so that its temperature becomes `400^(@)C`. The increase in the internal energy of the gas in kilojules is `(R = 8.30 J//mol-K)`
View SolutionThree copper blocks of masses `M_(1), M_(2) and M_(3) kg` respectively are brought into thermal contact till they reach equlibrium. Before contact, they were at `T_(1), T_(2), T)(3),(T_(1)gtT_(2)gtT_(3))`. Assuming there is no heat loss to the surroundings, the equilibrium temperature `T` is `(s is specific heat of copper)`
View SolutionA gas is suddenly compressed to `1/4th` of its original volume. Caculate the rise in temperature when original temperature is `27^(@)C. gamma= 1.5`.
View SolutionA cylinder of fixed capacity (of 44.8 L) contains 2 moles of helium gas at STP .What is the amount of heat needed to raise the temperature of the gas in the cylinder by `20^(@)C` ? `("Use"R=8.31J"mol"^(-1)K^(-1))`
View SolutionThe temperature of sink of Carnot engine is `27^(@)C`. Efficiency of engine is `25%`. Then temeperature of source is
View SolutionChoose the incorrect statement from the following:
S1: The efficiency of a heat engine can be 1, but the coefficient of performance of a refrigerator can never be infinity
S2: The first law of thermodynamics is basically the principle of conservation of energy
S3: The second law of thermodynamics does not allow several phenomena consistent with the first law
S4: A process, whose sole result is the transfer of heat from a colder object to hotter object is impossible
View SolutionThe temperature -entropy diagram of a reversible engine cycle is given in the figure.Its efficiency is
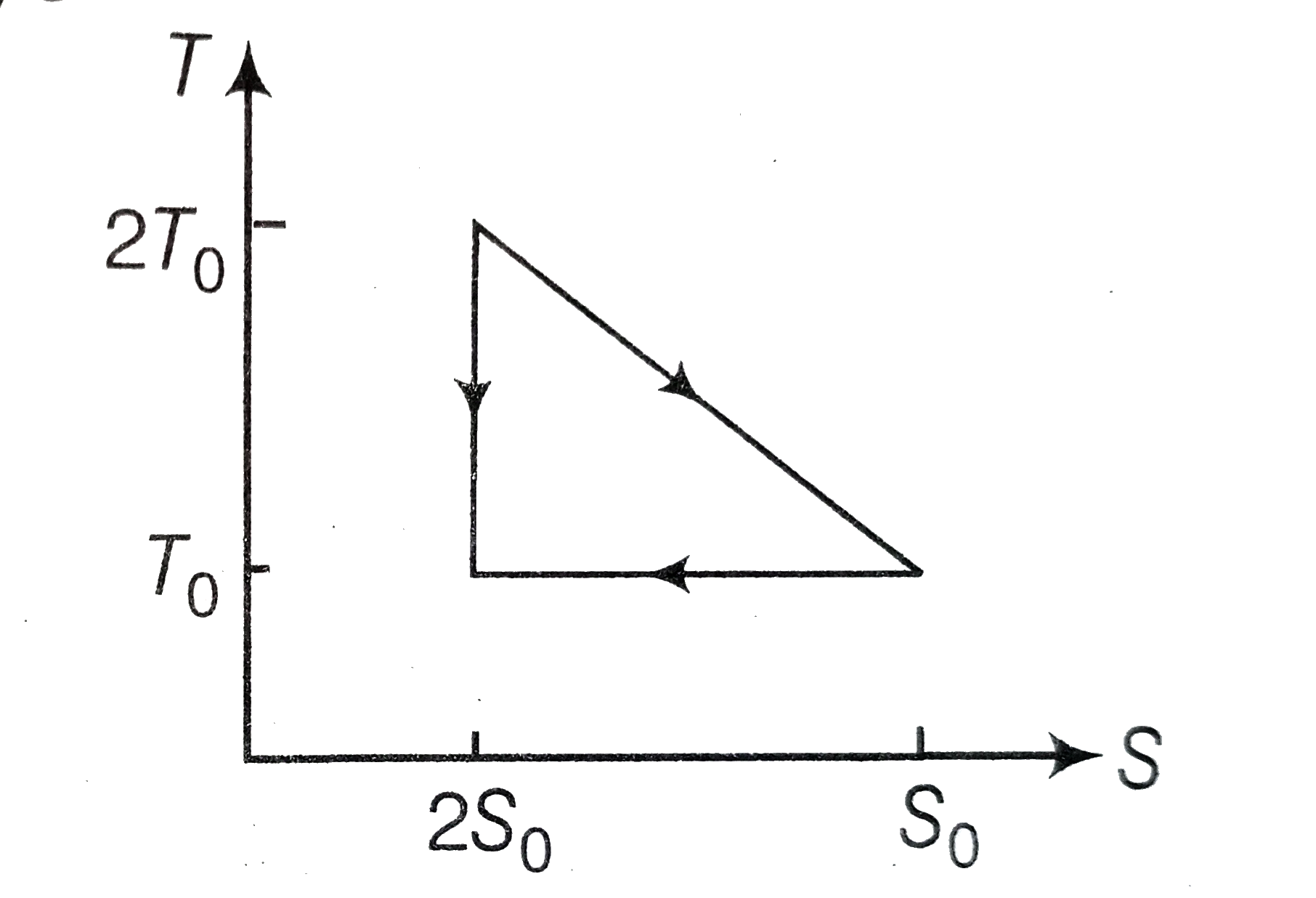
View SolutionA carnot's engine works between a source at a temperature of `27^(@)C` and a sink at `-123 ^(@)C`. Its efficiency is
View SolutionA engine has an efficiency of `1//3`. The amount of work this engine can perform per kilocalorie of heat input is
View SolutionThe coeffcient of performance of a refrigerator working between `10^(@)C` and `20^(@)C` is
View SolutionA Carnot engine used first ideal monoatomic gas and then an ideal diatomic gas , if the source and sink temperatures are `411^(@)C` and `69^(@)C` ,respectively and the engine extracts 1000 J of heat from the source in each cycle , then
View SolutionA body having `110 and70^(@)C` temperatures of surrounding and of itself repectively . What would be the value of coefficient of performance ?
View SolutionWhat is the source temperature of the carnot engine reuired to get 70 % efficiency ?
View SolutionA carnot engine operates with source at `127^(@)C` and sink at `27^(@)C`. If the source supplies `40kJ` of heat energy. The work done by the engine is
View SolutionA carnot engine has efficiency `1//5` . Efficiency becomes `1//3` when temperature of sink is decreased by 50 K What is the temperature of sink ?
View Solution
Exercise 1 questions and complete solutions for chapter KINETIC THEORY OF GASES ANDRADIATION of MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS of Class 12