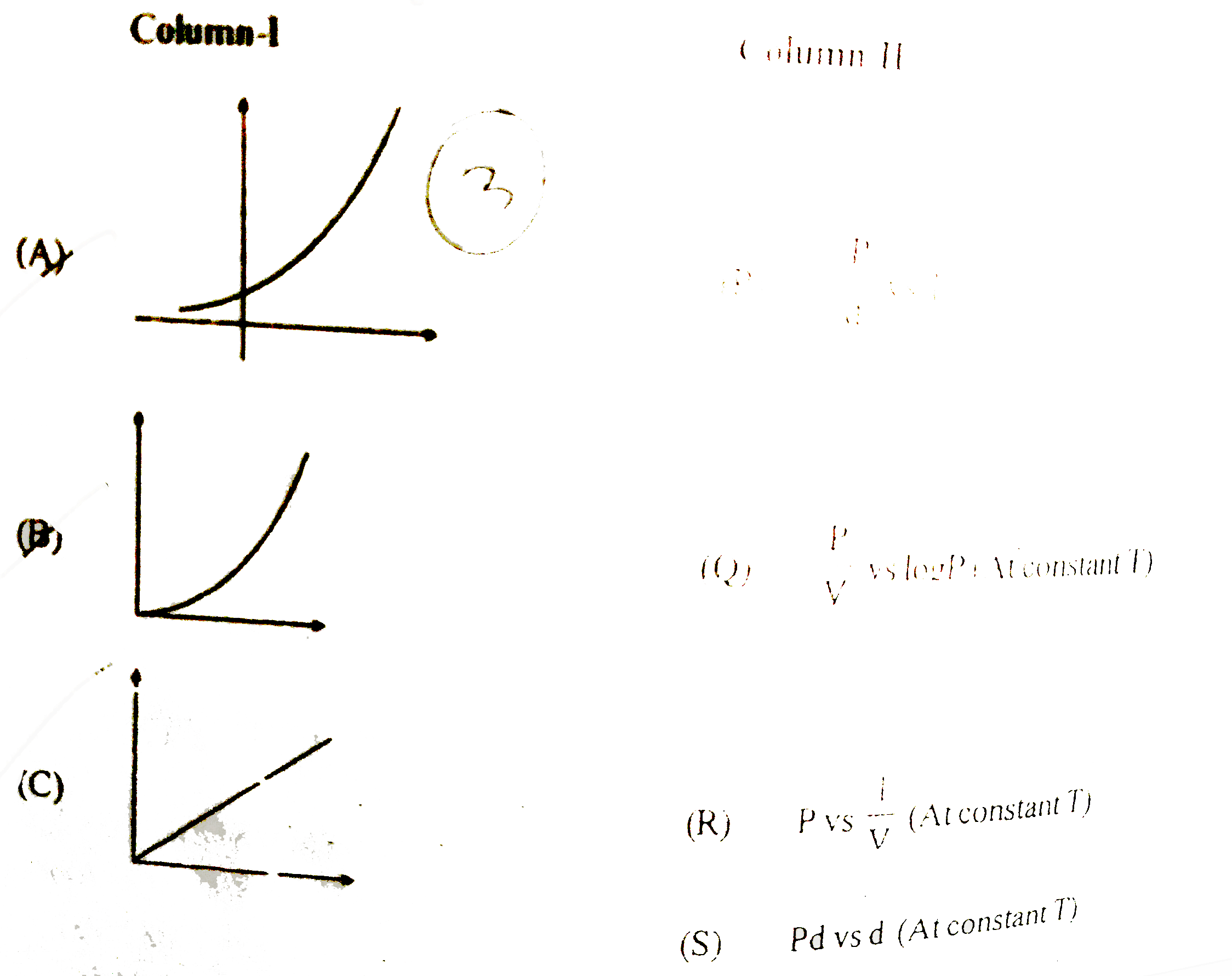At 10∘C, the value of the density of a fixed mass of an ideal gas divided by its pressure is x. at 110∘C, this ratio is
A
x
B
383283x
C
10110x
D
283383x
Video Solution
Text Solution
The correct Answer is:D
From ideal gas law, pV=nRTorpV=mMRT
pVm=1MRTorPp=RTM⇒pP=1T
∴ ρ1/p1ρ2/p2=T2T1⇒x(ρ2/P2)=383283
or ρ2P2=283383
|
Topper's Solved these Questions
- KINETIC THEORY OF GASES ANDRADIATIONBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - KINETIC THEORY OF GASES ANDRADIATIONEXERCISE - Exercise 2
50 Videos
- KINETIC THEORY OF GASES ANDRADIATIONBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - KINETIC THEORY OF GASES ANDRADIATIONEXERCISE - MHT CET Corner
40 Videos
- KINETIC THEORY OF GASES ANDRADIATIONBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - KINETIC THEORY OF GASES ANDRADIATIONEXERCISE - MHT CET Corner
40 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHT BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHT EXERCISE - MHT CET Corner
24 Videos
- MAGNETIC EFFECT OF ELECTRIC CURRENTBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - MAGNETIC EFFECT OF ELECTRIC CURRENTEXERCISE - MHT CET CORNER
20 Videos
Similar Questions
Knowledge Check
At 10∘C, the density of a fixed mass of an ideal gas divided by its pressure is X. At 110∘C, this ratio would be
A10x110B283x383CxD383283 XA 0∘C the density of a fixed mass of a gas divided by pressure is x. At 100∘C, the ratio will be
AxB273373xC373273xD100273xFor a fixed mass of an ideal gas the correct representation is:
A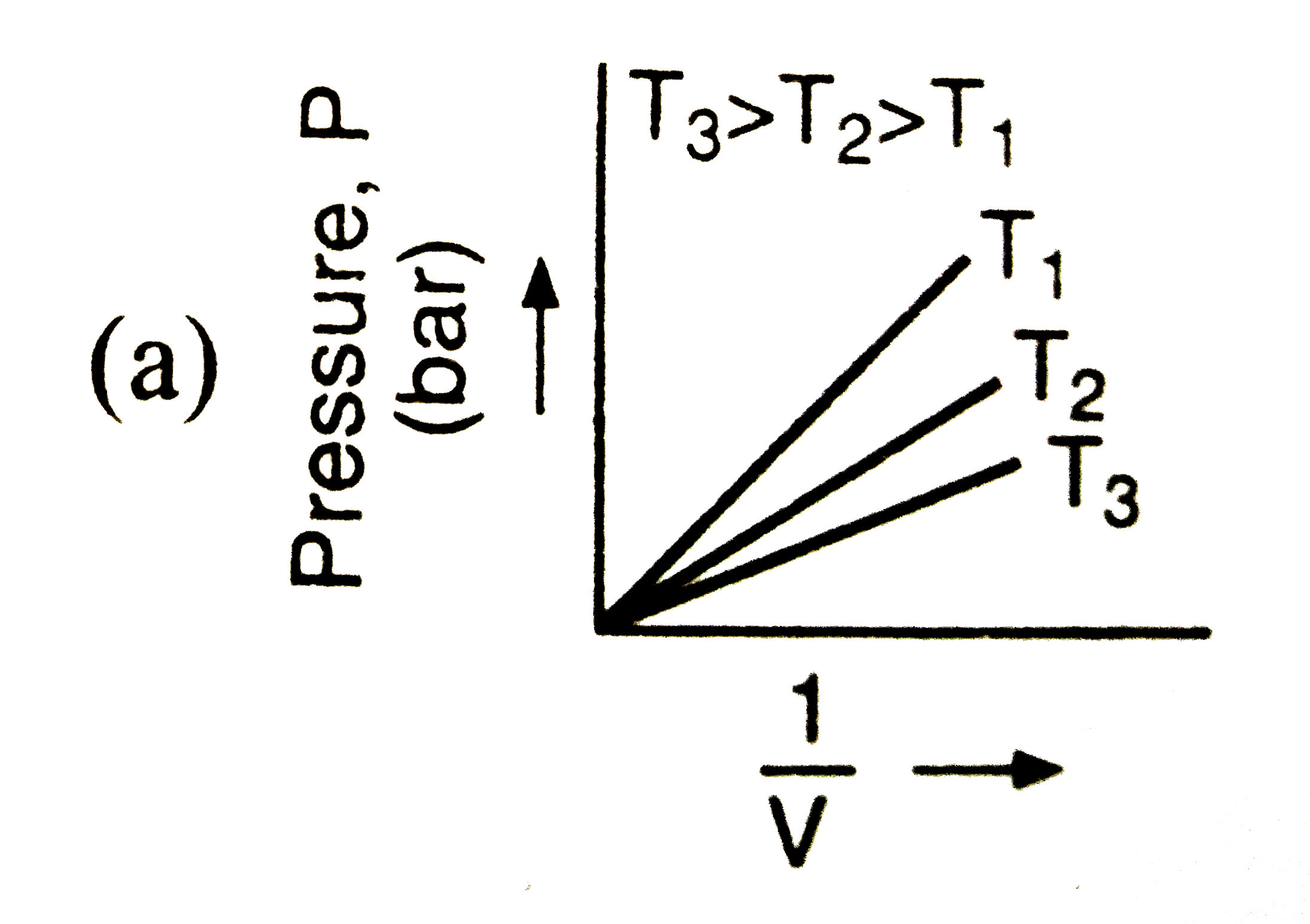 B
B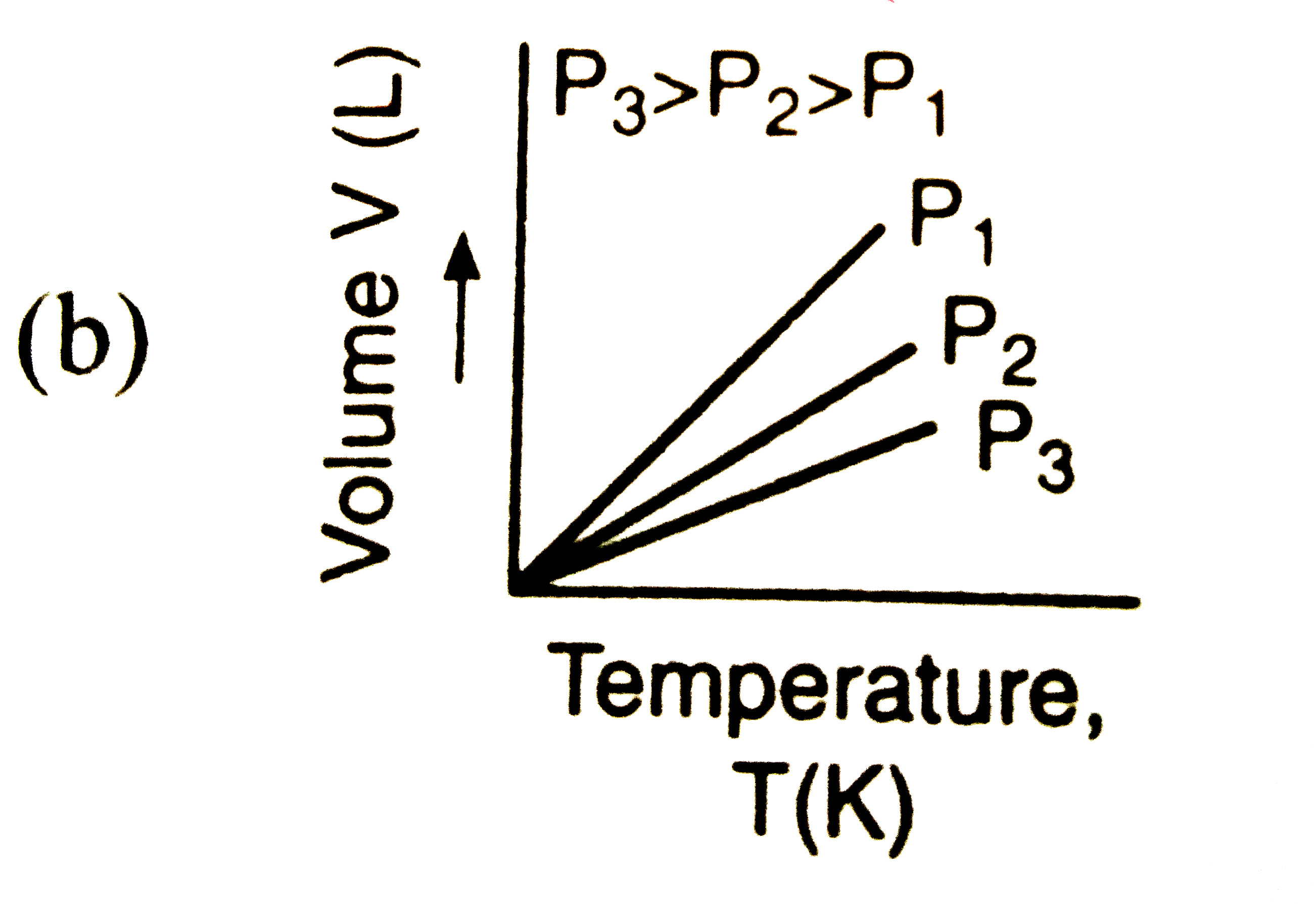 C
C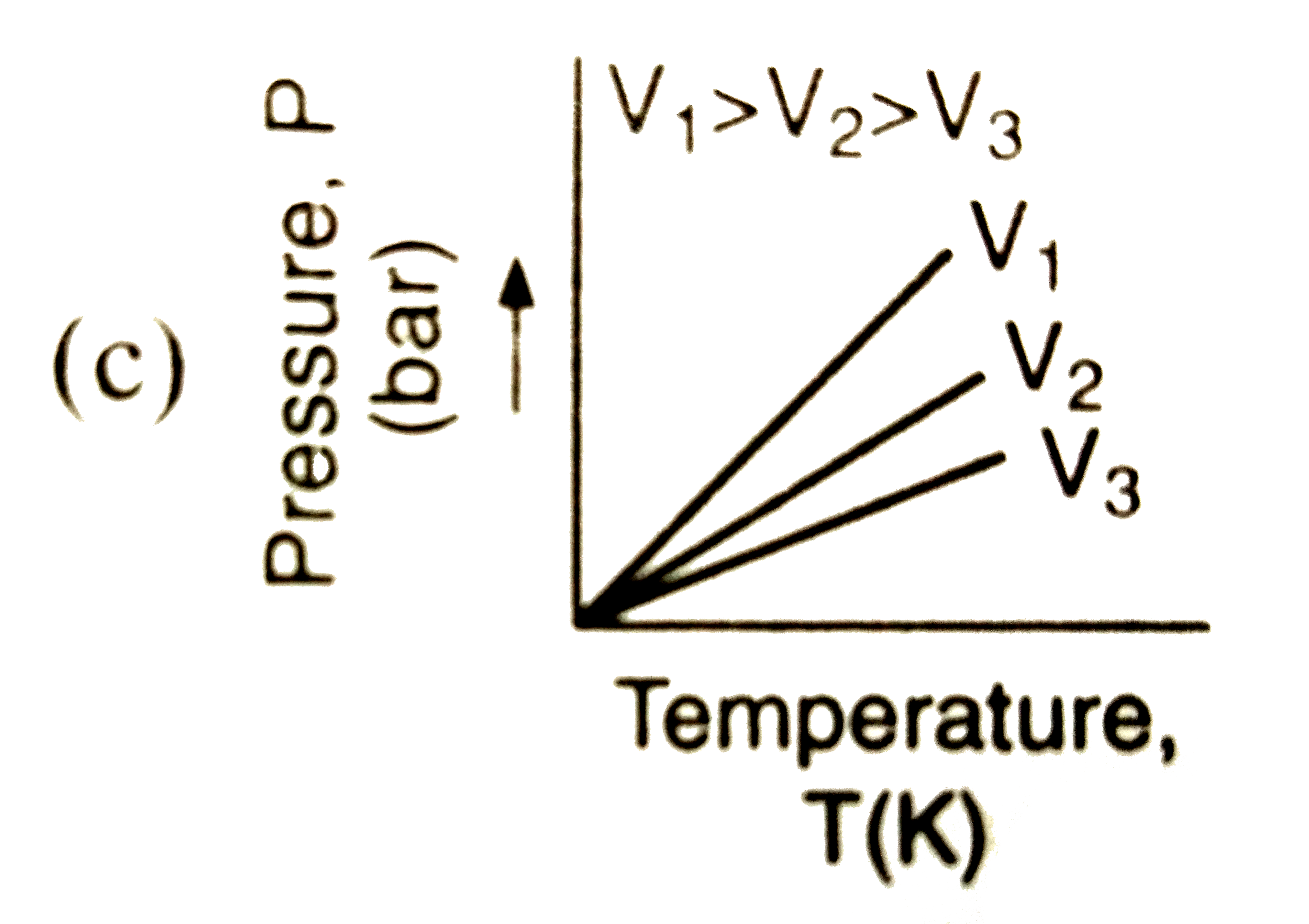 D
D
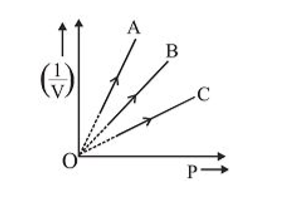
Figure shows the isotherms of fixed mass of an ideal gas at three temperatures TA.TB and TC then:-
View SolutionThe energy density uV of an ideal gas is related to its pressure P as
View SolutionThe ratio of the density and pressure of a fixed mass of an ideal gas is "5" at 10°C. Then this ratio at 110°C is
View SolutionAt constant pressure , the volume of fixed mass of an ideal gas is directly proportional to
View SolutionIf E is the energy density in an ideal gas, then the pressure of the ideal gas is
View Solution