Complete Solutions to Objective Type Question (A. Multiple Choice Questions) of chapter PROBABILITY of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | PROBABILITY |
| MODERN PUBLICATION | Objective Type Question (A. Multiple Choice Questions) |
| Number Of Questions | 50 |
| Academic Year | 2023-24 |
If `P(A) =1/2`, `P (B) = 0`, then `P (A|B)` is
View SolutionIf `A` and `B` are two events such that `A nn B > phi, P(A/B) = P(B/A)`. Then,
View SolutionThe probability of obtaining an even prime number on each die, when a pair of dice is rolled is
View SolutionTwo events A and B are said to be independent if :
View SolutionProbability that A speaks truth is `4/5` . A coin is tossed. A reports that a appears. The probability that actually there was head is
View SolutionIf A and B are two events such that `AsubB` and `P(B)!=0,` them which of the following is correct?
View SolutionIf A and B are two events such that
`P(A) ne0` and `P(B//A)=1,` then :
View SolutionIf P(A]B) > P(A), then which of the following is correct:
View SolutionIf A and B are any two events such that `P(A)+P(B)-P( A "and" B)=P(A)`, then:
View SolutionThe mean of the numbers obtained on throwing a die having written 1 on three faces, 2 on two faces and 5 on one face is
View SolutionSuppose that two cards are drawn at random from a deck of cards. Let X be the number of aces obtained. Then the value of E(X) is
View SolutionIn a box containing 100 bulbs, 10 are defective. The probability that out of a sample of 5 bulbs, none is defective is
View SolutionThe probability that a student is not a swimmer is `1/5`. Then the probability that out of five students, four are swimmers is
View SolutionA die is thrown once, then the probability of getting a number greater than 3 is :
View SolutionLet A and B be two events. If P(A) = 0.2, P(B)=0.4, `P(A uu B)=0.6`, then `P(A//B)` is equal to :
View SolutionLet A and B be two events such that `P(A)=0.6, P(B)=0.2` and `P(A//B)=0.5`. Then `P(A'//B')` equals :
View SolutionIf E and F are independent events such that `0ltP(E)lt1 and 0ltP(F)lt1,` then
View SolutionLet 'X' be a discrete random variable. The probability distribution of X is given below :
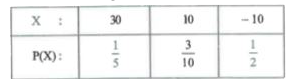
Then E(X) is equal to :
View SolutionIf X be a random variable taking values `x_(1),x_(2),x_(3),….,x_(n)` with probabilities `P_(1),P_(2),P_(3)`,…..`P_(n)`, respectively. Then, Var (x) is equal to …….. .
View SolutionIf A and B two events such that P(A)=0.2, P(B)=0.4 and `P(A cup B)=0.5`, then value of `P(A//B)` is ?
View SolutionAn urn contains 6 balls of which two are red and four are black. Two balls are drawn at random. Probability that they are of the different colours is
View SolutionIf E and F are independent events, `P(E)=(1)/(2)` and `P(F)=(1)/(3)`, then `P(E nn F)` is :
View SolutionThe probability of obtaining an even prime number on each die, when a pair of dice is rolled is
View SolutionIf `P(A)=0.8, P(B)=0.5` and `P(B/A)=0.4,` then find P(A/B)
View SolutionIf `P(A)7/(13),P(B)=9/(13)` and `P(AnnB)=4/(13),` find `P(A/B)dot`
View Solutionif `A` and `B` be two events such that `P(A)=1/4, P(B)=1/3` and `P(AuuB)=1/2,` show that `A` and `B` are independent events.
View SolutionIf `P(A)=(1)/(2),P(B)=0`, then P(A/B) is :
View SolutionThe probability of obtaining an even prime number on each die, when a pair of dice is rolled is
View SolutionIf P (E) denotes probability of occurrence of event E, then :
View SolutionIf A and B are independent events, then :
View SolutionThe probability of obtaining an even prime number on each die, when a pair of dice is rolled is(A) 0 (B) `1/3`(C) `1/(12)` (D) `1/(36)`
View SolutionIf `Aa n dB` are two events such that `P(A)=0. 5 ,P(B)=0. 6a n dP(AuuB)=0. 8` , find `P(A//B)a n dP(B//A)dot`
View SolutionIf A and B are two independent events such that `P(AuuB)=0. 60\ a n d\ P(A)=0. 2` , find `P(B)dot`
View SolutionTwo cards are drawn from a well shuffled deck of $2 cards with replacement The probability that both cards are queens, is
View SolutionEvents A and B are independent if
View SolutionA pair of dice is thrown once, the probability of doublet is :
View SolutionIf `P(A)=(1)/(2)` and `P(B)=0`, then `P(A//B)` is equal to :
View SolutionIf A and B are events such that `P(A//B)=P(B//A)`, then :
View SolutionA die is rolled. If the outcome is an odd number, what is the probability that it is prime?
View SolutionIf `P(A)=(3)/(5)` and `P(B)=(1)/(5)`, then the value of `P(A nn B)` when A and B are independent events is :
View SolutionIf A and B are two independent events and `P(A)=(1)/(4),P(B)=(1)/(3)`, then :
View SolutionIf `P(A)=(1)/(2),P(B)=(3)/(8)` and `P(A nn B)=(1)/(5)`, then `P(A//B)` is equal to :
View SolutionIf P(A]B) > P(A), then which of the following is correct: (A) `P(B" "|" "A)" "<" "P(B)` (B) `P(AnnB)" "P(B)` (D) `P(B" "|" "A)" "=" "P(B)`
View SolutionIf A and B are any two events such that `P(A)+P(B)-P( A "and" B)=P(A)`, then:
View SolutionThe probability of obtaining an even prime number on each die, when a pair of dice is rolled is(A) 0 (B) `1/3`(C) `1/(12)` (D) `1/(36)`
View SolutionLet E and F be two events associated with the same random experiment. Then E and F are said to be independent if `P(E nn F)` is equal to :
View SolutionThe probability that a student is not a swimmer is `1/5`. Then the probability that out of five students, four are swimmers is (A) `^5C_4(4/5)^41/5` (B) `(4/5)^41/5`(C) `^5C_1 1/5(4/5)^4` (D) None of these
View SolutionA card is drawn from a well shuffled deck of 52 cards. The probability of red queen is :
View SolutionIf A and B are events such that `P(A//B)=P(B//A)`, then :
View SolutionThe probability of obtaining an even prime number on each die, when a pair of dice is rolled is(A) 0 (B) `1/3`(C) `1/(12)` (D) `1/(36)`
View Solution
Objective Type Question (A. Multiple Choice Questions) questions and complete solutions for chapter PROBABILITY of ARIHANT MATHS (HINGLISH) of Class 12
All Exercises from MODERN PUBLICATION Class 12 MATHS PROBABILITY
- CHAPTER TEST
- CHECK YOUR UNDERSTANDING
- COMPETITION FILE
- EXAMPLES
- Exercise
- EXERCISE 13 (a) (LATQ)
- EXERCISE 13 (a) (SATQ)
- EXERCISE 13 (b) (LATQ)
- EXERCISE 13 (b) (SATQ)
- EXERCISE 13 (c) (SATQ)
- EXERCISE 13 (d) (LATQ)
- EXERCISE 13 (e) (LATQ)
- EXERCISE 13 (e) (SATQ)
- EXERCISE 13 (f) (LATQ I)
- EXERCISE 13 (f) (LATQ II)
- EXERCISE 13 (f) (SATQ)
- EXERCISE 13 (g) (LATQ)
- EXERCISE 13 (g) (SATQ)
- EXERCISE 13 (h) (LATQ)
- Miscellaneous Exercise on Chapter 13
- MOCK TEST (Answer the following questions)
- MOCK TEST (Fill in the blanks)
- MOCK TEST (Select the correct option)
- MOCK TEST SECTION D
- NCERT-FILE (Exercise 13.1)
- NCERT-FILE (Exercise 13.2)
- NCERT-FILE (Exercise 13.3)
- NCERT-FILE (Exercise 13.4)
- NCERT-FILE (Exercise 13.5)
- Objective Type Question (A. Multiple Choice Questions)
- Objective Type Question (B. Fill in the Blanks)
- Objective Type Question (C. True/False Questions)
- Objective Type Question (D. Very Short Answer Tyep Questions)
- Revision Exercise