Complete Solutions to Objective Type Question (D. Very Short Answer Tyep Questions) of chapter PROBABILITY of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | PROBABILITY |
| MODERN PUBLICATION | Objective Type Question (D. Very Short Answer Tyep Questions) |
| Number Of Questions | 25 |
| Academic Year | 2023-24 |
If `P(E)=0.6,P(F)=0.3` and `P(E nn F)=0.2`, then find `P(E//F)`.
View SolutionIf `P(A)=0.3,P(B)=0.6` and A and B are independent events, then find the value of P(A and B).
View SolutionThere are 4 white and 6 black balls in a bag. Two balls are drawn at random. Find the probability that both balls drawn are black.
View SolutionFind the probability of drawing a king from a well shuffled pack of 52 cards.
View SolutionIf `P(A)=0.6,P(B)=0.5` and `P(A//B)=0.3`, then find `P(A uu B)`.
View SolutionIf A and B are two events such that `P(A)=0.4, P(B)=0.8` and `P(B//a)=0.6`, then find:
(i) `P(AnnB)` (ii) `P(AuuB)` (iii) `P(A//B)`
View SolutionIf A and B are two events such that `P(A)=0.3,P(B)=0.6` and `P(B//A)=0.5`, find `P(A//B)`.
View SolutionIf two events A and B are such that P(A) =0.3, P(B)=0.4 and `P(A'nnB') =0.5.` then find the value of `P(B//(AuuB')).`
View SolutionIf `P(A)=0.3,P(B)=0.6,P(B//A)=0.5`, find `P(A uu B)`.
View SolutionIf A, B, C are mutually exclusive and exhaustive events associated to a random experiment, then write the value of `P(A)+P(B)=P(C)dot`
View SolutionIf A and B are two independent events such that `P(A)=0.3` and `P(A uu bar(B))=0.8`, find P(B).
View SolutionIf `P(A)=0.35,P(A uu B)=0.60`, find P(B), where A and B are independent events.
View SolutionLet A and B be two independent events such that `P(A)=(1)/(4)` and `P(B)=(1)/(2)`, find P(not A and not B).
View SolutionA die is thrown. If E is the event 'the number appearing is a multiple of 3' and F be the event 'the number appearing is even', then find whether E and F are independent.
View SolutionOne card is drawn at random from a pack of well-shuffled deck of 52 cards. Check whether the following events are independent :
E: 'the card drawn is black'
F: 'the card drawn is a king'.
View SolutionIf A and B are independent events such that `P(A)=p ,\ P(B)=2p\ a n d\ P` (Exactly one of A and B occurs )`=5/9` , find the value of `pdot`
View SolutionWrite the probability that a number selected at random from the set of first 100 natural numbers is a cube.
View SolutionThree numbers are chosen from 1 to 20. Find the probability that they are consecutive.
View SolutionThe odds in favour of an event are 3 : 4. Find the probability of :
(i) Occurrence (ii) Non-occurrence of the event.
View SolutionThree coins are tossed once. Find the probability of getting at least two tails.
View SolutionFind the probability distribution of the number of successes in two tosses of a die, where a success is defined as (i) number greater than 4 (ii) six appears on at least one die
View SolutionA random variable has the following distribution :
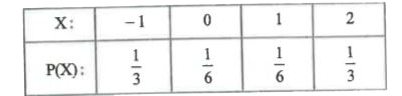
Does it represent a probability function ?
View SolutionFind mean `mu` for the following probability distribution :
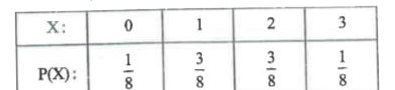
View SolutionFind the values of 'a' so that the following distribution is a probability distribution :

View SolutionFind E(X) from the adjoining probability distribution :

View Solution
Objective Type Question (D. Very Short Answer Tyep Questions) questions and complete solutions for chapter PROBABILITY of ARIHANT MATHS (HINGLISH) of Class 12
All Exercises from MODERN PUBLICATION Class 12 MATHS PROBABILITY
- CHAPTER TEST
- CHECK YOUR UNDERSTANDING
- COMPETITION FILE
- EXAMPLES
- Exercise
- EXERCISE 13 (a) (LATQ)
- EXERCISE 13 (a) (SATQ)
- EXERCISE 13 (b) (LATQ)
- EXERCISE 13 (b) (SATQ)
- EXERCISE 13 (c) (SATQ)
- EXERCISE 13 (d) (LATQ)
- EXERCISE 13 (e) (LATQ)
- EXERCISE 13 (e) (SATQ)
- EXERCISE 13 (f) (LATQ I)
- EXERCISE 13 (f) (LATQ II)
- EXERCISE 13 (f) (SATQ)
- EXERCISE 13 (g) (LATQ)
- EXERCISE 13 (g) (SATQ)
- EXERCISE 13 (h) (LATQ)
- Miscellaneous Exercise on Chapter 13
- MOCK TEST (Answer the following questions)
- MOCK TEST (Fill in the blanks)
- MOCK TEST (Select the correct option)
- MOCK TEST SECTION D
- NCERT-FILE (Exercise 13.1)
- NCERT-FILE (Exercise 13.2)
- NCERT-FILE (Exercise 13.3)
- NCERT-FILE (Exercise 13.4)
- NCERT-FILE (Exercise 13.5)
- Objective Type Question (A. Multiple Choice Questions)
- Objective Type Question (B. Fill in the Blanks)
- Objective Type Question (C. True/False Questions)
- Objective Type Question (D. Very Short Answer Tyep Questions)
- Revision Exercise