Complete Solutions to Revision Exercises (Long Answer ) of chapter ELECTRIC CHARGES AND FIELDS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTRIC CHARGES AND FIELDS |
| MODERN PUBLICATION | Revision Exercises (Long Answer ) |
| Number Of Questions | 15 |
| Academic Year | 2023-24 |
Why no two electric lines of force can interscet each other ?
View SolutionDefine electric dipole moment. Is it a scalar or a vector? Derive the expression for the electric field of a dipole at a point on the equatorial plane of the dipole.
View SolutionThe work in rotating electric dipole of dipole moment p in an electric field E through an angle `theta` from the direction of electric field, is:
View SolutionUse Gauss' law to derive the expression for the electric field `(vecE)` due to a straight uniformly charged infinite line of charge density `lambda C cdot m^(-1)`.
View SolutionThe maximum electric field intensity on the axis of a uniformly charged ring of charge q and radius R will be
View SolutionFind the expression of torque acting on an electric dipole placed in a uniform electric field . Using the above obtained expression of torque find the expression for potential energy of electric dipole kept in the uniform electric field . Assume potential energy of electric dipole to be zero when its axis is perpendicular to the externally applied electric field .
View SolutionAn isolated non-conducting solid sphere of radius R is given an electric charge. The charge is uniformly distributed in the volume of sphere. The graph which shows the correct variation of magnitude of electric field with distance from the centre of the sphere is
View SolutionState Gauss's law in electrostatics. Applying Gauss's law derive the expression for electric intensity due to an infinite plane sheet of charge.
View SolutionApplying Gauss's law derive the expression for electric intensity due to a charged conducting spherical shell at (i) a point outside the shell (ii) a point on the surface of the shell and (iii) a point inside the shell.
View SolutionA positive charge Q is situated at the centre of cube. The electric flux through any face of the cube is (in SI units)
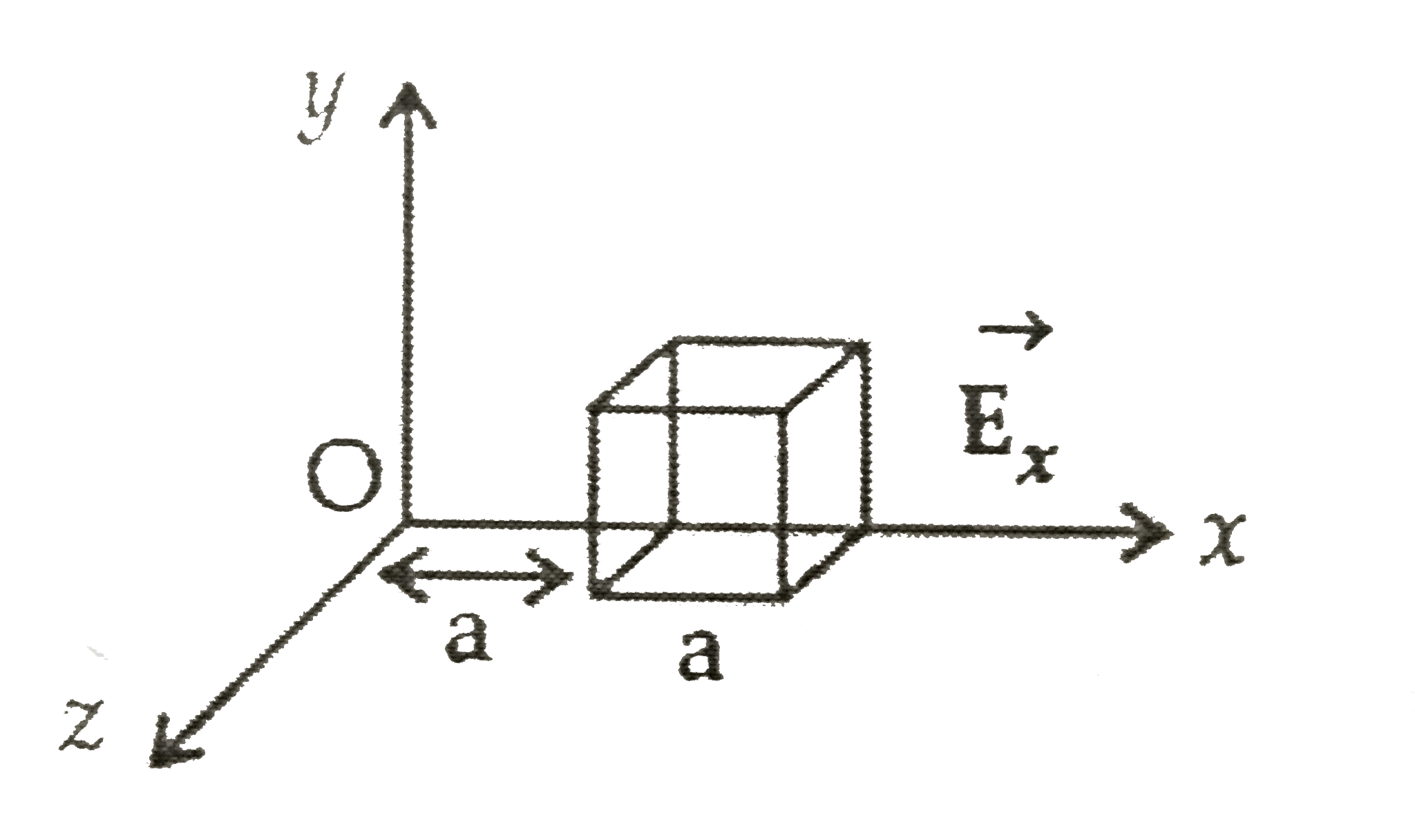
View SolutionIn Fig, electric field is directed along `+X` direction and is given by `E_(x) = 5 Ax + 2 B`, where E is in `NC^(-1)` and x is in meter, A and B are constants having dimensions. Taking `A = 10 NC^(-1) m^(-1) and B = 5 NC^(-1)`, calculate (i) the electric flux through the cube and (ii) net charge enclosed within the cube.
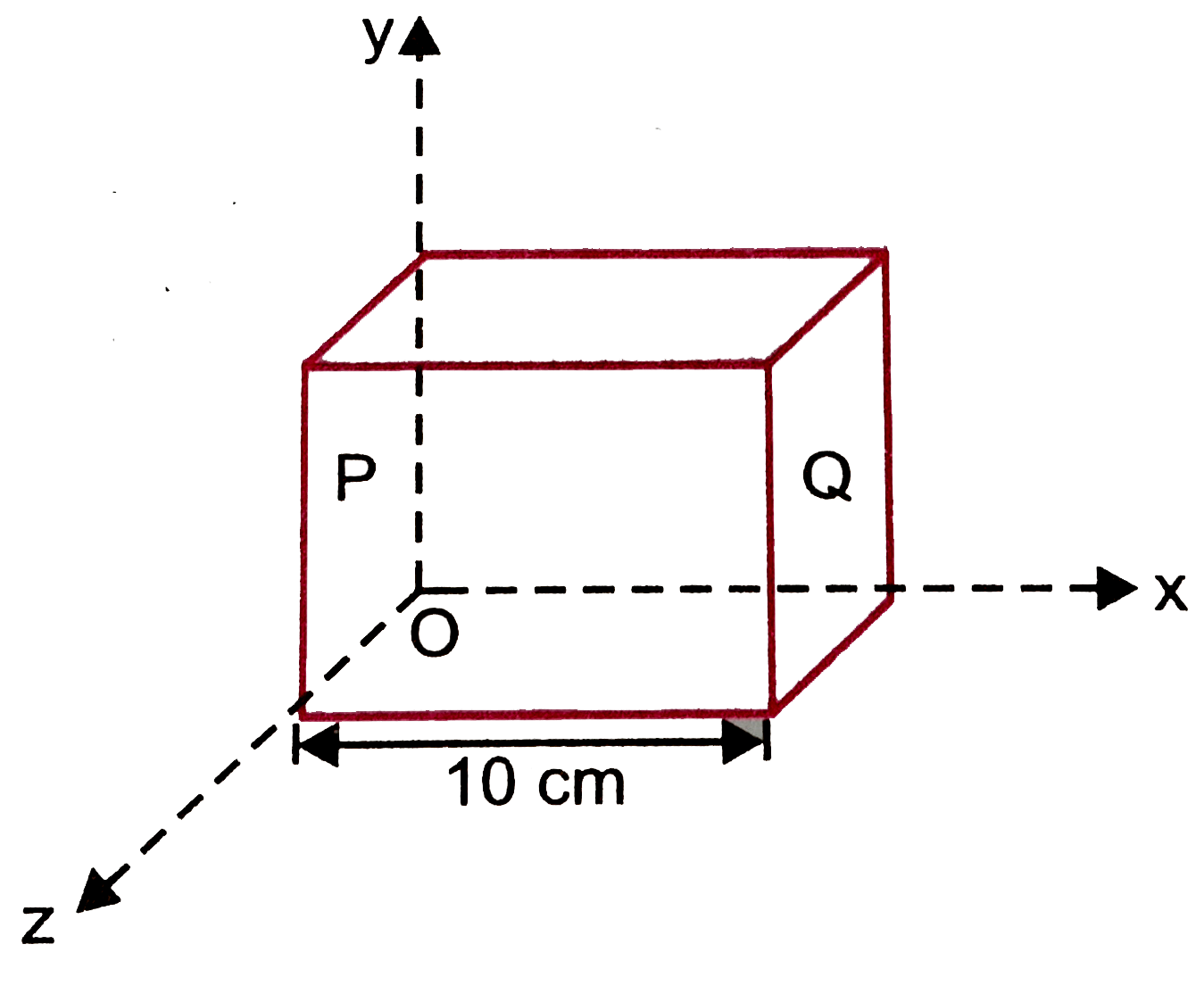
View SolutionDefine electric flux and write its SI unit . The electric field components in the figure shown are : `E_(x)=alphax,E_(y)=0,E_(z)=0` where `alpha=(100N)/(Cm)`.
Calculate the charge within the cube , assuming a = 0.1 m .
View SolutionUsing Gauss's law obtain the expression for the electric field due to uniformly charged thin spherical shell of radius R at a point outside the shell. Draw a graph showing the variation of electric tield with r, for r gt R and r lt R.
View Solution(a)An electric dipole of dipole moment `vecp` consists of point charges +q and -q separated by a distance 2a apart. Deduce the expression for the electric field due to the dipole at a distance x from the centre of the dipole on its axial line in terms of the dipole moment Hence show that in the limit:
r > > a, `vecE to (2vecp)/(4piepsilon_0r^3)`
(b) Given the electric field in the region `vecE=-2xhati`, find the net electric flux through the cube and the charge enclosed by it.

View SolutionDerive an expression for the electric field E due to a dipole of length 2a at a point at a distance r from the centre of the dipole on the axial line.
View Solution
Revision Exercises (Long Answer ) questions and complete solutions for chapter ELECTRIC CHARGES AND FIELDS of MODERN PUBLISHERS PHYSICS (HINGLISH) of Class 12
All Exercises from MODERN PUBLICATION Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS
- Chapter Practice Test
- COMPETITION FILE ( Objective Question (Assertion Reason ) )
- COMPETITION FILE ( Objective Question (BB.MCQ))
- COMPETITION FILE ( Objective Question (BC.MCQ))
- COMPETITION FILE ( Objective Question (C.MCQ))
- COMPETITION FILE ( Objective Question (D.MCQ) Passage )
- COMPETITION FILE ( Objective Question (A.MCQ) )
- COMPETITION FILE ( Objective Question (BA.MCQ) )
- COMPETITION FILE ( Objective Question (BA.MCQ))
- COMPETITION FILE ( Objective Question (Integer))
- COMPETITION FILE ( Objective Question (Matching ) )
- COMPETITION FILE ( Objective Question (Matrix))
- Conceptual Questions
- Higher Order Thinking Skills & Advanced Level (Questions With Answers)
- Ncert File (Ncert (Exemplar Problems) )
- Ncert File (Textbook Exercise)
- Practice Problems
- Revision Exercises (Additional Question)
- Revision Exercises (Fill in the Blanks )
- Revision Exercises (Long Answer )
- Revision Exercises (Numerical Problems )
- Revision Exercises (Short Answer )
- Revision Exercises (Very short)
- Solved Example
- Tough & Tricky Problems