Complete Solutions to Practice Problems of chapter ELECTRIC CHARGES AND FIELDS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTRIC CHARGES AND FIELDS |
| MODERN PUBLICATION | Practice Problems |
| Number Of Questions | 88 |
| Academic Year | 2023-24 |
A piece of woll is rubbed against a PVC strip. What will be the charge on the strip, if approximately `2xx10^12` electrons are transferred from the wool to the PVC strip ?
View SolutionFind the number of electrons present in an 8-g gold pin . Given : Molar mass of gold =197 g/mol , electron per atom is gold =79 and Avogadro's number `=6.023xx10^23 g^(-1) mol^(-1)`
View SolutionFind the total negative or positive charge on a 2 g silver coin. The atomic number and atomic mass of silver is 47 and 107.9 u respectively, Given: Avogadro's number is `6.023 xx 10^23 g^(-1) "mol"^(-1)` .
View SolutionFind the total negative and positive charges in 500 cc of water Given: Avogadro's number is `6.023 xx 10^(23) g^(-1)mol^(-1)`, molecular weight of water in 18.
View SolutionAn object with a net positive charge of `2 xx 10^(-12)` C contains `1.5 xx 10^7` protons. Calculate the number of electrons present on it.
View SolutionA Spherical ball is given one million electrons per second Calculate the time required by the ball to attain a charge of-0.8 C.
View SolutionAn object with an initial charge of 4 C is given `9 xx 10^19`additional electrons, Calculate the net charge on the object.
View SolutionA charged object having charge of-4C is given `9xx 10^19` electrons. Calculate the net charge on the object
View SolutionTwo spherical balls of the same radius carry charges -0.4 C and-0.9 C.Calculate the number of electrons to be transferred from one ball to another such that they attain the same charge
View SolutionCalculate the change in mass of an object if 800 electrons are given to it Given: Mass of an electron is `9.1xx10^(-31)` kg .
View SolutionThe charges on three dentical ebonite spheres are +2 mC, -4 mC and +2 mC respectively. Now the first sphere is brought in contact with the second sphere and then moved apart. Then, the second sphere is brought in contact with the third sphere and moved apart. Calculate the charge acquired by each sphere, provided ench sphere is kept on an insulated stand.
View SolutionThe identical anions are placed `7xx10^(-10)` m apart and experience of `4 xx 10^(-9)` N. Calculate the charge present on each anion
View SolutionTwo electrons are placed at a distance d such that electrostatic force between both the electrons is equal to sum of weight of both the electrons Calculate the value of d.
View SolutionTwo identical small plastic balls are rubbed against a piece of wool such that both of them received approximately `2 xx 10^12` and `2.5 xx 10^12` electrons respectively. Now both the charged balls are kept at a distance of 25 cm in air. Calculate the nature and magnitude of force between both the balls
View Solutioncalculate the change in electrostatic force between the two balls, if charge on both the balls are increased by 10%.
View SolutionTwo identical metallic balls with equal charges are kept 4.5 cm apart. The force between both the balls increases by 10% on giving extra charge of 0.001 `muC` to one of the ball. Calculate the charge on each ball.
View SolutionTwo small objects are rubbed against each other using insulating handles and then kept at a separation of 1 m from each other in vacuum. Both objects were found to attract each other with a force of 10 N. Assume that the force between the objects is of electrical nature. Calculate the number of electrons that were transferred from one object to another during the rubbing process.
View SolutionA point charge Q is kept fixed on a table and another particle of charge q and mass m is to be placed in air in such a way that it remains suspended at the same location in a state of equilibrium. What should be the distance of particle from point charge fixed on table?
View SolutionTotal charge Q is divided between two point objects in such a manner that electric force of repulsion between them is maximum when placed at a separation d from each other. What is the magnitude of this maximum possible electrostatic force between them?
View SolutionTwo point charges with charge magnitudes 2 nC and 3 nC are placed at a separation of 1 cm from each other and then released. The mass of each point charge is 1 `mu`g. Find the magnitude of acceleration of particles at the instant they are released.
View SolutionFour positive point charges Q are placed at the corners of a square of side a. Calculate the charge that should be placed at the centre so that system remains in equilibrium.
View SolutionThere is a particle A with positive charge `q_1` and mass m. There is another particle B with negative charge `q_2` and mass m. Particles A and B are moving along circular paths under electrostatic attraction in such a manner that separation between them is d and location of their centre of mass is centre of circular path. What will be the angular velocity of particles?
View SolutionTwo point charges Q are kept fixed on XY-plane at points A(0, d) and B(0, -d). Another point charge -q with mass m is held at a point, on the positive side of X-axis that is at the distance 2d from both the fixed point charges. What will be the magnitude of acceleration of the negative point charge (i) just after it is released from its location? (ii) at an instant it crosses the origin?
View Solutioncalculate the maximum possible force that the negative charge may experience if it is to be placed somewhere on X-axis, What will be the distance of negative charge from origin where it experiences the maximum electrostatic force?
View SolutionAssume an electron with charge e and mass m is going around in a circular path of radius r around the nucleus of an atom having atomic number Z. If we define frequency f for this electron equal to the number of revolution per second, then calculate f.
View SolutionThe ratio of magnitude of electrostatic force and gravitational force for an electron and a proton is
View SolutionTwo identical point charges q of mass m each are suspended through strings of equal length l from a common point of suspension. Find the charge q if angle subtended by the strings with the vertical is `theta`, when point charges are in a state of equilibrium.
View SolutionTwo particles of the same mass m are suspended through strings of equal length l in such a manner that points of suspension are distance d apart. Both particles carry charges of same magnitude but of opposite polarity. Calculate the magnitude of charge if strings make an angle `theta` with the vertical.
View SolutionTwo charges of 2 mC and 8 mC are kept at (2 m,0) and (7 m, 0) respectively. At what position, a third charge Q should be kept so that all the three charges are in equilibrium. Also calculate the magnitude of charge Q.
View SolutionThree identical charges of 2mC are kept on the vertices of an equilateral triangle of side 10 cm. A third charge of 1 mC is kept on the centroid of the triangle Calculate the force acting on the charge 1mC.
View SolutionThree charges of 2 mC, -4 mC and -4mC are placed on the vertices of an equilateral triangle of side 10 cm. A charge q is kept on the midpoint between both -4mC charge. Calculate the value of q such that the 2 mC charge remains at equilibrium.
View SolutionTwo point charges `-2muC` and `+3muC` are kept r distance apart. The `+3muC` charge is displaced such that the force of attraction between both the charges is now tripled. Calculate the final distance between both the charges.
View SolutionTwo identical charge of magnitude +2 `muC`are kept on two diagonally opposite vertices of a square of side a. Both the charges are joined using an insulated massless chord. What will be the tension in the chord? Neglect the gravitational forces involved.
View SolutionTwo identical charges of `1muC` are kept on 0,2 m) and (0,-2 m), respectively. Calculate the magnitude of the force acting on a `2muC` charge placed at (-5m,0).
View SolutionTwo charges `+0.4 muC` and`-0.2 muC` are placed on adjacent vertices of a square of side 10 cm. Another charge of `1.2muC` is placed at the centre af the square Calculate the force and its direction in the charge kept in the centre .
View SolutionArrange three point charges `2muC, 4muC` and `1mu C` on a straight line segment of 1 m such that net force experienced by the `1muC` charge is zero
View SolutionAn electron is moving in an orbit in hydrogen atom of radius `0.5xx 10^(-10)` m. Calculate the time period of electron about the nucleus
View SolutionDistributed charge of 1 C into two parts such that these part a experience the maximum force when they are kept at a distance of 1 km.
View SolutionFifty charged particles of magnitudes `0.01 muC, 0.04 muC , 0.09 muC` ….and so on are placed at points (0.1 m), (0.2 m), (0.3 m) ........ respectively What will be the force acting on charge of 0.1 `muC` placed at (0,0)
View SolutionCharged particles of charge 0.001 `mu`C are placed on Y-axis at points (0,1 m) (0,2 m),( 0.3 m) and so on till infinity. Find the net force on charge of 0.1`muC` placed at (0,0).
View SolutionTwo small identical balls, each of mass 0.20 g, carry identical charges and are suspended by two threads of equal lengths. The balls position themselves at equilibirum such that the angle between the threads is `60^(@)`. If the distance between the balls is 0.5 m, find the charge on each ball.
View SolutionA glycerin drop of mass `10^(-3)` g with charge equal to 2e is balanced in an external electric field. Calculate the strength of electric field, if the field is sufficient enough to hold the drop.
View SolutionA small metallic ball with charge 1 `mu`C and mass 0.1 mg, when thrown in an upward direction with initial velocity u, comes to rest after covering a distance of 5 cm in a uniform external electric field of strength `2.8xx10^6 NC^(-1)` . Find the value of u.
View SolutionIn Millikan's oil drop experiment, an oil drop with density `1.5 g cm^(-3)` and a radius of `10 xx 10^(-7)` m is supported by an external electric field. Calculate the required electric field strength if charge on the drop is 15e.
View SolutionA small metallic sphere with charge 0.1 `mu`C is suspended by an insulating massless string in a region of electric field of strength 500 `NC^(-1)`. Calculate the tension in the string if mass of the sphere is 0.8 grams and the electric field is directed in a downward direction.
View Solutioncalculate the tension in the string and angle made by it with vertical if electric field is directed in horizontal direction.
View SolutionA small particle of mass `1.8 xx 10^(-30)` kg and charge `-3.5 xx 10^(-19)` C is dropped in a region of electric field of strength `2.8 xx 10^5 NC^(-1)`, directed in the upward direction. Calculate the time taken by the ball to cover a distance of 2 cm.
View Solutioncalculate the time taken by a spherical ball if the direction of electric field is reversed and the charge on the particle is changed to `+3.5xx10^(-19)` C
View SolutionA point charge of 0.01 `mu`C is placed at the origin. Calculate the electric field at another point charge of 0.05 `mu`C placed at (0 m, 5 m).
View SolutionTwo point charges of, 1 `mu`C and -1 `mu`C are kept at (-2 m, 0) and (2 m, 0) respectively. Calculate the electric field at point (0, 5 m).
View Solutioncalculate the electric field at point (5 m, 0) due to a point charge of 1 x 10(-6) C placed at (0,5m).
View SolutionTwo point charges of magnitude 4 `mu`C and-4`mu`C are kept at points (-2 cm, 0) and (2 cm, 0) respectively. Calculate the magnitude of electric field intensity at points (0, 2 cm).
View SolutionElectric force experienced by a charge of `1 muC` is `5 xx 10^(-3)` N. What should be the magnitude of electric field intensity at the position of the charge?
View SolutionThe magnitude of electric field intensity due to a point charge is 10 N/C at a distance 1 m from it. Calculate the magnitude of charge.
View SolutionTwo point charges `q_1` and `q_2` are fixed at a separation of 20 cm. Locate the point(s) on the line joining the charges where the net electric field intensity is zero.
(i)`q_1=+2muC` and `q_2=-4 muC`
(ii)`q_1=+2muC` and `q_2=-2muC`
(iii)`q_1=+2muC` and `q_2=+4muC`
View SolutionA particle of mass 1 mg loses 108 electrons and then stays in equilibrium against gravity inside electric field. What should be the magnitude and direction of the electric field intensity?
View SolutionA very small particle of mass m and charge q is given an initial speed u against uniform electric field E. How much distance will the particle cover before acquiring the same speed again?
View SolutionA small ball of mass m and charge q is suspended through a string in uniform electric field E applied in horizontal direction. How much tension would be developed in the string if it stays in equilibrium?
View SolutionA charged particle of mass `m` and charge `q` is released from rest in an electric field of constant magnitude `E`. The kinetic energy of the particle after time `t` is
View SolutionMass of bob of a pendulum is m and it is suspended from the ceiling inside a uniform external electric field of magnitude E directed in horizontal direction. Initially the bob has no charge and it takes time T to complete one oscillation. Now it is given a positive charge q. How much time will the bob take to complete one oscillation now?
View SolutionA block of mass m is placed on a frictionless horizontal table. Consider a spring of spring constant K whose one end is connected to the block and the other end is connected to a fixed support in such a manner that spring remains horizontal. A positive charge q is given to the block. Suddenly an electric field of magnitude E is switched on in horizontal direction that is in the direction away from the fixed support. What will be the maximum possible elongation of the spring after electric field is switched on?
View SolutionA charge `+q` is placed at a distance 'd' from the centre of the uncharged metallic cube of side 'a'. The electric field at the centre of the cube due to induced charges on the cube will be
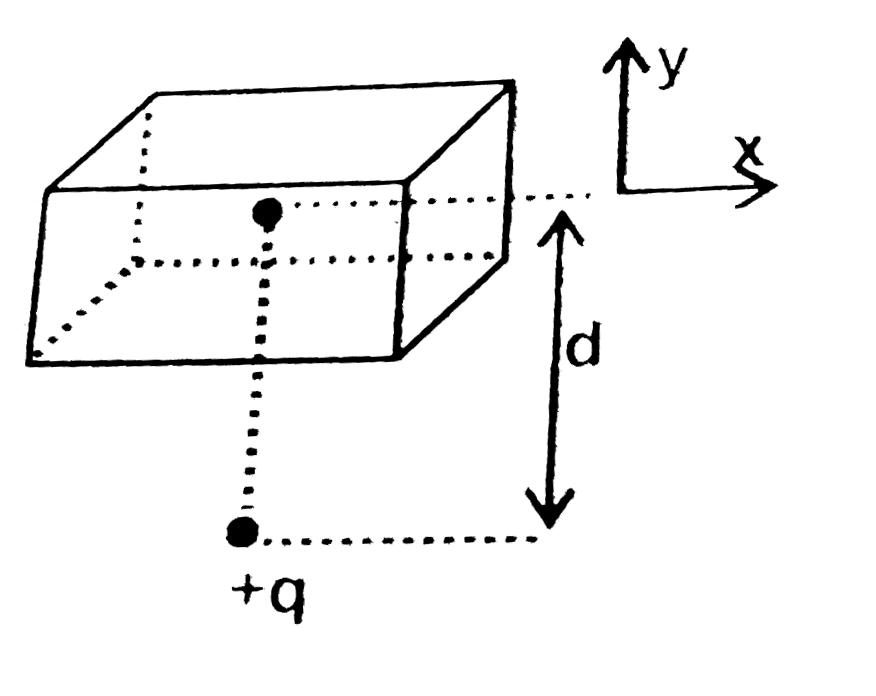
View SolutionThere is one charged tiny spherical oil drop and the magnitude of electric field intensity at a point on its surface is E. If n such drops are combined to make a single drop then what will be the net electric field intensity at a point on the surface of the bigger spherical drop. Assume that charge is uniformly distributed over the volume of oil drop.
View SolutionA tiny spherical oil drop carrying a net charge q is balanced in still air with a vertical uniform electric field of strength `(81pi)/(7)xx10^5Vm^-1`. When the field is switched off, the drop is observed to fall with terminal velocity `2xx10^-3ms^-1`. Given `g=9.8ms^-2`, viscoisty of the air `=1.8xx10^-5Nsm^-2` and the denisty of oil `=900kg m^-3`, the magnitude of q is
View SolutionAn electric dipole consists of two charges of `pm0.5 muC`, kept at distance of 1.0 cm. Calculate the potential energy required to place the dipole such that it makes an angle of `30^@` with the external electric field of `0.8 xx 10^4` N/C.
View SolutionTwo charged particles of charges +0.1 `mu`C and -0.1 `mu`C are kept on the vertices of an equilateral triangle of side 10 cm. Calculate the electric field intensity at the centroid of the triangle.
View SolutionFour point charges, +0.1 `mu`C,-0.1 `mu`C,-0.1 `mu`C and +0.1 `mu`C are kept at points A(0, 2 m), B(0, -2 m), C (-`sqrt2` m, `sqrt2` m) and D (`sqrt2` m, -`sqrt2` m) respectively. Calculate the resultant dipole moment of the combination.
View Solutioncalculate the magnitude and direction of the torque acting on the combination, if it is placed in an external electric field of `10^(4) NC^(-1)` directed along X-axis.
View SolutionSix point charges are arrange at the vertices of a regular hexagon of side length a (shown in figure).
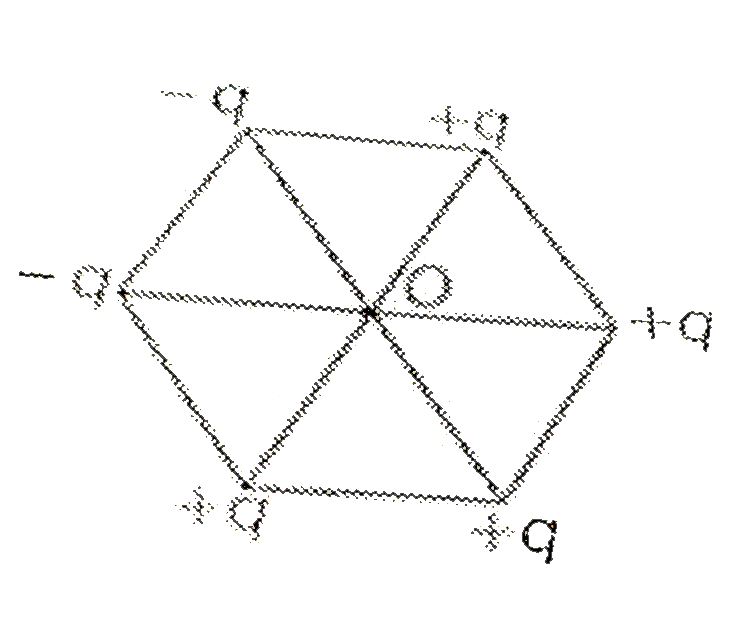
Find the magnitude of electric field at the centre of regular hexagon.
View SolutionCalculate the magnitude of electric field at the centre of a regular hexagon of side 2.5 cm, if each charge placed at its vertex has the same magnitude of +0.01 `mu`C.
View SolutionCalculate the electric field at the centre of a cube, if seven of its corners are given a charge of 0.02 `mu`C and side of cube is 10 mm.
View SolutionA proton is placed at a distance of `3 xx 10^(-9)` m from the centre of an electric dipole along the axis of the dipole. Calculate the force on the proton due to dipole if its dipole moment is `4 xx 10^(-30)` C m. Given: Dipole length < < `3xx10^(-9)` m.
View SolutionTwo point charges +4 `mu`C and -4 `mu`C are place(at vertices P and Q respectively of a right angled triangle. Calculate the magnitude and direction of electric field at a point R, if `anglePQR = 90^@`, PQ =0.03 cm and QR = 0.04 cm.
View SolutionAn electric dipole experiences a torque of `10sqrt3` Nm, when placed at an angle of `60^@` with a uniform electric field of magnitude `10^3 NC^(-1)` Calculate the charge on the dipole if its length is 3 cm.
View SolutionA positive charge Q is uniformly distributed across a rod of length L. The rod is then bent in the form of a semicircle. What will be the electric field intensity at the centre of curvature of the semicircle thus formed?
View SolutionFind the electric field intensity at the centre of a semi circular arc of radius r, uniformaly charged with a charge q.
View SolutionConsider a uniformly charged ring of radius R and total charge Q. What is the magnitude of maximum possible electric field intensity on the axis of ring? What is the distance of point from the centre of ring at which the electric field is maximum?
View SolutionA rod of length 20 cm carries a charge of +150 `mu`C that is uniformly distributed along its length. Find the electric field intensity at a point, which is 20 cm away from both the ends of the rod.
View SolutionA positive charge Q is uniformly distributed along the length L of a rod. It is bent in the shape of a square. Calculate electric field intensity at the centre of the square.
View SolutionConsider one design of electron gun, which has a barrel of length 1 m made of an insulating material. At one end of the barrel, a filament is electrically heated so that it emits electrons. Assume these electrons are emitted with a the sides negligible speed. What electric field should be applied parallel to the barrel so that electrons may achieve speed of light before leaving the barrel? Ignore the variation of mass of electron due to its speed.
View SolutionA charge q is uniformly distributed over a large plastic plate. The electric field at a point P close to the centre and just above the surface of the plate is 50 V/m. If the plastic plate is replaced by a copper plate of the same geometrical dimensions and carrying the same uniform charge q, the electric field at the point P will become :
View SolutionA point charge Q is kept at the centre of a square face of edge length a. Calculate the amount of flux linked with the square face due to electric field of given point charge.
View SolutionA sphere of radius R has a charge density `sigma`. The electric intensity at a point at a distance r from its centre is
View SolutionThere is one large vertical non-conducting plane surface with uniformly distributed charge. A pendulum bob is suspended through an insulating string from a point on this non-conducting surface. The length of the string is l and mass of the bob is m. The charge carried by the pendulum bob is q. It is found that in a state of equilibrium, the string of the pendulum makes `60^@` angle with the vertical. What will be the charge per unit area on surface? Also calculate the tension developed in the string in equilibrium state.
View SolutionTwo large conducting plates are placed parallel to each other with a separation `d`. An electron `(-e ,m)` starting from rest near one of the plates reaches the other plate in time `t_(0)`. Find the surface density on the inner surface.
View SolutionCalculate the magnitude of electric field intensity at a point 10 cm away from a line charge of linear charge density 5 `mu`C/m.
View SolutionWhat magnitude of force will be applied by a `2 muC` point charge on a large non- conducting surface having surface charge density of `6 muC//m^2` placed near it?
View SolutionA Uniformly charged solid non-conducting sphere of uniform volume charge density `rho` and radius R is having a concentric spherical cavity of radius r. Find out electric field intensity at following points, as shown in the figure :

(i) Point A (ii) Point B
(iii) Point C (iv) Centre of the sphere
View Solution
Practice Problems questions and complete solutions for chapter ELECTRIC CHARGES AND FIELDS of MODERN PUBLISHERS PHYSICS (HINGLISH) of Class 12
All Exercises from MODERN PUBLICATION Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS
- Chapter Practice Test
- COMPETITION FILE ( Objective Question (Assertion Reason ) )
- COMPETITION FILE ( Objective Question (BB.MCQ))
- COMPETITION FILE ( Objective Question (BC.MCQ))
- COMPETITION FILE ( Objective Question (C.MCQ))
- COMPETITION FILE ( Objective Question (D.MCQ) Passage )
- COMPETITION FILE ( Objective Question (A.MCQ) )
- COMPETITION FILE ( Objective Question (BA.MCQ) )
- COMPETITION FILE ( Objective Question (BA.MCQ))
- COMPETITION FILE ( Objective Question (Integer))
- COMPETITION FILE ( Objective Question (Matching ) )
- COMPETITION FILE ( Objective Question (Matrix))
- Conceptual Questions
- Higher Order Thinking Skills & Advanced Level (Questions With Answers)
- Ncert File (Ncert (Exemplar Problems) )
- Ncert File (Textbook Exercise)
- Practice Problems
- Revision Exercises (Additional Question)
- Revision Exercises (Fill in the Blanks )
- Revision Exercises (Long Answer )
- Revision Exercises (Numerical Problems )
- Revision Exercises (Short Answer )
- Revision Exercises (Very short)
- Solved Example
- Tough & Tricky Problems