Complete Solutions to NCERT FILE Solved (Additional Exercises) of chapter ELECTROSTATIC POTENTIAL AND CAPACITANCE of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTROSTATIC POTENTIAL AND CAPACITANCE |
| MODERN PUBLICATION | NCERT FILE Solved (Additional Exercises) |
| Number Of Questions | 23 |
| Academic Year | 2023-24 |
A charge of 8 mC is located at the origin. Calculate the work done in taking a small charge of `-2xx10^(-9)C` from a point P (0,0,3 cm) to a point Q (0,4 cm, 0) via a point R (0,6 cm, 9cm).
View SolutionA cube of side b has a charge q at each of its vertices. Determine the potential and electric field due to this charge array at the center of the cube.
View SolutionTwo tiny spheres carrying charges `1.5 muC` and `2.5 muC` are located 30 cm apart. Find the potential
(a) at the mid-point of the line joining the two charges and
(b). At a point 10 cm from this mid-point in a plane normal to the line and passing through the mid-point.
View SolutionA spherical conducting shell of inner radius `r_(1)` and outer radius `r_(2)` has a charge Q:
(a) A charge q is placed at the centre of the shell. What is the surface charge density on the inner and outer surfaces of the shell?
(b) Is the electric field inside a cavity (with no charge) zero even if the shell is not spherical, but has any irregular shape? Explain.
View Solution(a) Show that the normal component of electrostatic field has a discontinuity from one side of a charged surface to another given by:
`(vecE_(2)-vecE_(1)). hatn =(sigma)/(epsilon_(0))`
where `hatn` is a unit vector normal to the surface of a point and `sigma` is the surface charge density at that point. (The direction of `hatn` is from side 1 to side 2). Hence, show that just outside a conductor, the electric field is `(sigma hatn)/(epsilon_(0))`.
(b) Show that the tangential component of electrostatic field is continuous from one side of a charged surface to another.
View SolutionA long charged cylinder of linear charge density `lambda` surrounded by a hollow co-axial conducting cylinder. What is the electric field in the space between the two cylinders?
View SolutionIn a hydrogen atom, the electron and proton are bound at a distance of about 0.53 Å:
(a) Estimate the potential energy of the system in eV, taking the zero of the potential energy at infinite separation of the electron from proton.
(b) What is the minimum work required to free the electron, given that its kinetic energy in the orbit is half the magnitude of potential energy obtained in (a)?
(c) What are the answers to (a) and (b) above if the zero of potential energy is taken at 1.06 Å separation?
View SolutionIf one of the two electrons of a `H_(2)` molecule is removed, we get a hydrogen molecular ion `(H_(2)^(+))`. In the ground state of an `(H_(2)^(+))`, two protons are separated by roughly 1.5 Å and the electron is roughly 1 Å from each proton. Determine the potential energy of the system. Specify your choice of the zero of potential energy.
View SolutionTwo charged conducting spheres of radii a and b are connected to each other by a wire. What is the ratio of electric fields at the surface of two spheres ? Use the result obtained to explain why charge density on the sharp and pointed ends of a conductor is higher than on its fatter portions ?
View SolutionTwo charges -q and +q are located at points (0, 0, –a) and (0, 0, a), respectively.
(a) What is the electrostatic potential at the points (0, 0, z) and (x, y, 0) ? (b) Obtain the dependence of potential on the distance r of a point from the origin when `r//a gt gt 1`.
(c) How much work is done in moving a small test charge from the point (5,0,0) to (–7,0,0) along the x-axis? Does the answer change if the path of the test charge between the same points is not along the x-axis?
View SolutionThe figure given below shows a charge array known as an 'electric quadrupole'. For a point on the axis of the quadrupole, obtain the dependence of potential on r for `(r )/(a) gt gt 1`. Contrast your result with that due to an electric dipole and an electric monopole (i.e. a single charge).

View SolutionAn electrical technician requires a capacitance of `2 muF` in a circuit across a potential difference of 1 kV. A large number of `1 mu F` capacitors are available to him each of which can withstand a potential difference of not more than 400 V. Suggest a possible arrangement that requires the minimum number of capacitors.
View SolutionWhat is the area of the plates of a 2 F parallel plate capacitor , given that the separation between the plates is 0.5cm ? [You will realise from your answer why ordinary capacitors are in the range of `muF` or less. However , electrolytic capacitors do have a much larger capacitance `(0.1F)` because of very minute separation between the conductors.]
View SolutionObtain the equivalent capacitance of the network in Fig. For a 300 V supply. Determin the change and voltage across each capacitor.
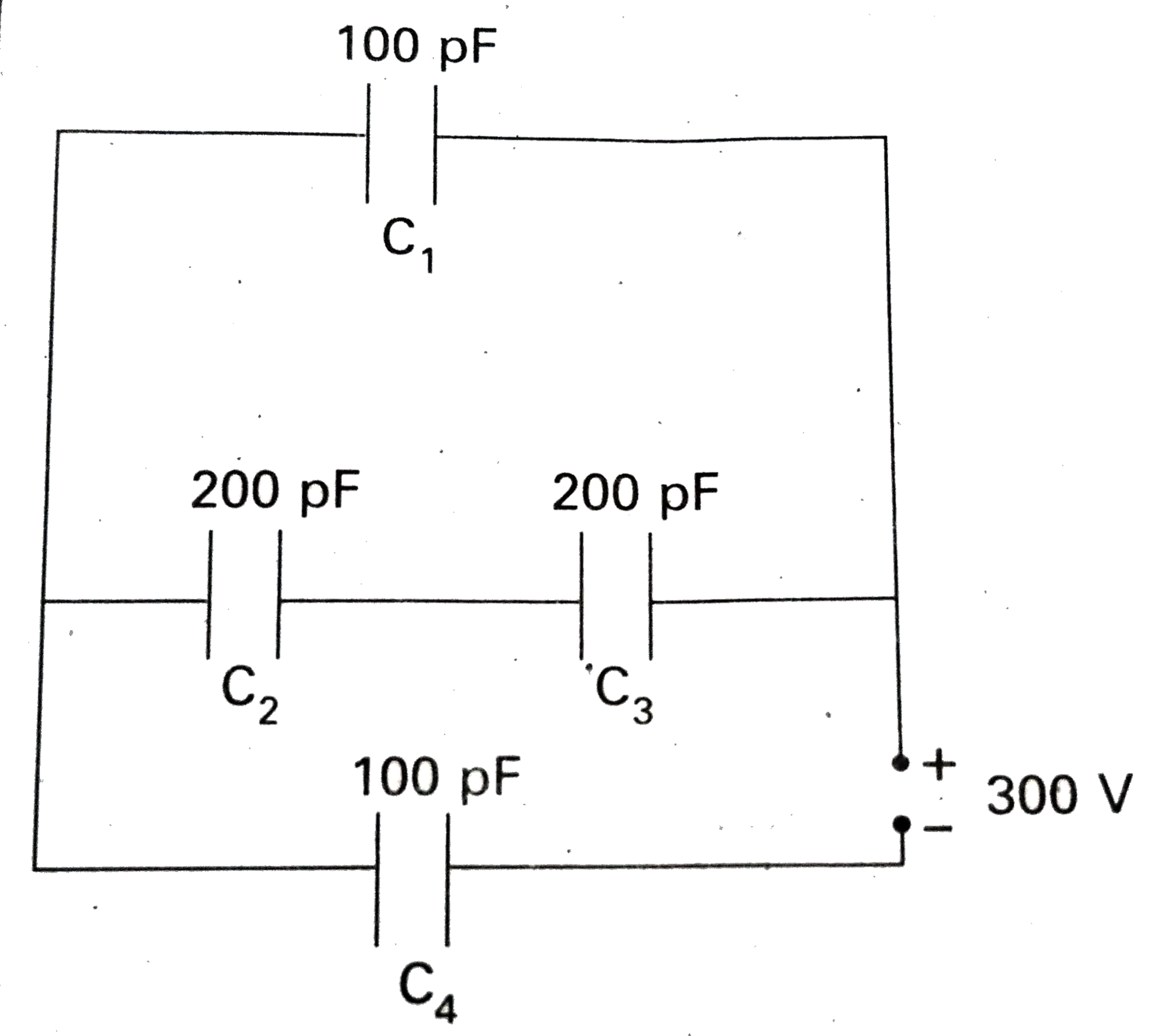
View SolutionThe plates of a paralllel plate capacitor have an area of `90 cm^(2)` each and are separated by 2.5mm. The capacitance is charged by connecting it to a 400V supply.
(a) How much electrostatic energy is stored by the capacitor ?
(b) View this energy as stored in the electrostatic field between the plates, and obtain the energy per unit volume (u). Hence arrive at a relation between U and the magnitude of electric field E between the plates.
View SolutionA `4 muF` capacitor is charged by a 200 V supply. It is then disconnected from the supply and is connected to another uncharged `2 mu F` capacitor. How much electrostatic energy of the first capacitor is disspated in the form of heat and electromagnetic radiation ?
View SolutionShow that the force on each plate of a parallel plate capacitor has a magnitude equal to `(½) QE`, where Q is the charge on the capacitor, and E is the magnitude of electric field between the plates. Explain the origin of the factor `½`.
View SolutionA spherical capacitor consists of two concentric spherical conductors, held in position by suitable insulating supports (Fig). Show that the capacitance of a spherical capacitor is given by `C=(4piepsi_0r_1r_2)/(r_1-r_2)`

where `r_1 and r_2` are the radii of outer and inner spheres , respectively.
View SolutionA spherical capacitor has an inner sphere of radius 12 cm and an outer sphere of radius 13 cm. The outer sphere is earthed and the inner sphere is given a charge of `2.5 muC`. The space between the concentric spheres is filled with a liquid of dielectric constant 32.
(a) Determine the capacitance of the capacitor. (b) What is the potential of the inner sphere ?
(c) Compare the capacitance of this capacitor with that of an isolated sphere of radius 12 cm.Explain why the later is much smaller ?
View SolutionA cylindrical capacitor has two co-axial cylinders of length 15 cm and radil 1.5 and 1.4 cm.The outer cylinder is earthed and inner cylinder is given a charge of `3.5 muC`. Determine the capacitance of the system and the potential of the inner cylinder. Neglect end effects (i.e., bending of field lines at the ends.)
View SolutionA parallel plate capacitor is to be designed with a voltage rating 1 KV using a material of dielectrical constant 3 and dielectric strength about `10^(7) Vm^(-1)`. [Dielectric strength is the maximum electric field a material can tolerate without break down, i.e, without starting to conduct electrically through partial ionisation. For safety, we should like the field never to exceed say `10%` of the dielectric strength]. What minimum area of the plates is required to have a capacitance of 50 pF ?
View SolutionDescribe schematically the equipotential surfaces corresponding to
(a) a constant electric field in the z-direction,
(b) a field that uniformly increases in magnitude but remains in a constant (say, z) direction,
(c) a single positive charge at the origin, and
(d) a uniform grid consisting of long equally spaced parallel charged wires in a plane.
View SolutionA small sphere of radius `r_(1)` and charge `q_(1)` is enclosed by a spherical shell of radius `r_(2)` and charge `q_(2)`. Show that if `q_(1)` is positive, charge will necessarily flow from the sphere to the shell (when the two are connected by a wire) no matter what the charge `q_(2)` on the shell is [Fig]
View Solution
NCERT FILE Solved (Additional Exercises) questions and complete solutions for chapter ELECTROSTATIC POTENTIAL AND CAPACITANCE of MODERN PUBLISHERS PHYSICS (HINGLISH) of Class 12
All Exercises from MODERN PUBLICATION Class 12 PHYSICS ELECTROSTATIC POTENTIAL AND CAPACITANCE
- Chapter Practice Test
- Competition file (ASSERTION REASON TYPE QUESTIONS)
- Competition file (INTEGER TYPE QUESTIONS)
- Competition file (MATCHING TYPE QUESTIONS)
- Competition file (MATRIX TYPE QUESTIONS)
- Competition file (MULTIPLE CHOICE QUESTIONS based on a given passage/comprehension)
- Competition file (NCERT Exemplar Problems: Multiple Choice Questions Type-I)
- Competition file (NCERT Exemplar Problems: Multiple Choice Questions Type-II)
- Conceptual Questions
- Higher Order Thinking Skills & Advanced Level (QUESTIONS WITH ANSWERS)
- NCERT FILE Solved (Additional Exercises)
- NCERT FILE Solved (Additional Exercises) (Answer carefully)
- NCERT FILE Solved (Additional Exercises) (Answer the following)
- NCERT FILE Solved (Exemplar Problems) (Short Answer Type Questions)
- NCERT FILE Solved (Exemplar Problems) (Very Short Answer Type Questions)
- NCERT FILE Solved (Textbook Exercise)
- PRACTICE PROBLEMS 1
- PRACTICE PROBLEMS 2
- PRACTICE PROBLEMS 3
- PRACTICE PROBLEMS 4
- PRACTICE PROBLEMS 5
- Revision Exercises (Additional Questions)
- Revision Exercises (Fill in the Blanks)
- Revision Exercises (Long Answer Questions)
- Revision Exercises (Numerical Problems)
- Revision Exercises (Short Answer Questions)
- Revision Exercises (Very Short Answer Questions)
- SOLVED EXAMPLES
- Tough & Tricky PROBLEMS