Complete Solutions to SOLVED EXAMPLES of chapter ELECTROSTATIC POTENTIAL AND CAPACITANCE of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTROSTATIC POTENTIAL AND CAPACITANCE |
| MODERN PUBLICATION | SOLVED EXAMPLES |
| Number Of Questions | 47 |
| Academic Year | 2023-24 |
Two electrons are fired towards each other with a speed of `3xx10^(6)` m/s. What would be the minimum separation between the electrons?
View SolutionTwo point objects of masses 10 g each carry charges of opposite nature with the same magnitude of 50 `muC` are held at rest at a separation of 2 m. Now the point objects are released from the state of rest. Calculate the speed acquired by both the objects when separation between them reduces to half of the initial value.
View SolutionTwo point charges 9 `muC` and `-2muC` are placed at a separation of 20 cm from each other.
(i) Calculate the electric potential energy of this system of two charges.
(ii) What amount of work is required to separate the particles to infinite separation?
View SolutionOne insulated metal sphere is charged to a potential of `3xx10^(5)` Volts. What should be the radius of the sphere so that it may cause breakdown in air? Dielectric strength of air is `3xx10^(6)V//m`.
View SolutionTwo point charges 2 `muC` and 0.1 `muC` are held at a separation of 20 mm. What work is required by the external agent to move the charges to half of the given separation?
View SolutionTwo electrons are held at some separation. A third charge q is to be placed at the midpoint between these two electrons. What should q be so that electric potential energy of the system becomes zero?
View SolutionThree point charges are arranged at the vertices of an equilateral triangle ABC of side l. Charges at A, B and C are +q, +4q and -6q, respectively.
(i) Calculate electric potential energy of this system.
(ii) Charge at A is moved to the midpoint of AB, charge at B is moved to midpoint of BC and charge at C is moved to midpoint of CA. Calculate electric potential energy of this system now.
(iii) What work is needed to shift the charges to new locations as described in part (ii)?
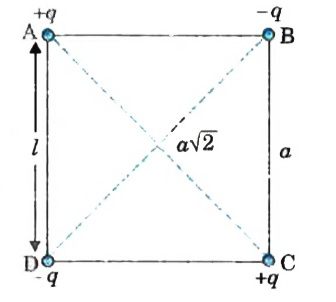
View SolutionTwo point charges of +q each are placed at two diagonally opposite corners of a square. Another two point charges of -q charge each are placed at the two remaining corners. Take the edge length of square equal to l. Calculate (i) work needed to move these charges slowly from an infinite separation to this given configuration. (ii) Assume that four charges at corners of the square are held fixed. Another charge Q is to be moved from infinity to the centre of this square slowly. What additional work is required to do so?
View SolutionConsider an x-y plane and mark the locations A, B and C whose coordinates are given to be (5, 2), (5, 8) and (-5, 8) respectively. A uniform electric field of 200 N/C exists in space directed along the negative x-direction. Calculate `(i) V_(B)-V_(A) (ii) V_(C )-V_(A) (iii) V_(B)-V_(C )`.
View SolutionA uniform electric field E exists in a region of space. Refer to the given figure for the location of three points A, B and C.
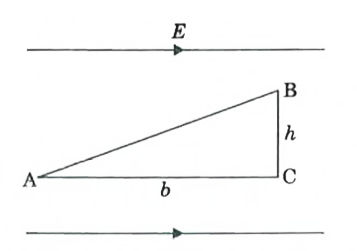
Find: `(a) V_(B)-V_(A)" " (b) V_(C )-V_(A)`
View SolutionA uniform electric field of 2,000 N/C exists in space. Consider a right angled triangle `DeltaABC` such that `angleABC` is a right angle. Edge AB of the triangle is kept parallel to electric field. Edge AB is 3cm long and edge BC is 4cm long. Calculate potential difference `V_(A)-V_(C )`. Is the answer affected by the orientation of triangle inside field keeping edge AB parallel to the field?
View SolutionThe magnitude of electric field intensity and electric potential due to a point charge at a point is 72 N/C and 36V, respectively. Calculate magnitude of the charge and distance of the point from point charge.
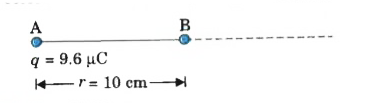
View SolutionA point charge of 9.6 `muC` is placed at a point A. Point B is at a distance of 10 cm from A. (i) Calculate electric potential at point B due to charge at A. (ii) If a point charge of 3 nC is brought from infinity to the point B, then calculate work done by the external agent in this process assuming motion of charge to be slow.
View SolutionPoint charges of 9 `muC and -6muC` are placed at a distance of 90 cm from each other. How many points can you find on line joining the charges where electric potential is zero? At what distance these these points are located from 9 `muC`?
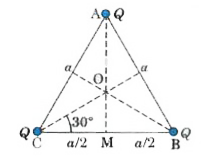
View SolutionThree identical point charges Q are placed at the three corners of an equilateral triangle of side length a. Find the electric potential at points O and M due to the three charges.
View SolutionThere is a, and four charges +q, +q, -q and -q are fixed at the four corners of square. See the figure for the placement of charges.
Calculate:
(i) Electric potential at point O.
(ii) Work done to move a charge +e from point O to point B.
(iii) Work done to move a charge +e from point O to A.

View SolutionLet there be a short dipole having dipole moment of `5xx10^(-8)` Cm. Calculate electric potential due to this dipole at point which is 1 m away from the centre of dipole in the following cases: (i) the point is on the axis of dipole (ii) the point is on the equatorial plane of dipole (iii) the point is on a line at an angle `60^(@)` with the axis and passing through the centre.
View SolutionAn electric dipole is constructed using equal and opposite charges of magnitude 10 `muC` and placing them at a separation 1 mm. There is a point P at a distance 1 m from the centre of dipole. (i) Calculate electric field intensity and potential at point P. (ii) What will be the answers to the part. (i) if electric dipole is turned through right angle from its existing orientation?
View SolutionElectric potential in a region of space is given by `V=3x^(2)V`. What will be electric field intensity at a point P (2 m, 0).
View SolutionElectric potential in a region of space is given by `V=(x^(2)+y^(2)+z^(2))V`. What will be electric field intensity at a point P(-1m, 2m, -3m)?
View SolutionElectric field intensity in a region of space is given by `vecE=10x^(2)hati N//C`. What will be potential difference between point A(2, 5) and B(-1, 10)?
View SolutionElectric potential in a region is given by `V=12x^(2)+3y^(2)+z^(2)`. Calculate the electric field intensity at point (1m, 3m, 2m).
View SolutionA charge of 500 `muC` is distributed uniformly over the circumference of a ring of radius 25 cm. What will be be electric potential at the centre of ring?
View SolutionThe surface charege density for a spherical conductor is `2muC//m^(2)`. Calculate electric potential of the conductor, assuming its radius to be 0.2 m.
View SolutionAssume that total positive charge of gold nucleus (atomic number, Z = 79) is distributed uniformly in a spherical region of radius `9.6xx10^(-15)m`. Calculate electric potential at the surface of this sphere.
View SolutionA charge of 108 `muC` is given to a metallic spherical shell of radius1 m. (i) Calculate electric potential at the surface of the shell. (ii) Calculate electric potential at a point that is 0.1 m from the centre of the shell.
View SolutionThere are 64 drops charged to a potential 100 volts each. These drops combine to form a bigger drop. Calculate electric potential at the surface of bigger drop.
View SolutionA uniformly charged solid (non-conducting) sphere of radius R carrying positive charge, has a volume charge density equal to `rho`. A tunnel of very small radius is made along the diameter of the sphere. A particle of mass m and charge -q is released from rest near the opening of tunnel described above. Calculate the speed of particle as it passes through the center of the sphere.
View SolutionThere are three conecentric hollow spheres of radii a, b and c and they are charged with charges `q_(1),q_(2)` and `q_(3)` respectively. Calculate the potential of the spheres.
View SolutionWhat will be the potential at the middle spherical shell in the previous example?
View SolutionOne plate of a parallel plate capacitor is given a charge of `2muC`. What charge will appear on four surfaces of the capacitor?
View Solution27 spherical drops, each carrying a charge of `10^(-3)muC` that are at potential of 1,000 volts are combined to form a bigger drop. What would be the potential of this bigger drop?
View SolutionA potential difference of 20 volts develops between the plates of the capacitor when `2xx10^(12)` electrons are transferred from one plate of the capacitor to the other. What should be the capacitance of capacitor?
View SolutionA capacitor of capacitance C is found to store a charge 480 `muC` when it is connected across a battery of potential difference V. Charge stored in the capacitor becomes `160muC` when potential difference is reduced by 160V. Calculate C and V.
View SolutionTwo parallel plate capacitors are found to store the same amount of charge when connected to the same battery one by one. Their plate areas are 300 `cm^(2)` and `700cm^(2)`. Separation between the plates of first capacitor is 2 mm. Calculate separation between the plates of second capacitor.
View SolutionA capacitor stores a charge of amount 0.05 C when connected across a battery of 100 V for a sufficient time. How much energy will be relaeased by this capacitor when it is discharged?
View SolutionA parallel plate capacitor of capacitance 2 `muF` is fully charged to a potential difference of 500 volts and then disconnected from the battery. Using insulating handles, separation between the paltes is made thrice the initial value. What will be the new potential difference between the plates of the capacitor and by what amount stored energy changes in this process?
View SolutionSomeone suggested using a 5,000 `muF` capacitor to generate flash for a camera. A capacitor is to charged slowly and completely up to a potential difference of 10V. At the time of generating flash, all stored energy of a capacitor is discharged through a discharge tube in such a manner that flash only time 100 `mus` to release the total energy of the capacitor. Calculate the power of camera flash.
View SolutionA parallel plate capacitor of capacitance 40 `muF` is charged to a potential difference of 250 V and then the battery is disconnected. Separation between the paltes of the capacitor is 5 mm. A dielectric slab of dielectric constant 5 and thickness 3 mm is introduced in -between the plates of capacitor. Calcualte final charge and potential difference between the plates. Also calculate energy loss due to the introduction of dielectric slab.
View SolutionFind the total work done by the battery in the given circuit.
View SolutionTwo capacitors when connected in parallel are equivalent to `6muF` and when the same are connected in series then the equivalent becomes 1.5 `muF`. Calculate the individual capacitances.
View SolutionWhen n, identical capacitors are connected in series then equivalent capacitance becomes x, and when the same are connected in parallel then equivalent capacitance becomes y. Calculate y/x.
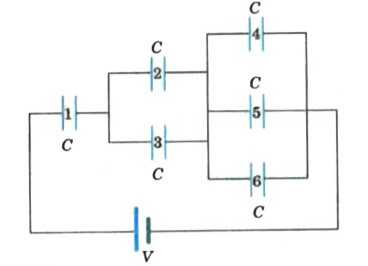
View SolutionRefer to the schematic circuit diagram and calculate the total amount of charge supplied by the battery.
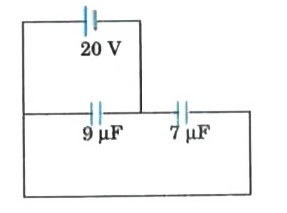
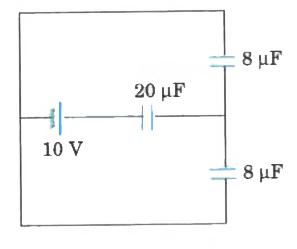
View SolutionFind the charges stored in each of the capacitors shown in the circuit diagram.
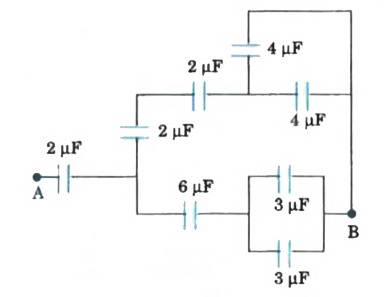
View SolutionCalculate equivalent capacitance between points A and B in the circuit shown. What charge will be supplied by the battery of 20V when connected between the points A and B?
View SolutionA capacitor of capacitance 5 `muF` is charged to a potential difference of 10 volts and another capacitor of capacitance 9 `muF` is charged to a potential difference of 8 volts. Now these two capacitors are connected in such a manner that the positive plate of one is connected to the positive plate of other. Calculate the common potential difference across the two capacitors.
View SolutionFind the equivalent capacitance between A and B for the following network of capacitors.

View Solution
SOLVED EXAMPLES questions and complete solutions for chapter ELECTROSTATIC POTENTIAL AND CAPACITANCE of MODERN PUBLISHERS PHYSICS (HINGLISH) of Class 12
All Exercises from MODERN PUBLICATION Class 12 PHYSICS ELECTROSTATIC POTENTIAL AND CAPACITANCE
- Chapter Practice Test
- Competition file (ASSERTION REASON TYPE QUESTIONS)
- Competition file (INTEGER TYPE QUESTIONS)
- Competition file (MATCHING TYPE QUESTIONS)
- Competition file (MATRIX TYPE QUESTIONS)
- Competition file (MULTIPLE CHOICE QUESTIONS based on a given passage/comprehension)
- Competition file (NCERT Exemplar Problems: Multiple Choice Questions Type-I)
- Competition file (NCERT Exemplar Problems: Multiple Choice Questions Type-II)
- Conceptual Questions
- Higher Order Thinking Skills & Advanced Level (QUESTIONS WITH ANSWERS)
- NCERT FILE Solved (Additional Exercises)
- NCERT FILE Solved (Additional Exercises) (Answer carefully)
- NCERT FILE Solved (Additional Exercises) (Answer the following)
- NCERT FILE Solved (Exemplar Problems) (Short Answer Type Questions)
- NCERT FILE Solved (Exemplar Problems) (Very Short Answer Type Questions)
- NCERT FILE Solved (Textbook Exercise)
- PRACTICE PROBLEMS 1
- PRACTICE PROBLEMS 2
- PRACTICE PROBLEMS 3
- PRACTICE PROBLEMS 4
- PRACTICE PROBLEMS 5
- Revision Exercises (Additional Questions)
- Revision Exercises (Fill in the Blanks)
- Revision Exercises (Long Answer Questions)
- Revision Exercises (Numerical Problems)
- Revision Exercises (Short Answer Questions)
- Revision Exercises (Very Short Answer Questions)
- SOLVED EXAMPLES
- Tough & Tricky PROBLEMS