Complete Solutions to LEVEL-V of chapter ATOMIC PHYSICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ATOMIC PHYSICS |
| NARAYANA | LEVEL-V |
| Number Of Questions | 51 |
| Academic Year | 2023-24 |
If a hydrogen atom at rest, emits a photon of wavelength `lambda`, the recoil speed of the atom of mass m is given by :
View SolutionA positronium "atom" is a system that consists of a positron and an electron that orbit each other. Campare the wavelengths of the spectral lines of positronium with those of ordinary hydrogen.
View SolutionThe intensity of X- ray from a coolidge tube is plotted againest wavelength `lambda` as shown in the figure . The minimum wavelength found `lambda_(c)` and the wavelength of the` k_(a)` line is `lambda_(lambda)`, As the accelerating voliage is increase
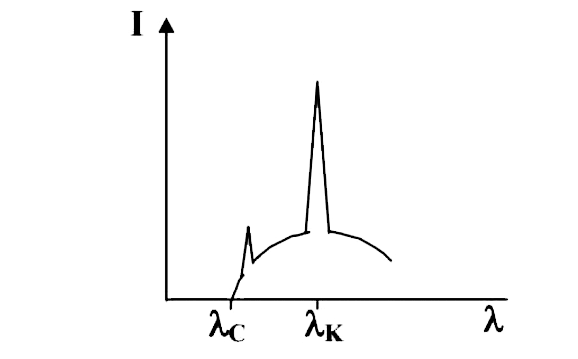
View SolutionThe potential difference applying to an X- ray tube is `5kV` and the current through it is `3.2mA`. Then the number of electrons striking the target per second is
View SolutionA hydrogen atom and a `Li^(2+)` ion are both in the second excited state. If `l_H` and `l_(Li)` are their respective electronic angular momenta, and `E_H and E_(Li)` their respective energies, then
(a) `l_H gt l_(Li) and |E_H| gt |E_(Li)|`
(b) `l_H = l_(Li) and |E_H| lt |E_(Li)|`
(C ) `l_H = l_(Li) and |E_H| gt |E_(Li)|`
(d) `l_H lt l_(Li) and |E_H| lt|E_(Li)|`
View SolutionIf the atom`(_100)Fm^(257)` follows the Bohr model the radius of `_(100)Fm^(257)` is `n` time the Bohr radius , then find `n` .
View SolutionThe electric potential between a proton and as electron is given by `V= V_(0) ln (r )/(r_(0))` , where`r_(0)` is a constant . Assuming Bohr's model to be applicable , write variation of `r_(n)` with `n,n` being the principal quantum number ?
View SolutionThe wave length of `Kbeta` X-ray of certain metal is `12.42`pm . It takes `10Kev` to remove the electron from M shell of an atom of that metal the minimum accelerating voltage that should be applied across the X-ray tube , so that a `K_(a)` X-ray would be produced is (`hc=1242eVnm`)
View SolutionA photon collides with a stationary hydrogen atom in ground state inelastically. Energy of the colliding photon is 10.2 eV. After a time interval of the order of micro second another photon collides with same hydrogen atom inelastically with an energy of 15eV. What wil be observed by the detector?
(a) 2 photons of energy 10.2 eV
(b) 2 photons of energy 1.4 eV
(c ) One photon of energy 10.2 eV and an electron of energy 1.4 eV
(d) One photon of energy 10.2 eV and another photon of energy 1.4 eV
View SolutionThe potential energy of a particle of mass `m` is given by
`V(x) = E_0` when `x= lex le 1 `and `xgt 1` repectively.
`lambda_(1) and lambda_(2) ` are the de - Broglie wavelength of the particle, ,if the total energy of particle is `2 E_(0)` find `lambda_(1) // lambda_(2)`
View SolutionThe largest wavelength in the ultraviolet region of the hydrogen spectrum is `122` nm. The smallest wavelength in the infrared region of the hydrogen spectrum (to the nearest integer) is
View SolutionElectrons with de- Broglie wavelength `lambda` fall on the target in an X- rays tube . The cut off wavelength of the emitted X- rays is
View SolutionWhich one of the following statement is `WRONG` in the context of X- rays generated from X- rays tube ?
View SolutionThe potential different across the Coolidge tube is `20 kV and 10 m A` current flows through the voltage supply. Only `0.5%` of the energy carried by the electrons striking the largest is converted into X-ray. The power carried by the X-ray beam is `p`. Then
View SolutionIn a photoelectric experiment anode potential is ploted against plate current.
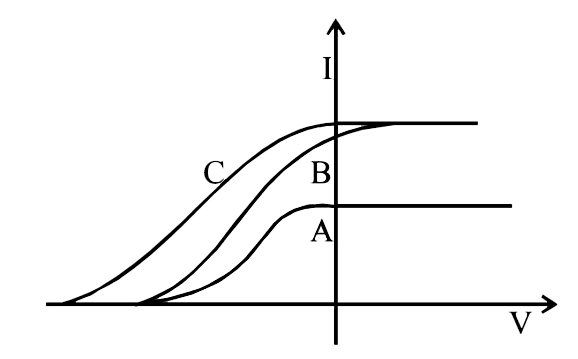
View SolutionLet `A_(0)` be the area enclined by the orbit in a hydrogen atom .The graph of in `(A_(0) //A_(1))` against `ln(n)`
View SolutionThe potential difference applied to an X-ray tube is increased. As a result, in the emitted radiation,
View SolutionWhen a hydrogen atom is excited from ground state to first excited state, then
View SolutionTwo electrons starting from rest are accelerated by equal potential difference.
View SolutionWhen an electron moving at a high speed strikes a metal surface, which of the following are possible?
(i) The entire energy of the electron may be converted into an X-ray photon
(ii) Any fraction of energy of the electron may be converted into an X-ray photon
(iii) The entire energy of the electron may get converted to heat
(iv) The electron may undergo elastic collision with the metal surface
View Solutionconsider a hypothetical atom with single electron . In this atom, when an electron de-excites from energy level `n=xx` to `n=2,` wavelength (lambda) of the radiation emitted is given by lambda =`(Ax^(2))/(x^(2)-4)`(where`A` is a eonstant). Choose the correct alternatives.
View SolutionIf, in a hydrogen atom, radius of nth Bohr orbit is `r_(n)` frequency of revolution of electron in nth orbit is `f_(n)` and area enclosed by the nth orbit is `A_(n)` , then which of the pollowing graphs are correct?
View SolutionThe electron in a hydrogen atom makes a transition `n_(1) rarr n_(2)`, where `n_(1)` and `n_(2)` are the principle quantum numbers of the two states. Assume the Bohr model to be valid. The time period of the electron in the initial state is eight times that in the final state. the possible values of `n_(1)` and `n_(2)` are
View SolutionIn a mixture of `H- He^(+)` gas (`He+ `is singly ionized He atom), `H` atom and `He+` ions are excited to their respective first excited state. Subsequently `H` atoms transfer their total excitation energy to `He+` ions (by collisions) Assume that the bohr model of atom is exactly valid.
The quantum number `n` of the state finally populated in `He^(+)` inos is -
View SolutionIn a mixture of `H- He^(+)` gas (`He+ `is singly ionized He atom), `H` atom and `He+` ions are excited to their respective first excited state. Subsequently `H` atoms transfer their total excitation energy to `He+` ions (by collisions) Assume that the bohr model of atom is exactly valid.
The wavelength of light emitted in the visible region by `He+` lons after collisions with `H` atoms is -
View SolutionIn a mixture of `H- He^(+)` gas (`He+ `is singly ionized He atom), `H` atom and `He+` ions are excited to their respective first excited state. Subsequently `H` atoms transfer their total excitation energy to `He+` ions (by collisions) Assume that the bohr model of atom is exactly valid.
The ratio of the kinetic energy of the `n = 2` electron for the `H` atom to the of `He^(+)` lon is -
View SolutionThe key feature of Bohr's spectrum of hydrogen atom is the quantization of angular momentum when an electron is revolving around a proton. We will extend this to a general rotational motion to find quantized rotational energy of a diatomic molecule assuming it to be rigid.The rule to be applied is Bohr's quantization condition.
A diatomic molecule has moment of inertia `I`. By Bohr's quantization condition its rotational energy in the `n^(th)` level (`n = 0` is not allowed ) is
View SolutionThe key feature of Bohr's spectrum of hydrogen atom is the quantization of angular momentum when an electron is revolving around a proton. We will extend this to a general rotational motion to find quantized rotational energy of a diatomic molecule assuming it to be rigid.The rule to be applied is Bohr's quantization condition.
it is found that the excitation from ground to the first excited state of rotation for the `CO` molecule is close to `(4)/(pi) xx 10^(11) Hz` then the moment of inertia of `CO` molecule about its center of mass is close to
`(Take h = 2 pi xx 10^(-34) J s )`
View SolutionThe key feature of Bohr's spectrum of hydrogen atom is the quantization of angular momentum when an electron is revolving around a proton. We will extend this to a general rotational motion to find quantized rotational energy of a diatomic molecule assuming it to be rigid.The rule to be applied is Bohr's quantization condition.
In a `CO` molecule, the distance between `C (mass = 12 a. m. u ) and O (mass = 16 a.m.u)` where `1 a.m.u = (5)/(3) xx 10^(-27) kg , `is close to
View SolutionWhen a particle is restricted to move along x-axis between `x=0` and `x=a`, where `alpha` if of nenometer dimension, its energy can take only certain specific values. The allowed energies of the particle moving in such a restricted region, correspond to the formation of standing waves with nodes at its ends `x=0` and `x=a`. The wavelength of this standing wave is related to the linear momentum p of the particle according to the de Broglie relation. The energy of the particle of mass m is related to its linear momentum as `E=(p^2)/(2m)`. Thus the energy of the particle can be denoted by a quantum number `n` taking values 1,2,3, ...(`n=1`, called the ground state) corresponding to the number of loops in the standing wave.
Use the model described above to answer the following three questions for a particle moving along the line from `x=0` to `x=alpha`. Take `h=6.6xx10^(-34)Js` and `e=1.6xx10^(-19)` C.
Q. The allowed energy for the particle for a particular value of n is proportional to
View SolutionWhen a particle is restricted to move along x-axis between `x=0` and `x=a`, where `alpha` if of nenometer dimension, its energy can take only certain specific values. The allowed energies of the particle moving in such a restricted region, correspond to the formation of standing waves with nodes at its ends `x=0` and `x=a`. The wavelength of this standing wave is related to the linear momentum p of the particle according to the de Broglie relation. The energy of the particle of mass m is related to its linear momentum as `E=(p^2)/(2m)`. Thus the energy of the particle can be denoted by a quantum number `n` taking values 1,2,3, ...(`n=1`, called the ground state) corresponding to the number of loops in the standing wave.
Use the model described above to answer the following three questions for a particle moving along the line from `x=0` to `x=alpha`. Take `h=6.6xx10^(-34)Js` and `e=1.6xx10^(-19)` C.
Q. If the mass of the particle is `m=1.0xx10^(-30)`kg and `alpha=6.6nm`, the energy of the particle in its ground state is closest to
View SolutionWhen a particle is restricted to move along x-axis between `x=0` and `x=a`, where `alpha` if of nenometer dimension, its energy can take only certain specific values. The allowed energies of the particle moving in such a restricted region, correspond to the formation of standing waves with nodes at its ends `x=0` and `x=a`. The wavelength of this standing wave is related to the linear momentum p of the particle according to the de Broglie relation. The energy of the particle of mass m is related to its linear momentum as `E=(p^2)/(2m)`. Thus the energy of the particle can be denoted by a quantum number `n` taking values 1,2,3, ...(`n=1`, called the ground state) corresponding to the number of loops in the standing wave.
Use the model described above to answer the following three questions for a particle moving along the line from `x=0` to `x=alpha`. Take `h=6.6xx10^(-34)Js` and `e=1.6xx10^(-19)`C
Q. The speed of the particle that can take discrete values is proportional to
View SolutionSTATEMENT - 1
If the accelerating potential in an X - rays tube is increased, the wavelength of the characteristic X- rays do not change .
STATEMENT -2
When an electron beam strikes the target in an X- rays tube, part of the kinectic energy is converted into X - rays energy .
View SolutionThis question has statement - 1 and statement - 2 of the four choice given after the statements choose the one that best describes the two statements
statement - 1 : A metallic surface is irradiated by a monochromatic light of frequency ` v gt v_(0)` (the threshold frequency). The maximum kinetic energy and the stopping potential are `K_(max) and V_(0)` respectively if the frequency incident on the surface is doubled , both the `K_(max) and V_(0)` are also doubled
statement - 2 : The maximum kinetic energy and the stopping potential of photoelectron emitted from a surface are linearly dependent on the frequency of incident light
View SolutionA hydrogen atom emits a photon corresponding to an electron transition from `n = 5` to `n = 1`. The recoil speed of hydrogen atom is almost (mass of proton `~~1.6 xx 10^(-27) kg)`.
View Solution`K_alpha` wavelength emitted by an atom of atomic number Z=11 is `lambda`. Find the atomic number for an atom that emits `K_alpha` radiation with wavelength `4lambda`.
(a) Z=6 (b) Z=4
(c ) Z=11 (d) Z=44.
View SolutionAn electron in nth excited state in a hydrogen atom comes down to first excited state by emitting ten different wavelength. Find value of `n` (an integer).
View SolutionThe ratio between total acceleration of the electron in singly ionized helium atom and hydrogen atom (both in ground state) is
View SolutionThe shortest wavelength of the Brackett series of a hydrogen-like atom (atomic number of `Z` ) is the same as the shortest wavelength of the Balmer series of hydrogen atom. The value of `z` is
View SolutionA hydrogen like atom (atomic number `Z`) is in a higher excited state of quantum number `6`. The excited atom can make a transition to the first excited state by successively emitting two photons of energies `10.2eV` and `17.0eV` respectively . Determine the value of `X` . (ionization energy of H-atom is `13.6eV`.)
View SolutionThe electric potential between a proton and as electron is given by `V= V_(0) ln (r )/(r_(0))` , where`r_(0)` is a constant . Assuming Bohr's model to be applicable , write variation of `r_(n)` with `n,n` being the principal quantum number ?
View SolutionIn a hypothetical system , a partical of mass `m` and charge `-3 q` is moving around a very heavy partical chaRGE `q`. Assume that Bohr's model is applicable to this system , then velocuity of mass `m` in the first orbit is
View Solution`29` electron are remove from `Zn` atom `(Z=30)` by certain means . The minimum energy needed to remove the `30th` electron , will be :
View SolutionAny radiation in the ultra violet region of Hydrogen from a metal . Then the metal is, nearly
View SolutionA hydrogen atom emits a photon corresponding to an electron transition from `n = 5` to `n = 1`. The recoil speed of hydrogen atom is almost (mass of proton `~~1.6 xx 10^(-27) kg)`.
View SolutionIn a Bohr atom the electron is replaced by a particle of mass `150` times the mass of the electron and the same charge. If `a_(0)` is the radius of the first Bohr's orbit of the orbital atom, then that of the new will be .
View SolutionA hydrogen like atom (atomic number Z) is in a higher excited state of quantum number 'n' this excited atom can make a transition to the first excited state by emitting a photon of first `27.2eV`. Alternatively the atom from the same excited state can make a transition of energy `10.20eV` the value of `n` and `z` are given (ionization energy of hydrogen atom is 13.6eV)
View SolutionThe electric potential between a proton and as electron is given by `V= V_(0) ln (r )/(r_(0))` , where`r_(0)` is a constant . Assuming Bohr's model to be applicable , write variation of `r_(n)` with `n,n` being the principal quantum number ?
View SolutionThe recoil speed of a hydrogen atom after it emits a photon is going form n=5 state to n =1 state is ….. m/s.
View SolutionThe binding energy of the electron in the ground state of `He` atom is equal to `E_(0)=24.6 eV`. Find the energy required to remove both the electrons from the atom.
View SolutionAn electron in the ground state of hydrogen atom is revolving in anticlock-wise direction in a circular orbit of radius `R`.
(i) Obtain an experssion for the orbital magnetic dipole moment of the electron.
(ii) The atom is placed in a uniform magnetic induction `vec(B)` such that the plane - normal of the electron - orbit makes an angle of ` 30^(@)` with the magnetic induction . Find the torque experienced by the orbiting electron.
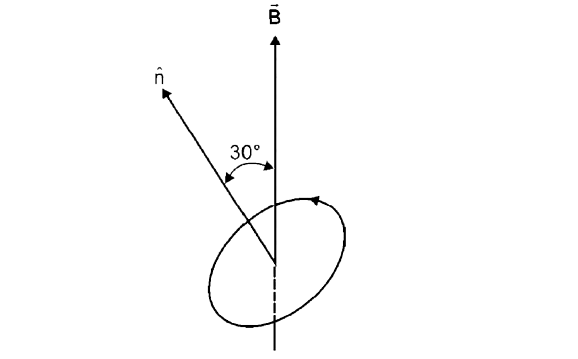
View Solution
LEVEL-V questions and complete solutions for chapter ATOMIC PHYSICS of NARAYANA PHYSICS (HINGLISH) of Class 12