Complete Solutions to Passage of chapter EXPERIMENTAL PHYSICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | EXPERIMENTAL PHYSICS |
| NARAYANA | Passage |
| Number Of Questions | 6 |
| Academic Year | 2023-24 |
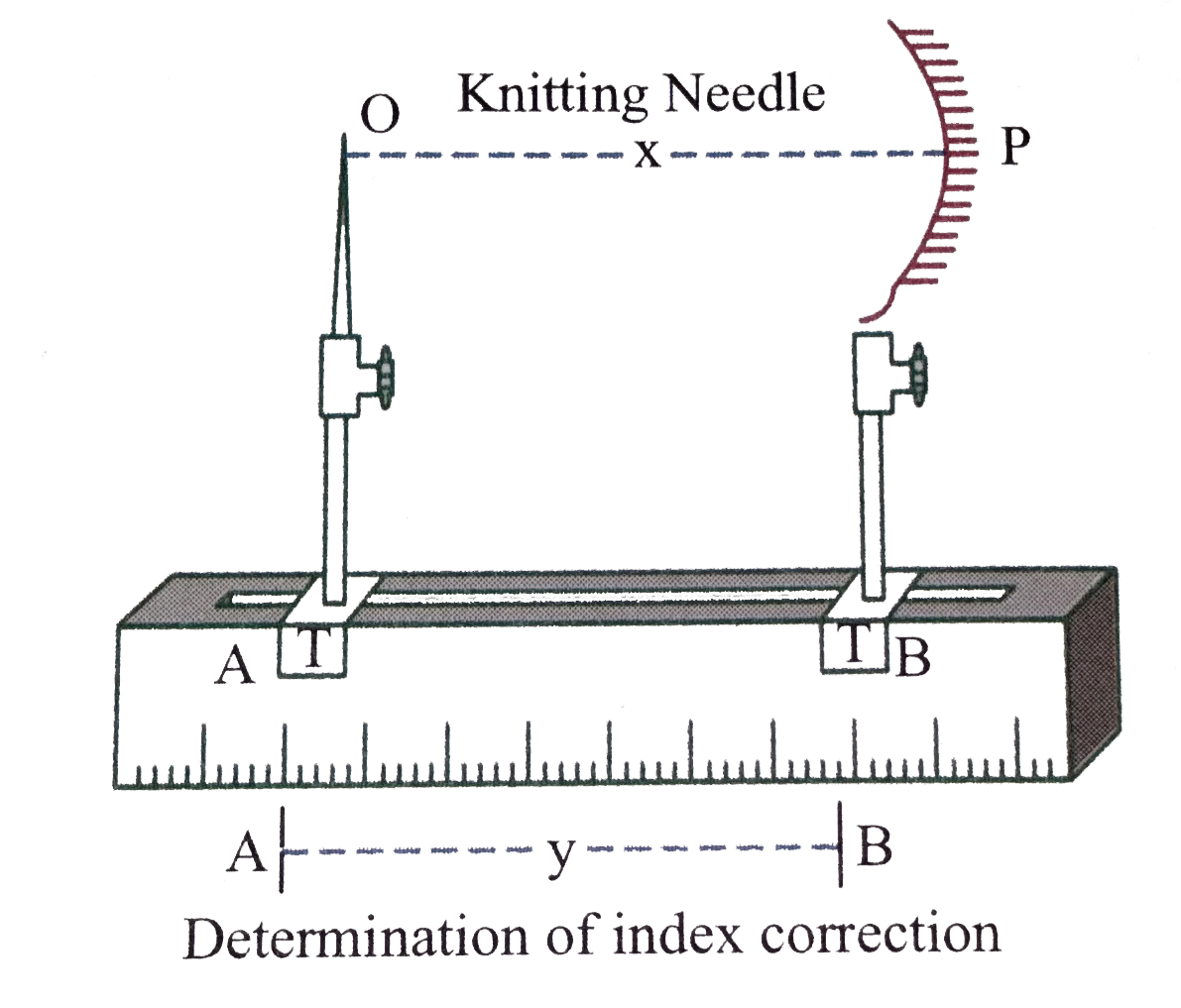
In `u-v` method, we require the distance between object or image from the pole (vertex) of the mirror (actual distance). But practically we measure the distance between the indices `A` and `B`. (Observed distance). Which need not exactly co-inside with object and pole, there can be a slight mismatch called index error, which will be constant for every observation.

Index error=Observed distance-Actual distance(Just like zero error in screw guage, it is the excess reading).
To determine index error, mirror and object needle and placed at arbitary position. For measuring actual distance, a knitting needle is just fitted between the pole of mirror and object needle `O`. The length of knitting needle will give the actual object distance while the seperation between indices `A` and `B` at that instant is the observed distance.
So index error is-
`e=`Observed distance-Actual distance
`=` Separation between indices `A` and `B`- Length of knitting neddle once we get `e`, in
every observation, we get
Actual distance=Observed distance (separation between the indices)- Excess reading(e) There is an another term, Index corraction which is invert of index error.
Index correction=-index error
To find index error for `u`, when a knitting needle of length `20.0cm` is adjusted between pole and object needle, the sepertion between the indices of object needle and mirror was observed to be `20.2cm`. Index corraction for u is
View SolutionIn `u-v` method, we require the distance between object or image from the pole (vertex) of the mirror (actual distance). But practically we measure the distance between the indices `A` and `B`. (Observed distance). Which need not exactly co-inside with object and pole, there can be a slight mismatch called index error, which will be constant for every observation.
Index error=Observed distance-Actual distance(Just like zero error in screw guage, it is the excess reading).
To determine index error, mirror and object needle and placed at arbitary position. For measuring actual distance, a knitting needle is just fitted between the pole of mirror and object needle `O`. The length of knitting needle will give the actual object distance while the seperation between indices `A` and `B` at that instant is the observed distance.
So index error is-
`e=`Observed distance-Actual distance
`=` Separation between indices `A` and `B`- Length of knitting neddle once we get `e`, in
every observation, we get
Actual distance=Observed distance (separation between the indices)- Excess reading(e) There is an another term, Index corraction which is invert of index error.
Index correction=-index error
To find index error for `v`, when the same knitting needle is adjusted between the pole and the image needle, the separation between the indices of image needle and mirror was found to be `19.9cm`. Index error for `v` is
View SolutionIn `u-v` method, we require the distance between object or image from the pole (vertex) of the mirror (actual distance). But practically we measure the distance between the indices `A` and `B`. (Observed distance). Which need not exactly co-inside with object and pole, there can be a slight mismatch called index error, which will be constant for every observation.
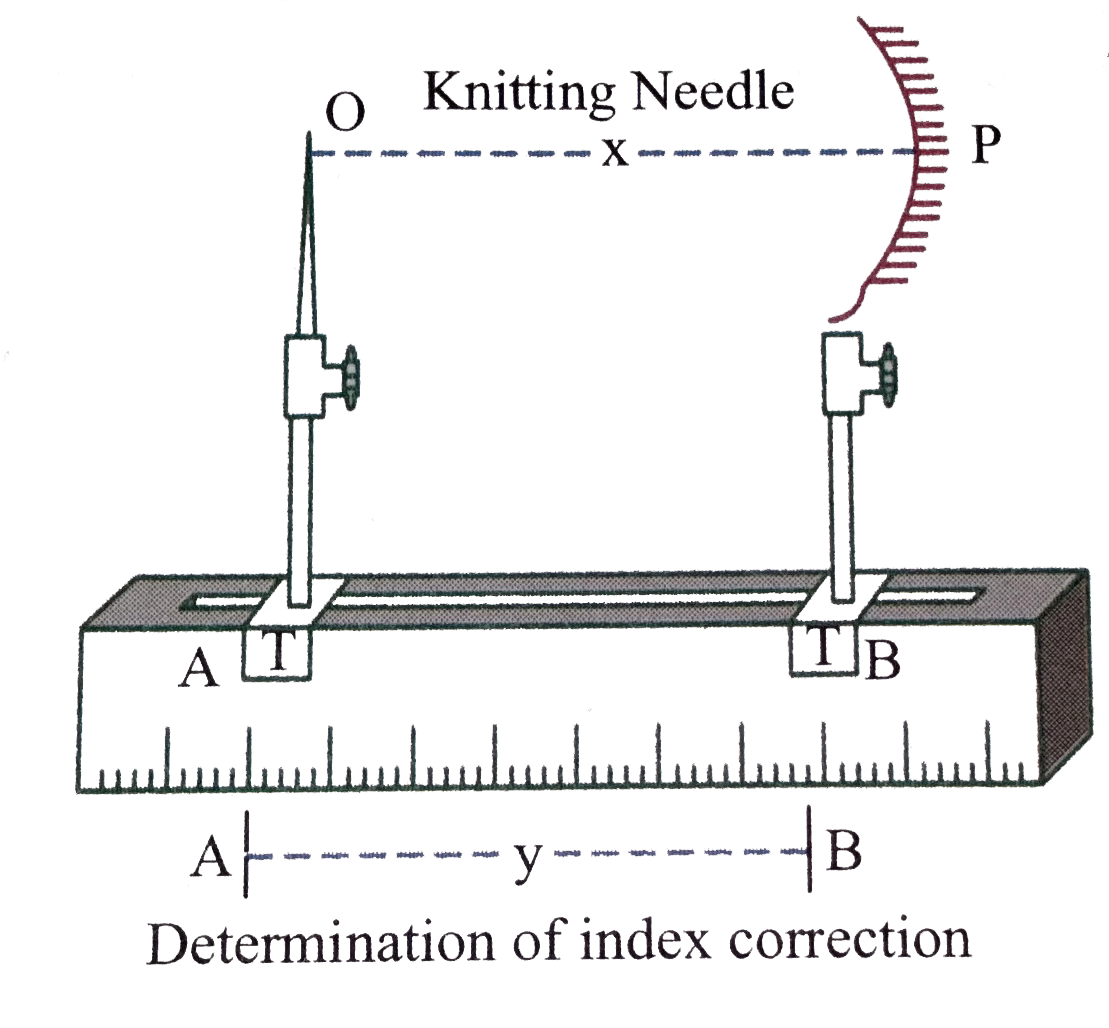
Index error=Observed distance-Actual distance(Just like zero error in screw guage, it is the excess reading).
To determine index error, mirror and object needle and placed at arbitary position. For measuring actual distance, a knitting needle is just fitted between the pole of mirror and object needle `O`. The length of knitting needle will give the actual object distance while the seperation between indices `A` and `B` at that instant is the observed distance.
So index error is-
`e=`Observed distance-Actual distance
`=` Separation between indices `A` and `B`- Length of knitting neddle once we get `e`, in
every observation, we get
Actual distance=Observed distance (separation between the indices)- Excess reading(e) There is an another term, Index corraction which is invert of index error.
Index correction=-index error
In some observation, the observed object distance (Separation between indices of object needle and mirror) is `30.2cm`, and the observed image distance is `19.9cm`. Using index correction from previous two equations, estimate the focal distance of the concave mirror!
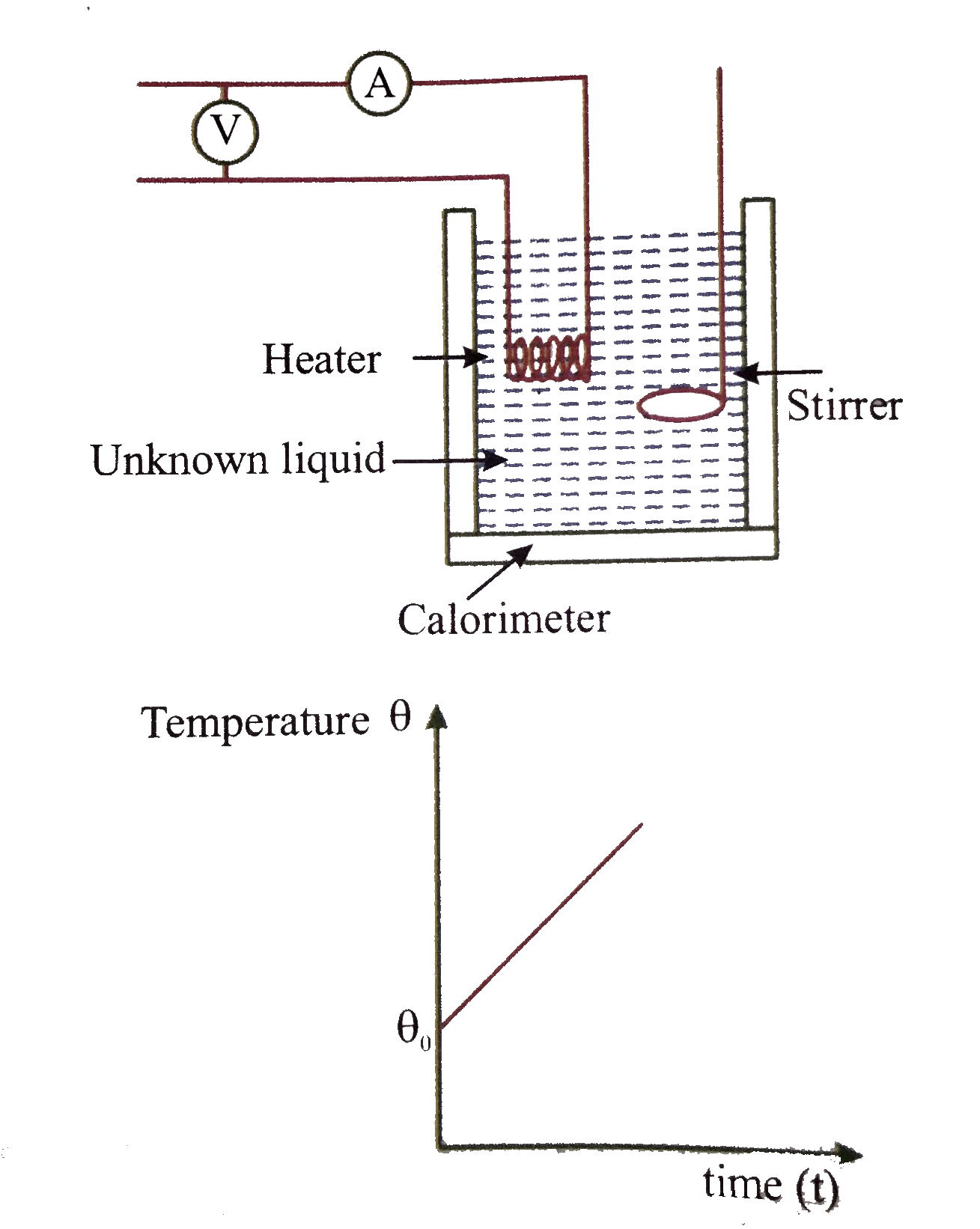
View SolutionFigure shows an electrical calorimeter to determine specific heat capacity of an unknown liquid, First of all, the mass of empty calorimeter (a copper container) is measured and suppose it is `m_(1)`. Then the unknown liquid is poured in it. Now the combined mass of calorimeter+liquid system is measured and let it be `m_(2)`. So the mass of liquid is `(m_(2)-m_(1))`. Initially both were at room temperature (`theta_(0)`).
Now a heater is immeresed in if for time interval `t`. The voltage drop across the heater is `V` and current passing through it is `I`. Due to heat supplied, the temperature of both the liquid and calorimeter will rise simultaneously. After `t sec`, heater was switched off, and final temperature is `theta_(r)`. If there is no heat loss to surroundings. Heat supplied by the heater=Heat absorbed by the liquid+heat absorbed by the calorimeter `(VI)t=(m_(2)-m_(1))S_(1)(theta_(f)-theta_(0))+m_(1)S_(c)(theta_(f)-theta_(0))`
The specific heat of the liquid `S_(1)=(((VI)t)/(theta_(f)-theta_(0))-m_(1)S_(c))/((m_(2)-m_(1)))`
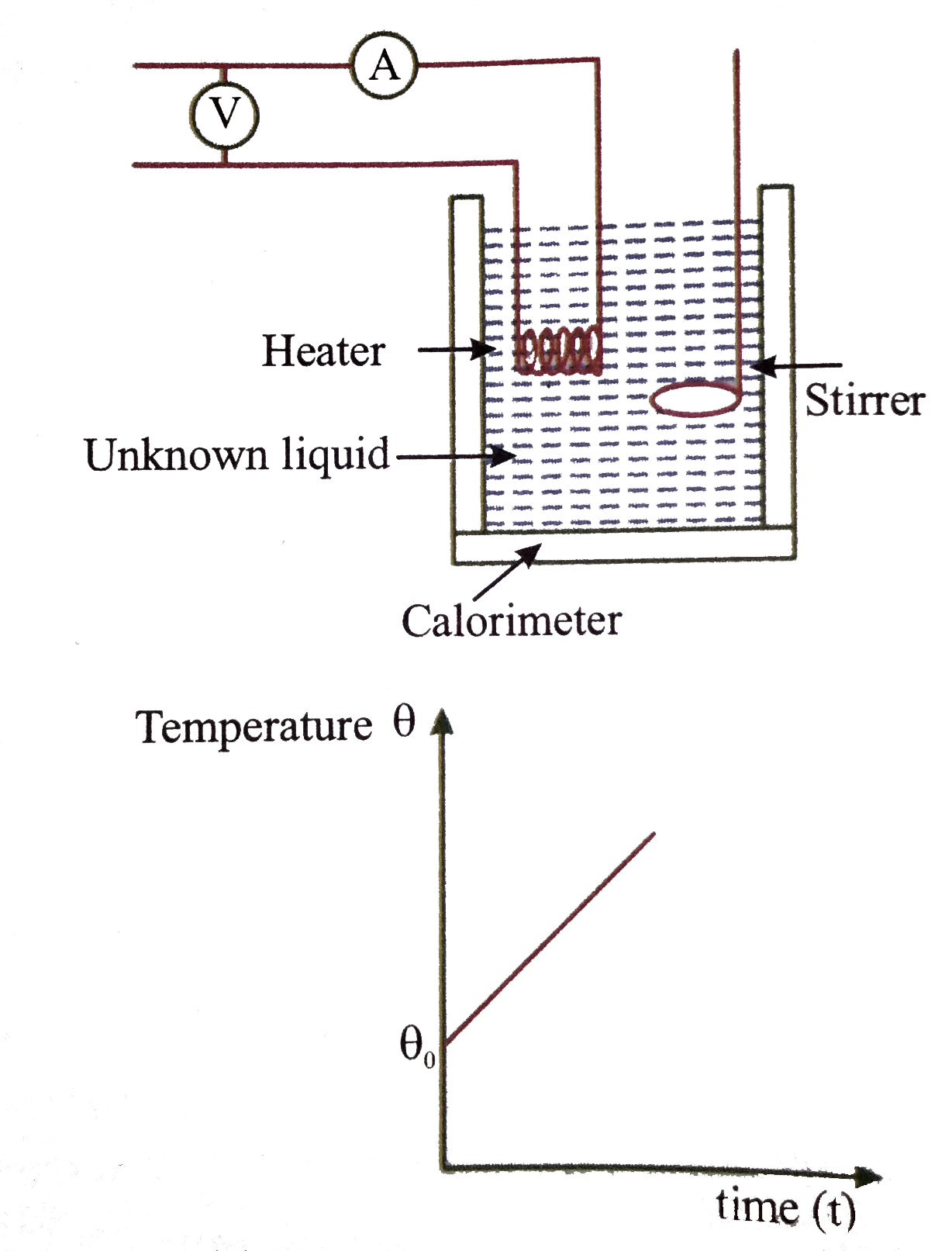
Radiation correction: There can be heat loss to environment. To compensate this loss, a correction is introduced.
Let the heater was on for `t sec`, and then it is switched off. Now the temperature of the mixture falls due to heat loss to environment. The temperature of the mixture is measured `t//2 sec`. after switching off. Let the fall in temperature during this time is `varepsilon`
Now the corrected final temperature is taken as `theta_(f)=theta_(f)+varepsilon`
In this experiment voltage across the heater is `100.0V` and current is `10.0A`, and heater was switched on for `t=700.0 sec`. Initially all elements were at room temperature `theta_(@)=10.0^(@)C` and final temperature was measured as `theta_(f)=73.0^(@)C`.
Mass of empty calorimeter ws `1.0 kg` and the combined mass of calorimeter + liquid is `3.0 kg`. The specific heat capacity of the calorimeter `=3.0xx10^(3)J//kg^(@)C`. The falls in temperature `350` second after switching off the heater was `7.0^(@)C`. Find the specific heat capacity of the unknown liquid in proper significant figures.
View SolutionFigure shows an electrical calorimeter to determine specific heat capacity of an unknown liquid, First of all, the mass of empty calorimeter (a copper container) is measured and suppose it is `m_(1)`. Then the unknown liquid is poured in it. Now the combined mass of calorimeter+liquid system is measured and let it be `m_(2)`. So the mass of liquid is `(m_(2)-m_(1))`. Initially both were at room temperature (`theta_(0)`).
Now a heater is immeresed in if for time interval `t`. The voltage drop across the heater is `V` and current passing through it is `I`. Due to heat supplied, the temperature of both the liquid and calorimeter will rise simultaneously. After `t sec`, heater was switched off, and final temperature is `theta_(r)`. If there is no heat loss to surroundings. Heat supplied by the heater=Heat absorbed by the liquid+heat absorbed by the calorimeter `(VI)t=(m_(2)-m_(1))S_(1)(theta_(f)-theta_(0))+m_(1)S_(c)(theta_(f)-theta_(0))`
The specific heat of the liquid `S_(1)=(((VI)t)/(theta_(f)-theta_(0))-m_(1)S_(c))/((m_(2)-m_(1)))`
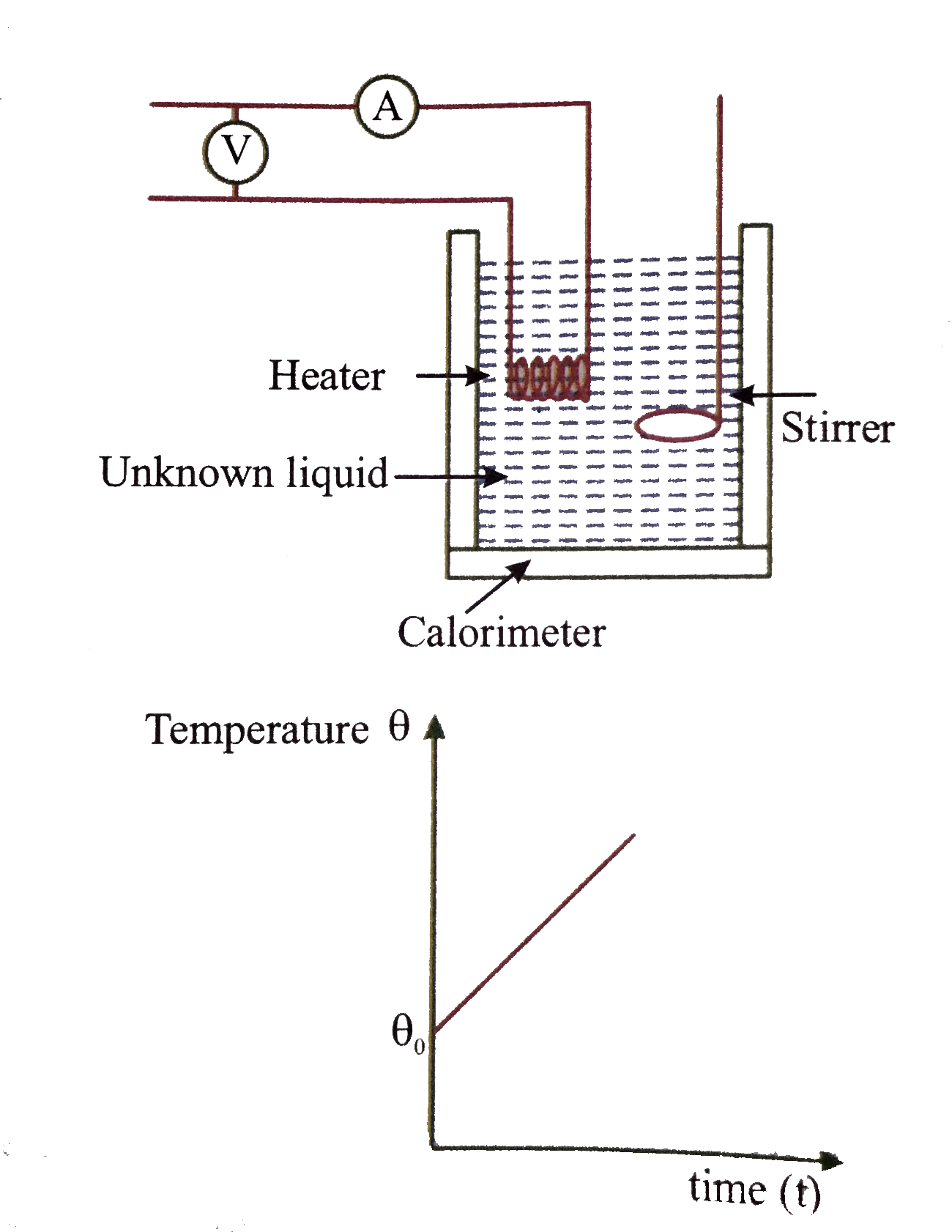
Radiation correction: There can be heat loss to environment. To compensate this loss, a correction is introduced.
Let the heater was on for `t sec`, and then it is switched off. Now the temperature of the mixture falls due to heat loss to environment. The temperature of the mixture is measured `t//2 sec`. after switching off. Let the fall in temperature during this time is `varepsilon`
Now the corrected final temperature is taken as `theta_(f)=theta_(f)+varepsilon`
If mass and specific heat capacity of calorimeter is negligible, what would be maximum permissible error in `S_(l)`. Use the date mentioned below.
`m_(1)to`, `S_(l)to0`, `m_(2)=1.00kg`,
`V=10.0V`, `I=10.0A`,
`t=1.00xx10^(2)sec`, `theta_(0)=15^(@)C`,
Corrected `theta_(1)=65^(@)C`
View SolutionFigure shows an electrical calorimeter to determine specific heat capacity of an unknown liquid, First of all, the mass of empty calorimeter (a copper container) is measured and suppose it is `m_(1)`. Then the unknown liquid is poured in it. Now the combined mass of calorimeter+liquid system is measured and let it be `m_(2)`. So the mass of liquid is `(m_(2)-m_(1))`. Initially both were at room temperature (`theta_(0)`).
Now a heater is immeresed in if for time interval `t`. The voltage drop across the heater is `V` and current passing through it is `I`. Due to heat supplied, the temperature of both the liquid and calorimeter will rise simultaneously. After `t sec`, heater was switched off, and final temperature is `theta_(r)`. If there is no heat loss to surroundings. Heat supplied by the heater=Heat absorbed by the liquid+heat absorbed by the calorimeter `(VI)t=(m_(2)-m_(1))S_(1)(theta_(f)-theta_(0))+m_(1)S_(c)(theta_(f)-theta_(0))`
The specific heat of the liquid `S_(1)=(((VI)t)/(theta_(f)-theta_(0))-m_(1)S_(c))/((m_(2)-m_(1)))`
Radiation correction: There can be heat loss to environment. To compensate this loss, a correction is introduced.
Let the heater was on for `t sec`, and then it is switched off. Now the temperature of the mixture falls due to heat loss to environment. The temperature of the mixture is measured `t//2 sec`. after switching off. Let the fall in temperature during this time is `varepsilon`
Now the corrected final temperature is taken as `theta_(f)=theta_(f)+varepsilon`
If the system were losing heat according to Newton's cooling law, the temperature of the mixture would change with time according to (while heater was on)
View Solution
Passage questions and complete solutions for chapter EXPERIMENTAL PHYSICS of NARAYANA PHYSICS (HINGLISH) of Class 12