Complete Solutions to Level-V Multiple answer questions of chapter NUCLEAR PHYSICS of Class 12 book with complete answers and questions

Regarding the nuclear forces, choose the correct options.

Regarding a nucleus choose the correct options.

Choose the correct alternative

For a certain radioactive substance, it is observed that after `4h`, only `6.25%` of the original sample is left undeacyed. It follows that.

Choose the correct options

A nuclide `A` undergoes `alpha`-decay and another nuclides `B` undergoes `beta`-decay

Assume that the nuclear binding energy per uncleon `(B//A)` versus mass number `(A)` is as shwon in Fig. Use this plot to choose the correct choice `(s)` given below:

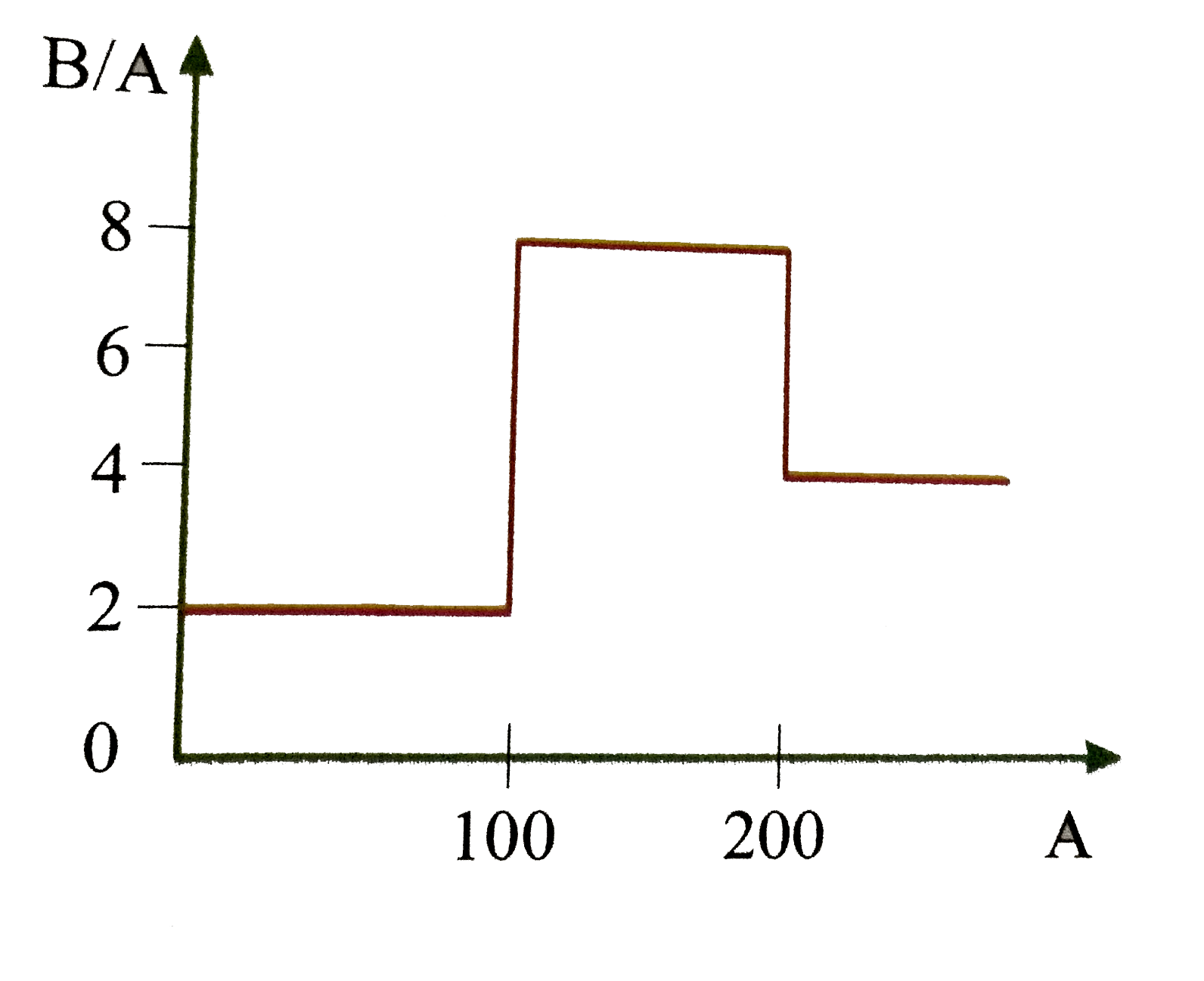
From the following equation pick out the possible nuclear fusion reactions

Many unstable nuclie can decay spontaneously to a nucleus of lower mass but differnet combination of nucleons. The process of spontaneous emission of radiation is called radioactivity substance.
Radioactive decay is a statistical process. Radiaactivity is independent of all external conditions. The number of decays per unit time or decay rate is called activity. Activity exponentially decrease with time. Mean lifetime is always greater than half-life time.
Choose the correct statemnet about radioactivity:

Many unstable nuclie can decay spontaneously to a nucleus of lower mass but differnet combination of nucleons. The process of spontaneous emission of radiation is called radioactivity substance.
Radioactive decay is a statistical process. Radiaactivity is independent of all external conditions. The number of decays per unit time or decay rate is called activity. Activity exponentially decrease with time. Mean lifetime is always greater than half-life time.
If `T_(H)` is the half-life and `T_(M)` is the mean life. Which of the following statement is correct.

Many unstable nuclie can decay spontaneously to a nucleus of lower mass but differnet combination of nucleons. The process of spontaneous emission of radiation is called radioactivity substance.
Radioactive decay is a statistical process. Radiaactivity is independent of all external conditions. The number of decays per unit time or decay rate is called activity. Activity exponentially decrease with time. Mean lifetime is always greater than half-life time.
n number of `alpha`-particels per second are being emitted by B atoms of a radioactive element. The half-life of element will be

We have two radioactive nuclei `A` and `B`. Both convert into a stable nucleus `C`. Nucleus `A` converts into `C` after emitting two two `alpha`-particles and three `beta`-particles. Nucleus `B` converts into `C` after emitting one.
`alpha`-particle anf five `beta`-particles. A time `t = 0`, nuclei of `A` are `4N_(0)` and that of `B` are `N_(0)`. Half-life of `A`(into the conversion of `C`) is `1min` and that of `B` is `2min`. Initially number of nuclei of `C` are zero.
If atomic numbers and mass numbers of `A` and `B` are `Z_(1),Z_(2),A_(1)` and `A_(2)` respectively. Then

We have two radioactive nuclei `A` and `B`. Both convert into a stable nucleus `C`. Nucleus `A` converts into `C` after emitting two two `alpha`-particles and three `beta`-particles. Nucleus `B` converts into `C` after emitting one.
`alpha`-particle anf five `beta`-particles. A time `t = 0`, nuclei of `A` are `4N_(0)` and that of `B` are `N_(0)`. Half-life of `A`(into the conversion of `C`) is `1min` and that of `B` is `2min`. Initially number of nuclei of `C` are zero.
What are number of nuclei of `C`, when number of nuclei of `A` and `B` are equal ?

We have two radioactive nuclei `A` and `B`. Both convert into a stable nucleus `C`. Nucleus `A` converts into `C` after emitting two two `alpha`-particles and three `beta`-particles. Nucleus `B` converts into `C` after emitting one.
`alpha`-particle anf five `beta`-particles. A time `t = 0`, nuclei of `A` are `4N_(0)` and that of `B` are `N_(0)`. Half-life of `A`(into the conversion of `C`) is `1min` and that of `B` is `2min`. Initially number of nuclei of `C` are zero.
At what time rate of disintergrations of `A` and `B` are equal.

The mass of nucleus `._(z)X^(A)` is less than the sum of the masses of `(A-Z)` number of neutrons and `Z` number of protons in the nucleus. The energy equivalent to the corresponding mass difference is known as the binding energy of the nucleus. A heavy nucleus of mass `M` can break into two light nuclei of mass `m_(1)` and `m_(2)` only if `(m_(1)+m_(2)) lt M`. Also two light nuclei of massws `m_(3)` and `m_(4)` can undergo complete fusion and form a heavy nucleus of mass `M` ''only if `(m_(3)+m_(4)) gt M`''. The masses of some neutral atoms are given in the table below.
`|{:(._(1)^(1)H,1.007825u,._(1)^(2)H,2.014102u,),(._(1)^(3)H,3.016050u,._(2)^(4)H,4.002603u,),(._(3)^(6)Li,6.015123u,._(3)^(7)Li,7.016004u,),(._(30)^(70)Zn,69.925325u,._(34)^(82)Se,81.916709u,),(._(64)^(152)Gd,151.91980u,._(82)^(206)Pb,205.97445u,),(._(83)^(209)Bi,208.980388u,._(84)^(210)Po,209.982876u,):}|`
The correct statement is

The mass of nucleus `._(z)X^(A)` is less than the sum of the masses of `(A-Z)` number of neutrons and `Z` number of protons in the nucleus. The energy equivalent to the corresponding mass difference is known as the binding energy of the nucleus. A heavy nucleus of mass `M` can break into two light nuclei of mass `m_(1)` and `m_(2)` only if `(m_(1)+m_(2)) lt M`. Also two light nuclei of massws `m_(3)` and `m_(4)` can undergo complete fusion and form a heavy nucleus of mass `M` ''only if `(m_(3)+m_(4)) gt M`''. The masses of some neutral atoms are given in the table below.
`|{:(._(1)^(1)H,1.007825u,._(1)^(2)H,2.014102u,),(._(1)^(3)H,3.016050u,._(2)^(4)H,4.002603u,),(._(3)^(6)Li,6.015123u,._(3)^(7)Li,7.016004u,),(._(30)^(70)Zn,69.925325u,._(34)^(82)Se,81.916709u,),(._(64)^(152)Gd,151.91980u,._(82)^(206)Pb,205.97445u,),(._(83)^(209)Bi,208.980388u,._(84)^(210)Po,209.982876u,):}|`
The kinetic energy ( in `KeV`) of the alpha particle, when the nucleus at rest undergo alpha decay, is

`4xx10^23`tritium atoms are contained in a vessel. The half-life of decay of trituim nuclei is 12.3 y. Find (a) the activity of the sample ,(b) the number of decays in the next 10 hours (c ) the number of decays in the next 6.15 y.

`4xx10^23`tritium atoms are contained in a vessel. The half-life of decay of trituim nuclei is 12.3 y. Find (a) the activity of the sample ,(b) the number of decays in the next 10 hours (c ) the number of decays in the next 6.15 y.

`4xx10^23`tritium atoms are contained in a vessel. The half-life of decay of trituim nuclei is 12.3 y. Find (a) the activity of the sample ,(b) the number of decays in the next 10 hours (c ) the number of decays in the next 6.15 y.

Consider radioactive decay of `A` to `B` with which further decays either to `X` or `Y`, `lambda_(1), lambda_(2)` and `lambda_(3)` are decay constant for `A` to `B` decay, `B` to `X` decay and Bto `Y` decay respectively. At `t=0`, the number of nuclei of `A,B,X` and `Y` are `N_(0), N_(0)` zero and zero respectively.
`N_(1),N_(2),N_(3)` and `N_(4)` are the number of nuclei of `A,B,X` and `Y` at any instant `t`.

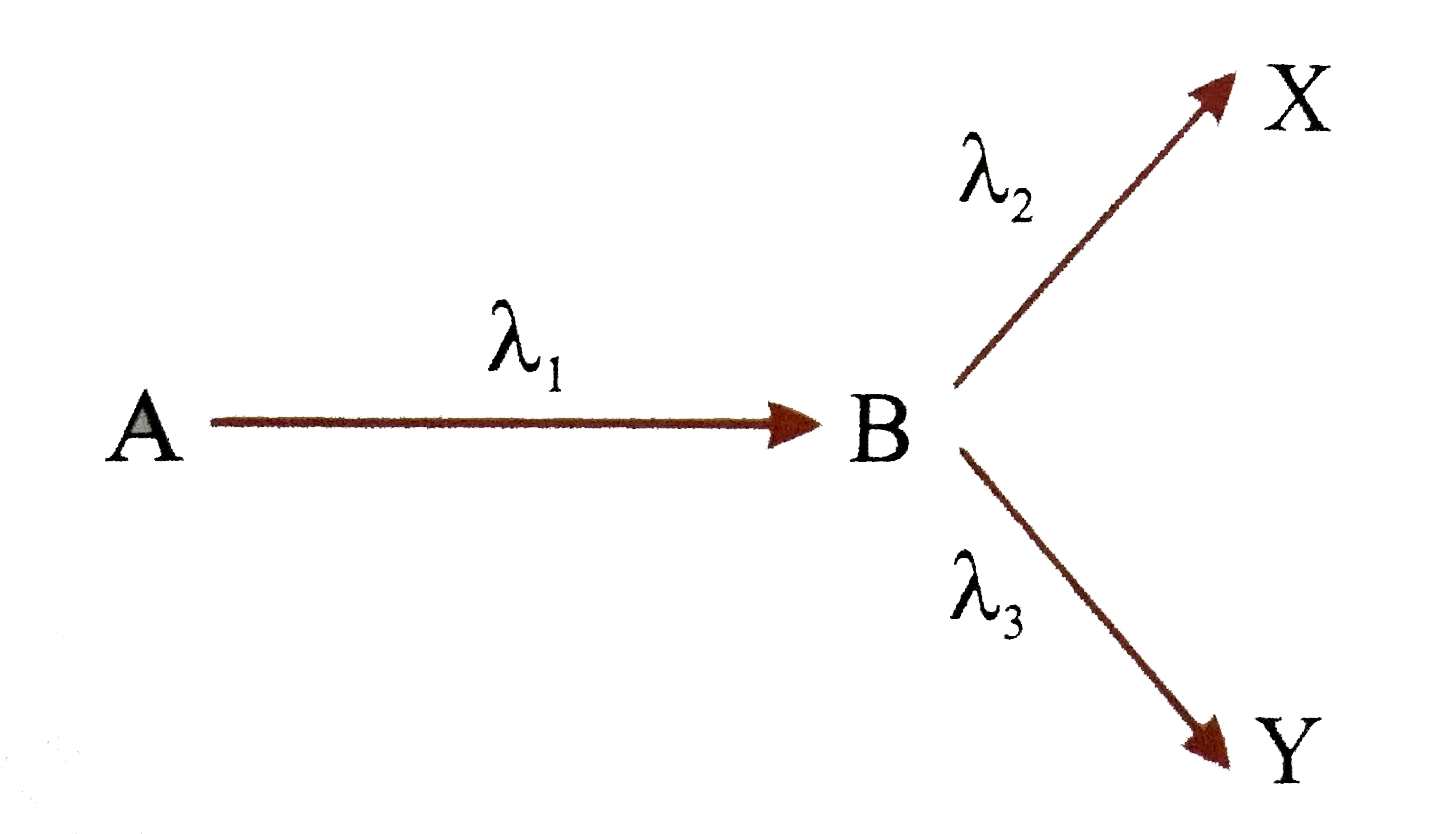
The net rate of accumulation of `B` at any instant is

Consider radioactive decay of `A` to `B` with which further decays either to `X` or `Y`, `lambda_(1), lambda_(2)` and `lambda_(3)` are decay constant for `A` to `B` decay, `B` to `X` decay and Bto `Y` decay respectively. At `t=0`, the number of nuclei of `A,B,X` and `Y` are `N_(0), N_(0)` zero and zero respectively.
`N_(1),N_(2),N_(3)` and `N_(4)` are the number of nuclei of `A,B,X` and `Y` at any instant `t`.

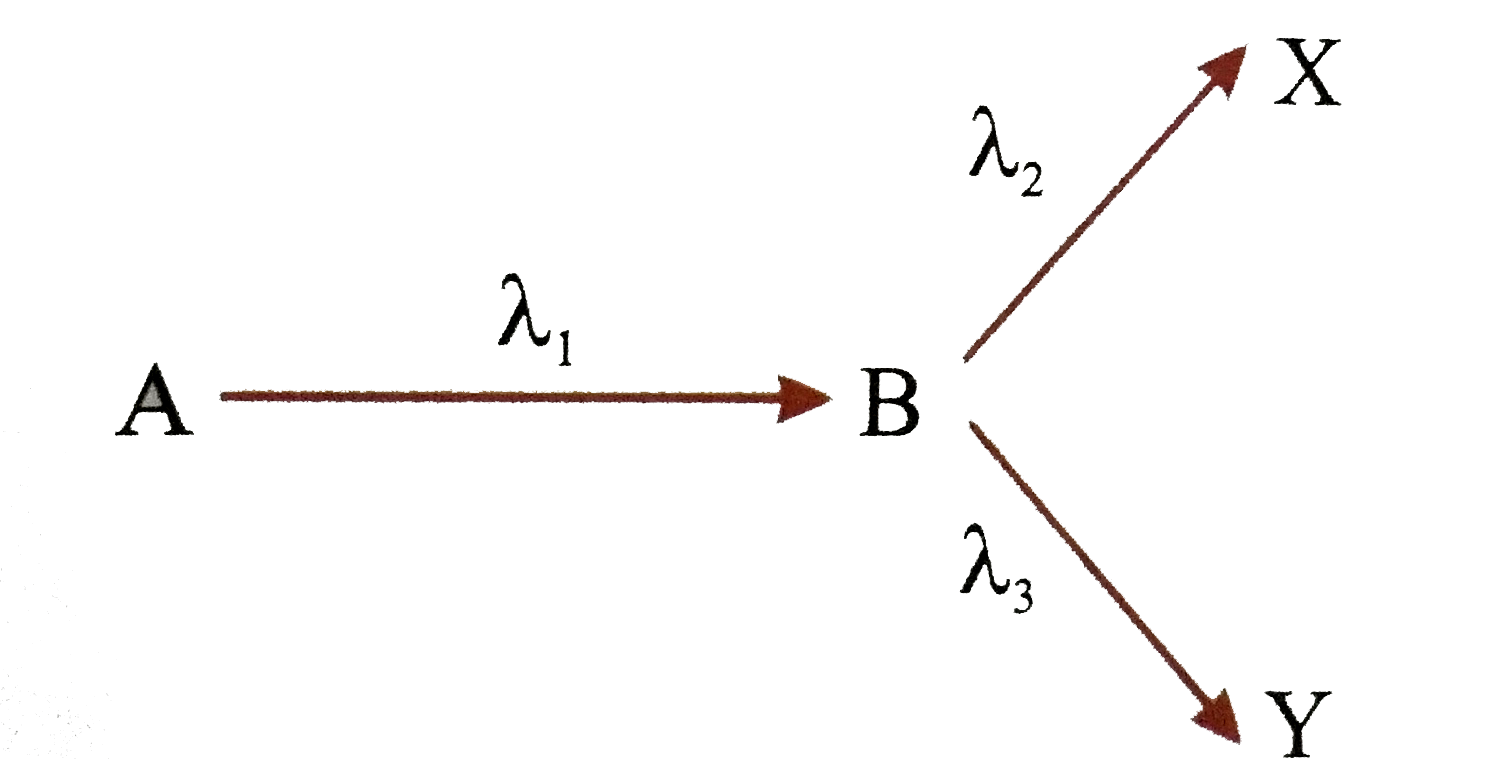
The number of nuclei of `B` will first increase and then after a maximum value, it decreases for

Consider radioactive decay of `A` to `B` with which further decays either to `X` or `Y`, `lambda_(1), lambda_(2)` and `lambda_(3)` are decay constant for `A` to `B` decay, `B` to `X` decay and Bto `Y` decay respectively. At `t=0`, the number of nuclei of `A,B,X` and `Y` are `N_(0), N_(0)` zero and zero respectively.
`N_(1),N_(2),N_(3)` and `N_(4)` are the number of nuclei of `A,B,X` and `Y` at any instant `t`.

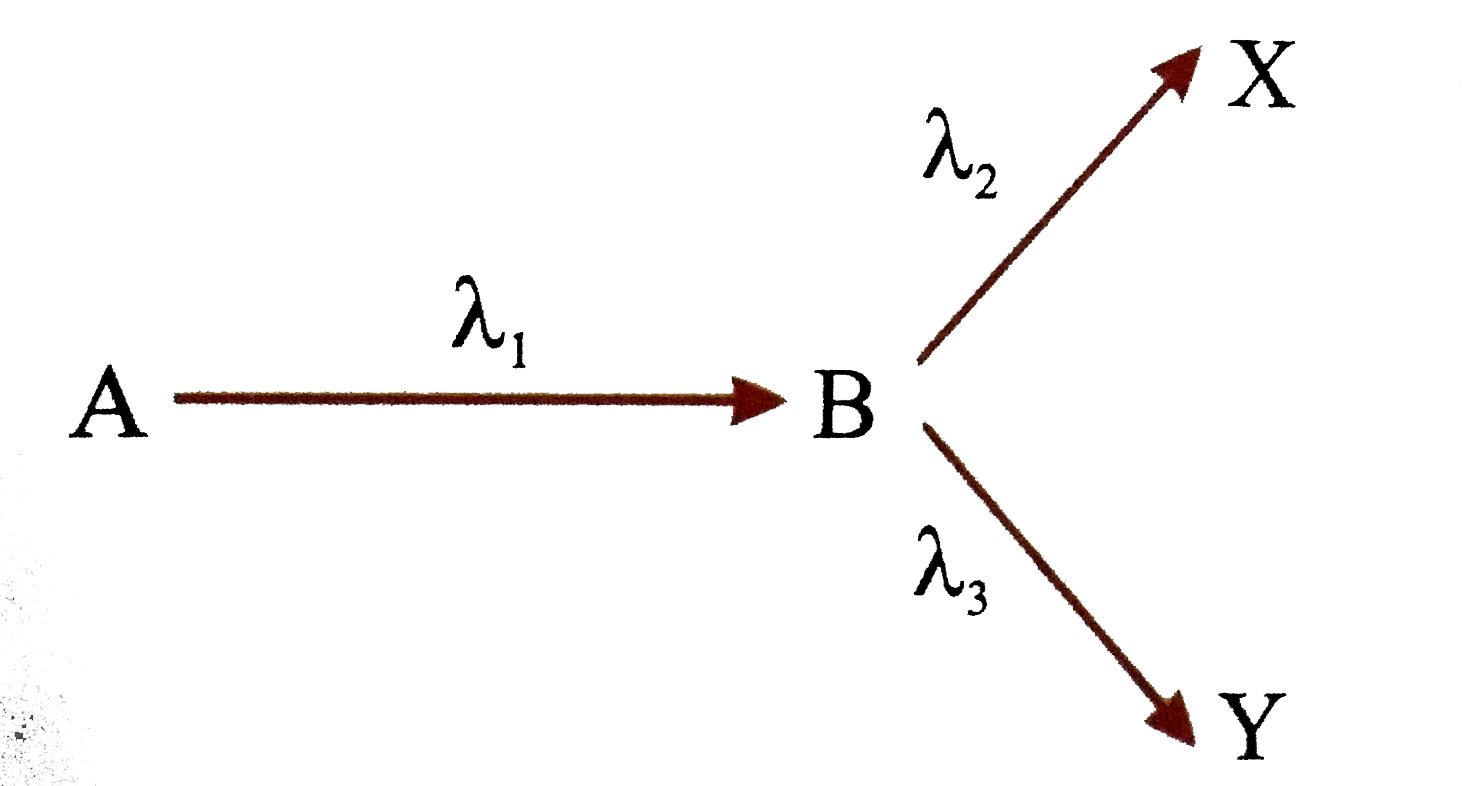
At `t=oo`, which of following is incorrect ?

Nuclei of a radioactive element `X` are being produced at a constant rate `K` and this element decays to a stable nucleus `Y` with a decay constant `lambda` and half-life `T_(1//3)`. At the time `t=0`, there are `N_(0) `nuclei of the element `X`.
The number `N_(X)` of nuclei of `X` at time `t=T_(1//2)` is .

Nuclei of a radioactive element `X` are being produced at a constant rate `K` and this element decays to a stable nucleus `Y` with a decay constant `lambda` and half-life `T_(1//3)`. At the time `t=0`, there are `N_(0) `nuclei of the element X.
The number `N_(Y)` of nuclei of `Y` at time `t` is .

Nuclei of a radioactive element `X` are being produced at a constant rate `K` and this element decays to a stable nucleus `Y` with a decay constant `lambda` and half-life `T_(1//3)`. At the time `t=0`, there are `N_(0) `nuclei of the element `X`.
The number `N_(Y)` of nuclei of `Y` at `t=T_(1//2)` is.

A town has a population of 1 million. The average electric power needed per person is 300W. A reactor is to be designed to supply power to this town. The efficiency with which thermal power is converted into electric power is aimed at 25%.(a) Assuming 200 MeV of thermal energy to come form each fission event on an average, find the number of events on an place every day. (b) Assuming the fission to take place largely through `U^235`, at what rate will the amount of `U^235` decrease ? Express uour answer in kg per day. (c) Assuming that uranium enriched to 3% in `U^235` will be used, how much uranium is needed per month (30 days)?

A town has a population of 1 million. The average electric power needed per person is 300W. A reactor is to be designed to supply power to this town. The efficiency with which thermal power is converted into electric power is aimed at 25%.(a) Assuming 200 MeV of thermal energy to come form each fission event on an average, find the number of events on an place every day. (b) Assuming the fission to take place largely through `U^235`, at what rate will the amount of `U^235` decrease ? Express uour answer in kg per day. (c) Assuming that uranium enriched to 3% in `U^235` will be used, how much uranium is needed per month (30 days)?

A town has a population of 1 million. The average electric power needed per person is 300W. A reactor is to be designed to supply power to this town. The efficiency with which thermal power is converted into electric power is aimed at 25%.(a) Assuming 200 MeV of thermal energy to come form each fission event on an average, find the number of events on an place every day. (b) Assuming the fission to take place largely through `U^235`, at what rate will the amount of `U^235` decrease ? Express uour answer in kg per day. (c) Assuming that uranium enriched to 3% in `U^235` will be used, how much uranium is needed per month (30 days)?

The nuclear charge (`Ze`) is non uniformlly distribute with in a nucleus of radius r. The charge density `rho(r)` (charge per unit volume) is dependent only on the radial distance r form the centre of the nucleus s shown in figure. The electric field is only along the radial direction.

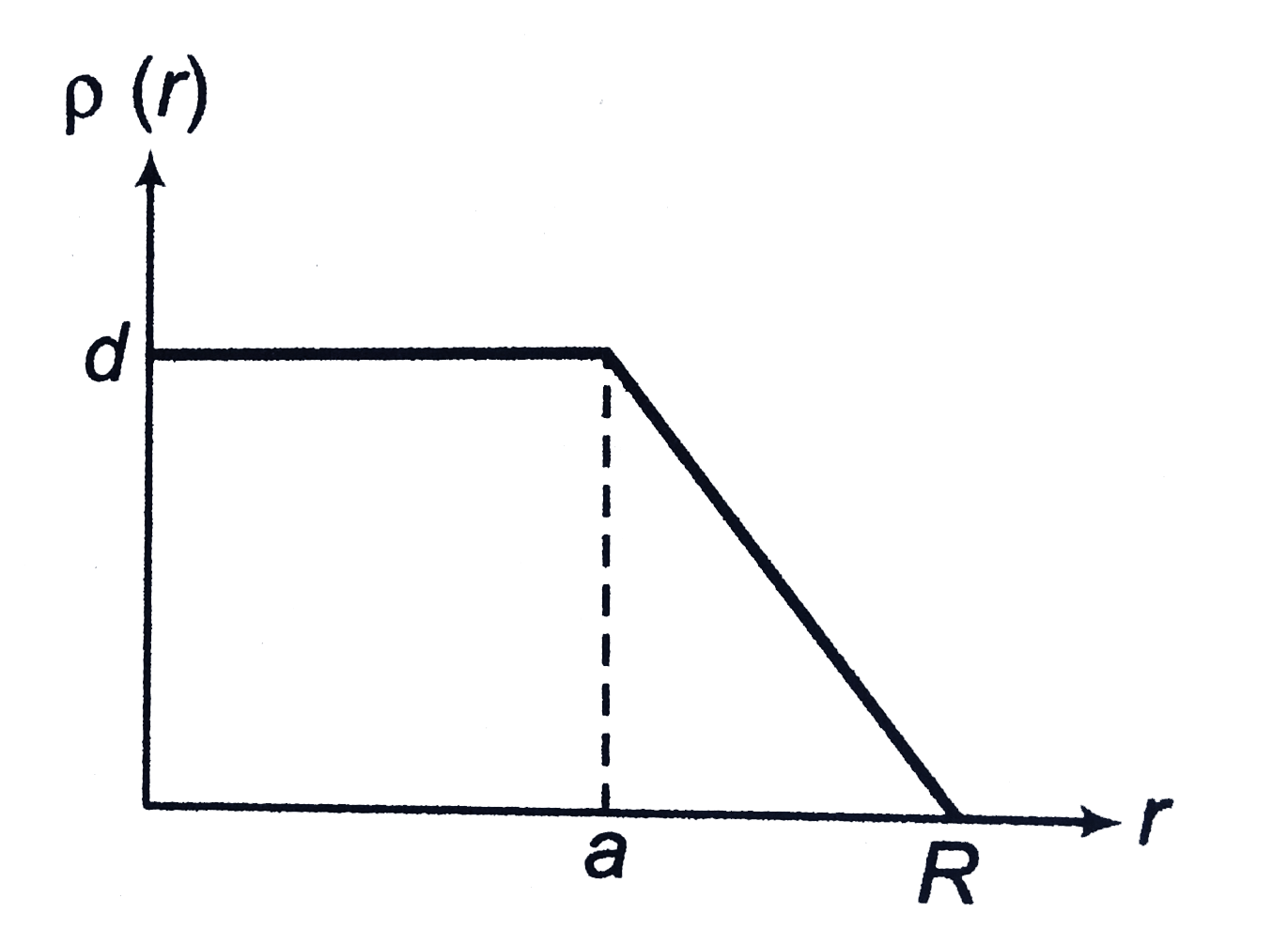
The electric field at `r=R` is

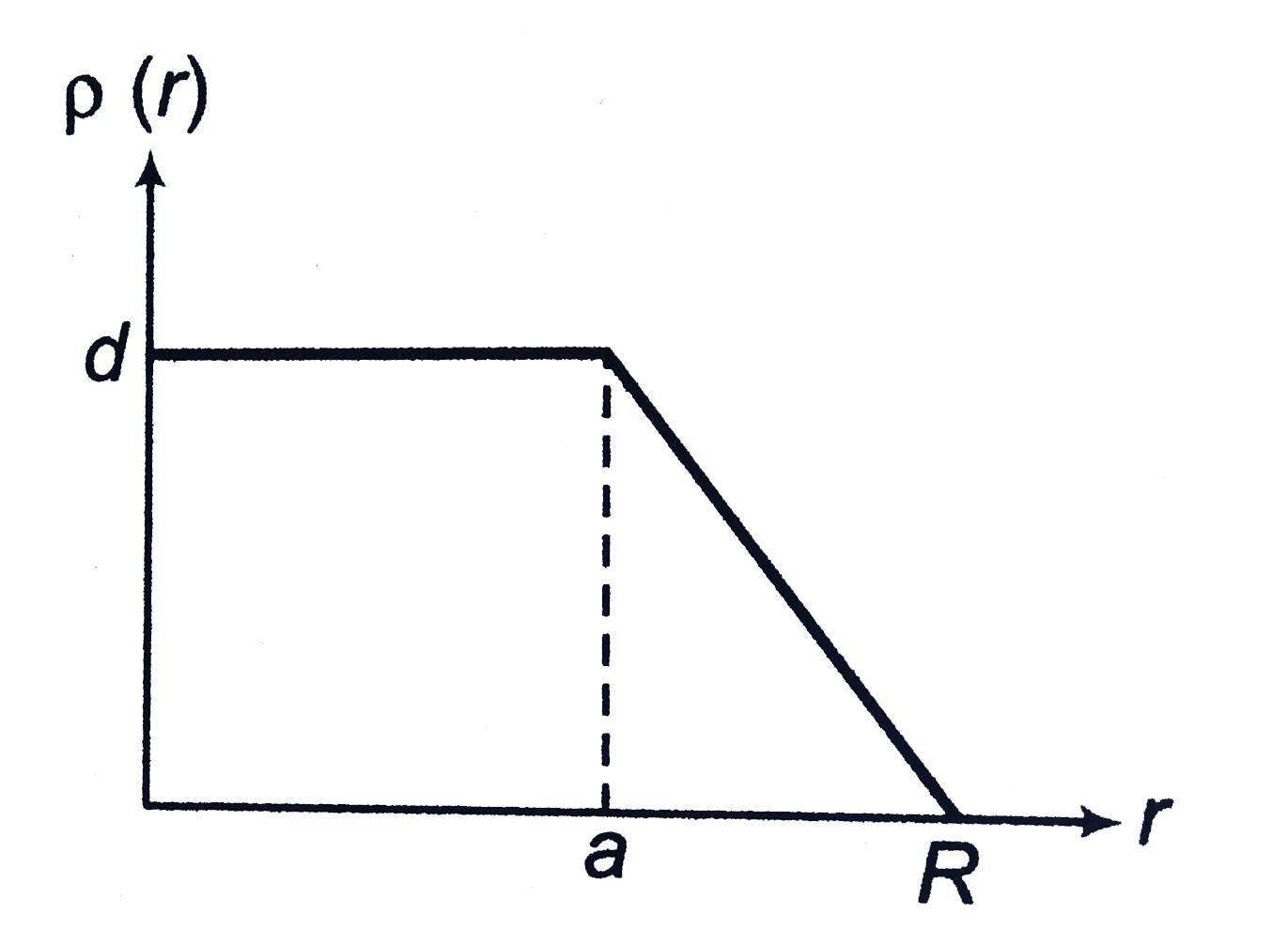
The nuclear charge (`Ze`) is non uniformlly distribute with in a nucleus of radius `r`. The charge density `rho(r)` (charge per unit volume) is dependent only on the radial distance r form the centre of the nucleus s shown in figure. The electric field is only along the radial direction.

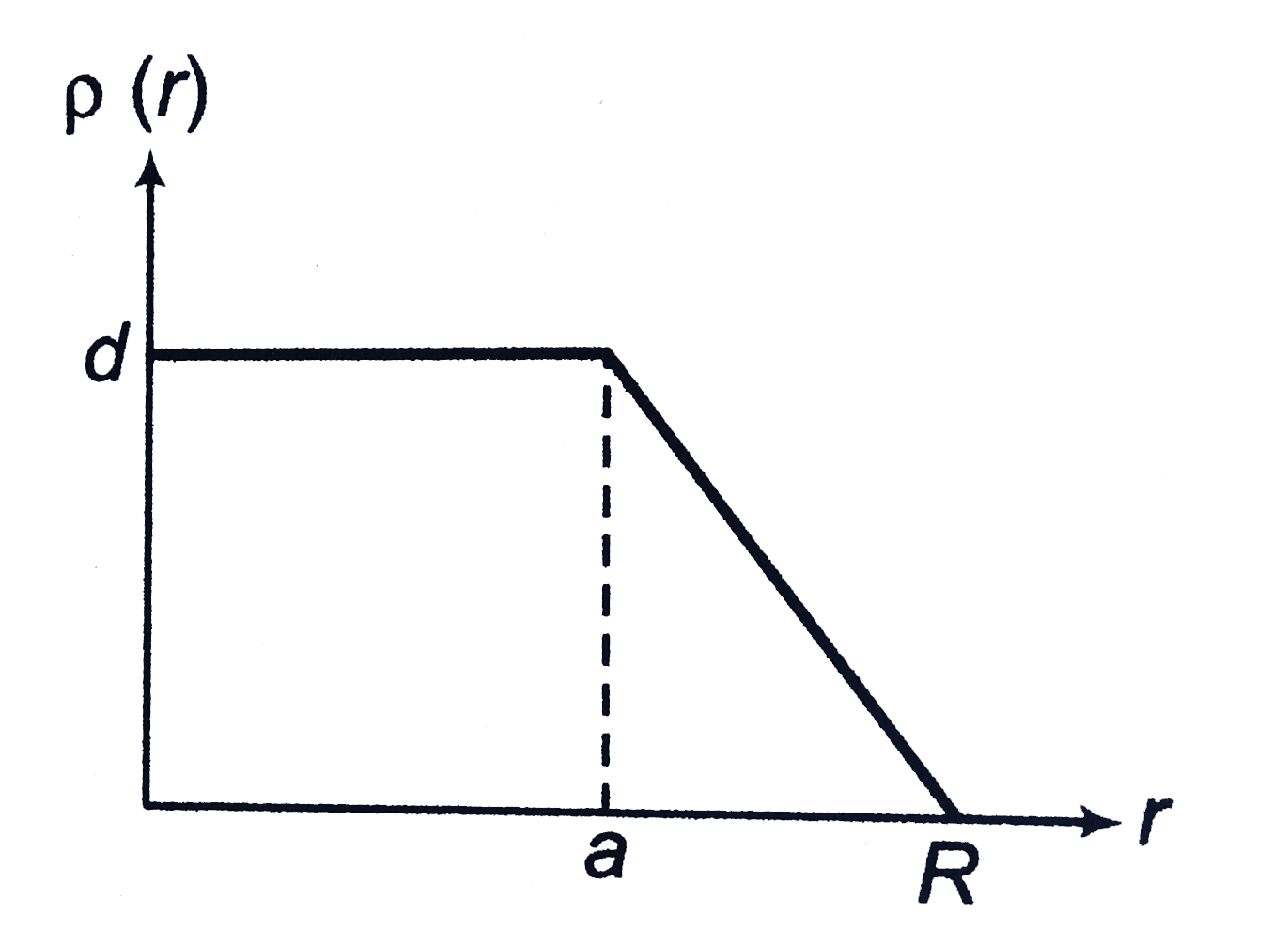
For a=0 the value of d (maximum value of `rho` as shown in the figure) is

Assume that the mass of nucleus is given by `M=Amp` where `A` is the mass number and `mp=1.00727 u`. The density of the matter in the nucleus is about `yxx10^(17)kg//m^(3)`. Then `y` is _______
(Take `R_(0)=1.5Fm`)

If `._(92)U^(238)` changes to `._(85)At^(210)` by a series of `alpha`-and `beta` -decays, the number of `alpha` and `beta`-decays undergone is .

At a given instant, there are `25%` undecayed radio-active nuclei in a sample. After `8 sec`, the number of undecayed nuclei reduced to `12.5%`. The time after which the number of undecayed unclei will further reduce to `6.25%` of the reduced number is ______sec

There are two radio-active nuclei `A` and `B`. `A` in an alfa-emitter while `B` is a beta-emitter, Their disintegration constant are in the ratio of `1:4`. The ratio of number of nuclei of `A` and `B` at any time `'t'` such that probabilities of getting number of alpha and beta particles are same at the instant is `y:1`. Then `y`______is

A small quantity of solution containing `Na^24` radio nuclide `(half-life=15 h)` of activity `1.0 microcurie` is injected into the blood of a person. A sample of the blood of volume `1cm^3` taken after `5h` shows an activity of `296` disintegrations per minute. Determine the total volume of the blood in the body of the person. Assume that the radioactive solution mixes uniformly in the blood of person.
(1 curie `=3.7 xx 10^10` disintegrations per second)

The radioactive of a sample is `R_(1)` at a time `T_(1)` and `R_(2)` at a time `T_(2)`. If the half-life of the specimen is `T`, the number of atoms that have disintegrated in the time `(T_(2)-T_(1))` is equal to`(n(R_(1)-R_(2))T)/(ln4) `. Here n is some integral number. What is the value of n?

In a nuclear reactor an element `X` decays to a radio active element `Y` at a constant rate `10^(15)` atoms per sec. Each decay release `100 MeV` energy. Half life of `Y` equals `T` and decays to a stable product `Z`. Each decay of `Y` releases `50 MeV`. All energy released inside the reactor is used to produce electricity at an afficiency of `25%`. Calculate the electrical power in `kw` generated in the reactor in steady state.

A charged capacitor of capacity `C` is discharge through a resistance `R`. A radioactive sample decays with an average life `J`. If the ratio of electrostatic field energy stored in the capacitor to the activity of the radioactive sample remains constant with time then `R=(xJ//C)`. where `x` is ________

A radio nuclide with half-life `T` days emits `beta`-particles of average kinetic energy `E J`. The radionuclide is used as a source in a machine which generates electric energy with efficiency `25%`. The number of moles of the nuclide required to generate electrical energy at an initial rate `P` is `n=(yTP)/(EN ln(2))` where `'y'` is

The average lifetime for the `n = 3` excited state of a hydrogen-like atom is `4.8 xx 10^(-8) s` and that for the `n = 2 state is 12.8 xx 10^(-8) s`. The ratio of average number of revolution made in the `n = 3` sate before any transition can take place from these state is.

In an `alpha` -decay, the kinetic energy of `alpha`-particles is `48 MeV` and `Q` value of the reaction is `50 MeV`. The mass number of the mother nucleus is (assume that daughter nucleus is in ground state)

Consider a nuclear reaction `A+B rarr C`. A nucleus `A` moving with kinetic energy of `5 MeV` collides with a nucleus `B` moving with kinetic energy of `3MeV` and forms a nucleus `C` in exicted state. Find the kinetic energy of nucleus `C` just after its fromation if it is formed in a state with excitation energy `10 MeV`. Take masses of nuclei of `A,B` and `C ` as `25.0,10.0,34.995 amu`, respectively.
(1amu=`930 MeV//c^(2))`.

`|Q|` value of the reaction, `N^(4)+alpha rarrO^(17)+p`
[the masses of `N^(14),He^(4),p,O^(17)` are respectively `14.00374 u, 4.0026 u,1.00783 u` and `16.99913 u` is `x//5MeV`. Value of `x` is nearly `[1 u=931.5 MeV]`

In a nucleus reactor `0.96` grams of `._(92)U^(235)` is consumed in one day. If `0.1%` of mass of `._(92)U^(235)` is available as energy fine the power of reactor (in `MW`)

The amount of heat generated by `1.0 mg` of a `Po^(210)` preparation during the one mean lifetime period of there nuclei, if the emitted a-particles are known to possess the kinetic energy `5.3 MeV` is `n(0.2 MJ)`. Assume all daughter nuclei are partically formed in ground state. What is the value of `n` ?