Complete Solutions to Solved Example of chapter NUCLEAR PHYSICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | NUCLEAR PHYSICS |
| NARAYANA | Solved Example |
| Number Of Questions | 32 |
| Academic Year | 2023-24 |
compare the radii of the nuclei of mass numbers `27` and `64`.
View SolutionThe radius of the oxygen nucleus `._(8)^(16)O` is `2.8 xx 10^(-15)m`. Find the radius of lead nucleus `._(82)^(205)Pb`.
View SolutionFind the binding energy of `._(26)^(56)Fe`. Atomic mass of `Fe` is `55.93 u` and that of Hydrogen is `1.00783 u` and mass of neutron is `1.00876 u`
View SolutionFind the energy required to split `._(8)^(16)O` nucleus into for `alpha` - particles. The mass of `alpha`- particle is `4.002603u` and that of oxygen is `15.994915 u`.
View SolutionCalculate the binding energy per nucleon of `._(20)^(40)Ca`. Given that mass of `._(20)^(40)Ca` nucleus `= 39.962589 u`, mass of proton `= 1.007825 u`. Mass of Neutron `= 1.008665 u` and `1 u` is equivalent to `931 MeV`.
View SolutionThe binding energies per nucleon for deuterium and helium are `1.1 MeV` and `7.0 MeV` respectively. What energy in joules will be liberated when `2` deuterons take part in the reaction.
View SolutionThe kinetic energy of `alpha`- particles emiited in the decay of `._(88)Ra^(226)` into `._(86)Rn^(222)` is measured to be `4.78 MeV`. What is the total disintegration energy or the `'Q'`-value of this process ?
View SolutionA nucleus X, initially at rest , undergoes alpha dacay according to the equation ,
` _(92)^(A) X rarr _(Z)^(228)Y + alpha `
(a) Find the value of `A` and `Z` in the above process.
(b) The alpha particle produced in the above process is found to move in a circular track of radius `0.11 m` in a uniform magnetic field of `3` Tesla find the energy (in MeV) released during the process and the binding energy of the parent nucleus X
Given that `: m (Y) = 228.03 u, m(_(0)^(1)n) = 1.0029 u. `
`m (_(2)^(4) He) = 4.003 u , m (_(1)^(1) H) = 1.008 u `
View SolutionThe nucleus `.^(23)Ne` deacays by `beta`-emission into the nucleus `.^(23)Na`. Write down the `beta`-decay equation and determine the maximum kinetic energy of the electrons emitted. Given,`(m(._(11)^(23)Ne) =22.994466 am u` and `m (._(11)^(23)Na =22.989770 am u`. Ignore the mass of antineuttino `(bar(v))`.
View SolutionCalculate the binding energy of an `alpha`-particles. Given that mass of proton`=1.0073u`, mass of neutron`=1.0087 u`. And mass of `alpha`-particle `=4.0015 u`.
View SolutionHow many `alpha` and `beta`-particles are emitted when uranium nucleus `(._(92)U^(238))` decay to `._(82)Pb^(214)`?
View SolutionA radioactive sample has an activity of `5.13xx10^(7)Ci`. Express its activity in 'becqueral' and 'rutherford'.
View SolutionA radioactive substance has `6.0xx10^(18)` active nuclei initially. What time is required for the active nuclei of the same substance to become `1.0xx10^(18)` if its half-life is `40s`.
View SolutionA radioactive nucleus can decay by two different processes. The half-life for the first process is `t_1` and that for the second process is `t_2`. Show that the effective half-life `t` of the nucleus is given by
`1/t = 1/t_1 + 1/t_2`.
View SolutionPlutonium decays with a half-life of `24000` years. If the plutonium is stored for `72000` years, then the fraction of plutonium that remains is.
View SolutionA certain substance decays to `1//32` of its initial activity in `25` days. Calculate its half-life.
View SolutionThe half-life period of a radioactive substance is `20` days. What is the time taken for `7//8th` of its original mass to disintergrate?
View SolutionHow many disintegrations per second will occur in one gram of `._92U^(238)`, if its half life against alpha decay is `1.42xx10^(17)s` ?
View SolutionOne gram of radium is reduced by `2` miligram in `5` yers by `alpha`-decay. Calculate the half-life of radium.
View SolutionThe half life of a radioactive substance is `5xx10^(3)`yrs. In how many years will its activity decay to 0.2 times its initial activity? Take `log_(10) 5=0.6990`.
View SolutionObtain the amount of `.^60Co` necessary to provide a radioactive source of `8.0 Ci` strength. The half-life of `.^60Co` is `5.3` years?
View SolutionAn explosion of atomic bomb releases an energy of `7.6xx10^(13)J`. If `200 MeV` energy is released on fission of one `.^(235)U` atom calculate (i) the number of uranium atoms undergoing fission. (ii) the mass of uranium used in the atom bomb
View SolutionCalculate the energy released by fission from `2 g` of `.^(235)._(92)U` in `kWh`. Given that the energy released per fission is `200 MeV`.
View SolutionIf `200 MeV` energy is released in the fission of a single `U^235` nucleus, the number of fissions required per second to produce `1` kilowatt power shall be (Given `1 eV = 1.6 xx 10^-19 J`).
View SolutionHow much `.^(235)U` is consumed in a day in an atomic powder house operating at `400 MW`, provided the whole of mass `.^(235)U` is converted into energy?
View SolutionHow long can an electric lamp of 100W be kept glowing by fusion of 2.0 kg of deuterium? The fusion reaction can be taken as `._1H^2+._1H^2to ._1H^3+n+3.17MeV`
View SolutionSuppose India has a target of producing by `2020 AD, 200,000 MW` of electric power, ten percent of which was to be obtained from nuclear power plants. Suppose we are given that, on an avedrage, the efficiency of utilization(i.e conversion to electric energy) of thermal energy produced in a reactor was `25%`. How much amount of fissionable uranium would our country need per year by `2020`? Take the heat energy per fission of `.^(235)U` to be about `200 MeV`.
View SolutionCalculate the energy released by the fission `1 g` of `.^(235)U` in joule, given that the energy released per fission is `200 MeV`.
(Avogadro's number `=6.023xx10^(23))`
View SolutionIn the process of nuclear fission of `1 g` uranium, the mass lost is `0.92 mg`. The efficiency of power house run by the fission reactor is `10%`.To obtain `400` megawatt power from the power house, how much uranium will be required per hour? `(c=3xx10^(8) m s^(-1))`.
View SolutionAn electron-positron pair is produced when a `gamma`-ray photon of energy `2.36 MeV` passes close to a heavy nucleus. Find the kinetic energy carried by each particle produced, as well as the total energy with each.
View SolutionA gamma ray photon of energy `1896 MeV` annihilates to produce a photon-antiproton pair. If the rest mass of each of the particles involved be `1.007276 a.m.u` aapproximately, find how much `K.E` these will carry?
View SolutionObtain the maximum kinetic energy of `beta`-particles, and the radiation frequencies of `gamma` decays in the decay scheme shown in Fig. `14.6`. You are given that `m(.^(198)Au)=197.968233 u, m(.^(198)Hg)=197.966760 u`
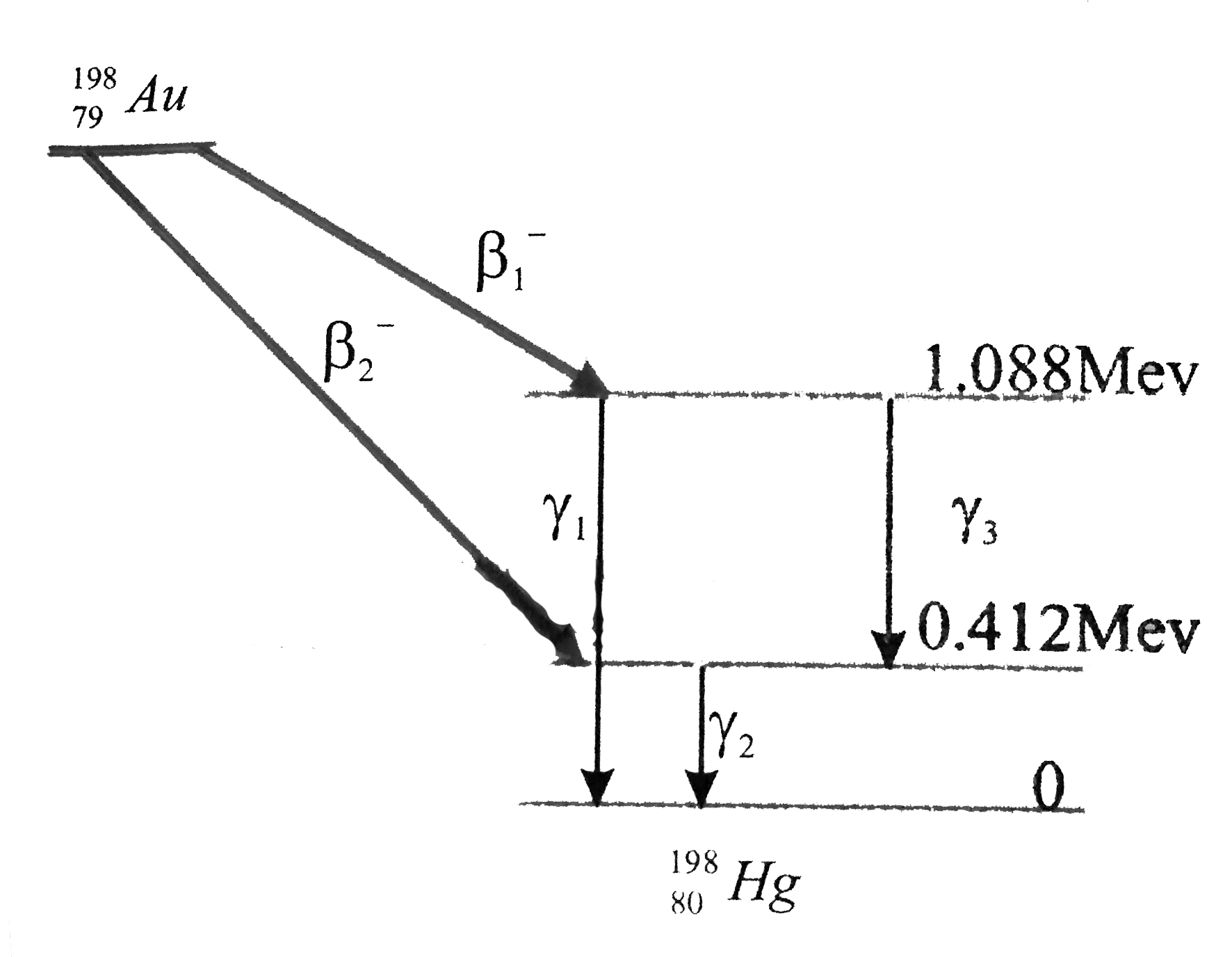
View Solution
Solved Example questions and complete solutions for chapter NUCLEAR PHYSICS of NARAYANA PHYSICS (HINGLISH) of Class 12