Complete Solutions to LEVEL - V of chapter WAVE OPTICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | WAVE OPTICS |
| NARAYANA | LEVEL - V |
| Number Of Questions | 37 |
| Academic Year | 2023-24 |
Two beam of light having intensities I and 4I interfere to produce a fringe pattern on a screen. The phase difference between the beams is `(pi)/(2)` at point A and `pi` at point B. Then the difference between resultant intensities at A and B is : `(2001 , 2M)`
View SolutionIn a double slit experiment, instead of taking slits of equal widths, one slit is made twice as wide as the other. Then, in the interference pattern
View SolutionIn a Young's double slit experiment, 12 fringes are observed to be formed in a certain segment of the screen when light of wavelength 600nm is used. If the wavelength of light is changed to 400nm, number of fringes observed in the same segment of the screen is given by
View SolutionIn a Young's double slit experiment, the separation between the two slits is d and the wavelength of the light is `lamda`. The intensity of light falling on slit 1 is four times the intensity of light falling on slit 2. Choose the correct choice (s).
View SolutionIn Young's double slit experiment intensity at a point is `((1)/(4))` of the maximum intersity. Angular position of this point is
View SolutionIn the Young's double slit experiment using a monochromatic light of wavelength `lamda`, the path difference (in terms of an integer n) corresponding to any point having half the peak
View SolutionTwo identical sources each of intensity `I_(0)` have a separation `d = lambda // 8`, where `lambda` is the wavelength of the waves emitted by either source. The phase difference of the sources is `pi // 4` The intensity distribution `I(theta)` in the radiation field as a function of `theta` Which specifies the direction from the sources to the distant observation point P is given by
View SolutionA screen is at distance `D = 80` cm form a diaphragm having two narrow slits `S_(1)` and `S_(2)` which are `d = 2` mm apart.
Slit `S_(1)` is covered by a transparent sheet of thickness
`t_(1) = 2.5 mu m` slit `S_(2)` is covered by another sheet of thikness
`t_(2) = 1.25 mu m` as shown if Fig. 2.52.
Both sheets are made of same material having refractive index `mu = 1.40`
Water is filled in the space between diaphragm and screen. Amondichromatic light beam of wavelength `lambda = 5000 Å` is incident normally on the diaphragm.
Assuming intensity of beam to be uniform, calculate ratio of intensity of C to maximum intensity of interference pattern obtained on the screen `(mu_(w) = 4//3)`

View SolutionIn figure S is a monochromatic point source emitting light of wavelength `lambda=500 nm`. A thin lens of circular shape and focal length `0.10 m` is cut into two identical halves `L_(1)` and `L_(2)` by a plane passing through a doameter. The two halves are placed symmetrically about the central axis `SO` with a gap of `0.5 mm`. The distance along the axis from `A` to `L_(1)` and `L_(2)` is `0.15 m`, while that from `L_(1)` and `L_(2)` to `O` is `1.30 m`. The screen at `O` is normal to `SO`.
(a) If the `3^(rd)` intensity maximum occurs at point `P` on screen, find distance `OP`.
(b) If the gap between `L_(1)` and `L_(2)` is reduced from its original value of `0.5 mm`, will the distance `OP` increases, devreases or remain the same?

View SolutionIn a modified YDSE, the region between the screen and slits is immersed in a liquid whose refractive index varies with time as `mu_(1) = (5 // 2) - (T // 4)` until it reaches s steady state value of `5 // 4`. A glass plate of thickness 36 `mu m` and refractive index `3//2` is introduced in front of one of the slits.
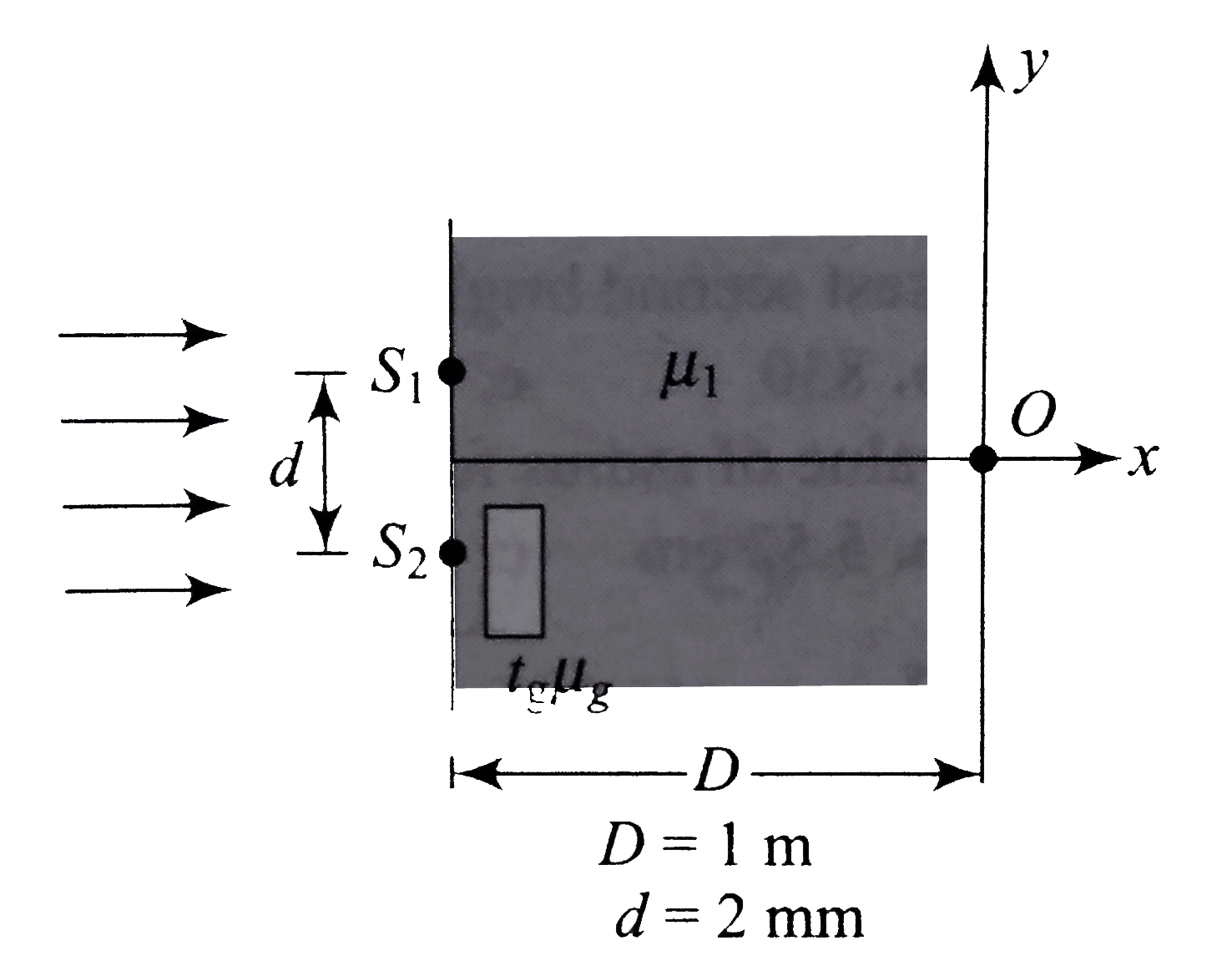
Find the time when central maxima is at point O. located symmetrically on the x-asix.
View SolutionIn the ideal double-slit experiment, when a glass-plate (refractive index 1.5) of thickness t is introduced in the path of one of the interfering beams (wavelength `lambda`), the intensity at the position where the central maximum occurred previously remains unchanged. The minimum thickness of the glass-plate is
View SolutionIn an interference arrangement similar to Young's double-slit experiment, the slits S_1 and S_2 are illuminated with coherent microwave sources, each of frequency 10^6 Hz. The sources are synchronized to have zero phase difference. The slits are separated by a distance d=150.0 m. The intensity I (theta) is measured as a function of theta, where theta is defined as shown. If I_0 is the maximum intensity, then I (theta) for 0lethetale90degree is given by

View SolutionIn YDSE, bichromatic light of wavelengths 400 nm and 560 nm
are used. The distance between the slits is 0.1 mm and the distance between the
plane of the slits and the screen is 1m. The minimum distance between two
successive regions of complete darkness is
View SolutionIntensity obseverd in an interferecne pattern is `I = I_(0) sin^(2) theta`. At `theta = 30^(@)`, Intensity `I = 5 +- 0.002`. The pecentage error in angle is
View SolutionWhite light is used to illuminate the two slits in a Young's double slit experiment. The separation between the slits is b and the screen is at a distance d`(gtb) from the slits. At a point on the screen directly in front of one of the slits, certain wavelength are missing. Some of these missing wavelength are
View SolutionTwo points nonochromatic and coherent sources of light of wavelength `lambda` each are placed as shown in figure. The initial phase difference between the sources is zero O. `(d gt gt d)`. Mark the correct statement(s).
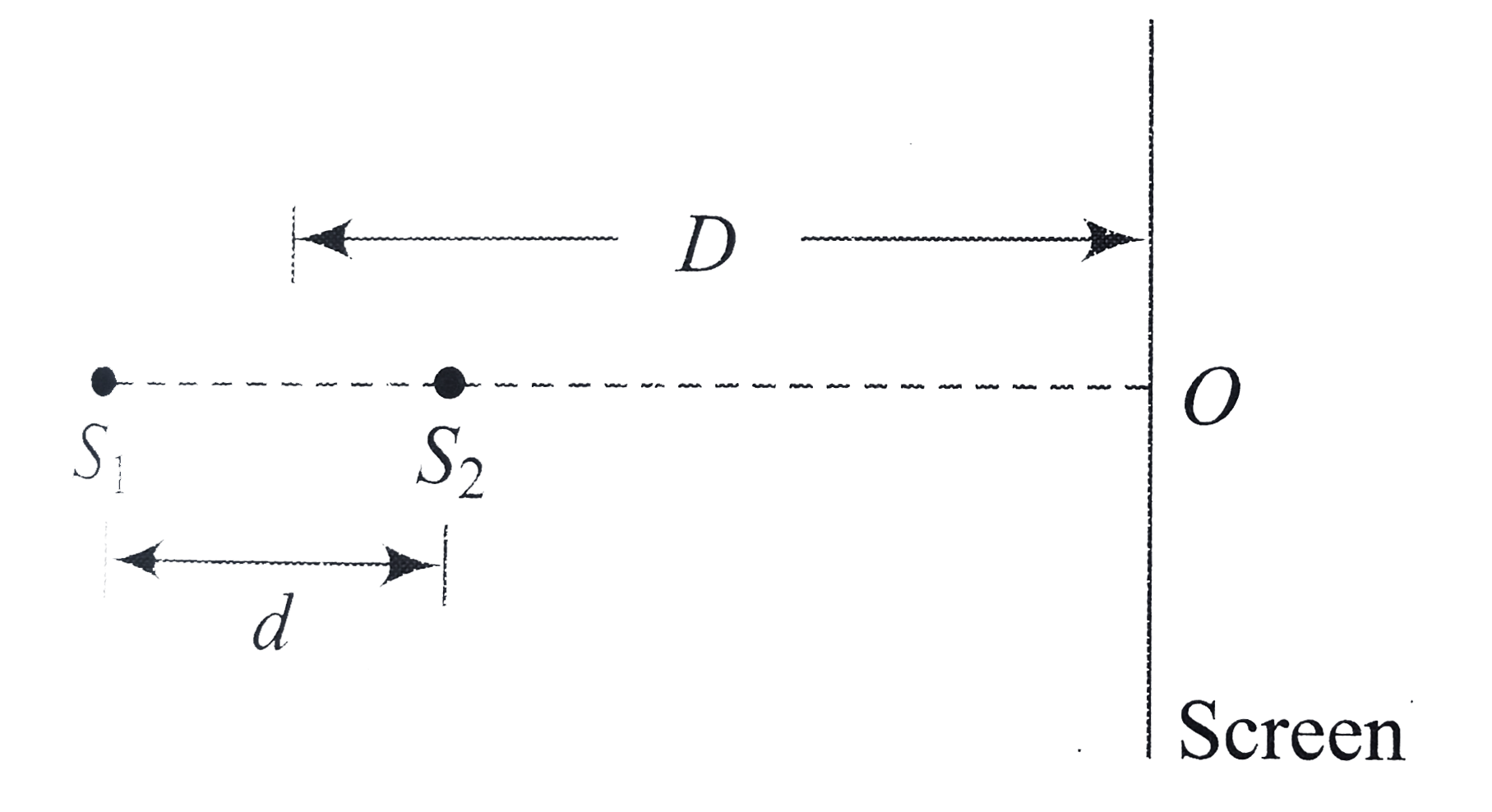
View SolutionThe minimum value of d os that there is a dark fringe at O is `d_(min)`. For the value of `d_(min)`, the distance at which the next bright fringe is formed is x. Then
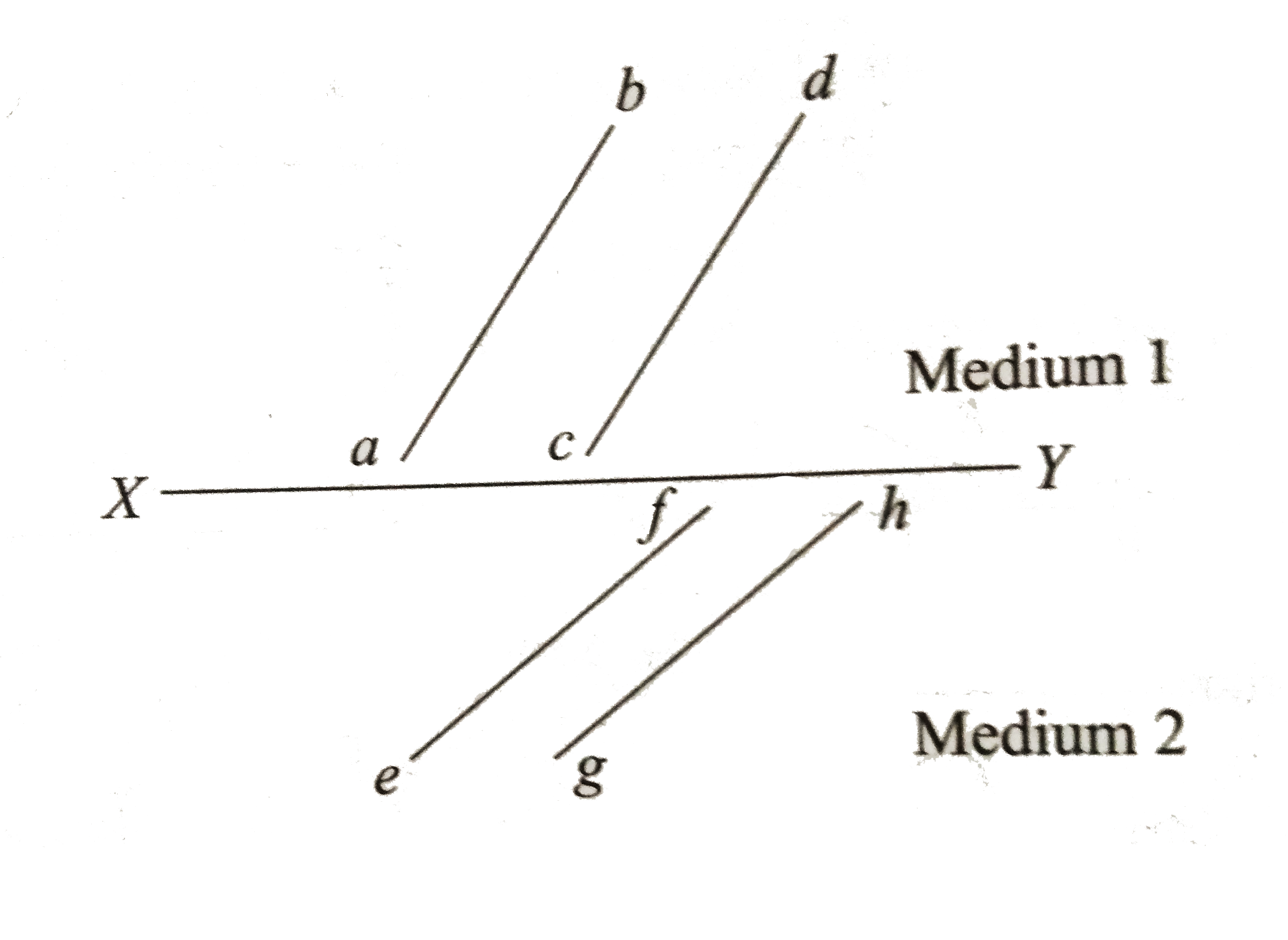
View SolutionFig. shows a surface XY separating two transparent media, medium 1 and medium 2. Lines ab and cd represent wavefronts of a light wave travelling in medium 1 and incident on XY. Line ef and gh represent wavefront of the light wave in medium 2 after rafraciton.

Light travel as a
View SolutionFig. shows a surface XY separating two transparent media, medium 1 and medium 2. Lines ab and cd represent wavefronts of a light wave travelling in medium 1 and incident on XY. Line ef and gh represent wavefront of the light wave in medium 2 after rafraciton.

The phase of the ligth wave at c, d, e, and f are `phi_(c)`, phi_(d), `phi_(e)` and `phi_(f)`, respectively. It is given that `phi_(c ) != phi_(f)`. Then
View SolutionFig. shows a surface XY separating two transparent media, medium 1 and medium 2. Lines ab and cd represent wavefronts of a light wave travelling in medium 1 and incident on XY. Line ef and gh represent wavefront of the light wave in medium 2 after rafraciton.
 Speed of light is
Speed of light is
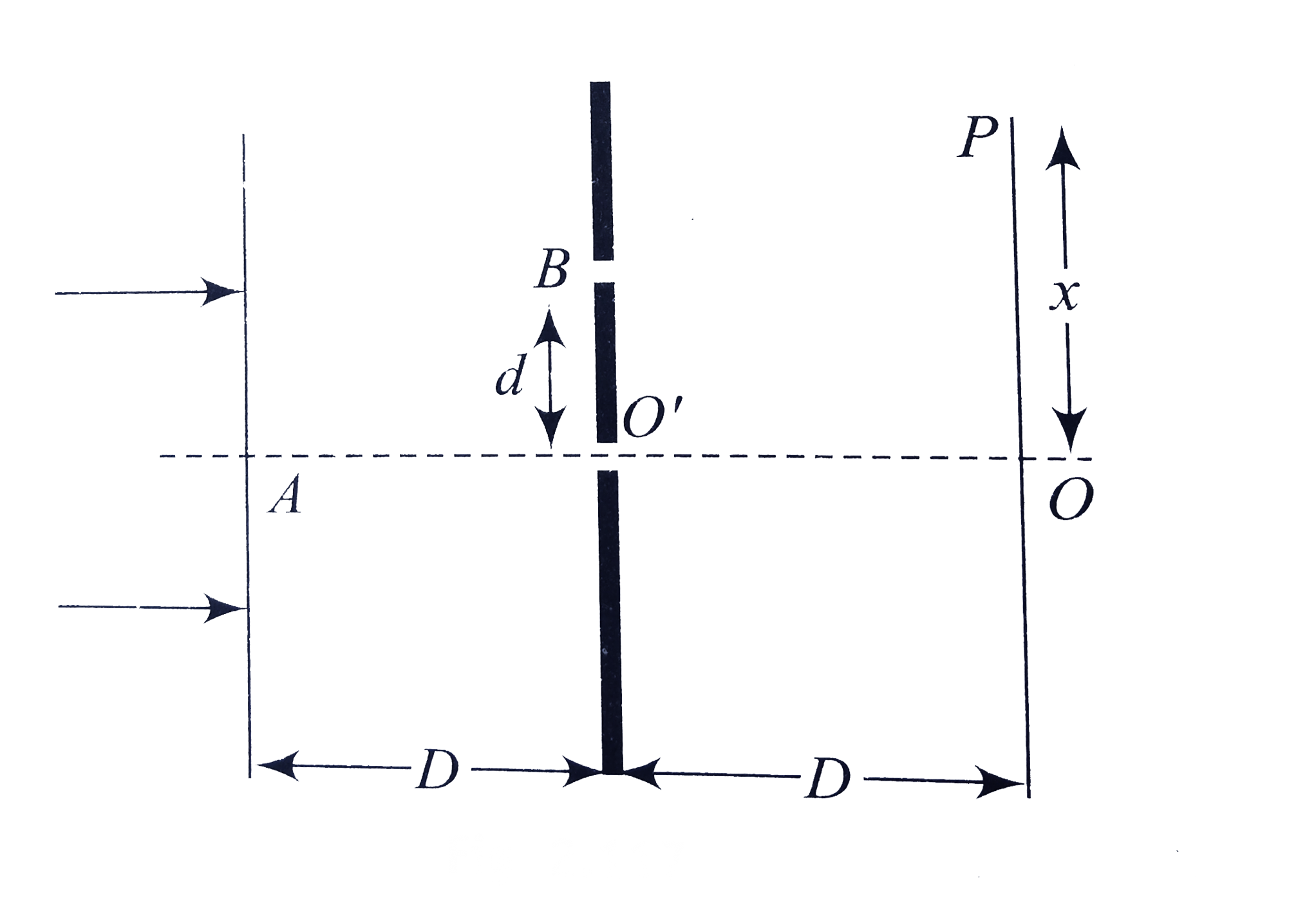
View SolutionIn the arrangement shown in Fig., slits `S_(1)` and `S_(4)`are having a variable separation Z. Point O on the screen is at the common perpendicular bisector of `S_(1) S_(2)` and `S_(3) S_(4)`.

When `Z = (lambda D)/(2d)`, the intensity measured at O is `I_(0)`. The intensity at O When `Z = (2 lambda D)/(d)` is
View SolutionIn the arrangement shown in Fig., slits `S_(1)` and `S_(4)`are having a variable separation Z. Point O on the screen is at the common perpendicular bisector of `S_(1) S_(2)` and `S_(3) S_(4)`.
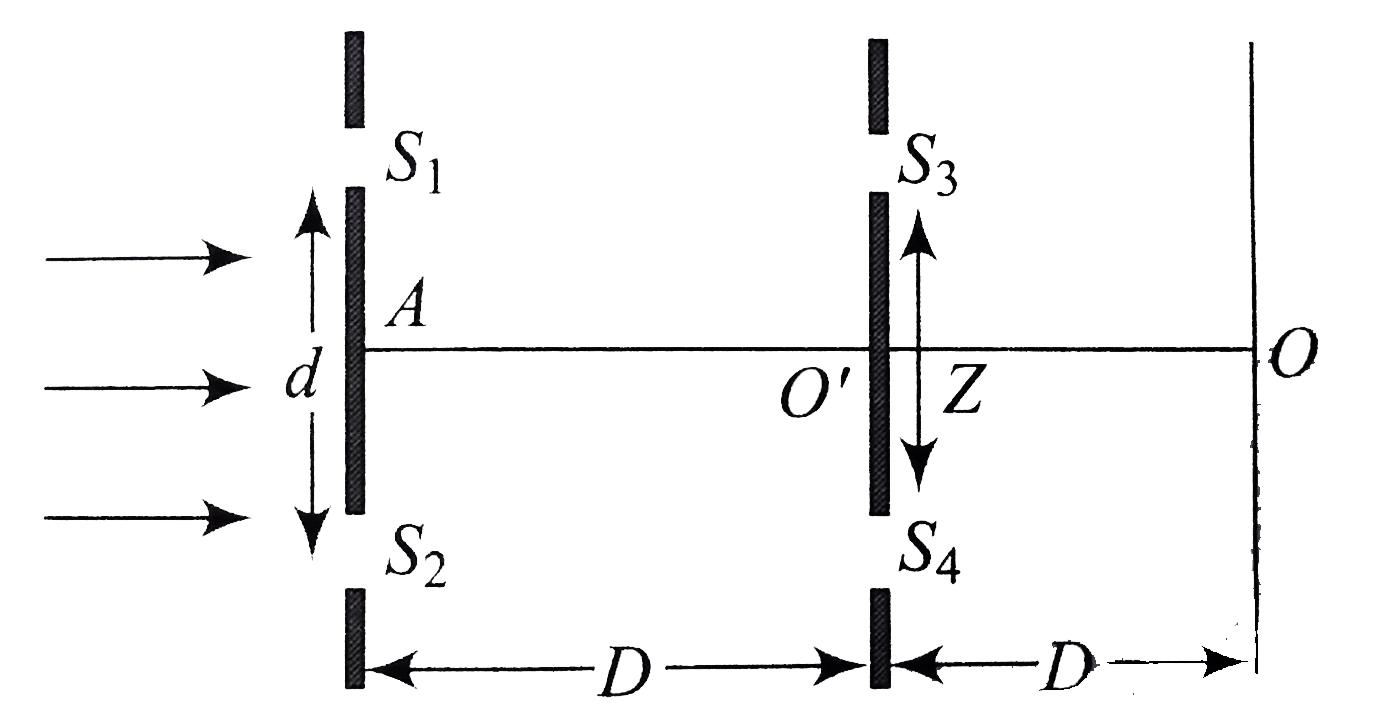
The minimum value of Z for which the intensity at O is zero is
View SolutionIn the arrangement shown in Fig., slits `S_(1)` and `S_(4)`are having a variable separation Z. Point O on the screen is at the common perpendicular bisector of `S_(1) S_(2)` and `S_(3) S_(4)`.
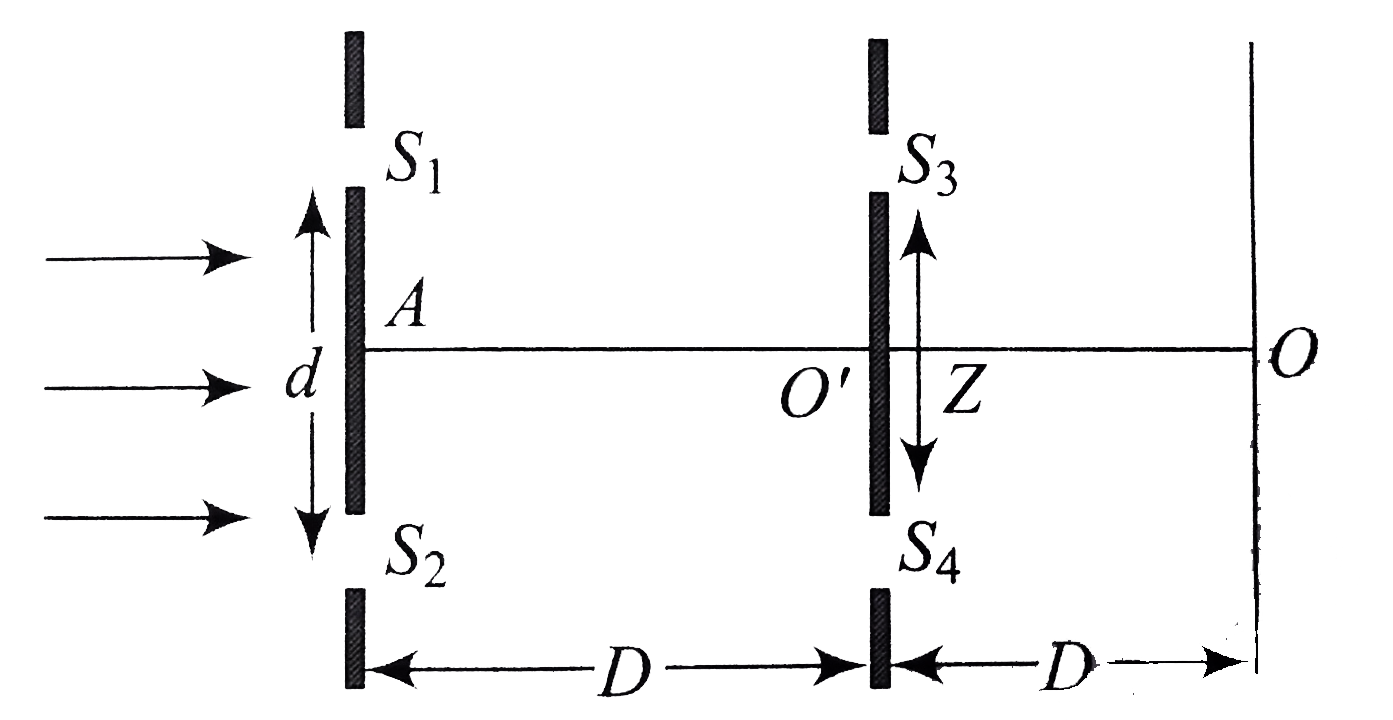
If a hole is made at O' on AO' O and the slit `S_(4)` is closed, then the ratio of the maximum to minimum observed on screen at O , if `O' S_(3)` is equal to `(lambda D)/(4d)`, is
View SolutionA monochromatic beam of light fall on YDSE apparatus at some angle (say `theta`) as shown in figure. A thin sheet of glass is inserted in front of the lower slit `s_(2)`. The central bright fringe (path difference `= 0`) will be obtained
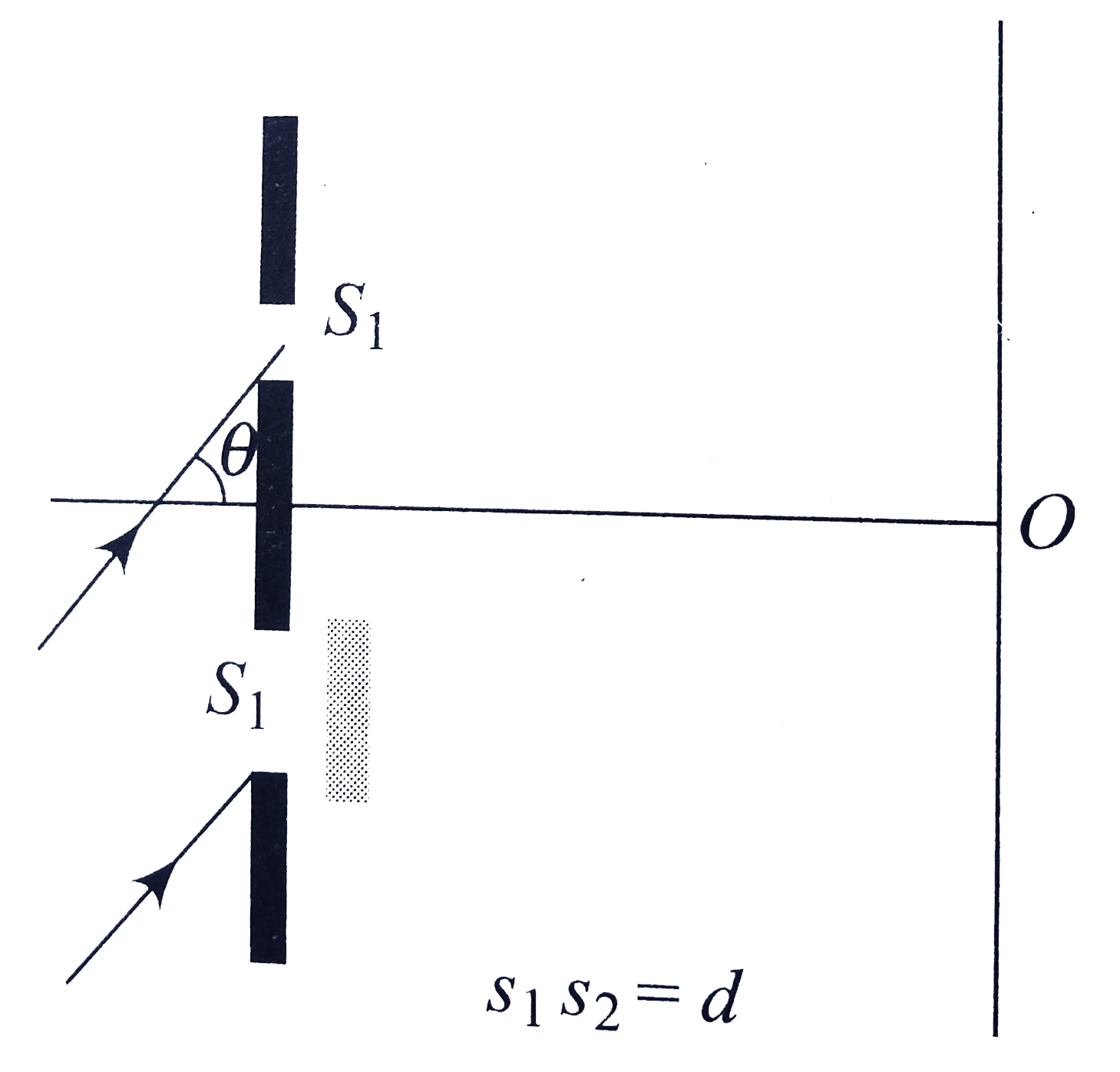
View SolutionA monochromatic beam of light falls on Young's double slit experiment apparatus as shown in figure. A thin sheet of glass is inserted in front of lower slit `S_(2) (lambda = 600 nm` is wavelength of source)

If central bright fringe is obtained on screen at 'O' then
View SolutionA monochromatic beam of light falls on Young's double slit experiment apparatus as shown in figure. A thin sheet of glass is inserted in front of lower slit `S_(2) (lambda = 600 nm` is wavelength of source)

The phase difference between central masxima and 5th minima is
View SolutionWave property of electron implies that they will show diffraction effected . Davisson and Germer demonstrated this by diffracting electron from crystals . The law governing the diffraction from a crystals is obtained by requiring that electron waves reflected from the planes of atoms in a crystal interfere constructiely
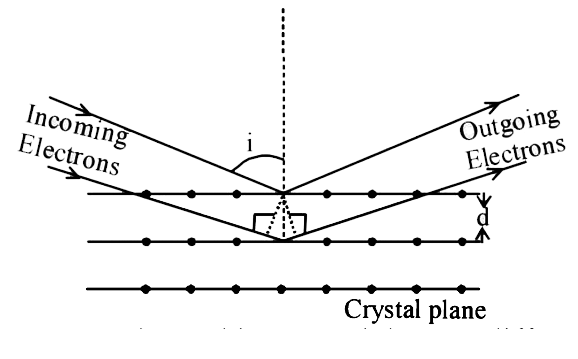
Electron accelerated by potential `V` are diffracted from a crystal if `d = 1 Å and i = 30^(@), V` should be about `(h = 6.6 xx 10^(-34) Js, m_(e) = 9.1 xx 10^(-31) kg , e = 1.6 xx 10^(-19)C)`
View SolutionWave property of electron implies that they will show diffraction effected . Davisson and Germer demonstrated this by diffracting electron from crystals . The law governing the diffraction from a crystals is obtained by requiring that electron waves reflected from the planes of atoms in a crystal inter fere constructiely
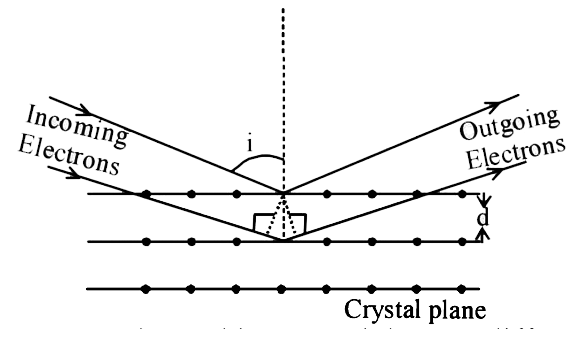
If a strong diffraction peak is observed when electrons are incident at an angle `i` from the normal to the crystal planes with distance `d` between them (see fig) de Brogle wavelength `lambda_(dB)` of electrons can be calculated by the relationship (n is an intenger)
View SolutionWave property of electrons implies that they will show diffraction effects. Davission and Germer demonstrated this by diffracting electrons from crystals. The law governing the diffraction from a crystal is obtained by requiring that electron waves reflected from the planes of atoms in a crystal interfere constructively (see figure)

In an experiment, electrons are made to pass through a narrow slit of width 'd' comparable to either de-Broglie wavelength. They are detected on a screen at a distance 'D' from the slit

The following graphs that can be expected to represent the number of electrons 'N' detected as a function of the detector position 'y' (`y=0` corresponds to the middle of the slit) is
View SolutionA Young's double slit experiment is conducted with slit separation 10mm, where the screen is 2m away from the slits. If wavelength of light used is `6000 Å` , answer the following
Fringe width in mm is
View SolutionA Young's double slit experiment is conducted with slit separation 10mm, where the screen is 2m away from the slits. If wavelength of light used is `6000 Å` , answer the following
distance of 4th dark band from central fringe in mm is
View SolutionA Young's double slit experiment is conducted with slit separation 10mm, where the screen is 2m away from the slits. If wavelength of light used is `6000 Å` , answer the following
If the wavelength is increased by `1000 Å` , and the whole apparatus is placed in water of refractive index `4//3` , the new fringe width in mm is
View SolutionAn inteference is observed due to two coherent sources A and B separated by a distance `4lambda` along Y-axis, where `lambda` is the wavelength of light. A detector 'D' is moved alog the positive X-axis. Find the totla number of maxima observe on the X-axis excluding the points `x =0` and `x = oo` ?

View SolutionTwo coherent light sources, each of wavelength `lambda`, are separated by a distance `3 lambda`, The maximum number of minima formed on line AB, which funs from `-oo` to `+oo`, is

View SolutionIn Young's experiment inteference bands are produced on the screen placed at `1.5m` from the slits `0.15mm` apart and illuminated by light of wavelength `6000 Å`. If the scren is now taken away from the slit by 50 cm the change in the fringe width will be
View SolutionIn YDSE, the sources is red ligth of wavelength `7 xx 10^(-7) m`. When a thin glass plate of refractive index 1.5 is put in the path of one of the interfering beams, the central bright fringe shifts by `10^(-3)` m to the position previously occupied by the 5th bright fringe.
What is the thickness of the plate?
View SolutionIn a modified Young's double-slit experiment, a monochromatic uniform and parallel beam of light of wavelength `6000 Å` and intensity `(10//pi)` W `m^(-2)` is incident normally on two circular apertures A and B of radii 0.001 m and 0.002 m, respectively. A perfectly transparent film of thickness `2000 Å` and refractive index 1.5 for the wavelength of `6000 Å` is placed in front of aperture A (see the figure). Calculate the power (in mW) received at the focal spot F of the lens. Then lens is symmetrically placed with respect to the aperture. Assume that 10% of the power received by each aperture goes in the original direction and is brought to the focal spot.
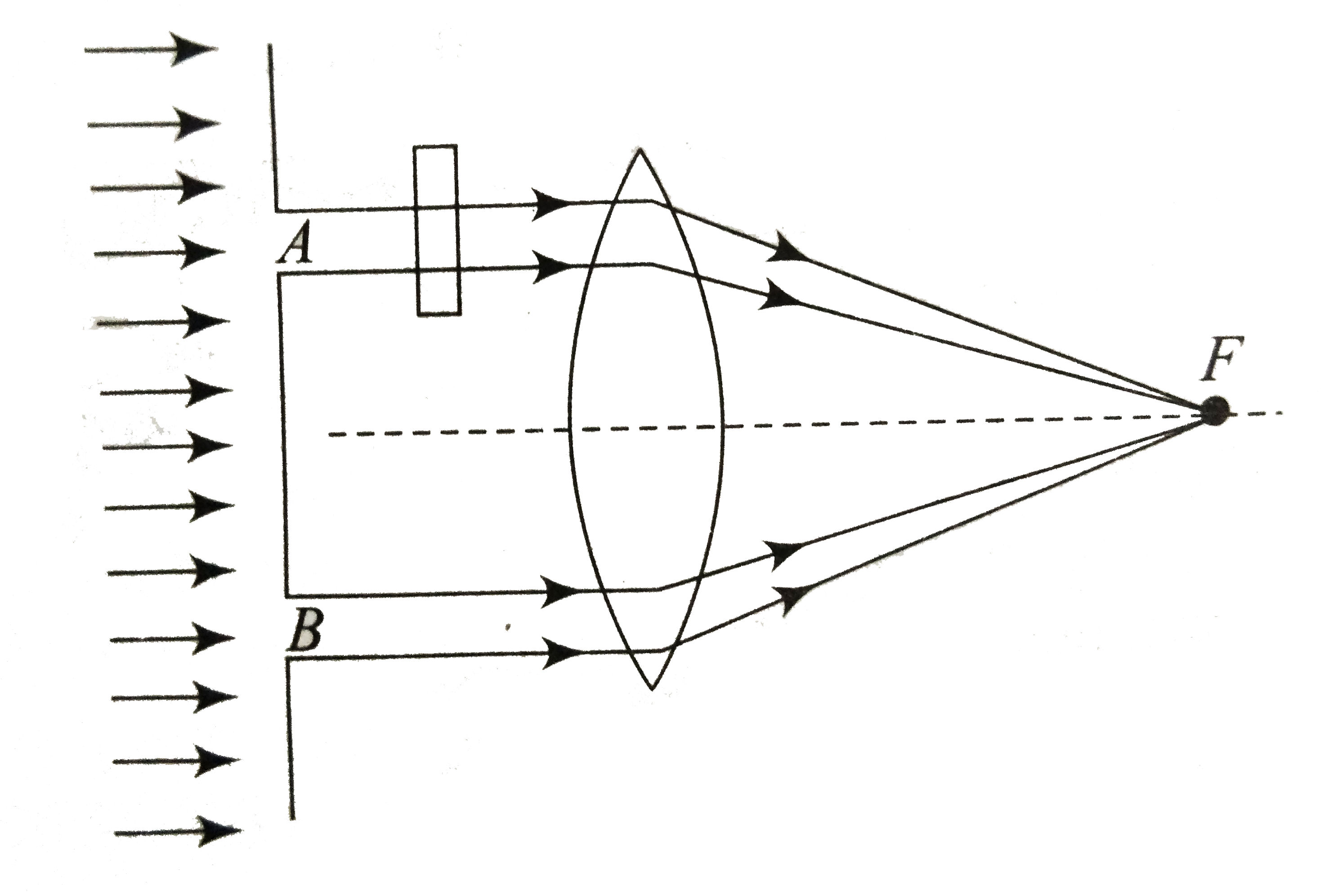
View Solution
LEVEL - V questions and complete solutions for chapter WAVE OPTICS of NARAYANA PHYSICS (HINGLISH) of Class 12
All Exercises from NARAYANA Class 12 PHYSICS WAVE OPTICS
- C . U . Q (Diffraction light)
- C . U . Q (interference)
- C . U . Q (Polarisation)
- C . U . Q (Resolving power)
- C.U.Q
- Evaluate yourself - 1
- Evaluate yourself - 2
- Evaluate yourself - 3
- Example
- Exercise - 1 (C.W) Huygen. s principle
- Exercise - 1 (C.W) Interference
- Exercise - 1 (C.W) Diffraction
- Exercise - 1 (C.W) Resolving power
- Exercise - 1 (C.W) Polarisation
- Exercise - 1 (C.W) Diffraction
- Exercise - 1 (H.W) Diffraction
- Exercise - 1 (H.W) Interference
- Exercise - 1 (H.W) Polarisation
- Exercise - 1 (H.W) Resolving power
- Exercise - 2 (C . W) Diffraction
- Exercise - 2 (C . W) Polarisation
- Exercise - 2 (C . W) Resolving power
- Exercise - 2 (C . W) Interference
- Exercise - 2 (H. W) Diffraction
- Exercise - 2 (H. W) Interference
- Exercise - 2 (H. W) Polarisation
- Exercise - 3
- Exercise - 4 Diffraction
- Exercise - 4 Interference of light
- Exercise - 4 Polarisation
- Exercise -1 (C.W) Diffraction
- Exercise -1 (C.W) Resolving power
- Exercise -1 (C.W) Huygen. s principle
- Exercise -1 (C.W) Huygen. s principle
- LEVEL - I (C.W)
- LEVEL - I(H.W)
- LEVEL - II (C.W)
- LEVEL - II(H.W)
- LEVEL - III
- LEVEL - V
- LEVEL - VI
- NCERT Based Questions