Complete Solutions to LEVEL - VI of chapter WAVE OPTICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | WAVE OPTICS |
| NARAYANA | LEVEL - VI |
| Number Of Questions | 40 |
| Academic Year | 2023-24 |
If two coherent source are placed at a distance `3lambda` from each other, symmetric to the centre of the circel as shown in figure, Find thenumber of fringes shown on the screen, placed along the circumference ?

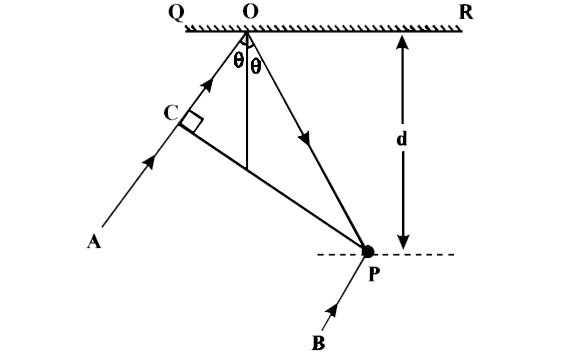
View SolutionIn the adjacent diagram, CP represents a wavefront and AO & BP, the corresponding two rays. Find the condition on `theta` for constructive interference at P between the ray BP and reflected ray OP.
View SolutionIn standard YDSE slits were moved apart symmetrically with relative velocity v, calculate the rate at which fringes pass a point at a distance x from the centre of the fringe system formed on a screen at 'y' distance away from the double slits if wavelength of light is `lambda` , and distance between the slits is 'b' . Assuming `y gtgt b & b gtgt lambda`
View SolutionABC is a spherical wavefront centred at 'O' symmetric about BE is incident on slits `S_(1)` and `S_(2)` . `BS_(1) = 3lambda , S_(1)S_(2) = 4 lambda , BO = 6lambda , S_(1)E = 128 lambda` and `lambda` is the wavelength of incident light wave. A mica sheet of refractive index `1.5` is pated on `S_(2)`. Find the minimum value of thickness of mica sheet for whhich central fringe forms at E ?

View SolutionA glass of refractive index 1.5 is coated with a thin layer of thickness t and refractive index 1.8 . Light of wavelength `lambda` travelling in air is incident normally on the layer. It is partly reflected at the upper and the lower surfaces of the layer. It is partly reflected at the upper and the lower surfaces of the layer ant the two reflected rays interface . If `lambda = 648 nm`, obtain the least value of `t ("in" 10^(-8)m )` which the rays interface constructively.
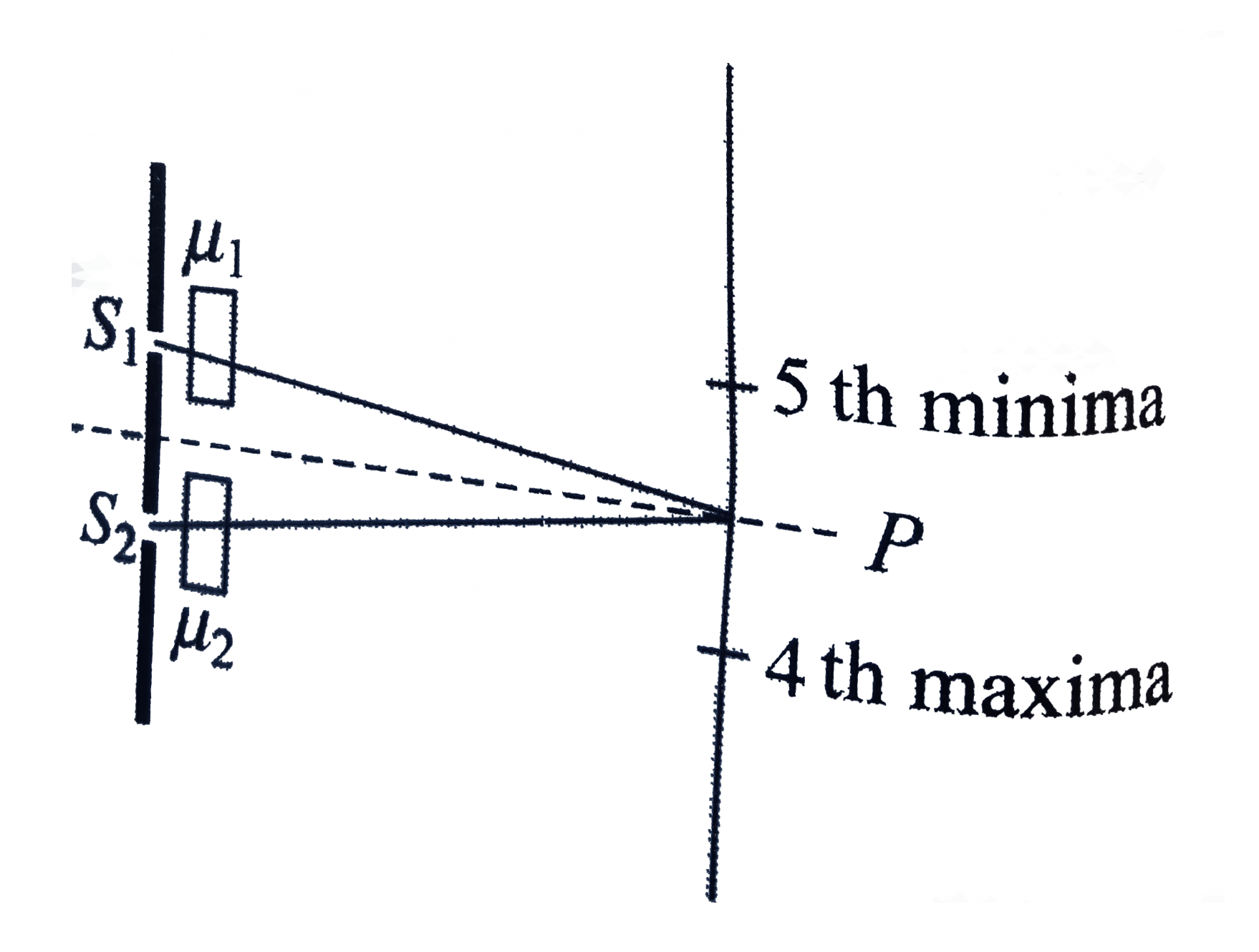
View SolutionIn Young's experiment the upper slit is covered by a thin glass plate of refractive index `1.4` while the lower slit is covered by another glass plate, having the same thickness as the first one but having refractive index `1.7` interference pattern is observed using light of wavelength `5400 Å`
It is found that point P on the screen where the central maximum `(n = 0)` fell before the glass plates were inserted now has `3//4` the original intensity. It is further observed that what used to be the fourth maximum earlier, lies below point P while the fifth minimum lies above P.
Calculate the thickness of glass plate. (Absorption of light by glass plate may be neglected.
 .
.
View SolutionIn a young's double slit experiment, two wavelength of 500 nm and 700 nm were used. What is the minimum distance from the central maximum where their maximas coincide again ? Take `D//d = 10^(3)` . Symbols have their usual meanings.
View SolutionIn a standard YDSE setup if the screen is kept tilted as shown, find the distance OA if first maximum is formed at A. Wavelength of light emitted by source is `lambda`

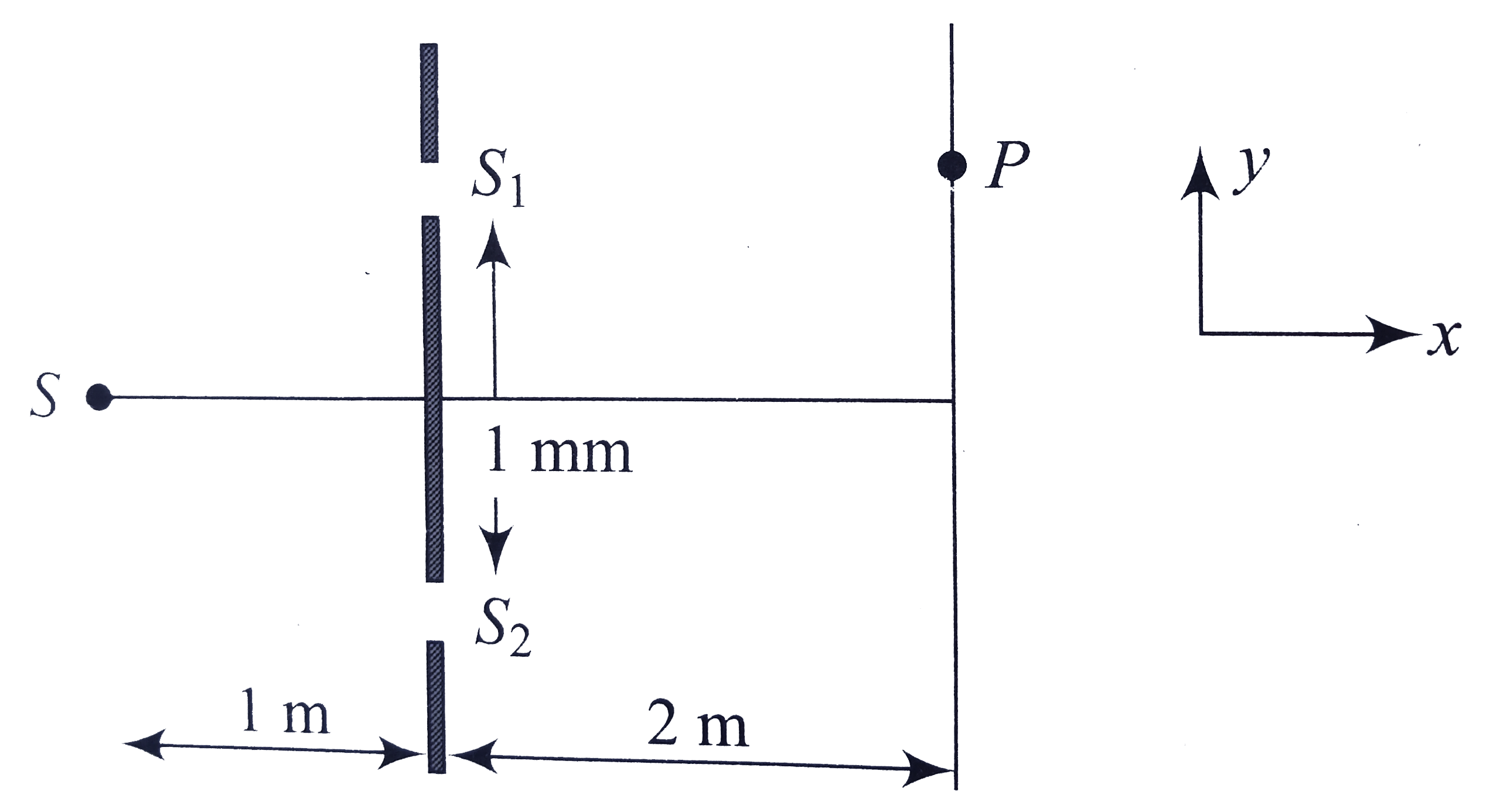
View SolutionIn young's double-slit experiment set up, sources S of wavelength 50 nm illumiantes two slits `S_(1)` and `S_(2)` which act as two coherent sources. The sources S oscillates about its own position according to the equation `y = 0.5 sin pi t`, where y is in nm and t in seconds. The minimum value of time t for which the intensity at point P on the screen exaclty in front of the upper slit becomes minimum is
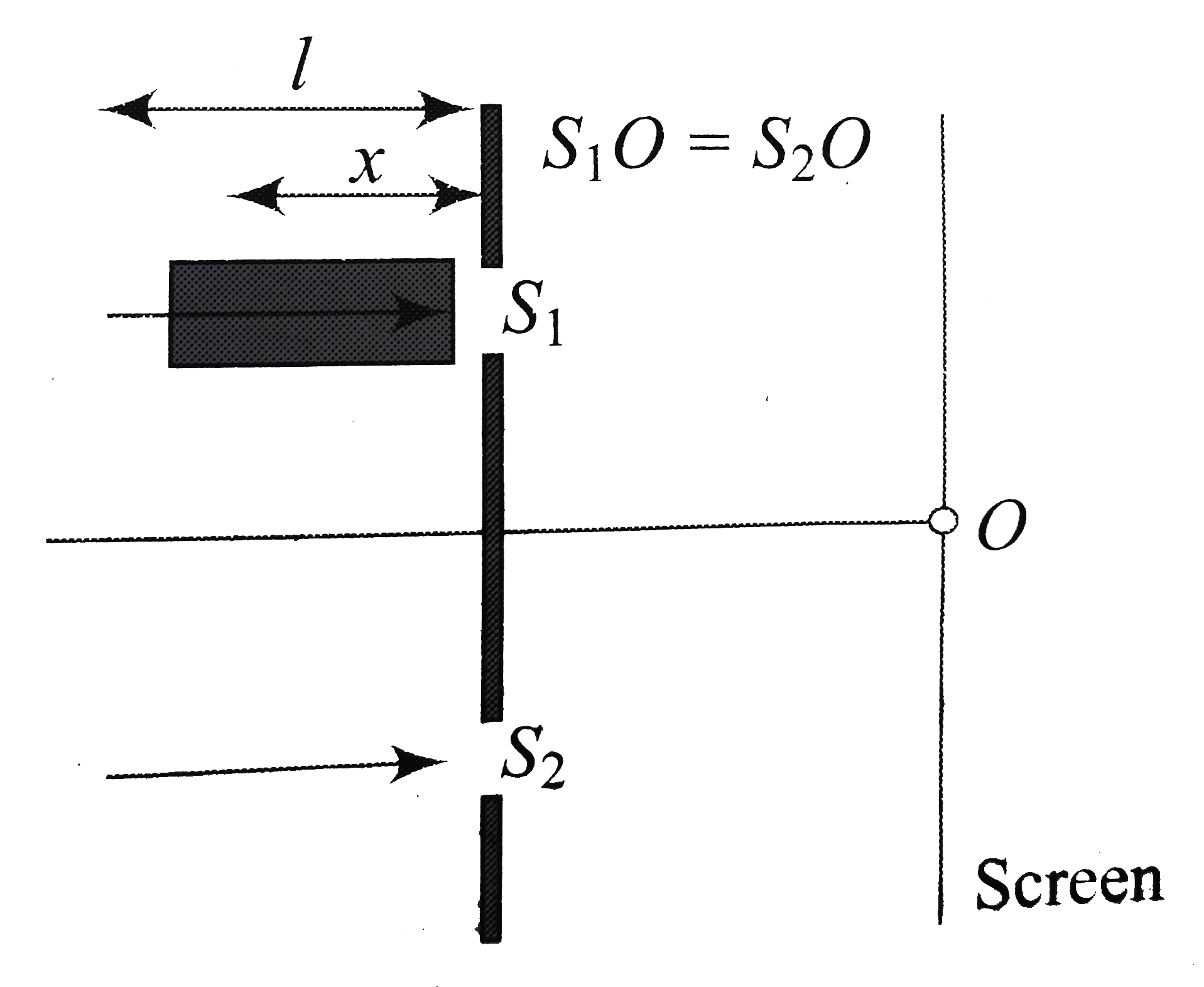
View SolutionIn figure, parallel beam of light is incident on the plane of the slits of a Young's double-slit experiment. Light incident on the slit `S_(1)` passes through a medium of variable refractive index `mu = 1 + ax` (where 'x' is the distance from the plane of slits as shown), up to distance 'I' before falling on `S_(1)`. Rest of the space is filled with air. If at 'O' a minima is formed. then the minimum value of the positive constant a (in terms of l and wavelength `lambda` in air) is
View SolutionTwo identical beam A and B of plane coherent waves of the sasme intensity and wavelength `lambda` fall on a plane screen. The direction of the beam propagations make angles `theta_(1)` and `theta_(2)` with the normal to the screen and lie in the same plane as shown in the figure. Find the distance `beta` between adject interfrence fringes on the screen.

View SolutionTwo identical beam A and B of wavelength `lambda` fall cylindeical screen. The angle between the directions a point P on the screen at angular position `phi` from the beam A as shown in the figure. Find the distance between adjacent interference fringes on the screen near the point P. Asume that the distance `beta` between adjacent fringes is much less than the radius of the cylinder.

View SolutionMonochromatic light waves of wavelength `lambda` from two coherent source fall on a larger plane screen. One of the waves is emanated from a point source S located at distance L from the screen and the other one is a broad plasne wave as shown in the figure. The spacing between the `n^(th)` and `(n-1)^(th)` bright fringe is

View SolutionA transparent slab of thickness t and refractive index `mu` is inserted in front of upper of YDSE apparauts. The wavelength of ligth used. is `lambda`. Assume that there is no absorption of light by the slab. Mark the correct statement(s).
View SolutionIn a YDSE with two identical slits, when the upper slit is covered with a thin, perfectly tranparent sheet of mica, the intensity at the centre of screen reduces ro `75%` of the initial value second minima is observed to the above this point and third maxima below it which of the following can not be a possible value of phase difference caused by the mica sheet
View SolutionIn Young's double slit experiment, the two slits are covered by slabs of same thickness but refractive index `1.4` and `1.7` . The distance between slits and screen is 1 m and distance between slits is 1mm and wavelength of coherent source used is `4000 overset(@)Delta` and the central fringe shifts to the 3rd bright fringe positions, then
View SolutionIn a Young's double slit experiment, the separation between the two slits is d and the wavelength of the light is `lamda`. The intensity of light falling on slit 1 is four times the intensity of light falling on slit 2. Choose the correct choice (s).
View SolutionA light source, which emits two wavelength `lamda_(1)=400nm` and `lamda_(2)=600nm`, is used in a Young's double slit experiment. If recorded fringe width for `lamda_(1)` and `lamda_(2)` are `beta_(1)` and `beta_(2)` and the number of fringes for them within a distance y on one side of the central maximum are `m_(1)` and `m_(2)` respectively, then
View SolutionWhile conduction the Young's double slit experiment, a student replaced the two slits with a large opaque plate in the x-y plane containing two small holes that act as two coherent point sources `(S_(1),S_(2))` emitting light of wavelength 600nm. The student mistakenly placed the screen parallel to the x-z plane `(for zgt0)` at a distance D=3 m from the mid-point of `S_(1)`,`S_(2)`, as shown schematically in the figure. The distance between the sources `d=0.6003 mm`. The origin O is at the intersection of the screen and the line joining `S_(1)S_(2)`. Which of the following is (are) true of the intensity pattern of the screen?
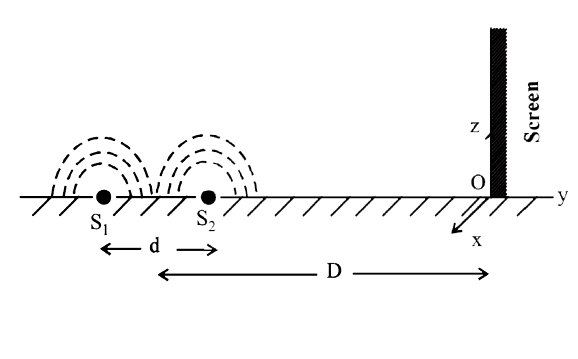
View SolutionIn YDSE, the sources is red ligth of wavelength `7 xx 10^(-7) m`. When a thin glass plate of refractive index 1.5 is put in the path of one of the interfering beams, the central bright fringe shifts by `10^(-3)` m to the position previously occupied by the 5th bright fringe.
What is the thickness of the plate?
View SolutionIn Young's experiment, the source is red light of wavelength `7xx10^(-7)m`. When a thin glass plate of refractive index `1.5` at this wavelength is put in the path of one of the intering beams, the central bright fringe shiffts by `10^(-3)m` to the position previously occupied by the `5^(th)` bright fringe.
When the source is now changed to green light of wavelength `5xx10^(-7)m`, the central fringe shifts to position initially occupied by the `6^(th)` bright fringe to red light. Find the refractive index of glass for green light.
View SolutionIn YDSE, the sources is red ligth of wavelength `7 xx 10^(-7) m`. When a thin glass plate of refractive index 1.5 is put in the path of one of the interfering beams, the central bright fringe shifts by `10^(-3)` m to the position previously occupied by the 5th bright fringe.
Change is fringe width produced due to chanbe in wavelength is
View SolutionIn YDSE arrangement as shown in figure, fringes are seen on screen using monochromatic source S having wavelength 3000 Å (in air). `S_1 `and `S_2` are two slits seperated by d = 1 mm and D = 1m. Left of slits `S_1` and `S_2` medium of refractive index `n_1 = 2` is present and to the right of `S_1` and `S_2` medium of `n_2 = 3/2`, is present. A thin slab of thickness 't' is placed in front of `S_1` . The refractive index of `n_3` of the slab varies with distance from it's starting face as shown in figure.

Fringe width on the screen is
View SolutionIn YDSE arangement shown in figure, fringes are seen on screen using monochromatic source S having wavelength `3000 overset(@)Delta` (in air). `S_(1)` and `S_(2)` are two slits separate by `d = 1mm` and `D = 1m` . Left of slits `S_(1) and S_(2)` medium of refractive index `mu_(1) = 2` is presernt refractive index `mu_(2) = (3)/(2)` is present. A thin slab of thickness 't' is placed in front of `S_(1)` . The refractive index of slab `mu_(3)` varies with distance from its starting face as shown in figure.

If the thickness of the slab is selected `1mu m` , then the position of the central maxima will be (y - coordinate)
View SolutionIn YDSE arrangement as shown in figure, fringes are seen on screen using monochromatic source S having wavelength 3000 Å (in air). `S_1 `and `S_2` are two slits seperated by d = 1 mm and D = 1m. Left of slits `S_1` and `S_2` medium of refractive index `n_1 = 2` is present and to the right of `S_1` and `S_2` medium of `n_2 = 3/2`, is present. A thin slab of thickness 't' is placed in front of `S_1` . The refractive index of `n_3` of the slab varies with distance from it's starting face as shown in figure.

Fringe width on the screen is
View SolutionIn fig., light of wavelength `lambda = 5000 Å` is incident on the slits (in a horizontally fixed place).
Here, `d = 1 mm` and `D = 1 m`
Take origin at O and XY plane as shown in the figure. The screen is released from rest from the initial position as shown
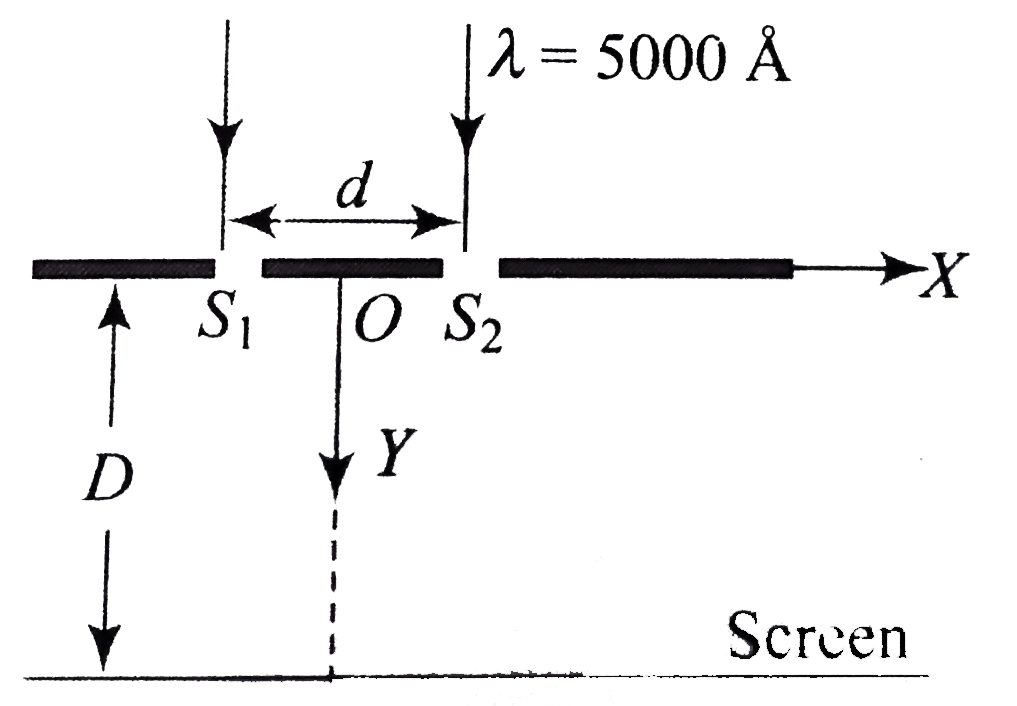
The velocity of central maxima at `t = 5 `s is
View SolutionIn fig., light of wavelength `lambda = 5000 Å` is incident on the slits (in a horizontally fixed place).
Here, `d = 1 mm` and `D = 1 m`
Take origin at O and XY plane as shown in the figure. The screen is released from rest from the initial position as shown
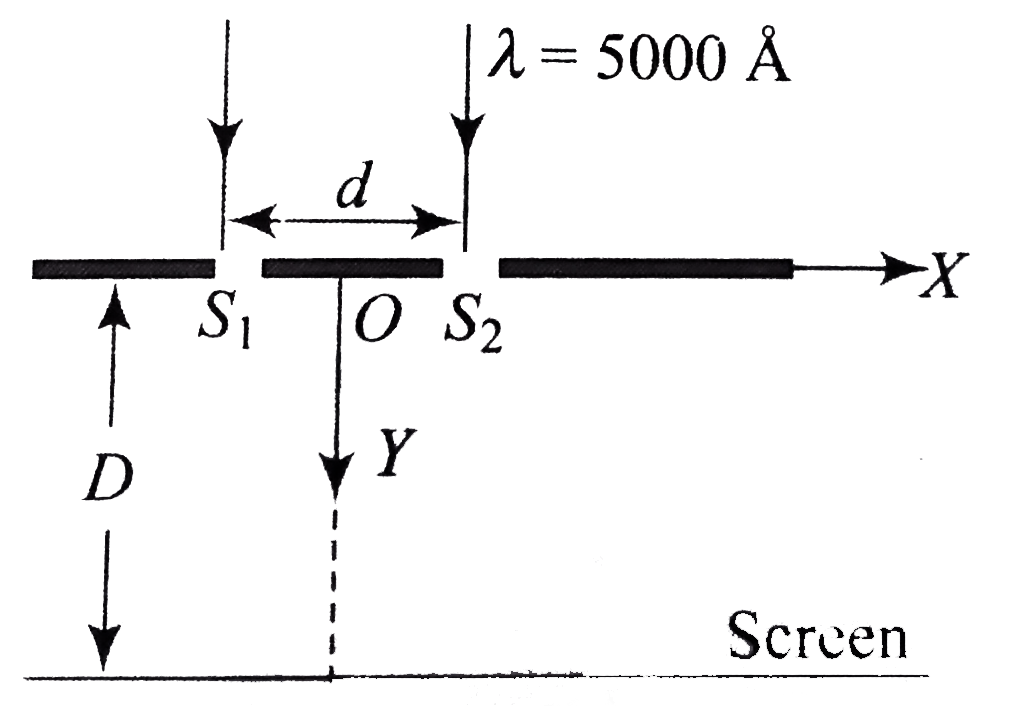
Velocity of 2nd maixma w.r.t central maxima at `t = 2`s is
View SolutionIn fig., light of wavelength `lambda = 5000 Å` is incident on the slits (in a horizontally fixed place).
Here, `d = 1 mm` and `D = 1 m`
Take origin at O and XY plane as shown in the figure. The screen is released from rest from the initial position as shown
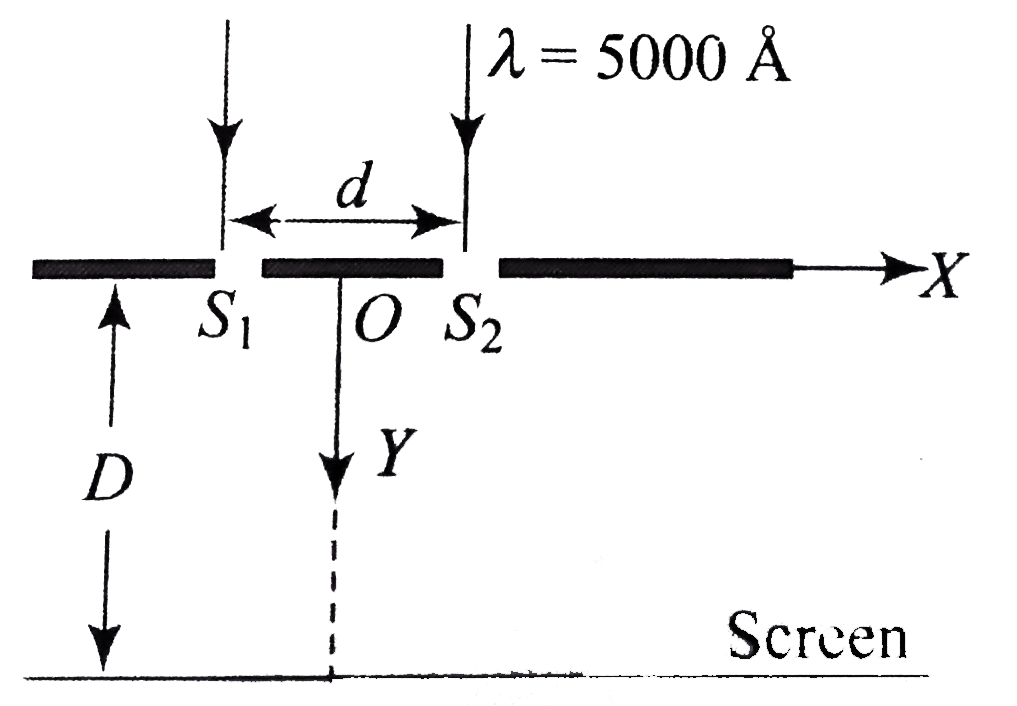
Acceleration of 3rd maxima w.r.t. 3rd maxima on other side of central maxima at `t = 3` s is
View SolutionA double slit apparatus is immersed in a liquid of refractive index 1.33. It has slit and the screen 1 mm. The slits are illuminated by a parallel beam of light whose wavelength in air is `6300 Å`
a. calculate the fringe width.
b. One of the slits of the apparatus is covered by a thin glass sheet of refractive index 1.53. Find the smallest thickness of the sheet to bring athe adjacent minima on the axis.
View SolutionA double slit apparatus is immersed in a liquid of refractive index 1.33. It has slit and the screen 1 mm. The slits are illuminated by a parallel beam of light whose wavelength in air is `6300 Å`
a. calculate the fringe width.
b. One of the slits of the apparatus is covered by a thin glass sheet of refractive index 1.53. Find the smallest thickness of the sheet to bring athe adjacent minima on the axis.
View SolutionA YDSE is performed in a medium of refractive index `4 // 3`, A light of 600 nm wavelength is falling on the slits having 0.45 nm separation . The lower slit `S_(2)` is covered b a thin glass plate of thickness 10.4 mm and refractive index 1.5. The interference pattern is observed on a screen placed 1.5 m from the slits as shown in figure. (All the wavelengths in this problem are for the given medium of refractive index `4 // 3`, ignore absorption.)
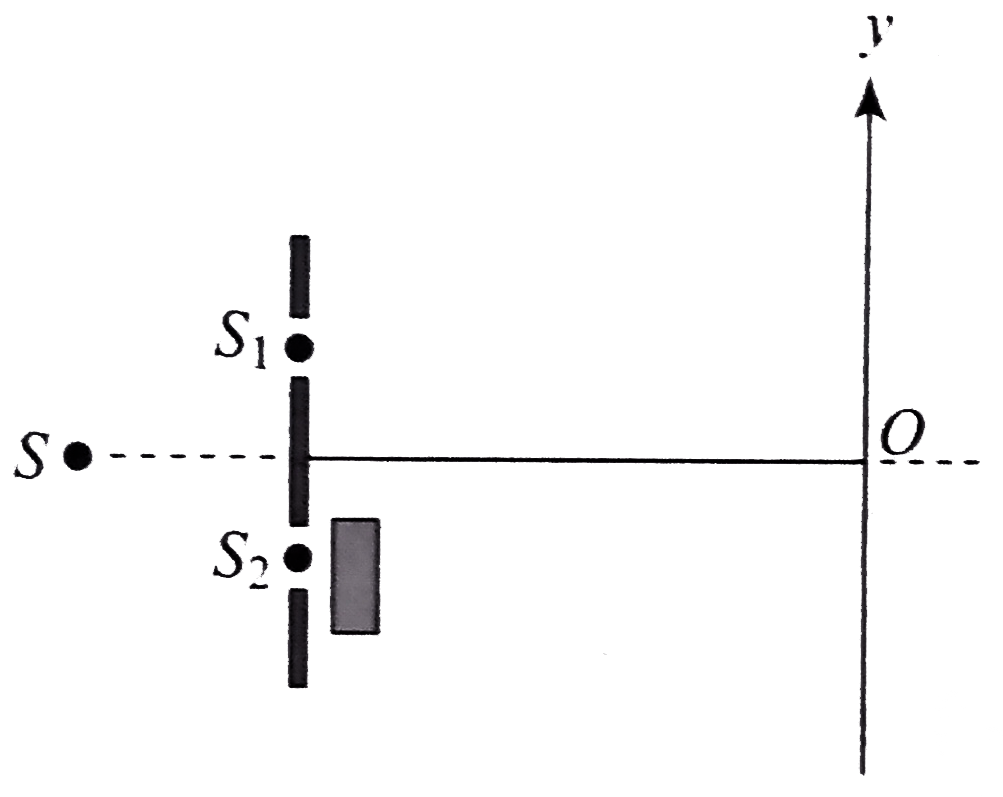
The location of the central maximum (bright fringe with zero path difference) on the y-axis will be
View SolutionA YDSE is performed in a medium of refractive index `4 // 3`, A light of 600 nm wavelength is falling on the slits having 0.45 nm separation . The lower slit `S_(2)` is covered b a thin glass plate of thickness 10.4 mm and refractive index 1.5. The interference pattern is observed on a screen placed 1.5 m from the slits as shown in figure. (All the wavelengths in this problem are for the given medium of refractive index `4 // 3`, ignore absorption.)

Find the light intensity at point O relative t maximum fringe intensity.
View SolutionA YDSE is performed in a medium of refractive index `4 // 3`, A light of 600 nm wavelength is falling on the slits having 0.45 nm separation . The lower slit `S_(2)` is covered b a thin glass plate of thickness 10.4 mm and refractive index 1.5. The interference pattern is observed on a screen placed 1.5 m from the slits as shown in figure. (All the wavelengths in this problem are for the given medium of refractive index `4 // 3`, ignore absorption.)

Now, if 600 nm, find the wavelength of the ligth that forms maximum exactly at point O.
View SolutionThe arrangement for a mirror experiment is shown in figure. S is a point source of frequency `6xx10^(14)Hz`. D and C represent the two ends of a mirror placed horizontally and LOM represents the screen.

Determine the width of the region where the fringes will be visible
View SolutionThe arrangement for a mirror experiment is shown in figure. S is a point source of frequency `6xx10^(14)Hz`. D and C represent the two ends of a mirror placed horizontally and LOM represents the screen.

Find the fringe width of the fringe pattern ?
View SolutionThe arrangement for a mirror experiment is shown in figure. S is a point source of frequency `6xx10^(14)Hz`. D and C represent the two ends of a mirror placed horizontally and LOM represents the screen.

Calculate the number of fringes
View SolutionIn YDSE, the intensity of light at a point on the screen is I for a path difference `lambda` . The intensity of light at a point where the path difference becomes `(lambda)/(3)` is `(I)/(P)` . Find the value of P ?
View SolutionIn YDSE, the slits separation is `0.6mm` and the separation between slit and screen is `1.2m`. The wavelength of light used is `4800 overset(@)AA` . The angular fringe width is `Pxx10^(-4)` radian. Find the value of P ?
View SolutionIn YDSE, the slits have different widths. As a result, amplitude of waves from slits are A and 2A respectively. If `I_(0)` be the maximum intensity of the intensity of the interference pattern then the intensity of the pattern at a point where the phase difference between waves is `phi` is given by `(I_(0))/(P)(5+4cos phi)` . Where P is in in integer. Find the value of P ?
View SolutionA Young's double slit interference arrangement with slits `S_(1)` and `S_(2)` is immersed in water (refractive index `=4//3`) as shown in the figure. The positions of maxima on the surface of water are given by `x^(2) = p^(2)m^(2)lambda^(2)-d^(2)`, where `lambda` is the wavelength of light in air (reflactive index = 1), 2d is the separation between the slits and m is an integer. The value of P is ..........

View Solution
LEVEL - VI questions and complete solutions for chapter WAVE OPTICS of NARAYANA PHYSICS (HINGLISH) of Class 12
All Exercises from NARAYANA Class 12 PHYSICS WAVE OPTICS
- C . U . Q (Diffraction light)
- C . U . Q (interference)
- C . U . Q (Polarisation)
- C . U . Q (Resolving power)
- C.U.Q
- Evaluate yourself - 1
- Evaluate yourself - 2
- Evaluate yourself - 3
- Example
- Exercise - 1 (C.W) Huygen. s principle
- Exercise - 1 (C.W) Interference
- Exercise - 1 (C.W) Diffraction
- Exercise - 1 (C.W) Resolving power
- Exercise - 1 (C.W) Polarisation
- Exercise - 1 (C.W) Diffraction
- Exercise - 1 (H.W) Diffraction
- Exercise - 1 (H.W) Interference
- Exercise - 1 (H.W) Polarisation
- Exercise - 1 (H.W) Resolving power
- Exercise - 2 (C . W) Diffraction
- Exercise - 2 (C . W) Polarisation
- Exercise - 2 (C . W) Resolving power
- Exercise - 2 (C . W) Interference
- Exercise - 2 (H. W) Diffraction
- Exercise - 2 (H. W) Interference
- Exercise - 2 (H. W) Polarisation
- Exercise - 3
- Exercise - 4 Diffraction
- Exercise - 4 Interference of light
- Exercise - 4 Polarisation
- Exercise -1 (C.W) Diffraction
- Exercise -1 (C.W) Resolving power
- Exercise -1 (C.W) Huygen. s principle
- Exercise -1 (C.W) Huygen. s principle
- LEVEL - I (C.W)
- LEVEL - I(H.W)
- LEVEL - II (C.W)
- LEVEL - II(H.W)
- LEVEL - III
- LEVEL - V
- LEVEL - VI
- NCERT Based Questions