एक गोलीय सममित आवेश वितरण दिया गया है जसमे आवेश घनत्व इस प्रकार परिवर्तित होता है-
ρ(r)=ρ0(54−rR),r=R तक तथा ρ(r)=0,r>R के लिए, जहां r मूलबिंदु से दुरी है। मिलबिंदु से दुरी r(r<R) पर विधुत क्षेत्र इस प्रकार दिया जाता है -
4πρ0r3ε0(53−rR)
ρ0r4ε0(53−rR)
4ρ0r3ε0(54−rR)
ρ0r3ε0(54−rR)
The correct Answer is:B
x त्रिज्या और dx मोटाई के एक गोलीय कोश कि कल्पना करो।
तब dq=ρ(x)4πx2dx=ρ0(54−xR).4πx2dx
∴q=4πρ0∫r0(54−xR)x2dx=4ρ0(5r312−r24R)
अतः E=14πε0.qr2=ρ0r4ε0(53−rR).
Topper's Solved these Questions
- वैधुत आवेश और क्षेत्र BOOK - NAVBODHCHAPTER - वैधुत आवेश और क्षेत्र EXERCISE - NCERT पाठ्यपुस्तक के प्रश्नोत्तर
53 Videos
- वैधुत आवेश और क्षेत्र BOOK - NAVBODHCHAPTER - वैधुत आवेश और क्षेत्र EXERCISE - बोधात्मक प्रश्न प्लस
19 Videos
- वैद्युत आवेश तथा क्षेत्रBOOK - NAVBODHCHAPTER - वैद्युत आवेश तथा क्षेत्रEXERCISE - तथ्यात्मक प्रश्न
12 Videos
- संचार व्यवस्था BOOK - NAVBODHCHAPTER - संचार व्यवस्था EXERCISE - NCERT पाठ्य पुस्तक के प्रश्नोत्तर
9 Videos
Similar Questions
वायु में एक-दूसरे से 30 cm दुरी पर रखे दो छोटे आवेशित गोलों पर क्रमशः 2×10−7 तथा 3×10−7 आवेश है। उनके बीच कितना बल है ?
View Solutionतीन आवेश +2q−q और +3q प्रदर्शित किए गए है। दो आवेश +2q और −q एक बंद पृष्ठ S के अंदर है। इस अभी विन्यास के कारण पृष्ठ S से गुजरने वला वैधुत फ्लक्स कितना होगा ?
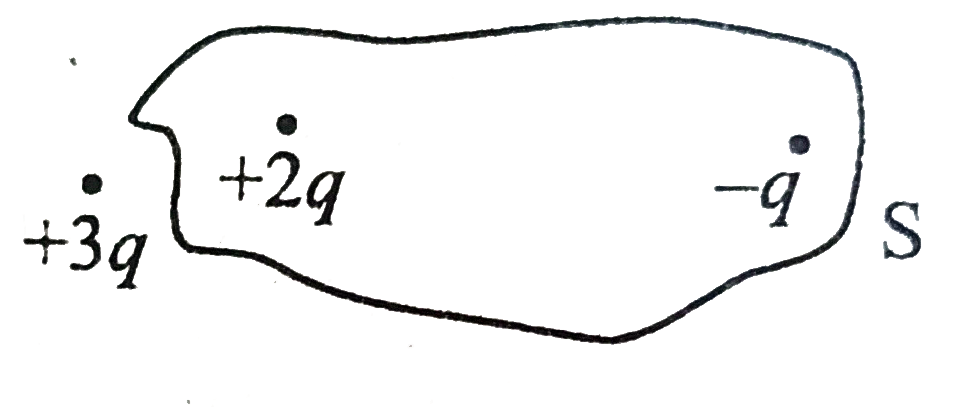
View Solutionसामान्य विधूतरोधी होता है , किन्तु वायुयान के रबर टायर कुछ चालक बनाये जाते है , क्यों ?
View Solutionव्योम तरंगो के उपयोग द्वारा क्षितिज के पार संचार के लिए निम्नलिखित अवृत्तयियो में से कोण -सी आवृतिया उपयुक्त रहेगी -
View SolutionLet there be a spherically symmetric charge distribution with charge density varying as rho(r)=rho(5/4-r/R) upto r=R , and rho(r)=0 for rgtR , where r is the distance from the origin. The electric field at a distance r(rltR) from the origin is given by
View SolutionA non-homogenous sphere of radius R has the following density variation.
ρ=ρ0,r≤r/3,
ρ=ρ0/2,R3<r≤3R4,
ρ=ρ08,(3R)/(4)<r≤R,
What is the gravitational field due to sphere at distance 2R from center?
View SolutionA solid ball of radius R has a charge density rho given by rho = rho_(0)(1-(r )/(R )) for 0le r le R The electric field outside the ball is :
View Solution[" Consider a spherical symmetric "],[" charge distribution with charge "],[" density varying as "],[[rho={[rho_(0)(1-(r)/(R)),r R]]
View Solutionयदि संक्रिया ∗ वास्तविक संख्याओं के समुच्चय R पर द्विआधारी संक्रिया है तथा इस प्रकार परिभाषित है कि
a∗b=√a4+b4 , जहाँ a,b∈R से दिखाइए कि '∗' क्रम-विनिमेय नियम का पालन करती है।
View Solutionयदि f:R→R इस प्रकार है कि f(x) = |x|, तो सिद्ध कीजिए कि fof = f .
View SolutionLet there be a spherical symmetric charge density varying as p(r)=p0rR upto r = R and ρ(r)=0 for r>R, where r is the distance from the origin. The electric field at on a distance r(r<R) from the origin is given by -
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionयदि R त्रिज्या का एक वृत्त मूलबिंदु O से होकर जाता है तथा निर्देशांक अक्षो को A और B पर कट्टा है , तो O से रेखा AB पर डाले गए लम्ब के पाद का बिन्दुपथ है
View Solutionदिया है की समीकरण z2+(p+iq)z+r+is=0 जहाँ p,q,r शून्येतर है के मूल वास्तविक है तब
View SolutionLet there be a spherically symmetric charge distribution with charge density varying as rho(r)=rho(5/4-r/R) upto r=R , and rho(r)=0 for rgtR , where r is the distance from the origin. The electric field at a distance r(rltR) from the origin is given by
View SolutionLet there be a spherically symmetric charge distribution with charge density varying as ρ(r)=ρ0(54−rR) upto r = R, and ρ(r)=0 for r >R, where r is the distance from the origin. The electric field at a distance r (r
View Solution
