Complete Solutions to प्रश्नावली (दीर्घ उत्तरीय प्रश्न (L.A.)) of chapter प्रायिकता of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | प्रायिकता |
| NCERT EXEMPLAR HINDI | प्रश्नावली (दीर्घ उत्तरीय प्रश्न (L.A.)) |
| Number Of Questions | 24 |
| Academic Year | 2023-24 |
तीन थैलों में लाल तथा सफेद गेंदों की संख्या निम्नलिखित है :
थैला प्रथम - 3 लाल गेंद
थैला द्वितीय - 2 लाल गेंद तथा 1 सफेद गेंद
थैला तृतीय - 3 सफेद गेंद
थैला i के चुने जाने तथा उसमें से एक गेंद के चयन की प्रायिकता `(i)/(6)` है, i = 1, 2, 3। इस बात की प्रायिकता क्या है कि :
(i) एक लाल गेंद चुनी जाती है? (ii) एक सफेद गेंद चुनी जाती है?
View Solutionतीन थैलों में लाल तथा सफेद गेंदों की संख्या निम्नलिखित है :
थैला प्रथम - 3 लाल गेंद
थैला द्वितीय - 2 लाल गेंद तथा 1 सफेद गेंद
थैला तृतीय - 3 सफेद गेंद
थैला i के चुने जाने तथा उसमें से एक गेंद के चयन की प्रायिकता `(i)/(6)` है, i = 1, 2, 3। इस बात की प्रायिकता क्या है कि :
(i) एक लाल गेंद चुनी जाती है? (ii) एक सफेद गेंद चुनी जाती है?
View Solutionतीन थैलों में लाल तथा सफेद गेंदों की संख्या निम्नलिखित है :
थैला प्रथम - 3 लाल गेंद
थैला द्वितीय - 2 लाल गेंद तथा 1 सफेद गेंद
थैला तृतीय - 3 सफेद गेंद
यदि एक सफेद गेंद चुनी जाती है, तो इस बात की क्या प्रायिकता है कि यह गेंद :
(i) थैला 2
(ii) थैला 3 से निकाली गयी है?
View Solutionतीन थैलों में लाल तथा सफेद गेंदों की संख्या निम्नलिखित है :
थैला प्रथम - 3 लाल गेंद
थैला द्वितीय - 2 लाल गेंद तथा 1 सफेद गेंद
थैला तृतीय - 3 सफेद गेंद
यदि एक सफेद गेंद चुनी जाती है, तो इस बात की क्या प्रायिकता है कि यह गेंद :
(i) थैला 2
(ii) थैला 3 से निकाली गयी है?
View Solutionएक दुकानदार तीन प्रकार के फूलों के बीज `A_(1), A_(2)` तथा `A_(3)` बेचता है। बीजों को 4:4:2 के अनुपात में मिलाकर बेचा जाता है । इन तीन प्रकार के बीजों के अंकुरण की दर क्रमश: 45%, 60% तथा 35% है। निम्नलिखित प्रायिकताओं का परिकलन कीजिए:
एक यादृच्छया चुने गए बीज के अंकुरित होने की
View Solutionएक दुकानदार तीन प्रकार के फूलों के बीज `A_(1), A_(2)` तथा `A_(3)` बेचता है। बीजों को 4:4:2 के अनुपात में मिलाकर बेचा जाता है । इन तीन प्रकार के बीजों के अंकुरण की दर क्रमश: 45%, 60% तथा 35% है। निम्नलिखित प्रायिकताओं का परिकलन कीजिए:
बीज के अंकुरित नहीं होने की, दिया हुआ है कि बीज का प्रकार `A_(3)` है।
View Solutionएक दुकानदार तीन प्रकार के फूलों के बीज `A_(1), A_(2)` तथा `A_(3)` बेचता है। बीजों को 4:4:2 के अनुपात में मिलाकर बेचा जाता है । इन तीन प्रकार के बीजों के अंकुरण की दर क्रमश: 45%, 60% तथा 35% है। निम्नलिखित प्रायिकताओं का परिकलन कीजिए:
बीज का प्रकार `A_(2)` होने की, दिया हुआ है कि यादृच्छया चुना गया बीज अंकुरित नहीं होता है।
View Solutionयह ज्ञात है कि एक पत्र या तो TATA NAGAR से या CALCUTTA से आया है। पत्र के लिफाफे पर केवल दो क्रमागत अक्षर TA दिखलाई पड़ते हैं। पत्र के TATA NAGAR से आने की प्रायिकता क्या है?
View Solutionप्रथम थैले मैं `3` काले और `4` सफेद गेंदें है जबकि द्वितीय थैले मैं `4` काली और `3` सफेद गेंदें हैं। एक अनभिनत पासे को उछला जाता है। यदि पासे पर `1` या `3` का अंक प्रकट होता है तब प्रथम थैले मैं से एक गेंद निकली जाती है तथा यदि अन्य अंक प्रकट होता है तब द्वितीय थैले मे से एक गेंद निकली जाती है। निकली गयी गेंद के काली होने की प्रायिकता ज्ञात कीजिये।
View Solutionतीन कलशों में क्रमश: 2 सफेद तथा 3 काली गेंद, 3 सफेद तथा 2 काली गेंद और 4 सफेद तथा 1 काली गेंद हैं। प्रत्येक कलश के चुने जाने की प्रायिकता समान है। चुने गए कलश से एक गेंद यदृच्छया निकाली जाती है और वह सफेद रंग की पाई जाती है। इस बात की प्रायिकता ज्ञात कीजिए वह गेंद दूसरे कलश से निकाली गई है।
View Solutionछाती के एक्स-रे की जाँच द्वारा क्षय रोग (T.B.) के पहचान की प्रायिकता 0.99 है, जबकि व्यक्ति वास्तव में क्षय रोग से ग्रसित है। एक स्वस्थ व्यक्ति के क्षय रोग से ग्रसित पाये जाने की प्रायिकता 0.001 है। किसी शहर में 1,000 लोगों में से 1 में क्षय रोग पाया जाता है। एक व्यक्ति यदृच्छया चुना जाता है और निदान किए जान पर पता चलता है कि उसे क्षय रोग हो इस बात की प्रायिकता क्या है कि उसे वास्तव में क्षय रोग है।
View Solutionकोई वस्तु A, B तथा C तीन मशीनों द्वारा निर्मित होती है। किसी विशिष्ट अवधि में निर्मित वस्तुओं की कुल संख्या में से 50% A पर, 30% B पर तथा 20% C पर निर्मित होती है। A पर उत्पादित वस्तुओ का 2% तथा B पर उत्पादित वस्तुओं का 2% खराब है और उन वस्तुओं का 3% जो C पर उत्पादित होती हैं, खराब है। सभी वस्तुओं को एक गोदाम में रखते हैं। एक वस्तु को यदृच्छया निकाला जाता है और वह खराब पायी जाती है। इस बात की प्रायिकता क्या है कि वह वस्तु मशीन A पर निर्मित हुई है?
View Solutionमान लीजिए कि X एक असंतत यादृच्छिक चर है, जिसका प्रायिकता बंटन निम्नलिखित प्रकार से परिभाषित है।
`P(X=x)= {[K(x+1),x = "1,2,3,4 "`के लिए`], [2kx , x= "5,6,7 "`के लिए`"]`, `[0, "`अन्य स्थिति में`]}
k का मान
View Solutionमान लीजिए कि X एक असंतत यादृच्छिक चर है, जिसका प्रायिकता बंटन निम्नलिखित प्रकार से परिभाषित है।
`P(X=x)= {[K(x+1),x = "1,2,3,4 "`के लिए`], [2kx , x= "5,6,7 "`के लिए`"]`, `[0, "`अन्य स्थिति में`]}
k का मान
View Solutionमान लीजिए कि X एक असंतत यादृच्छिक चर है, जिसका प्रायिकता बंटन निम्नलिखित प्रकार से परिभाषित है।
`P(X=x)= {[K(x+1),x = "1,2,3,4 "`के लिए`], [2kx , x= "5,6,7 "`के लिए`"]`, `[0, "`अन्य स्थिति में`]}
k का मान
View Solutionकिसी असंतत यादृच्छिक चर X का प्रायिकता बंटन निम्नलिखित है।
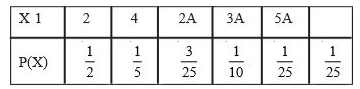
निम्नलिखित को परिकलित कीजिए ।
A का मान, यदि E(X) = 2.94
View Solutionकिसी असंतत यादृच्छिक चर X का प्रायिकता बंटन निम्नलिखित है।

निम्नलिखित को परिकलित कीजिए ।
A का मान, यदि E(X) = 2.94
View Solutionकिसी यादृच्छिक चर x का प्रायिकता-बंटन नीचे दिया है ।
`P(X=x)= {[Kx^(2),x = "1,2,3,4 के, लिए"], [2kx , x= "5,6,7 के, लिए"], [0, "अन्यथा, अन्य, स्थिति, में"]}`
जहाँ k एक अचर है। परिकलित कीजिए।
`P(X ge 4)`
View Solutionकिसी यादृच्छिक चर x का प्रायिकता-बंटन नीचे दिया है ।
`P(X=x)= {[Kx^(2),x = "1,2,3,4 के, लिए"], [2kx , x= "5,6,7 के, लिए"], [0, "अन्यथा, अन्य, स्थिति, में"]}`
जहाँ k एक अचर है। परिकलित कीजिए।
`E(3X^(2))`
View Solutionकिसी यादृच्छिक चर x का प्रायिकता-बंटन नीचे दिया है ।
`P(X=x)= {[Kx^(2),x = "1,2,3,4 के, लिए"], [2kx , x= "5,6,7 के, लिए"], [0, "अन्यथा, अन्य, स्थिति, में"]}`
जहाँ k एक अचर है। परिकलित कीजिए।
`P(X ge 4)`
View Solutionएक थैले में (2n + 1) सिक्के हैं। यह ज्ञात है कि इनमें से n सिक्के अनभिनत (न्याय्य) हैं। थैले से एक सिक्का यदृच्छया निकाला जाता है और उसे उछाला जाता है। यदि उछालने पर 'चित' प्राप्त होने की प्रायिकता `(31)/(42)` है तो n का मान निर्धारित कीजिए।
View Solutionताश की एक भली-भाँति फेंटी हुई गड्डी से दो पत्ते उत्तरोत्तर बिना प्रतिस्थापन के निकाले जाते हैं। यादृच्छिक चर X का माध्य तथा मानक प्रसरण ज्ञात कीजिए, जँहा X इक्कों की संख्या हैं ।
View Solutionएक पासा दो बार उछाला जाता है। एक विषम संख्या प्राप्त करना सफलता है। सफलताओं की संख्याओं का प्रसरण ज्ञात कीजिए।
View Solution5 पत्ते 1 से 5, तक संख्यांकित हैं । एक पत्ते पर एक ही संख्या अंकित हैं । दो पत्ते यादृच्छया बिना प्रतिस्थापन के निकाले जाते हैं । मान लीजिए कि निकाले गए दो पत्तों पर अंकित संख्याओं का योगफल X से निरुपित होता है। X का माध्य तथा प्रसरण ज्ञात कीजिए।
View Solution
प्रश्नावली (दीर्घ उत्तरीय प्रश्न (L.A.)) questions and complete solutions for chapter प्रायिकता of NCERT EXEMPLAR HINDI of Class 12