Complete Solutions to प्रश्नावली (वस्तुनिष्ठ प्रश्न) of chapter प्रायिकता of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | प्रायिकता |
| NCERT EXEMPLAR HINDI | प्रश्नावली (वस्तुनिष्ठ प्रश्न) |
| Number Of Questions | 38 |
| Academic Year | 2023-24 |
यदि `P(A)= (4)/(5)` तथा `P(Ann B) = (7)/(10)` तो P(B | A) का मान
View Solutionयदि `P(AnnB)= (7)/(10)` तथा `P( B) = (17)/(20)` तो P(A | B) बराबर है।
View Solutionयदि `p(A) = (3)/(10), P(B) = (2)/(5)` तथा `P(A uu B) = (3)/(5),` तो `P(B//A) + P(A//B)` के बराबर है :
View Solutionयदि `P(A)= (2)/(5), P(B)= (3)/(5)` तथा `P(AnnB)= (1)/(5)` तो `P(A|B).P(B'|A') बराबर है
View Solutionयदि A तथा B दो घटनाएँ ऐसी हैं कि `P(A) = (1)/(2), P(B) = (1)/(3), P(A//B)= (1)/(4)` तो `P(A'nnB')` बराबर है।
View Solutionयदि P(A) = 0.4, P(B) = 0.8 तथा P(B | A) = 0.6, तो `P(Auu B)` बराबर है।
View Solutionयदि A तथा B दो घटनाएँ हैं और, `A ne phi, B ne phi` तो
View SolutionA तथा B घटनाएँ इस प्रकार हैं कि P(A) = 0.4, P(B) = 0.3 और `P(A uu B) = 0.5` P (B A) बराबर है।
View Solutionआपको ऐसी दो घटनाएँ A तथा B दी हुई हैं कि `P(B)= (3)/(5), P(A| B) = (1)/(2)` और `P(AuuB)= (4)/(5)` तो P(A) बराबर है।
View Solutionआपको ऐसी दो घटनाएँ A तथा B दी हुई हैं कि `P(B)=(3)/(5) P(A//B)=(1)/(2)` और `P(AuuB)=(4)/(5)` तो P(B/A) बराबर है।
View Solutionयदि `P(B) = (3)/(5), P(A|B)= (1)/(2)` तथा `P(A uuB) = (4)/(5)` , तो `P(A uuB) + P(Auu B)` बराबर है।
View Solutionमान लीजिए कि `P(A) = (7)/( 13 ),P(B)= (9)/(13)` तथा `P(Ann B) = (4)/( 13)` तो P( A | B) बराबर है।
View Solutionयदि A तथा B ऐसी घटनाएँ हैं कि `P(A) gt 0` और `P(B) ne 1`, तो P( A' | B' ) बराबर है:
View Solutionयदि A तथा B दो स्वतंत्र घटनाएँ हैं और `P(A)= (3)/(5)` तथा `P(B) = (4)/(9)` , तो `P(A nnB )` बराबर है:
View Solutionयदि दो घटनाएँ स्वंतत्र हैं, तो
View Solutionमान लीजिए कि A तथा B दो घटनाएँ इस प्रकार हैं कि `P(A) = (3)/(8), P(B)= (5)/(8)` तथा `P(Auu B) = (3)/(4)` तो `P(A | B).P( A| B) ` बराबर है:
View Solutionयदि घटनाएँ A तथा B स्वंतत्र हैं, तो `P(AnnB)` बराबर है
View Solutionदो घटनाएँ E तथा F स्वतंत्र हैं। यदि P(E) = 0.3, `P(E uu F ) = 0.5`, तो `P(E|F)-P(F|E)` बराबर है
View Solutionएक थैले में 5 लाल तथा 3 नीली गेंद हैं। यदि 3 गेंद यादृच्छया बिना प्रतिस्थापन के निकाली जाती हैं, तो तथ्यत: एक लाल रंग की गेंद के निकालने की प्रायिकता
View Solutionएक थैले में 5 लाल तथा 3 नीली गेंद हैं। तीन गेंदों में से तथ्यतः दो गेंदों के लाल रंग की प्रायिकता, जबकि पहली गेंद लाल रंग की है -
View Solutionतीन व्यक्ति A, B तथा C, A से प्रारम्भ करके, एक लक्ष्य पर बारी बारी से गोली चलाते हैं। उनके द्वारा लक्ष्य-भेदन की प्रायिकताएँ क्रमश: 0.4,0.3 तथा 0.2 हैं। दो बार लक्ष्य - भेदन की प्रायिकता है-
View Solutionमान लीजिए कि पैदा होने वाले प्रत्येक बच्चे का लड़का या लड़की होना सम संभाव्य है। तथ्यत: (exactly) तीन बच्चों वाले एक परिवार पर विचार कीजिए।
(a) उस प्रतिदर्श समष्टि के आठ अवयवों की सूची बनाइए, जिसके परिणामों में तीनों बच्चों के लड़का या लड़की होने की सभी संभावनाएँ निहित हों।
(b) नीचे लिखी प्रत्येक घटना को समुच्चय रूप में लिखिए और उसकी प्रायिकता ज्ञात कीजिए:
(i) घटना कि तत्थ्यत: एक बच्चा लड़की है।
ii) घटना कि कम से कम दो बच्चे लड़की है।
(iii) घटना की एक भी बच्चा लड़की नहीं है।
View Solutionएक पासा फेंका जाता है। पासे पर सम संख्या के प्राप्त होने की प्रायिकता है
View Solutionकिसी बॉक्स में 3 नारंगी, 3 हरी तथा 2 नीली गेंद हैं। बॉक्स से तीन गेंद यादृच्छया बिना प्रतिस्थापन के निकाली जाती हैं, तो दो हरी गेंद तथा एक नीली गेंद के निकालने की प्रायिकता है
View Solutionएक फ्लैश लाइट (कौंध बत्ती) में 8 बैटरी हैं जिनमें से तीन निस्तेज (dead) है। यदि दो बैट्रियों को बिना प्रतिस्थापन के चुनकर जाँचा जाता है तो उन दोनों के निस्तेज होने की प्रायिकता है
View Solutionआठ सिक्कों को एक साथ उछाला जाता है । ठीक 3 चित प्राप्त होने की प्रायिकता है
View Solutionदो पासे फेंके जाते हैं। यदि यह ज्ञात है कि पासों पर प्राप्त संख्याओं का योगफल 6 से कम था तो उन पर प्राप्त संख्याओं का योग 3 होने की प्रायिकता है
View Solutionनिम्नलिखित में से कौन सा कथन द्विपद-बंटन के लिए आवश्यक नहीं है
View Solutionताश के 52 पत्तों की भली-भाँति फेंटी हुई किसी गड्डी से दो पत्ते प्रतिस्थापन सहित निकाले जाते हैं। दोनों पत्तों के 'रानी' होने की प्रायिकता है,
View Solutionसत्य" तथा "असत्य" के टेस्ट में 10 में से कम से कम 7 सही उत्तर के अनुमान लगाने की प्रायिकता =
View Solutionकिसी व्यक्ति के तैराक नहीं होने की प्रायिकता 0.3 है। 5 व्यक्तियों में से 4 के तैराक होने की प्रायिकता है :
View Solutionकिसी असंतत यादृच्छिक चर X का प्रायिकता- बंटन नीचे दिया हुआ है:
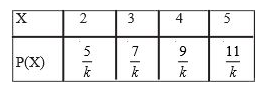
k का मान है,
View Solutionनिम्नलिखित प्रायिकता बंटन के लिए E (X)का मान है,

View Solutionनिम्नलिखित प्रायिकता- बंटन के लिए `E(X^(2))` का मान
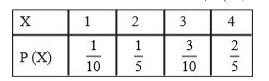
View Solutionमान लीजिए कि एक यादृच्छिक चर X, प्राचल n तथा p वाले द्विपद-बंटन का पालन करता है, जहाँ `0lt p lt 1` यदि `P(x=r)//P(x=n-r),n` तथा r से स्वतंत्र है, तो p बराबर है
View Solutionकिसी महाविद्यालय में, 30% विद्यार्थी भौतिक विज्ञान में अनुत्तीर्ण होते हैं, 25% गणित में अनुत्तीर्ण होते हैं तथा 10% दोनों विषयों में अनुत्तीर्ण होते हैं। एक विद्यार्थी यादृच्छया चुना जाता है। इस बात की प्रायिकता कि वह भौतिक विज्ञान में अनुत्तीर्ण है यदि वह गणित में अनुत्तीर्ण हो चुका है।
View SolutionA तथा B दो विद्यार्थी हैं। उनके द्वारा किसी प्रश्न को सही प्रकार से हल करने की संभावनाएँ क्रमशः `(1)/(3)` तथा `(1)/(4)` हैं। यदि उनके द्वारा एक ही प्रकार की गलती करने की प्रायिकता `(1)/(20)` हैं तथा उनके उत्तर समान हैं, तो उनके द्वारा प्राप्त उत्तर के सही होने की प्रायिकता है,
View Solutionएक बॉक्स में 100 कलम हैं, जिसमें से 10 कलम खराब हैं। इस बात की प्रायिकता क्या है कि बिना प्रतिस्थापित किए एक-एक करके निकाले गए 5 कलमों के किसी नमूने में अधिक से अधिक 1 कलम खराब है,
View Solution
प्रश्नावली (वस्तुनिष्ठ प्रश्न) questions and complete solutions for chapter प्रायिकता of NCERT EXEMPLAR HINDI of Class 12