Complete Solutions to प्रश्नावली (लघु उत्तरीय प्रश्न (S.A.)) of chapter प्रायिकता of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | प्रायिकता |
| NCERT EXEMPLAR HINDI | प्रश्नावली (लघु उत्तरीय प्रश्न (S.A.)) |
| Number Of Questions | 53 |
| Academic Year | 2023-24 |
किसी भारित पासे के लिए घटित होने वाले परिणामो की प्रायिकताएँ नीचे दी हुई है : `P(1) = P(2) = 0.2, (3) = P(5) = P(6) = 0.1` तथा `P(4) = 0.3`
पासे को दो बार फेका जाता है | मान लीजिए कि A तथा B क्रमशः घटनाओं प्रत्येक बार एक ही संख्या आना तथा B घटना कुल स्कोर 10 या 10 से अधिक आना को निरूपित करता है | निर्धारित कीजिए कि A तथा B स्वतंत्र घटनाएं है या नहीं
View Solution। यदि पासा अनभिनत हो, तो निर्धारित कीजिए कि घटनाएँ A तथा B स्वतंत्र होंगी या नहीं।
`bb"प्रश्न संख्या 1"`
किसी भारित पासे के लिए घटित होने वाले परिणामो की प्रायिकताएँ नीचे दी हुई है : `P(1) = P(2) = 0.2, (3) = P(5) = P(6) = 0.1` तथा `P(4) = 0.3`
पासे को दो बार फेका जाता है | मान लीजिए कि A तथा B क्रमशः घटनाओं प्रत्येक बार एक ही संख्या आना तथा B घटना कुल स्कोर 10 या 10 से अधिक आना को निरूपित करता है | निर्धारित कीजिए कि A तथा B स्वतंत्र घटनाएं है या नहीं
View SolutionA तथा B दो घटनाओं में से कम से कम एक के घटित होने की प्रायिकता 0.6 है। यदि A तथा B के एक साथ घटित होने की प्रायिकता 0.3 है, तो `P( barA ) + P(bar B )` का मान निकालिए।
View Solutionएक थैले में 5 लाल तथा 3 काले कंचे हैं। तीन कंचों को एक-एक करके बिना प्रतिस्थापित किए निकाला जाता है। निकाले गए तीन कंचों में से कम से कम एक कंचे के काले होने की प्रायिकता क्या है, यदि निकाला गया पहला कंचा लाल रंग का है?
View Solutionदो पासों को एक साथ फेंका जाता है और प्राप्त संख्याओं का योगफल नोट कर लिया जाता है। घटनाएँ E, F तथा G क्रमश: 'योगफल 4' 'योगफल 9 या 9 से अधिक' तथा 'योगफल संख्या 5 से भाज्य' को निरूपित करती हैं। P(E), P(F) तथा P(G) को ज्ञात कीजिए
View Solutionस्पष्ट कीजिए कि किसी सिक्के को तीन बार उछालने के परीक्षण को द्विपद बंटन रखने वाला क्यों कहा जाता है।
View SolutionA तथा B दो घटनाएँ ऐसी हैं कि `P(A) = (1)/(2), P(B)= (1)/(3)` तथा `P(A nnB)= (1)/(4)` ज्ञात कीजिए:
P(A|B)
View SolutionA तथा B दो घटनाएँ ऐसी हैं कि `P(A) = (1)/(2), P(B)= (1)/(3)` तथा `P(A nnB)= (1)/(4)` ज्ञात कीजिए:
P(B|A)
View SolutionA तथा B दो घटनाएँ ऐसी हैं कि `P(A) = (1)/(2), P(B)= (1)/(3)` तथा `P(A nnB)= (1)/(4)` ज्ञात कीजिए:
P(A'|B)
View SolutionA तथा B दो घटनाएँ ऐसी हैं कि `P(A) = (1)/(2), P(B) = (1)/(3)` तथा `P(A cap B) = 1/4`I ज्ञात कीजिए :
`P ( A' // B')`
View Solutionतीन घटनाओं A, B तथा C की प्रायिकताएँ क्रमश: `(2)/(5), (1)/(3)` तथा `(1)/(2)` हैं। दिया है कि `P(A nn C) = (1)/(5)` तथा `P(Bnn C)= (1)/(4)` P(C| B) तथा `P(A' nn C')` के मान ज्ञात कीजिए।
View Solutionमान लीजिए कि `E_(1)` तथा `E_(2)` दो स्वतंत्र घटनाएँ ऐसी हैं कि `p(E_(1)) = p_(1)` तथा `P(E_(2)) = p_(2)` निम्नलिखित प्रायिकताओं वाली घटनाओं का वर्णन शब्दों में कीजिए:
`p_(1)p_(2)`
View Solutionमान लीजिए कि `E_(1)` तथा `E_(2)` दो स्वतंत्र घटनाएँ ऐसी है कि `P(E_(1)) = p_(1)` तथा `P(E_(2)) = p_(2)` निम्नलिखित प्रायिकताओं वाली घटनाओं का वर्णन सब्दो में कीजिए :
View Solutionमान लीजिए कि `E_(1)` तथा `E_(2)` दो स्वतंत्र घटनाएँ ऐसी है कि `P(E_(1)) = p_(1)` तथा `P(E_(2)) = p_(2)` निम्नलिखित प्रायिकताओं वाली घटनाओं का वर्णन सब्दो में कीजिए :
View Solutionमान लीजिए कि `E_(1)` तथा `E_(2)` दो स्वतंत्र घटनाएँ ऐसी है कि `P(E_(1)) = p_(1)` तथा `P(E_(2)) = p_(2)` निम्नलिखित प्रायिकताओं वाली घटनाओं का वर्णन सब्दो में कीजिए :
View Solutionकिसी असंतत यादृच्छिक चर X का प्रायिकता बंटन नीचे दिया हुआ है:

k का मान ज्ञात कीजिए।
View Solutionकिसी असंतत यादृच्छिक चर X का प्रायिकता बंटन नीचे दिया हुआ है:

उपर्युक्त बंटन का माध्य ज्ञात कीजिए।
View Solutionसिद्ध कीजिए कि :
`P ( A ) = P ( A cap B) + P ( A cap bar( B) )`
View Solutionसिद्ध कीजिए कि:
`P(A uu B)= P(A nn B)+ P(A nn barB)+ P(barA nn B)`
View Solutionयदि यादृच्छिक चर X किसी सिक्के को तीन बार उछालने पर पट' आने की संख्या को निरूपित करता है, तो X का मानक विचलन ज्ञात कीजिए।
View Solutionएक पासे के खेल में, एक खिलाड़ी एक पासे के प्रत्येक फेंक के लिए 1 रुपये की हिस्सेदारी का भुगतान करता है। उसे 5 रुपये मिलते हैं यदि पासा 3 दिखाता है, रु 2 मिलते हैं यदि पासा 1 या 6 दिखाता है। थ्रो की लंबी श्रंखला में प्रति थ्रो प्रति खिलाड़ी का अपेक्षित लाभ क्या है?
View Solutionतीन पासों को एक साथ फेंका जाता है। तीनों पासों पर 2 आने की प्रायिकता ज्ञात कीजिए यदि यह ज्ञात है कि पासों पर प्रकट होने वाली संख्याओं का योग 6 है।
View Solutionकिसी लॉटरी के 10,000 टिकटों में से. प्रत्येक को र 1 का बेचा जाता है। प्रथम पुरस्कार र 3,000 को है तथा द्वितीय पुरस्कार 2,000 का है। इनके अतिरिक्त र500 वाले तीन अन्य पुरस्कार हैं। यदि आप एक टिकट खरीदते हैं, तो आप की प्रत्याशा (expectation) तया होगी ?
View Solutionएक थैले में 4 सफेद तथा 5 काली गेंद हैं। एक अन्य थैले में 9 सफेद तथा 7 काली गेंद हैं। पहले थैले से एक गेंद दूसरे थैले में स्थानांतरित कर दी जाती है। तत्पश्चात् दूसरे थैले में से एक गेंद यदृच्छया निकाली जाती है। इस बात की प्रायिकता ज्ञात कीजिए कि निकाली गई गेंद सफेद रंग की है।
View Solutionथैला I में 3 काली तथा 2 सफेद गेंद हैं और थैला II में 2 काली तथा 4 सफेद गेंद हैं। एक थैला तथा एक गेंद यादृच्छया छाँटे जाते हैं। काले रंग की गेंद के छाँटे जाने की प्रायिकता ज्ञात कीजिए।
View Solutionकिसी बाक्स में 5 नीली तथा 4 लाल गेंद हैं। एक गेंद यादृच्छया निकाली जाती है और प्रतिस्थापित नहीं की जाती है। उस गेंद का रंग भी नोट नहीं किया जाता है। तत्पश्चात् एक अन्य गेंद यादृच्छया निकाली जाती है। दूसरी गेंद के नीले रंग की होने की प्रायिकता क्या है?
View Solutionताश के 52 पत्तों की एक गड्डी से चार पत्ते बिना प्रतिस्थापन एक के बाद एक करके निकाले जाते हैं। सभी चारों पत्तों के "बादशाह " होने की प्रायिकता क्या है?
View Solutionएक पासा 5 बार फेंका जाता है। पासे पर ठीक तीन बार विषम संख्या आने की प्रायिकता ज्ञात कीजिए।
View Solutionदस सिक्के एक साथ उछाले जाते हैं। कम से कम 8 चित प्राप्त होने की प्रायिकता क्या है?
View Solutionकिसी व्यक्ति द्वारा लक्ष्य-भेदन की प्रायिकता 0.25 है। वह 7 बार लक्ष्य-भेदन का प्रयास करता है। उस व्यक्ति द्वारा कम से कम दो बार लक्ष्य भेदने की प्रायिकता क्या है?
View Solutionयह ज्ञात है कि 100 घड़ियों के एक ढेर में 10 घड़ियाँ खराब हैं। यदि 8 घड़ियाँ यादृच्छया, (एक-एक करके बिना प्रतिस्थापन के) चुनी जाती हैं, तो कम से कम एक खराब घड़ी चुनी जाने की प्रायिकता क्या है?
View Solutionएक यादृच्छिक चर X के नीचे दिये गए प्रायिकता बंटन पर विचार कीजिए।

`"Var"((X)/(2))`
View Solutionएक यादृच्छिक चर X के नीचे दिये गए प्रायिकता बंटन पर विचार कीजिए।

X का प्रसरण को परिकलित कीजिए।
View Solutionकिसी यादृच्छिक चर X का प्रायिकता बंटन नीचे दिया है।
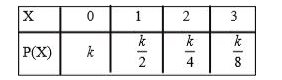
k का मान निर्धारित कीजिए,
View Solutionकिसी यादृच्छिक चर X का प्रायिकता बंटन नीचे दिया है।
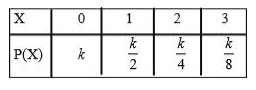
`P(X le 2)` तथा `P(X gt 2)` निर्धारित कीजिए
View Solutionकिसी यादृच्छिक चर X का प्रायिकता बंटन नीचे दिया है।
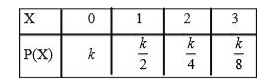
`P(X le 2) + P (X gt 2)` ज्ञात कीजिए ।
View Solutionनिम्नलिखित प्रायिकता बंटन के लिए यादृच्छिक चर X का मानक विचलन निर्धारित कीजिए:

View Solutionएक अनभिनत पासा इस प्रकार का है कि `P(4) = (1)/(10)` तथा अन्य स्कोर सम सम्भाव्य है। पासा दो बार उछाता जाता है। यदि 'पासे पर 4 प्रकट हेने की संख्या' X है, तो यादन्छिक नर X का प्रसरण ज्ञात कीजिए।
View Solutionएक पासा तीन बार फेका जाता है। मान लीजिए कि पासे पर 2 आने की संख्या X द्वारा निरूपित होती है। X की प्रत्याशा (expectation) ज्ञात कीजिए।
View Solutionदो अभिनत पासे एक साथ फेंके जाते हैं। पहले पासे के लिए `P(6) =(1)/(2)`, अन्य स्कोर समसम्भाव्य हैं, जबकि दूसरे पासे के लिए `P(1) = (2)/(5)` तथा अन्य स्कोर समसम्भाव्य हैं। '1 के प्रकट होने की संख्या' का प्रायिकता बंटन ज्ञात कीजिए।
View Solutionदो असंतत यादृच्छिक चर X तथा Y के प्रायिकता बटन निम्नलिखित हैं:

सिद्ध कीजिए की `E(Y^(2))= 2E(X)`
View Solutionएक कारखाने में बल्ब बनते हैं। किसी बल्ब के खराब होने की प्रायिकता `(1)/(50)` है तथा बल्बों 50 को दस-दस करके डिब्बों में पैक किया गया है । किसी एक डिब्बे के लिए निम्नलिखित प्रायिकता ज्ञात कीजिए:
कोई भी बल्ब खराब नहीं है
View Solutionएक कारखाने में बल्ब बनते हैं। किसी बल्ब के खराब होने की प्रायिकता `(1)/(50)` है तथा बल्बों 50 को दस-दस करके डिब्बों में पैक किया गया है । किसी एक डिब्बे के लिए निम्नलिखित प्रायिकता ज्ञात कीजिए:
ठीक दो बल्ब खराब हैं।
View Solutionएक कारखाने में बल्ब बनते हैं। किसी बल्ब के खराब होने की प्रायिकता `(1)/(50)` है तथा बल्बों 50 को दस-दस करके डिब्बों में पैक किया गया है । किसी एक डिब्बे के लिए निम्नलिखित प्रायिकता ज्ञात कीजिए:
8 से अधिक बल्ब ठीक काम करते हैं।
View Solutionमान लीजिए कि आपकी जेब में दो सिक्के हैं जो एक जैसे दिखाई देते हैं आपको ज्ञात है कि एक सिक्का अनभिनत (न्याय्य) है तथा दूसरे सिक्के में दोनों ओर 'चित' (2-headed) है। यदि आप एक सिक्का निकाल कर उछालते हैं और 'चित' प्राप्त करते हैं, तो इस बात की प्रायिकता क्या है कि यह सिक्का न्याय्य है?
View Solutionमान लीजिए कि रुधिर वर्ग O वाले लोगों में 6% वामहस्तिक (left handed) हैं और अन्य रुधिर वर्ग वाले लोगों में 10% वामहस्तिक हैं। 30% लोगों का रुधिर वर्ग 0 है । यदि एक वामहस्तिक व्यक्ति यादृच्छया चुना जाता है, तो इस बात की प्रायिकता क्या है कि उसका रुधिर वर्ग O है?
View Solutionसमुच्चय S= 1, 2. 3...... n से दो प्राकृत संख्याएँ r , s, एक बार में एक, बिना प्रतिस्थापन के, निकाली जाती हैं। `P[r le p | s le p]`, जहाँ `p in S` ज्ञात कीजिए ।
View Solutionजब एक पासे को दो बार फेंका जाता है तो प्राप्त दो स्कोरों में से महत्तम स्कोर का प्रायिकता बंटन ज्ञात कीजिए। बंटन का माध्य भी निर्धारित कीजिए।
View Solutionएक यादृच्छिक चर X केवल 0, 1, 2 गाना को धारण कर सकता है। दिया हुआ है फि PX = 0) = P(X = 1) = p तथा यह कि `E(X^(2)) = E[X]`, तो p ना मान ज्ञात कोजिए।
View Solutionनिम्नलिखित बंटन का प्रसरण ज्ञात कीजिए:
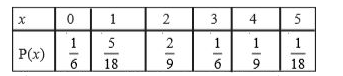
View SolutionA और B एकान्तरत : एक पासे के जोड़े को उछालते है यदि B के 7 फेकने से पहले A ,6 फेकता है तब A जीतता है तथा यदि A के फेकने से पहले बी ,7 फेकता है तब B जीतता है यदि A खेलता प्रारंभ करे तो A के जितने की प्रायिकता ज्ञात कीजिए
View Solutionदो पासे उछाले जाते हैं । ज्ञात कीजिए कि क्या निम्नलिखित दो घटनाएँ A तथा B स्वतंत्र हैं: A = (x, y) : x+y=11 B = (x, y) :x ≠5 जहाँ (x, y) एक विशिष्ट प्रतिदर्श बिंदु को नि रूपित करते हैं ।
View Solutionएक पात्र में m सफेद और n काली गेंद है। एक गेंद यदृच्छया निकाली जाती है और उसे उसी रंग की k अतिरिक्त गेंदों के साथ पात्र में वापस रख दिया जाता है । पुनः एक गेंद यदृच्छया निकाली जाती है। निकाली गई गेंद के सफेद होने की प्रायिकता ज्ञात कीजिए।
View Solution
प्रश्नावली (लघु उत्तरीय प्रश्न (S.A.)) questions and complete solutions for chapter प्रायिकता of NCERT EXEMPLAR HINDI of Class 12