Complete Solutions to Probability of chapter PROBABILITY of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | PROBABILITY |
| NCERT EXEMPLAR | Probability |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
For a loaded die, the probabilities of outcomes are given as under: `P(1)=P(2)=2/(10),P(3)=P(5)=P(6)=1/(10)a n dP(4)=3/(10)` The die is thrown two times. Let A and B be the events as defined below A=Getting same number each time, B=Getting a total score of 10 or more. Determine whether or not A and B are independent events.
View SolutionRefer to question 1 above. If the die were fair, determine whether or not the events A and B are independent.
View SolutionThe probability that atleast one of the two events A and B occurs is 0.6. If A and B occur simultaneously with probability 0.3, evaluate `P(barA)+P(barB)`.
View SolutionA bag contains 5 red marbles and 3 black marbles. Three marbles are drawn one by one without replacement. What is the probability that atleast one of the three marbles drawn be black, if the first marble is red?
View SolutionTwo dice are thrown together and the total score is noted. The event E, F and G are a total 4, a total of 9 or more, and a total divisible by 5, respectively. Calculate `P(E),P(F)a n dP(G)` and decide which pairs of events, if any, are independent.
View SolutionExplain why the experiment of tossing a coin three times is said to have Binomial distribution.
View SolutionIf A and B are two events such
`P(A)=1/2,P(B)=1/3and P(AcapB)=1/4`,then find
(i) P(A/B). (ii) P(B/A).
(iii) P(A'/B). (iv) P(A'/B').
View SolutionThree events A, B and C have probalities `2/5,1/3 and 1/2`, respectively. If, `P(AcapC)=1/5and P(BcapC)=1/4`, then find the values of P(C/B) and `P(A'capC')`
View SolutionLet `E_(1) and E_(2)` be two independent events such that `P(E_(1))=P_(1)` and `P(E_(2))=P_(2)`, describe in words of the events whose probabilities are
(i) `P_(1)P_(2)` (ii) `(1-P_(1))P_(2)`
(iii) `1-(1-P_(1))(1-P_(2))` (iv) `P_(1)+P_(2)-2P_(1)P_(2)`
View SolutionA discrete random variable X has the probability distribution as given below
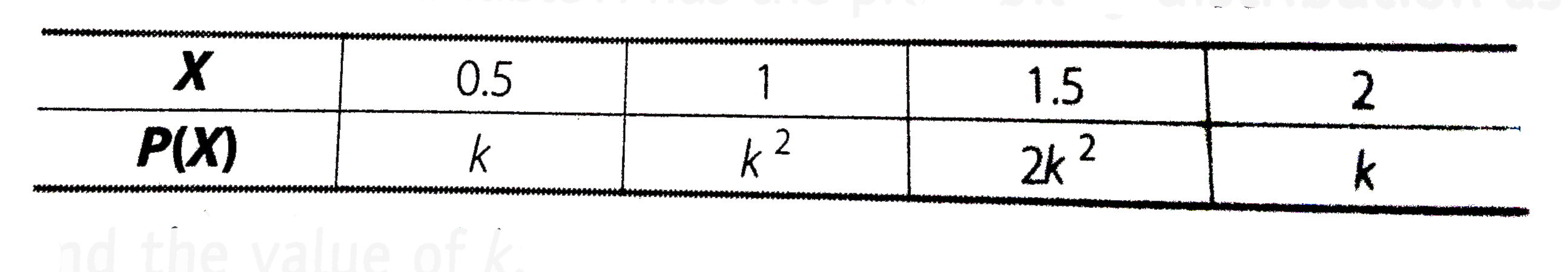
(i) Find the value of k.
(ii) Determine the mean of the distribution.
View SolutionProve that
(i) `P(A)=P(AcapB)+P(AcapbarB)`
(ii) `P(AcupB)=P(AcapB)+P(AcapbarB)+P(barAcapB)`
View SolutionIf x is the number of tails in three tosses of a coin, then determine the standard deviation of X.
View SolutionIn a dice game , a player pays a stake of ₹1 for each throw of a die. She receives ₹5, if the die shows a 3, ₹ 2, if the die shows a 1 or 6 and nothing otherwise, then what is the player's expected profit per throw over a long series of throws?
View SolutionThree dice are thrown at the same time. Find the probability of getting three two's, if it is known that the sum of the numbers on the dice was 6
View SolutionSuppose 10000 tickets are sold in a lottery each for ₹ 1. First prize is of ₹ 1. First prize is of ₹ 3000 and the second prize is of ₹ 2000. There are three third prizes of ₹ 500 each. If you buy one ticket, then what is your expectation?
View SolutionA bag contains 4 white and 5 black balls. Another bag contains 9 white and 7 black balls. A ball is transferred from the first bag to the second and then a ball is drawn at random from the second bag. Find the probability that the ball drawn is white.
View SolutionA bag contains 3 white and 2 black balls and another bag contains 2 white and 4 black balls. One bag is chosen at random. From teh selected bag, one ball is drawn. find the probability that the ball drawn is white.
View SolutionA box has 5 blue and 4 red balls. One ball is drawn at random and replaced. Its colour is also not noted. Then, another ball is drawn at random. What is the probability of second ball being blue?
View SolutionFour cards are successively drawn without replacement from a deck of 52 playing cards. What is the probability that all the four cards are king?
View SolutionIf a die is thrown 5 times, then find the probability that an odd number will come up exactly three times.
View SolutionIf ten coins are tossed, then what is the probability of getting atleast 8 heads?
View SolutionThe probability of a man hitting man hitting target is 0.25. If he shoots 7 times, then what is the probability of his hittiing atleast twice ?
View SolutionA lot of 100 watches is known to have 10 defective watches. If 8 watches are selected (one by one with replacement) at random, then what is the probability that there will be atleast one defective watch ?
View SolutionConsider the probability distribution of a random variable X

Calculate
(i) `V( X/2)` (ii) Variance of X.
View SolutionThe probability distribution of a random variable X is given below
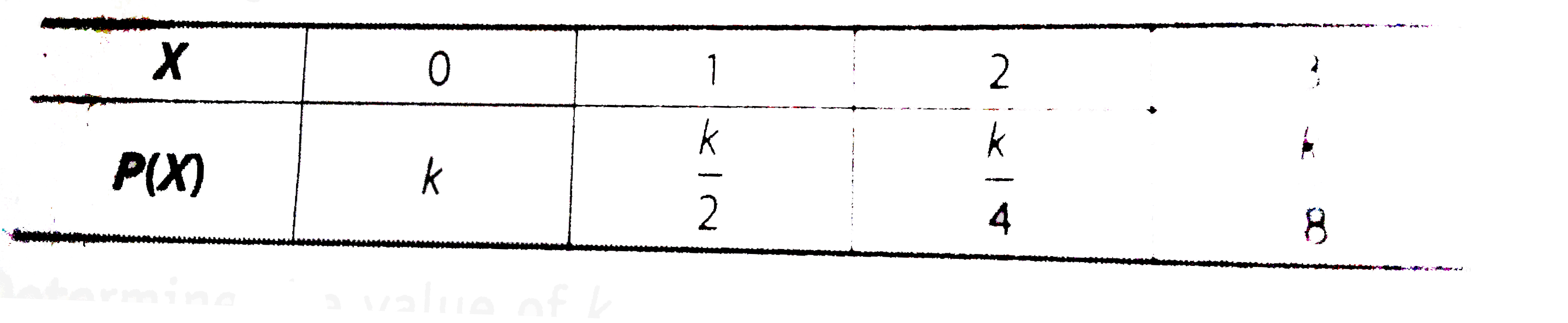
(i) Determine the value of K .
(ii) Determine `P(Xle2)andP(Xgt2)`.
(iii) Find P`(Xle2)+P(Xgt2)`.
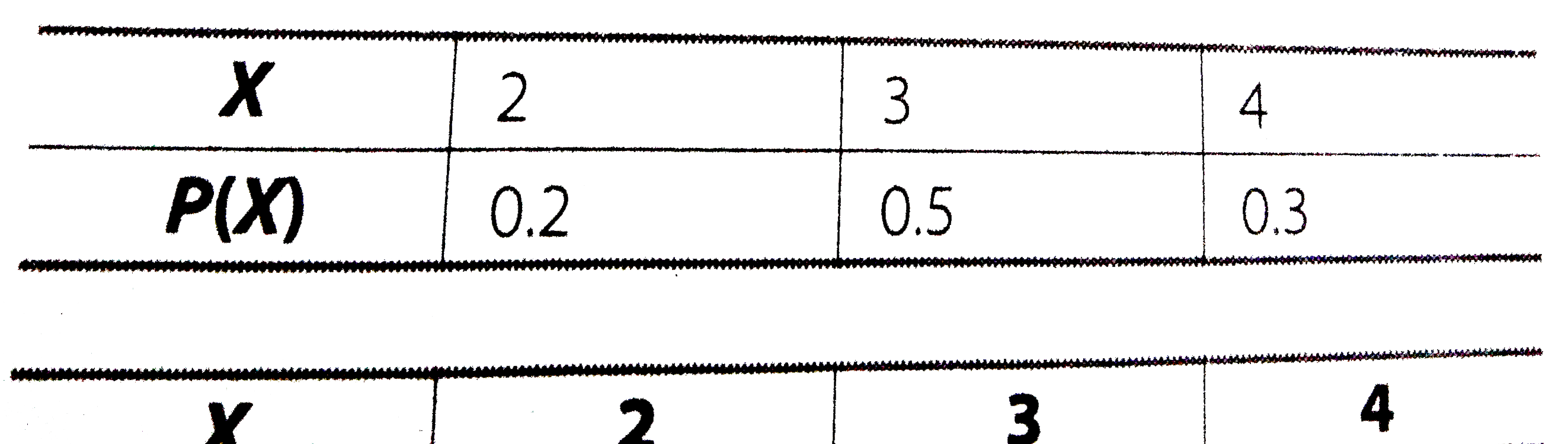
View SolutionFor the following probability distribution determine standard deviation of the random variable X.
View SolutionA biased die is such that P(4)`=1/10` and other scores being equally likely. The die tossed twice. If X is the number of four seen, then find the variance of the random variable X.
View SolutionA die is thrown three times. Let `X` be the number of twos seen. Find the expectation of `X` .
View SolutionTwo baised dice are thrown together. For the first die `P(6)=1/2` , other scores being equally likely while for the second die, `P(1)=2/5` and other scores are equally likely. Find the probability distribution of the number of ones seen.
View SolutionTwo probability distributionof the discrete random variable X and Y are given below.

Prove that `E(Y^(2))=2E(X)`.
View SolutionA factory produces bulbs. The probability that any one bulb is defective is `1/50` and they are packed in 10 boxes. From a single box, find the probability that
(i) none of the bulbs is defective.
(ii) exactly two bulbs are defective.
(iii) more than 8 bulbs work properly.
View SolutionSuppose you have two coins which appear identical in your pocket. You know that one is fair and one is 2-headed. If you take one out, toss it and get a head, what is the probability that it was fair coin?
View SolutionSuppose that 6% of the people with blood group O are left handed and 10% of those with other blood groups are left handed, 30 % of the people have blood groups O. If a left handed person os selected at random, what is the probability that he/she will have blood group O?
View SolutionIf two natural numbers r and s are drawn one at a time, without replacement from the set S={1,2,3,….n}, then find P`(rlep|slep)` where p`in`S.
View SolutionFind the probability distribution of the maximum of two scores obtained when a die is thrown twice. Determine also the mean of the distribution.
View SolutionThe random variable X can take only the values 0,1,2. If
`P(X=0)=P(X=1)=p and E(X^(2))=E[X]`,
then find valu of p.
View SolutionFind the varience of the following distribution.
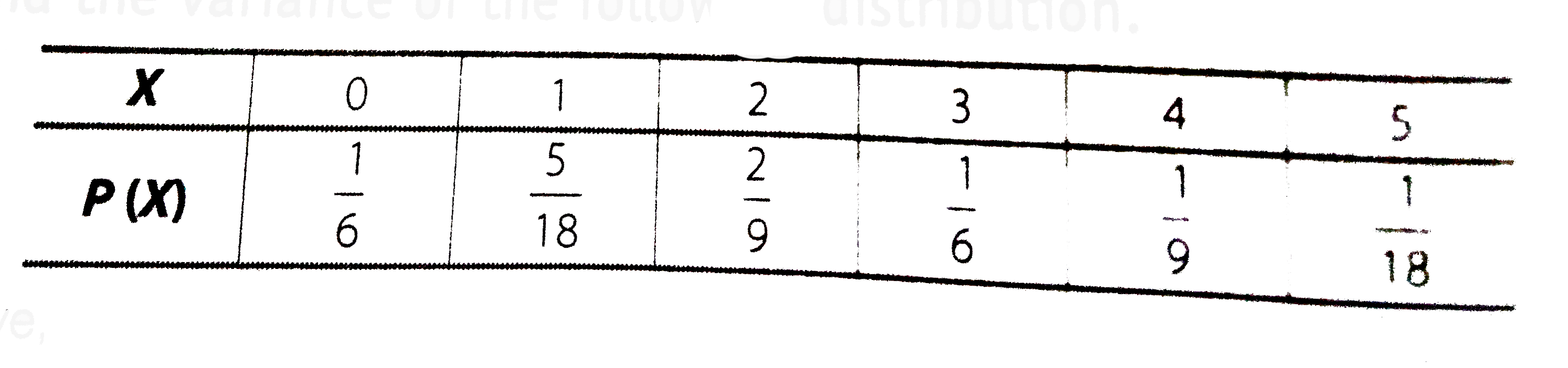
View SolutionA and B throw a pair of dice alternately. A wins the game, if he gets a total of 6 anfd B wins, if she gets a total of 7. If a starts the game, then find the probabbility of winning the game by A in third throw of the pair of dice.
View SolutionTwo dice are tossed. Find whether the following two events A and B are independent A={(x,y):x+y=11} and B={(x,y):`xne5`}, where (x,y) denotes a typical sample point.
View SolutionAn urn contains m white and n black balls. A ball is drawn at random and is put back into the urn along with k balls of the same colour as that of the ball drawn. a ball is again drawn at random. Show that the probability of drawing a white ball now does not depend on k.
View SolutionThree bags contain a number of red and white balls as follows Bag I : 3 red balls, Bag II : 2 red balls and 1 white balls and Bag III : 3 white balls. `i/6`, where i=1,2,3. What is the probability that
(i) a red ball will be selected? (ii) a white ball is selected?
View SolutionRefer to question 41 above. If a white ball is selected, what is the probability that it come from ltbr?. (i) Bag II? (ii) Bag III?
View SolutionA shopkepper sells three types of flower seeds `A_(1),A_(2) and A_(3)`. They are sold as mixture, where the proportion are 4 : 4 : 2, respectively. The germination rates of the three types of seeds 45%, 60% and 35%. Calculate the probability
(i) of a randomly chosen seed to germinate.
(ii) that it will not germinate given that the seed is of type `A_(3)`.
(iii) that it is of the type `A_(2)` given that a randomly chosen seed does bot germinate
View SolutionA letter is known to have come either from 'TATA NAGAR or from 'CALCUTTA'. On the envelope, just two consecutive letter came from 'TATA NAGAR'?
View SolutionThere are two bags,one of which contains 3 black and 4 white balls while the other contains 4 black and 3 white balls. A die is thrown. If it shows up 1 or 3, a ball is taken from the Ist bag but it shows up any other number, a ball is chosen from the II bag. Find the probability of choosing a black ball.
View SolutionThere are three urns containing 2 white and 3 black balls, 3 white and 2 black balls and 4 white and 1 black balls, respectively. There is an equal probability of each urn being chosen. A ball is drawn at random from the chosen urn and it is found to be white. Find the probability that the ball drawn was from the second urn.
View SolutionBy examining the chest X-ray, probability that T.B is detected when a person is actually suffering is 0.99. the probability that the doctor diagnoses incorrectly that a person has T.B. on the basis of X-ray is 0.001. in a certain city 1 in 100 persons suffers from T.B. A person is selected at random is diagnosed to have T.B. What is the chance that he actually has T.B.?
View SolutionAn item is manufactured by three machines A, B and C. Out of the total member of items manufactured during a specified period, 50% are manufactured on A, 30% on B and 20% on C. 2% of the items produced on A and 2% of items produced on B are defective and 3% of these produced on C are defective. All the items are stored at one godown. One item is drawn at random and is found to be defective. What is the probability that it was manufactured on machine A?
View SolutionLet X be a discrete random variable whoose probability distribution is defined as follows.
`P(X=x)={{:(k(x+1)",for x=1,2,3,4"),(2kx", for x=5,6,7"),(0", otherwise"):}`
where,k is a constant. Calculate (i) the value of k. (ii) E (X).
(ii) standard deviation of X.
View SolutionThe probability distribution of a discrete random variable x is given as under

Calculate
(i) the value of A, if E(X)=2.94.
(ii) variance of X.
View SolutionThe probability distribution of a random variable x is given as under
`P(X=x)={{:(kx^(2),x="1,2,3"),(2kx,x="4,5,6"),("0,","otherwise"):}`
where, k is a constant. Calculate
(i) E(X) (ii) `E(3X^(2))` (iii) `P(Xge4)`
View SolutionA bag contains `(2n+1)` coins. It is known that `n` of these coins have a head on both sides whereas the rest of the coins are fair. A coin is picked up at random from the bag and is tossed. If the probability that the toss results in a head is `(31)/(42)` , determine the value of `n` .
View SolutionTwo cards are drawn successively without replacement from a well shuffled deck of cards . Find the mean and standard variation of the random variable X , where X is the number of aces .
View SolutionA die is tossed twice . If a success is getting an even number on a toss , then find the variance of the number of successes .
View SolutionThere are 5 cards numbered 1 to 5 , one number on one number on one card . Two cards are drawn at random without replacement . Let X denotes the sum of the numbers on two cards drawn . Find the mean and variance of X.
View SolutionIf P(A)=`4/5` and P(`AcapB`)=`7/10`, then `P(B//A)` is equal to
View SolutionIf `P(AcapB)=7/10 and P(B)=17/20`,then P(A/B) equals to
View SolutionIf `(A)=3/10,P(B)=2/5 and P(AcupB)=3/5` then P(B/A)+P(A/B) equals to
View SolutionIf `P(A)=2/5,P(B)=3/10andP(AcapB)=1/5` then P(A'/B')`cdot`P(B'/A') is equal to
View SolutionIf A and B are two events such that P(A)=`1/2,P(B)=1/3and P(A//B)=1/4`,then `P(A'//B')` equals to
View SolutionIf P(A)=0.4,P(B)=0.8 and P(B/A)=0.6, then `P(AcupB)` is equal to
View SolutionIf A and B are two events and A`nephi,Bnephi` , then
View SolutionIf A and B are events such that P(A)=0.4,P(B)=0.3and`P(AcupB)=0.5` then `P(B'capA)` equals to
View SolutionIf A and B are two events such that `P(B)=3/5,P(A//B)=1/2` and `P(AcupB)=4/5`, then P(A) equals to
View SolutionIn question 64 (above),P(B/A') is equal to
View SolutionIf P(B)`=3/5,P(A//B)=1/2andP(AcupB)=4/5`, then `P(AcupB)'+P(A'cupB)` is equal to
View SolutionIf `P(A)=7/13,P(B)=9/13`and `P(AcapB)=4/13`, then P(A'/B) is equal to
View SolutionIf A and B are suchg that events that `P(A)gt0andP(B)ne1`, then `P(A'//B')` equals to
View SolutionIf A and B are two events with with `P(A)=3/5` and `P(B)=4/9`, then `P(A'capB')` equals to
View SolutionIf two events are independent, then
View SolutionIf A and B be two events such that P(A)`=3/8,P(B)=5/8` and `P(AcupB)=3/4` then P(A/B).P(A'/B) is equal to
View SolutionIf the events A and B are independent, then `P(AcapB)` is equal to
View SolutionTwo events E and F are independent. If `P(E )=0.3` and `P(EcupF)=0.5` then `P(E//F)-P(F//E)` equals to
View SolutionA abg contains 5 red and blue balls. If 3 balls are drawn at random without replacement, them the probability of getting exactly one red ball is
View SolutionA bag containing 5 red and 3 blue balls. If 3 balls are drawn at random without replacement the probability that exactly two of the three balls were red, the first being red is
View SolutionThree persons `A,B` and `C`, fire at a target in turn, starting with `A`. Their probability of hitting the target are `0.4, 0.3` and `0.2`, respectively. The probability of two hits is
View SolutionAssume that in a family, each child is equally likely to be a boy or girls .A family with three children is is choosen at random. The probability that the eldest child is a girls given that the family has at least one girls is
View SolutionIf a die is thrown and a card is selected at random from a deck of playing cards, than the probability of getting an even number on the die and a spade card is
View SolutionA box contains 3 orange balls, 3 green balls and 2 blue balls. Three balls are drawn at random from the box without replacement. The probability of drawing 2 green balls an one blue ball is
View SolutionA flashlight has 8 batteries out of which 3 are dead. If two batteries selected without replacement and tested, then probability that both are dead is
View SolutionIf eight coins are tossed together, then the probability of getting exactly 3 heads is
View SolutionTwo dice are thrown. If it is known that the sum of numbers on the dice was less than 6, the probability of getting a sum 3, is
View SolutionWhich one is not a requirement of a binomial distribution?
View SolutionIf two cards are drawn from a well shuffled deck of 52 playing cards with replacement, then the probability that both cards are queens, is
View SolutionThe probability of guessing correctly atleast 8 out of 10 answers on a true falsetype examination is
View SolutionIf the probability that a person is not a swimmer is 0.3, then the probability that out of 5 persons 4 are swimmers is
View SolutionThe probability distribution of a discrete random variable X is given below

The value of k is
View SolutionFor the following probability distribution.
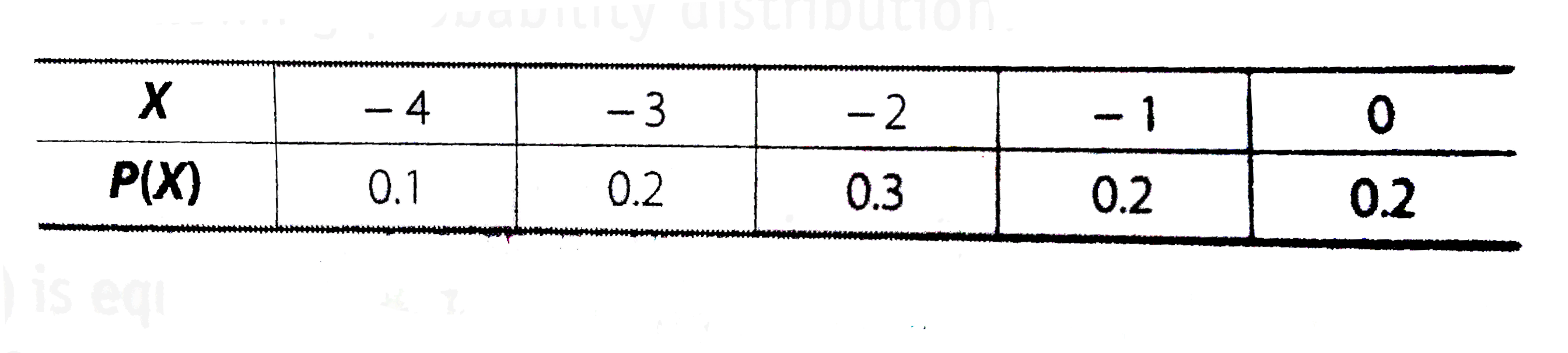
E(X) is equal to
View SolutionFor the following probability distribution.
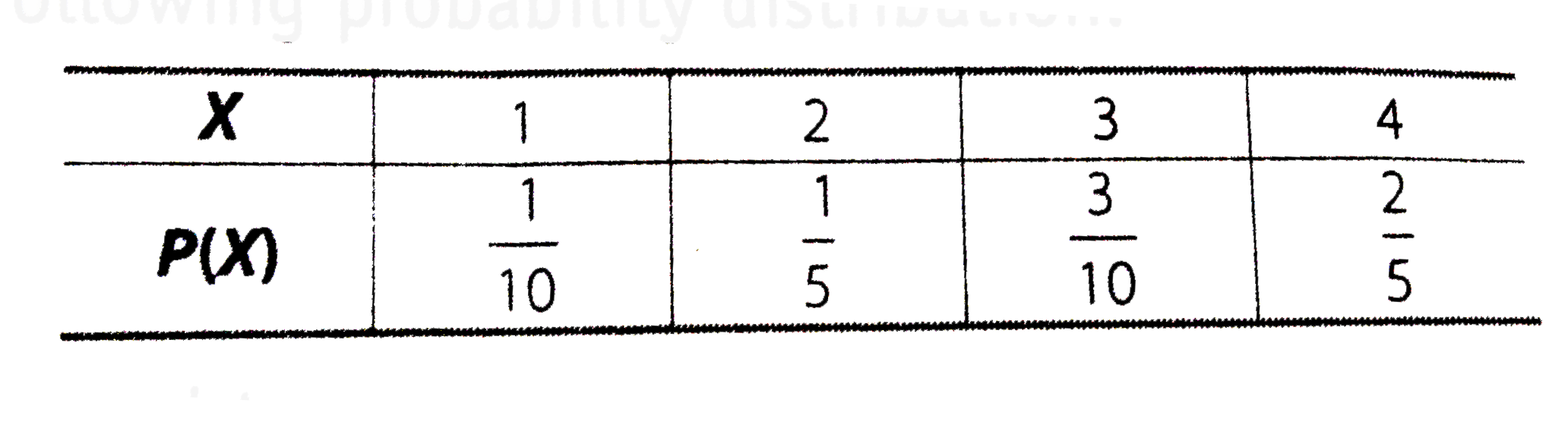
`E(X^(2))` is equal to
View SolutionSuppose a random variable X follows the binomial distribution with parameters n and p, where `0
View SolutionIn a college, 30% students fail in physics, 25% fail in Mathematics and 10% in both. One student is choosen at random. The probability that she fails in physics, if she has failed in Mathematics is
View SolutionA and B are two students. Their chances of solving a problem correctly are `1/3 and 1/4`, respectively If the probability of their making a common error is, 1/20 and the obtain the same answer, then the probability of their answer to be correct is
View SolutionIf a box has 100 pens of which 10 are defective, then what is the probability that out of a sample of 5 pens drawn one by one with replacement atmost one is defective?
View SolutionIf P(A)`gt`0 and P(B)`gt`0. Then A and B can be both mutually exclusive and independent.
View SolutionIf A and B are independent events, then A' and B' are also independent.
View SolutionIf A and B are mutually exclusive events, then they will be independent also.
View SolutionTwo independent events are always mutually exclusive.
View SolutionIf A and B are two independent events, then P( A and B)=P(A)`cdot`P(B)
View SolutionAnother name for the mean of a probability distribution is expected value.
View SolutionIf A and B' are independent events, then `P(A'cupB)=1-P(A)P(B')`.
View Solution
Probability questions and complete solutions for chapter PROBABILITY of NCERT MATHS (HINGLISH) of Class 12