Complete Solutions to वस्तुनिष्ठ प्रकार प्रशन of chapter वैधुत फ्लेक्स तथा गौस की प्रमेय of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | वैधुत फ्लेक्स तथा गौस की प्रमेय |
| KUMAR MITTAL | वस्तुनिष्ठ प्रकार प्रशन |
| Number Of Questions | 23 |
| Academic Year | 2023-24 |
L मीटर भुजा का वर्गाकार शेरेस्ट कागज के टेल में है एक एकसमान विधुत क्षेत्र `hat E` वाल्ट/कॉलम भी कागज के तेल में वर्गाकार शेरेस्ट के निचे के आधे भाग में सीमित है SI मात्रक में षेरेस्ट से सम्भंदित विधुत फ्लेक्स है

View Solutionमाना एक विधुत क्षेत्र `hat E=E_(0) hat X` है जहाँ `E_(0)` नियतांक है इस क्षेत्र के कारण चित्र में दर्शाये आच्छादित क्षेत्र से गुजरने वाला विधुत फ्लेक्स है

View Solutionविधुत आवेश `+q_(1)-q_(1)` तथा `+q_(2)` निवृत्त में रखे गए है तहा S एक गोलिये गोशिये षेरेस्ट है षेरेस्ट S से गुजरने वाले विधुत फ्लेक्स है

View Solutionत्रिजिये `a//4` की एक डिस्क पर 6C आवेश एकसमान रूप से वितरित है और यह X-Y तल में इस प्रकार रखी है की इसके केंद्र `((-1)/(2),0,0)` पर है a लम्बाई की एक छान जिस पर 8C आवेश एकसमान रूप से वितरित है X अक्ष पर `x=a//4` से `x=5a//4` तक में रखी है दो बिंदु आवेश -7C तथा 3C क्रमश `((a)/(4),(a)/(4),0)` तथा `((-3a)/(4),(3a)/(4),0)` पर रखे है एक घनिए 6 सतह रहा विधुत फ्लेक्स है `x=pm(a)/(2),y=pa(a)/(2),z=px(a)/(2)` बनी है इस घनिए सता से गुजर रहा विधुत फ्लेक्स है
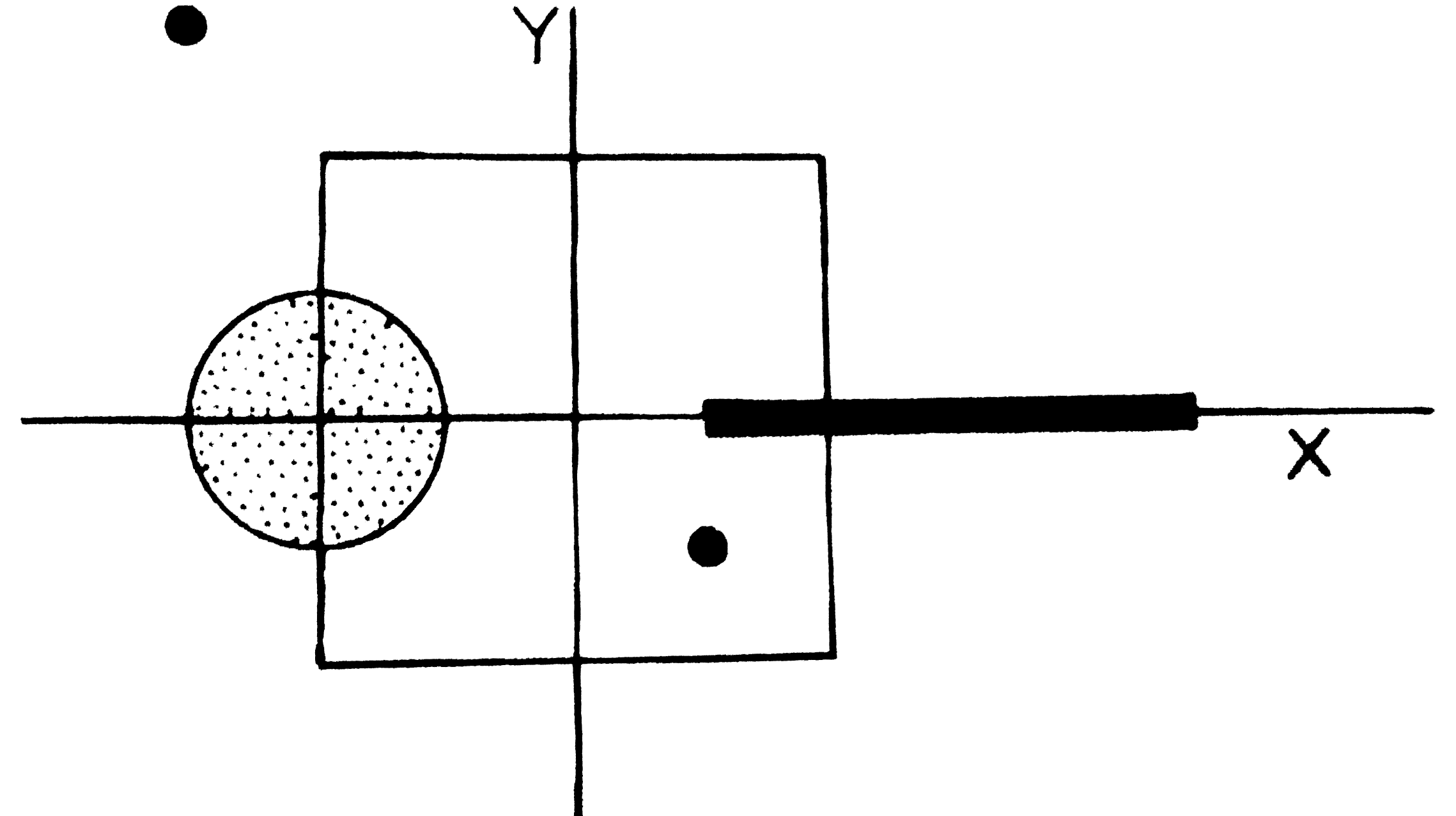
View Solutionतीन अनाथ की आवेश की चादर X-Y तल में परस्पर समांतर रखी है जिनके एकसमान आवेश घनत्व चित्रानुसार है बिंदु P पर विधुत क्षेत्र है

View Solutionएक तल पर एकसमान रूप से अवश्य अननाथ लम्बाई की दो आचलक प्लेट परस्पर `90^(@)` पर काटती है उनके आवेश के षेरेस्ट घनत्व `+sigma` व `sigma` है दोनों के बीच के इस्थान में किसी बिन्दु पर विधुत की त्रीवता है
View Solutionएकसमान रूप से आवेशित R त्रिजिये की एक पतली गोलिये कोस का शीर्ष आवेश घनत्व `sigma` है यह कोस दो अर्द्गोलकर कोसो को F बल दुवारा एक दुस्तरे से सटाकर रकने से बना है F किसके अनुक्रमानुपाती होगा

View Solutionएक गोलिये शुचालक के ब्रह्म षेरेस्ट पर 0.036 न्यूटन / कॉलम का विधुत उत्पान करने के लिए शुचालक पर डेल जाने वाले एलेक्ट्रोनो की संख्या है
View Solution`R_(1)` व `R_(2)` त्रिजियो के दो चालक गोलों के षेरेस्ट पर आवेशों के षेरेस्ट घनत्व बराबर है षेरेस्ट पर विधुत क्षेत्र की त्रिवताओ का अनुपात है
View Solutionकिसी इस्थान में विधुत क्षेत्र त्रिज्यीय है तथा इसका दिशा भर की और है तथा इसका मान E=Ar से निरूपित किया जाता है एक ऐसे गोले पर जिसकी त्रिजिये a है और जिसका केंद्र इस क्षेत्र के मूल बिंदु पर है आवेश की मात्रा होगी
View Solutionधातु का बना एक ठोस गोले एकसमान विधुत क्षेत्र में रेखा है चित्र में दिखाई गई बल रेखाओ में से सही बल रेखा
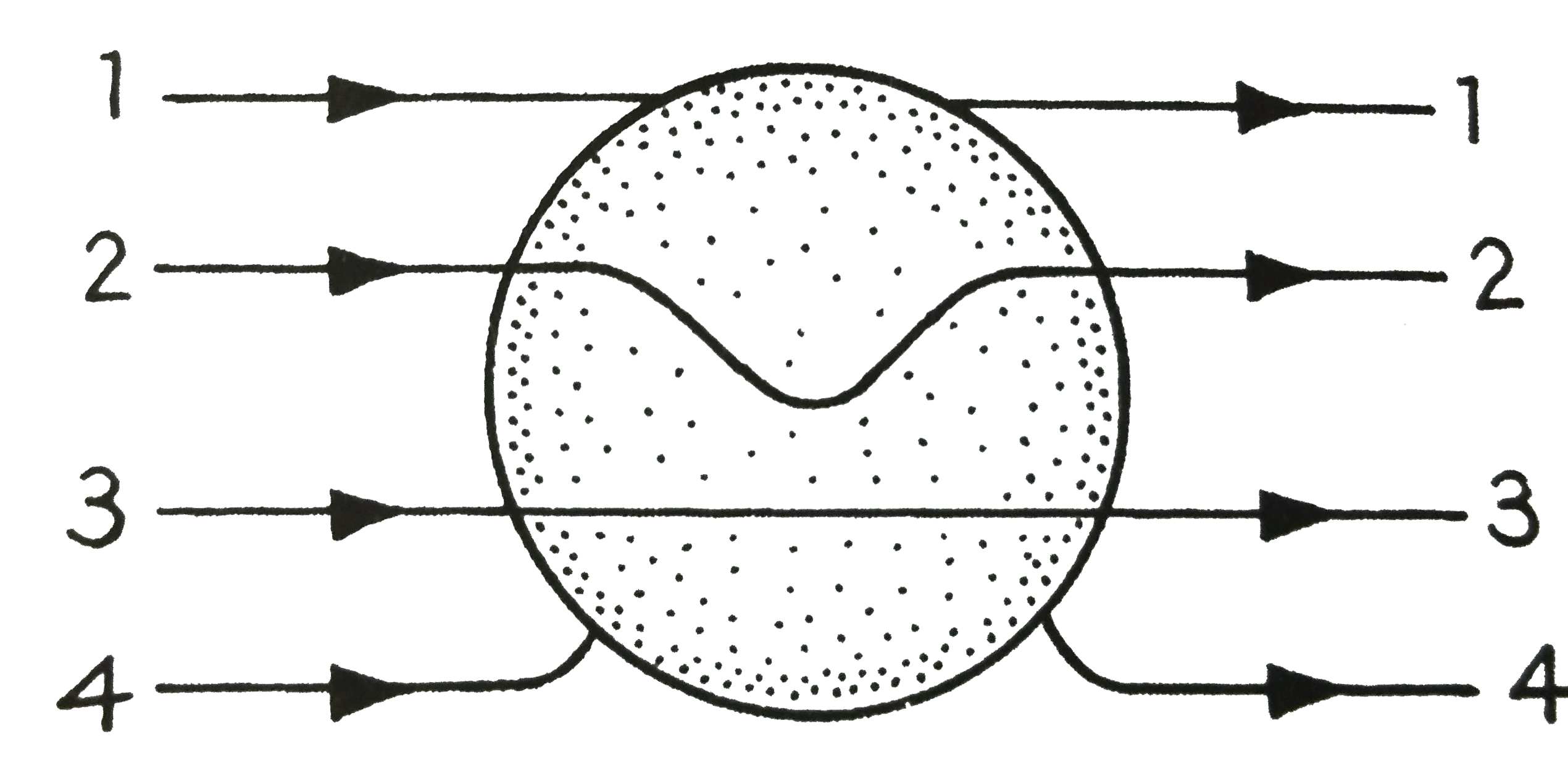
View Solutionएक धातु कोश (Metallic shell) की गुहिका (Cavity) में एक बिन्दु आवेश ४ स्थित है। नीचे दी गई आकृतियों में से किस आकृति द्वारा वैद्युत बल रेखायें सही रूप में प्रदर्शित होंगी ?
View Solutionधातु के बने R,2R तथा 3 R त्रिज्याये वाले तीन खोखले सेकेंडरी गोलों को क्रमशः `Q_(1),Q_(2)` तथा `Q_(3)` आवेश दिए जाते है तीनो गोले की बाहरी सतह पर आवेश के घनत्व बराबर पाए जाते है तब दिए गए आवेशों का अनुपात `Q_(1):Q_(2):Q_(3)` होगा
View Solutionएक ठोस से जिसके आयतन में आवेश एकसमान रूप से वितरित है चित्र में दिखाए अनुसार एक गोलाकार भाग हटा दिया गया है खाली किये गए स्थान में विधुत क्षेत्र है

View Solutionत्रिजिये R तथा सम्पूर्ण q वाले एकसमान आवेशित गोले से विधुत क्षेत्र को गोले के केंद्र से दुरी r के फलन के रूप में ऑरेककिलित किया गया है सांगत सही ग्राफ सा होगा
View Solutionत्रिज्या `R_(1)` का एकसमान आवेश घनत्व का गोलाकार आवेश मूल बिंदु O पर केंद्रित है इस वितरण में त्रिज्या `R_(2)` तथा P पर केंद्रित एक गोलाकार गुहिका जहाँ दूरी OP `a=R_(1)-R_(2)` है बनाई जाती है यदि गुहिका के अंदर स्थित `hat r` पर विधुत क्षेत्र `hat E` है तब सही कथन है
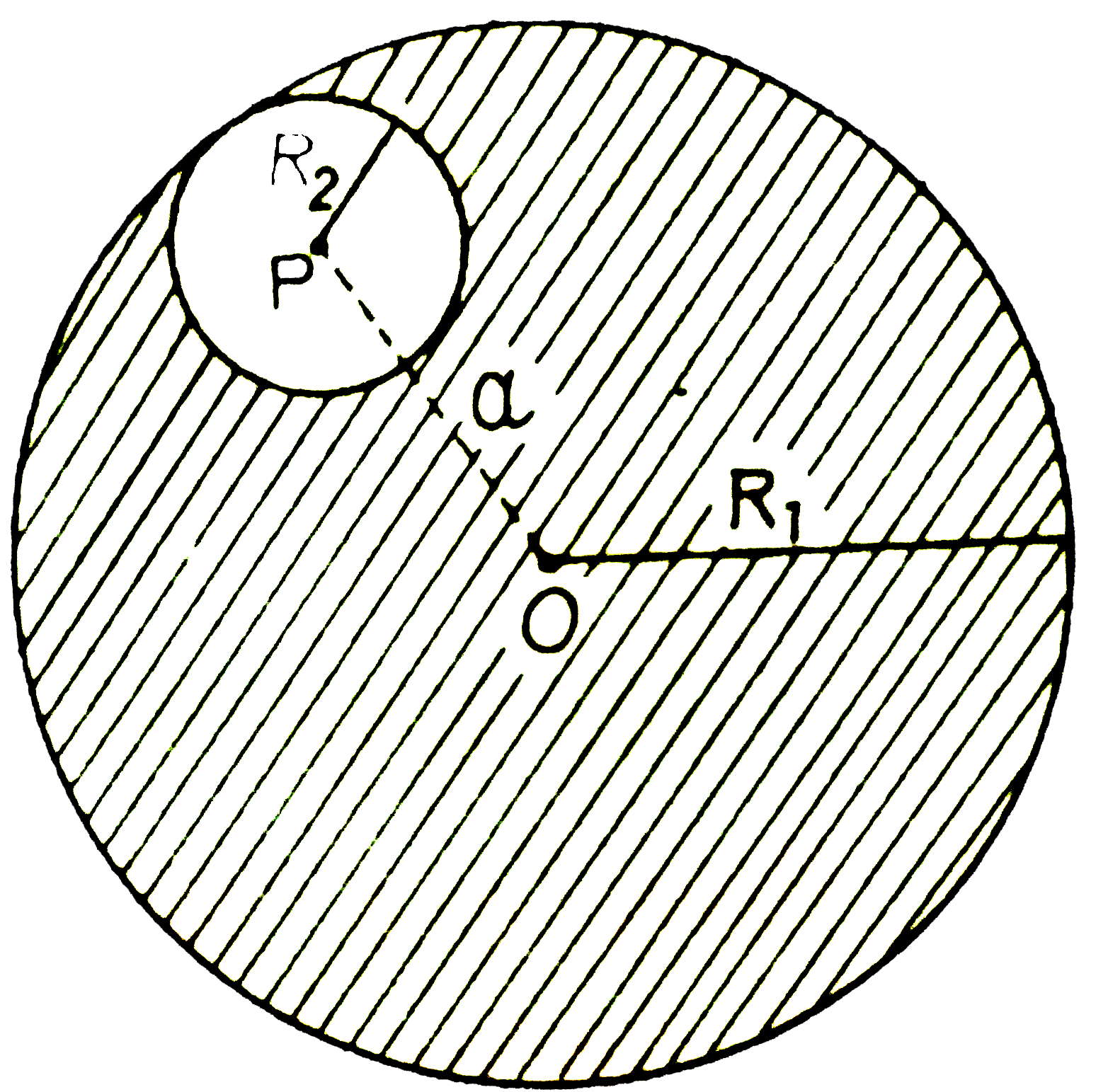
View Solution10 सेमी त्रिज्या का एक चालक गोले 1 `mu C` से आवेशित किया गया है इसके कारण अधिकतम विधुत क्षेत्र की तीव्रता मान है
View Solutionमाना की `rho (R )=(Q)/(piR^(4)).R` त्रिज्या के एक ठोस गोले में आवेश का वितरण बताता है जिस पर कुल आवेश Q है गोले के केंद्र से गोले के भीतर `r_(1)` दुरी पर एक बिंदु P है इस बिंदु पर विधुत क्षेत्र की त्रीवता का परिमाण है ?
View Solutionनिम्न चित्र में दर्शाये गए तीन प्रावधूत गोले पर जिनकी त्रिजिये क्रमश `R//2,R,2R ` है ,आवेश क्रमश Q,2Q व 4Q सामान रूप से वितरित है | यदि बिंदु पर जो प्रत्येक गोले के केंद्र से R दुरी पर है, गोले 1,2 तथा 3 की कारण विधुत क्षेत्र परिदम क्रमश `E_(1),E_(2)` तथा `E_(3)` है

View Solutionएक गोले जिसकी त्रिजिये R है आवेश का आयतन घनत्व `rho=k r` है जहाँ r गोले के केंद्र से दुरी है तथा k नियतांक है गोले की षेरेस्ट पर विधुत क्षेत्र की त्रीवता का परिमाण है
View Solutionत्रिज्या a तथा b के दो संकेन्द्री गोले के बीच के स्थान में आयतन आवेश घनत्व `rho=A//r` है जहाँ A स्थिरांक है तथा r केंद्र से दूरी है गोले के केंद्र पर एक बिंदु आवेश Q है A का वह मान बताये जिससे गोले के बीच के स्थान में एकसमान विधुत क्षेत्र हो
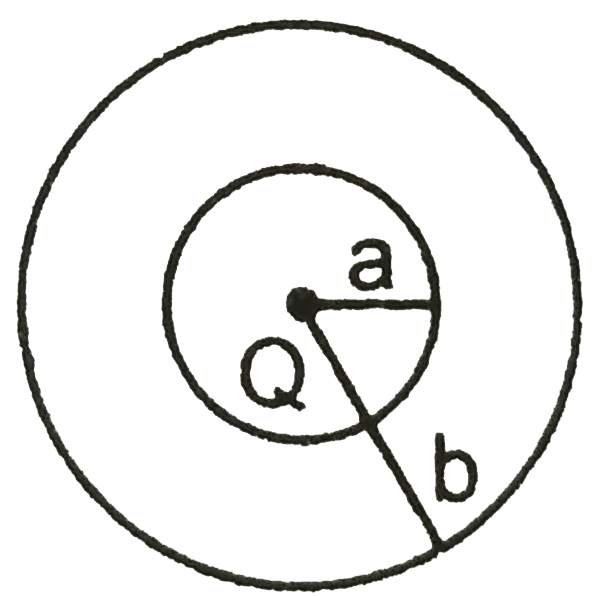
View Solutionमान गोलाथ सम्मित आवेश वितरण में आवेश घनत्व r=R तक `rho(r)=rho_(0)(5/4-(r )/(R ))` के अनुसार बदलता है तथा `rgtR` तक `rho(r )=0` बदलता है जहाँ r मूल बिंदु से दुरी है मूल बिंदु से `r(rltR)` दुरी पर विधुत क्षेत्र है
View Solutionएक बिंदु आवेश Q एक एकसमान रेखाइये आवेश घनत्व `lambda` वाले अनंत लम्बाई के तार तथा एक एकसमान षेरेस्ट आवेश घनत्व `sigma` वाले अन्ननत समतल चादर के कारण r दुरी पर विधुत क्षेत्र की त्रिवताये क्रमश `E_(1)(r ),E_(2)(r )` तथा `E_(3)(r )` है यदि एक दी गयी दुरी `r_(0)` पर `E_(1)(r_(0))=E_(2)(r_(0))=E_(3)(r_(0))` तब
View Solution
वस्तुनिष्ठ प्रकार प्रशन questions and complete solutions for chapter वैधुत फ्लेक्स तथा गौस की प्रमेय of NAGEEN PHYSICS (HINDI) of Class 12