Complete Solutions to Partice Exercise of chapter ELECTROSTATICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTROSTATICS |
| PHYSICS GALAXY | Partice Exercise |
| Number Of Questions | 93 |
| Academic Year | 2023-24 |
Two positively charged small particles, each of mass `1.7 xx 10^(-27) kg` and carrying a charge of `1.6 xx 10^(-19) C` are placed apart at a separation r. If each one experiences a repulsive force equal to its weight find their separation. [0.117 m]
View SolutionTwo particles (free to move) with charges `+q` and `+4q` are a distance L apart. A third charge is placed so that the entire system is in equilibrium.
(a) Find the location, magnitude and sign of the third charge.
(b) Show that the equilibrium is unstable.
View SolutionA charge Q is to be divided on two objects. What shouold. be the values of the charges on the objects so that the. force between the objects can be maximum?.
View SolutionThree charges `q_(1), q_(2)` and `q_(3)` are shown in figure . Determine the net force acting on charge `q_(1)` . The charges and separation are given as ` q_(1) =- 1.0 xx 10^(-6)C, q_(2) =+ 3.0 xx 10^(-6)C`, and `q_(3) = - 2.0 xx 10^(-6)C, r_(12) = 15 cm, r_(13) = 10 cm` and `theta = 30^(@)`.

View SolutionThree Charges of magnitude `100 muC` are placed at the corners A, Band C ofan equilateral triangle of side 4m. If the charge at A and Care positive and the one at point B is negative, what is the magnitude and direction of total force acting on charge at C? `[5.625N]`
View SolutionTwo negative charges of a unit magnitude and a positive charge q are placed along a straight line. At what position and value of q will the system be in equilibrium? (Negative charges are fixed).
View SolutionA charges Q is placed at each of the two opposite corners of a square. A charge q is placed to each of the other two corners. If the resultant force on each charge q is zero, then
View SolutionTwo balls of the same radius and weight are suspended on threads so that their surface are in contact. A charge of `q_(0) = 4 xx 10^(-7)C` is given to the balls which makes them repel each other and diverge to an angle of `60°`. Find the mass of the balls if the distance of balls from the point of suspension to the centre of ball is 20cm. Find the density of the material of the balls if the angle of divergence becomes `54°` when the balls are immersed in kerosene of density `800kg m^(-3)` dielectric constant ofkerosene is `epsilon_(r) = 2 [1.592g, 255 K//g m^(3)]`
View SolutionTwo equal positive point charges are separated by a distance 2a. A point test charge is located in a plane which is normal to the line joining these charges and midway between them.
(a) Calculate the radius r of the circle of symmetry in this plane for which the force on the test charge has a maximum value.
(b) What is the direction of this force, assuming a positive test charge ? [at `sqrt(2)`, radial and away from the center]
View SolutionConsider a fixed charge Q and another charge q is placed at a distance `x_(0)` from Q on a smooth plane surface. Find the velocity of charge q as a function of x.
`[[(Qq)/(2pi in_(0)m){(1)/(x_(0))-(1)/(x)}]^(1/2)]`
View SolutionA positive point charge `50mu C` is located in the plane xy at a point with radius vector `vecr_(0)=2hat(i)+3hat(j)`. The electric field vector `vec(E )` at a point with radius vector `vec(r )=8 hat(i)-5 hat(j)`, where `r_(0)` and r are expressed in meter, is
View SolutionFour point charges, each of `+q`, are rigidly fixed at the four corners of a square planar soap film of side 'a'. The surface tension of the soap film is `gamma`. The system of charges and planar film are in equilibrium, and `a=k[(q^2)/(gamma)]^(1//N)`, where 'K' is a constant. Then N is
View SolutionTwo identical beads each have a mass m and charge q. When placed in a hemispherical bowl of radius R with frictionless, non-conducting walls, the beads move, and at equilibrium they area distance R apart (figure). Determine the charge on each bead.
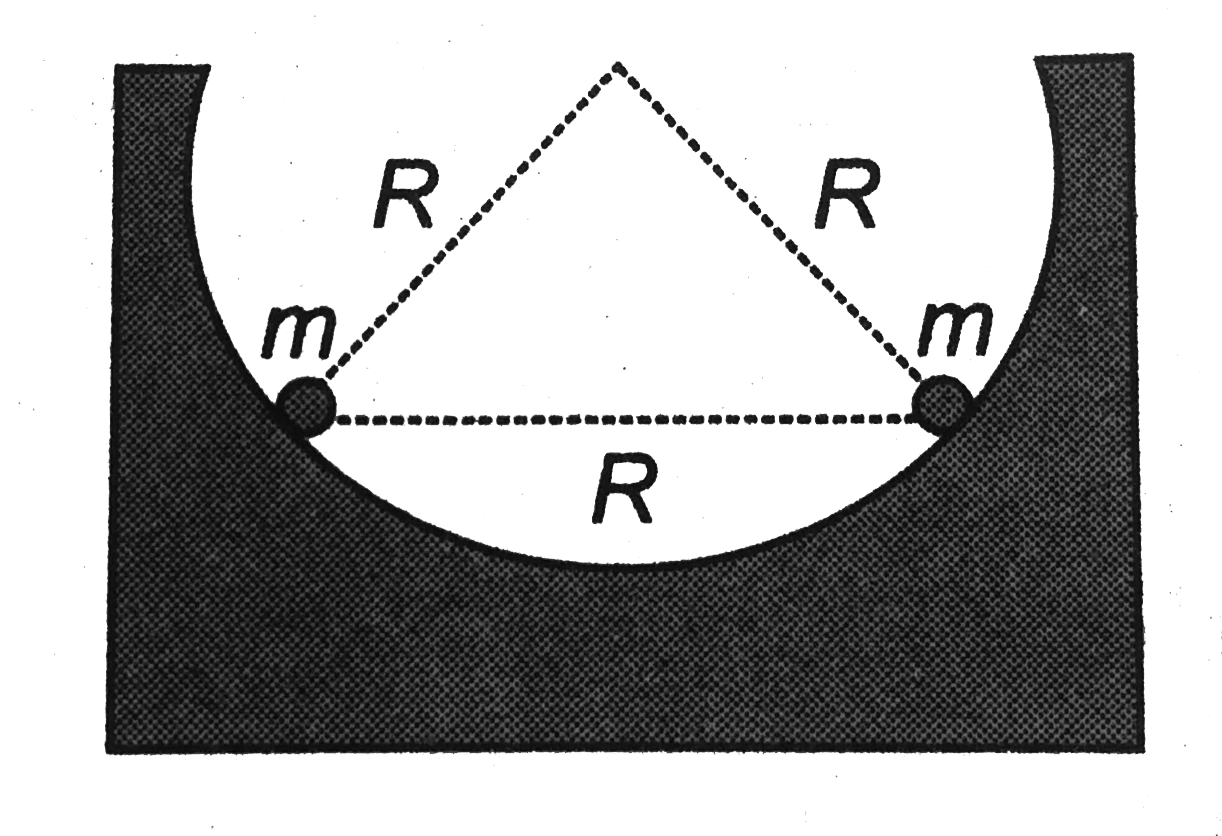
View SolutionTwo horizontal parallel conducting plates are kept at a separation `d = 1.5 xx 10^(-2) m` apart one above the other in air as shown in figure. The upper plate is maintained at a positive potential of `1.5 kV`while the other plate is earthed which maintains it at zero potential. Calculate the number of electrons which must be attached to a small oil drop of mass `m =4.9 xx 10^(-15) kg` between the plates to maintain it at rest. Consider density of air is negligible in comparison with that ofoil. If the potential of above plate is suddenly changed to `-l .5kV`, what will be the initial acceleration of the charged drop? Also calculate the terminal velocity of the drop if its radius is `r= 5.0 xx 10^(-6)m` and the coefficient of viscosity of air is `eta = 1.8 x 10--5 N-s//m^(2) [3,2g, 5.7 xx 10^(-5) m//s^(2)]`

View SolutionA uniform electric field of intensity `E = 10^(6) V//m` exist in vertically downwards direction in a region. A particle of mass m = 0.01 kg andcharge `q= 10^(-6) C` is suspended byan inextensible thread oflength `I= 1m`. The particle is displaced slightly from its mean position and released. Calculate the time period ofits oscillation. What minimum velocity should be given to the particle at rest from its equilibrium position so that it completes a full circle in vertical plane? Calculate the maximum and minimum tension in the thread in its circular motion in vertical plane. `[0.6s, 23.42 m//s, 6.59 N,0]`
View SolutionFigure shows an assembly of deflecting plates A and B ofan ink-jet printer which causes moving ink droplets to deflect at desired displacements by continuously varying electric field between the plates. An ink drop with a mass `m = 1.3 xx 10^(-10)kg` and a negative charge of magnitude `q = 1.5x x 10^(-13)C` enters the region between the plates, initially moving along the x-axis with speed `v_(x), = 18m//s`. The length of plates is `L = 1.6cm`. The plates are connected with a varying voltage and thus produce an electric field at all points between them. Assume that field `vec(E)` for some duration is constant and it is acting in downward direction as shown and has a magnitude of `E = I .4 xx 10^(6) N//C`, find the vertical deflection of the drop at the far edge ofthe plate? As the gravitational force on the drop is very small relative to the electrostatic force acting on the drop, it can be neglected for this analysis. `[6.4 xx 10^(-4)m]`

View SolutionA uniform electric field E is established between two parallel charged plates as shown in figure. An electron enter the field symmetrically between the plates with a speed u. The length of each plate is l. if the electron does not stricke any of the plates, find the angle of deviation of the electron as it comes out of the field at the outer end of plates. `[tan^(-1) ((eEl)/(mu^(2)))]`

View SolutionIn a region an electric field is setu!l with its strength `E = 15 N//C` and it makes an angle of `30°` with the horizontal plane as shown in figure. A ball having a charge 2C, mass 3kg and coefficient of restitution with ground 0.5 is projected at an angle of `30°` with the horizontal along the direction of electric field with speed 20 m/s. Find the horizontal distance travelled by ball from first hit with the ground to the second time when it hits the ground. `[70 sqrt(3)m]`

View SolutionIn a hydrogen atom an electron of mass `9.1 xx 10^(-31) jg` revolves about a proton in circular orbit of radius `0.53 Å`. Calculate the radial acceleration and angular velocity of electron. `[8.9 xx 10^(22) m//s^(2), 4.1 xx 10^(16)s^(-1)]`
View SolutionAn electron is released with a velocity of `5xx10^(6)ms^(-1)` in an electric field of `10^(3)NC^(-1)` which has been applied so as to oppose its motion. What distance would the electron travel and how much time could it take before it is brought to rest?
View SolutionA particle is unchanged and is thrown vertically upward from ground level with a speed of `5sqrt(5)` m//s in a region of space having uniform electric field As a result, it attains a maximum height h. The particle is then given a positive charge +q and reaches the same maximum height h when thrown vertically upward with a speed of `13 m//s` Finally the particle is given a negative charge -q Ignoring air resistance determine the speed (in m//s) with which the negatively charged particle must be thrown vertically upward, so that it attains exactly the same maximum height h.
View SolutionA particle of charge q and mass m is suspended from a point on the wall by a rigid massless rod oflength `L = 3//m` as shown. Above the point of suspension another particle is clamped which has a charge -q at a distance L .from point of suspension. On slight displacement from the mean position, the suspended particle is observed to executes SHM. Find the time period of SHM. (For calculations consider `Kq^(2) = 2mgL^(2) `and `g = pi^(2)) [4s]`
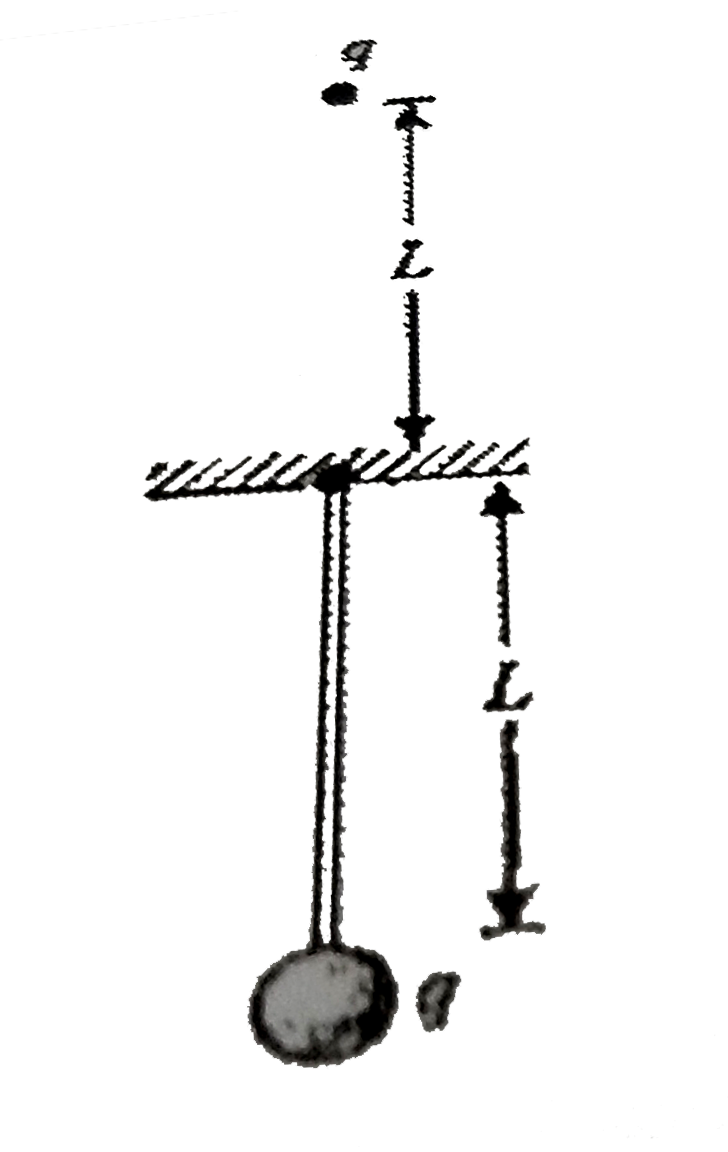
View SolutionA nonconducting ring of mass m and radius R, with charge per unit length `lambda` is shown in fig. It is then placed on a rough nonconducting horizontal plane. At time t=0, a uniform electric field `vecE =E_(0)hati` is switched on and the ring starts rolling without sliding. Determine the friction force (magnitude and direction ) acting on the ring.

View SolutionIn the given arrangement find electric field at C. Complete wire is uniformly charged at linear charge density `lambda. [(lambda)/(2sqrt(2)in_(0)R)]`
View SolutionA thin half ring of radius `R = 20 cm` is uniformly charged with a total charge `q = 0.70 nC`.Find the magnitude of the electric field strength at the curvaite centre of this half-ring.
View SolutionThree short electric dipoles, each of dipole moment P, are placed at the vertices of an equilateral triangle of side length L. Each dipole has its moment oriented parallel to the opposite side of the triangle as shown in the fig. Find the electric field and potential at the centroid of the triangle
View SolutionA whin wire ring of radius `r` carries charge `q`. Find the magnitude of the electric field strength on the axis of the ring as a function of distance `l` from its centre. Investigate the obtained function at `l gt gt r`. Find the maximum strength magnitude and the corresponding distance `l`. Draw the appoximate polt of the function. `E (l)`.
View SolutionA circular wire-loop of radius a carries a total charge Q distributed uniformly over its length . A small length dL of the wire is cut off. Find the electric field at the centre due to remaining wire.
View SolutionAn electron is constrained to move along the central axis of a ring ofradius R having uniformly distributed charge q. Show that the electrostatic force exerted on the electron can cause itto oscillate through the centre of the ring with an angular frequency of `omega = sqrt((eq//4pi epsilon_(0)mR^(3)))`, where m is the mass of the electron `[sqrt((qe)/(4pi in_(0)mR^(3)))]`
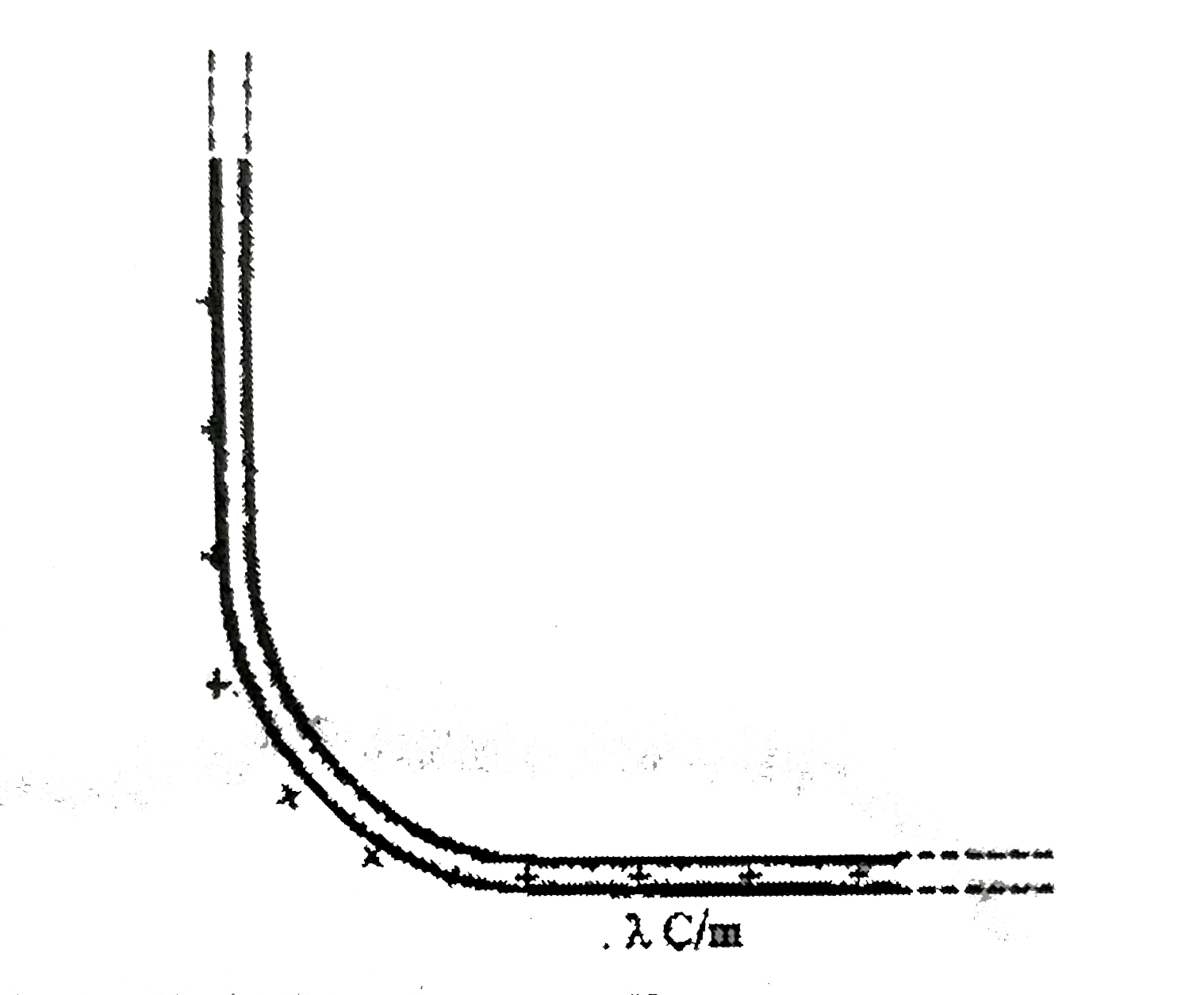
View SolutionTwo point charges `Q_(1)` and `Q_(2)` are positioned at points I and 2. The field intensity to the right of the charge `Q_(2)` on the line that passes through the two charges varies according to a law that is represented in the figure. The field intensity is assumed to be positive if its direction coincides with the positive direction on the x-axis. The distance between the charges is l.
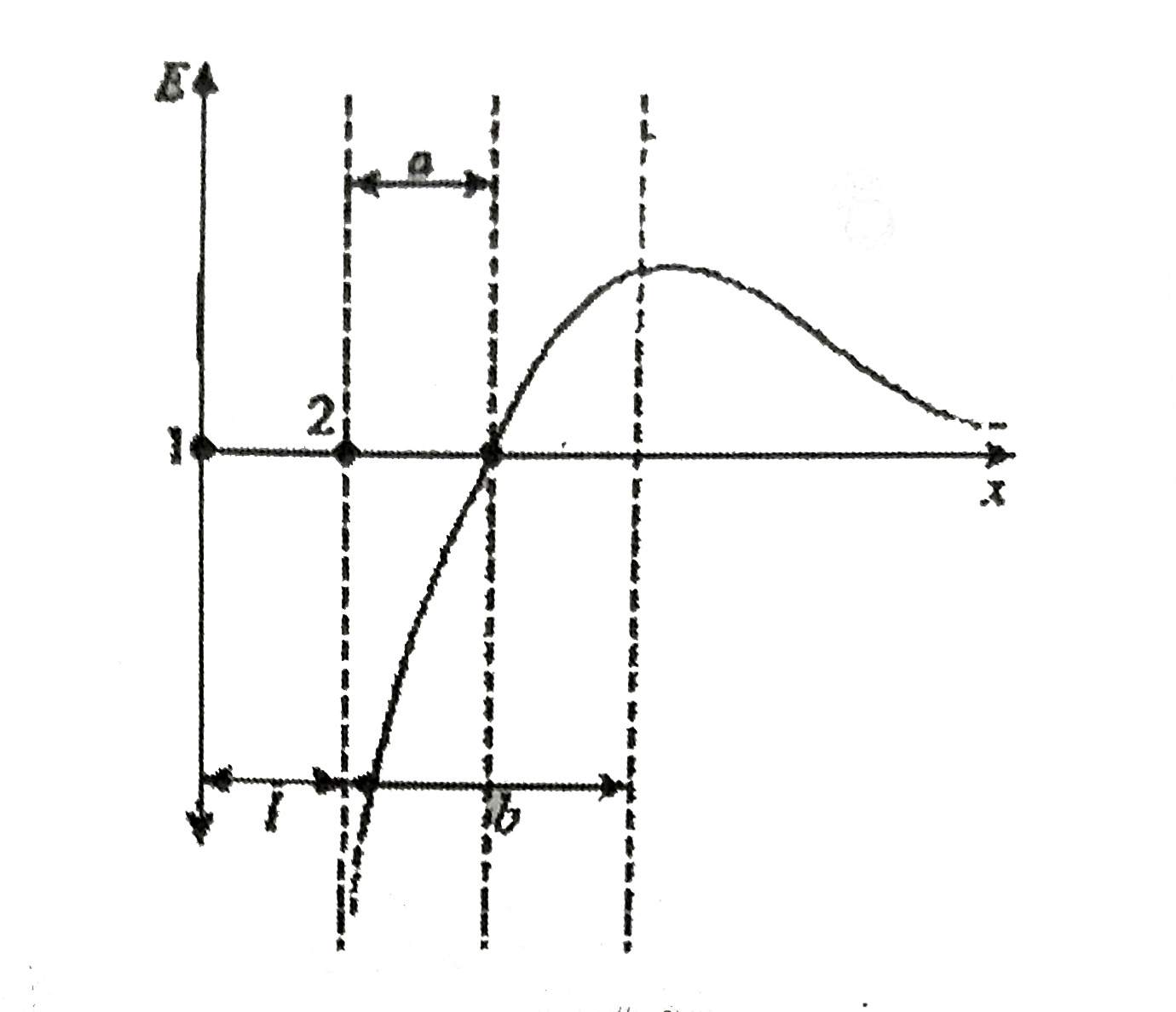
(a) Find the sign of each charge
(b) Find the ratio of the absolute values of the charges `|(Q_(1))/(Q_(2))|`
(c) Find the value of b where the field intensity is maximum
[(a) `Q_(2)` is negative and `Q_(1)` is positive (b) `((l +a)/(a))^(2)`, (c) `(l)/(((l+a)/(a))^(2//3)-1)]`
View SolutionTwo wires AB & CD, each `1m` length, carry a total charge of `0.2` microcoulomb each and are placed as shown in figure. The ends B & C are separated 1 m distance. Determine the value of electric intensity at the point P in the vector form.Note P is the mid point of BC.
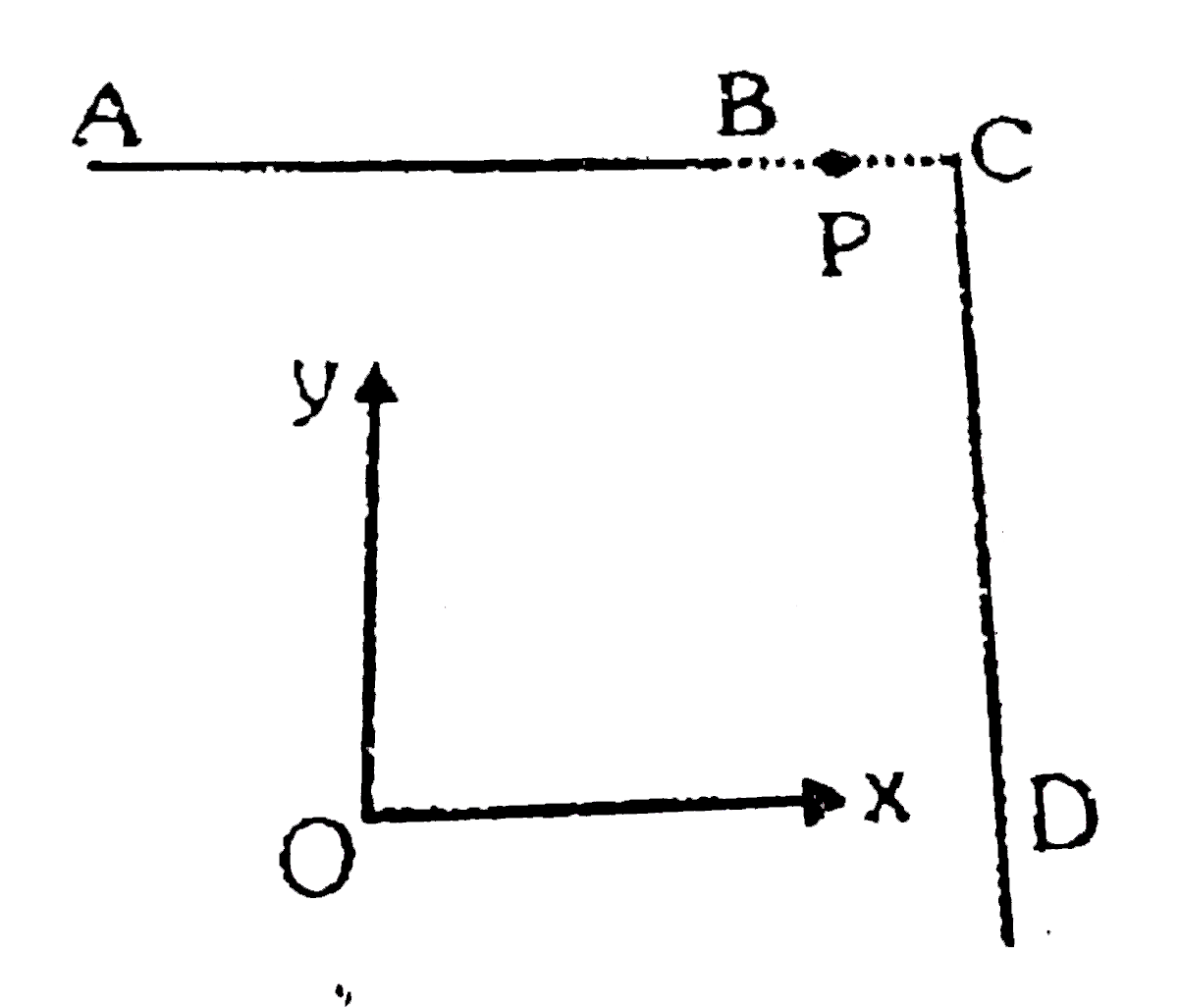
View SolutionThe diagram shows a uniformly charged hemisphere of radius R. It has volume charge density rho. If the electric field at a point 2R distance above its center is E then what is the electric field at the point which is 2R below its center?

View SolutionAn infinitely long solid cylinder of radius ` R` has a uniform volume charge density `rho`. It has a spherical cavity of radius `R//2` with its centre on the axis of cylinder, as shown in the figure. The magnitude of the electric field at the point `P`, which is at a distance `2 R` form the axis of the cylinder, is given by the expression `( 23 r R)/( 16 k e_0)` . The value of `k` is .
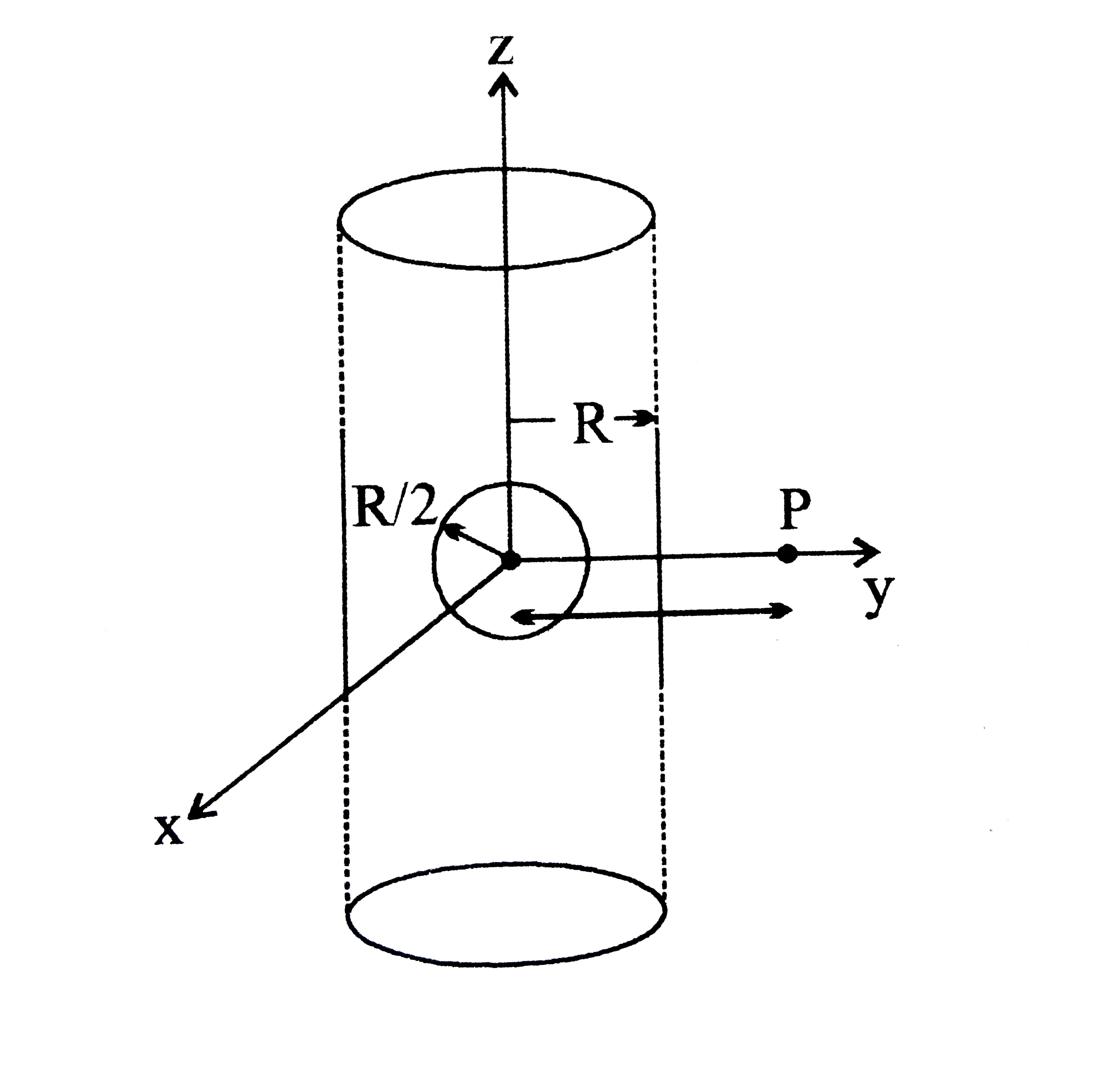 .
.
View SolutionThere are two nonconducting spheres having uniform volume charge densities `rho` and `- rho` . Both spheres have equal radius `R`. The spheres are now laid down such that they overlap as shown in Fig.2.125. Take `vec(d) = O_(1) vec(O_(2))`.

The electric field `vec(E)` in the overlapped region is
View SolutionSuppose the surface charge density over a sphere of radius R depends on a polar angle `theta` as `sigma = sigma_(0)cos theta`, where `sigma_(0)` is a positive constant. Show that such a charge distribution can be represented ~s a result ofa small relative shift of two uniformly · charged balls of radius R whose charges are equal in magnitude and opposite in sign. Resorting to this representation, find the electric field strength vector inside the given sphere. `[(sigma_(0))/(3in_(0))]`
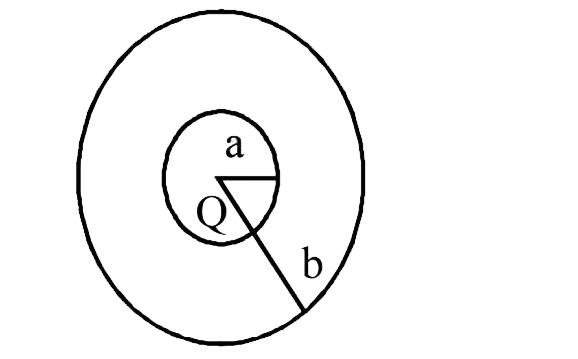
View SolutionThe region between two concentric spheres of radii 'a' and 'b', respectively (see figure), have volume charge density `rho=A/r`, where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant, is:
View SolutionA square loop of side 'l' each side having uniform linear charge density 'lambda' is placed in 'xy' lane as shown in the figure There exists a non uniform electric field `vec(E)=a/l(x+l)hat(i)` where a and l are constants and x is the position of the point from origin along x-axis. Find the resultant electric force on the loop (in Newtons) if `l=10 cm lambda=20 muC//m and a=5 xx 10^(5) N//C`.

View SolutionTwo concentric rings, one of radius a and the other of radius b, have the charges +q, and `-(2//5)^(-3//2)q`, respectively as shown in fig.
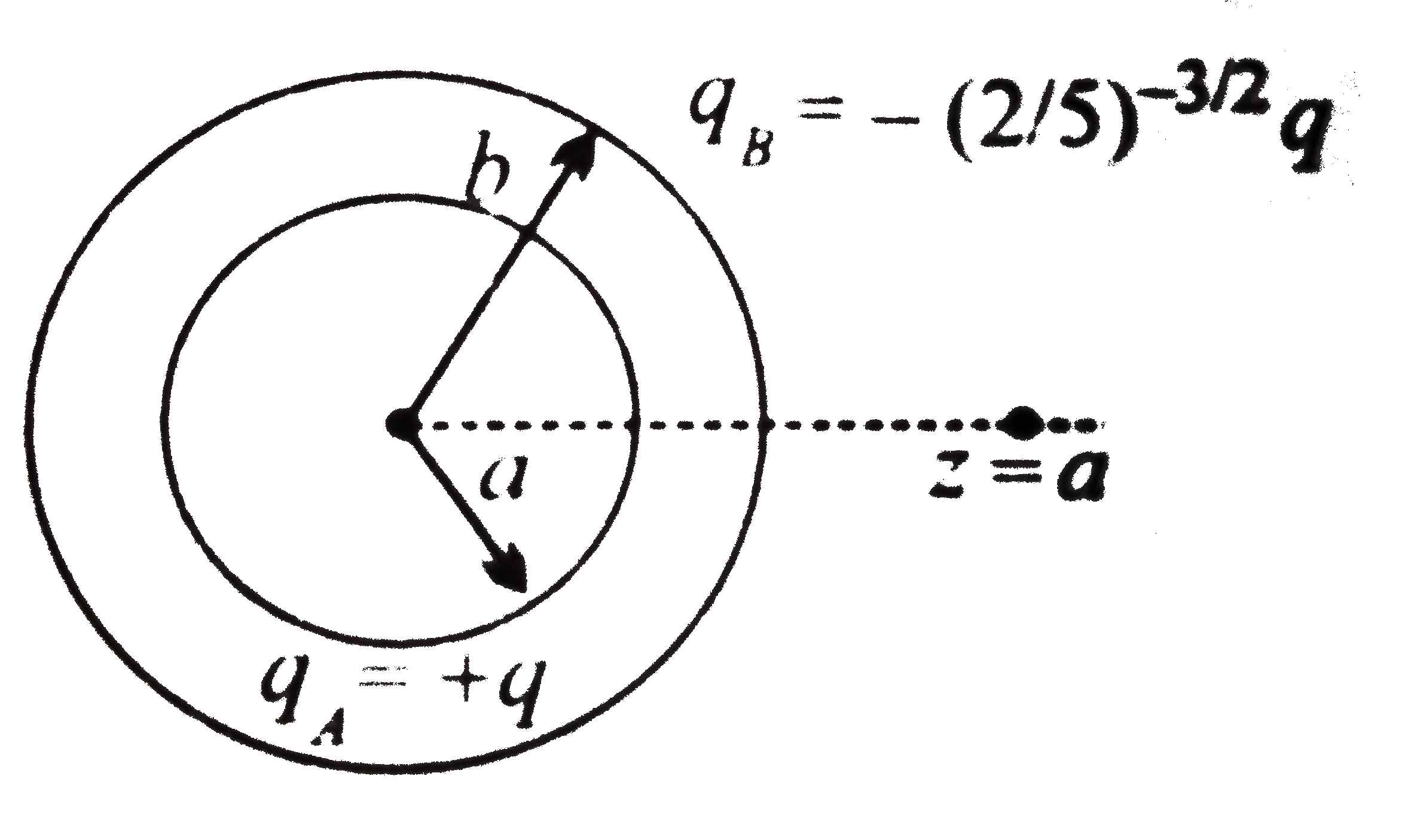
Find the rario `b//a` if a charge particle palaced on the axis at z =a is i equilibrium.
View SolutionAn infinite dielectric sheet having charge density `sigma` has a hole of radius R in it. An electron is released from point P on the axis of the hole at a distance `sqrt(3)R` from the center. Find the speed with which it crosses the plane of the sheet.
 .
.
View SolutionA uniform rod AB of mass m and length `l` is hinged at its mid point C. The left half (AC) of the rod has linear charge density `-lamda` and the right half (CB) has `+ lamda` where `lamda` is constant. A large non conducting sheet of uniform surface charge density `sigma` is also present near the rod. Initially the rod is kept perpendicular to the sheet. The end A of the rod is initialy at a distance d. Now the rod is rotated by a small angle in the plane of the paper and released. Prove that the rod will perform SHM and find its time period.

View SolutionTwo particles each charged with a charge +q are clamped on they axis at the points (0, a) and (0, - a). If a positively charged particle of charge `q_(0)` and mass m is slightly displaced from origin in the direction ofnegativex-axis.
(a) What will be its speed at infinity?
(b) If the particle is projected towards the left along the x-axis from a point at a large distance on the right of the origin with a velocity half that acquired in part (a), at what distance from origin will it come to rest ?
`[sqrt((2Kqq_(0))/(ma)),sqrt(15)a]`
View SolutionAn infinite number of charges each equal to q are placed along the x-axis at `x= 1m,x=2m,x=4m,x=8m`, ... and so on. Find the potential and electric field at the point x = 0 due to this set of charges. What will be potential and electric field ifin the above set up if the consecutive charge have opposite sign?
`[(q)/(2pi in_(0)),(q)/(3pi in_(0)), (q)/(6pi in_(0)),(q)/(5pi in_(0))]`
View SolutionA particle having a charge of `1.6 x 10^(-19) C` enters midway between the two plates of a parallel plate capacitor. The initial velocity of particle is parallel to the plates. A potential difference of300 Vis applied between the two plates. lfthe length of the plates is 10 cm and they are separated by 2 cm, calculate the greatest initial velocity for which the particle will not be able to come out of the plates. The mass of the particle is `12 xx 10^(-24) kg`
`[10^(4) m//s]`
View SolutionA circular ring of radius R with uniform positive charge density `lambda` per unit length is located in the y-z plane with its centre at the origin O. A particle of mass m and positive charge q is projected from the point P `(Rsqrt3, 0, 0)` on the positive x-axis directly towards O, with an initial speed v. Find the smallest (non-zero) value of the speed v such that the particle does not return to P.
View SolutionTwo thin wire rings each having radius R are placed at distance d apart with their axes coinciding. The charges on the two are `+Q` and `-Q`. The potential difference between the centre so the two rings is
View SolutionA positive charge Q is uniformly distributed throughout the volume of a dielectric sphere of radius R. A point mass having charge +q and mass m is fired toward the center of the sphere with velocity v from a point at distance `r (r gt R)` from the center of the sphere. Find the minimum velocity v so that it can penetrate `(R//2)` distance of the sphere. Neglect any resistance other than electric interaction. Charge on the small mass remains constant throughout the motion.

View SolutionThe electric potential at surface of thin non-conducting sheet with charge density `sigma` is `V_(0)`. Show that the electric potential at a distance x from infinite sheet can be written as
`V = V_(0) - (sigma)/(2 in_(0)) x`
View SolutionTwo identical circular rings A and B of radius 30 cm are placed coaxially with their axes horizontal in a uniform electric field `E. = 10^(5)N//C` directed vertically upward as shown in figure. Distance between centres ofthese rings A and B is40cm. Ring A has a positive charge `10muC` while ring B has a negative charge of magnitude `20muC`. A particle of mass `100g` and carrying a positive charge `10muC` is released from rest at the centre of the ring A. Calculate its velocity when it has moved a distanceof40cm. Take `g= 10m//s^(2)`
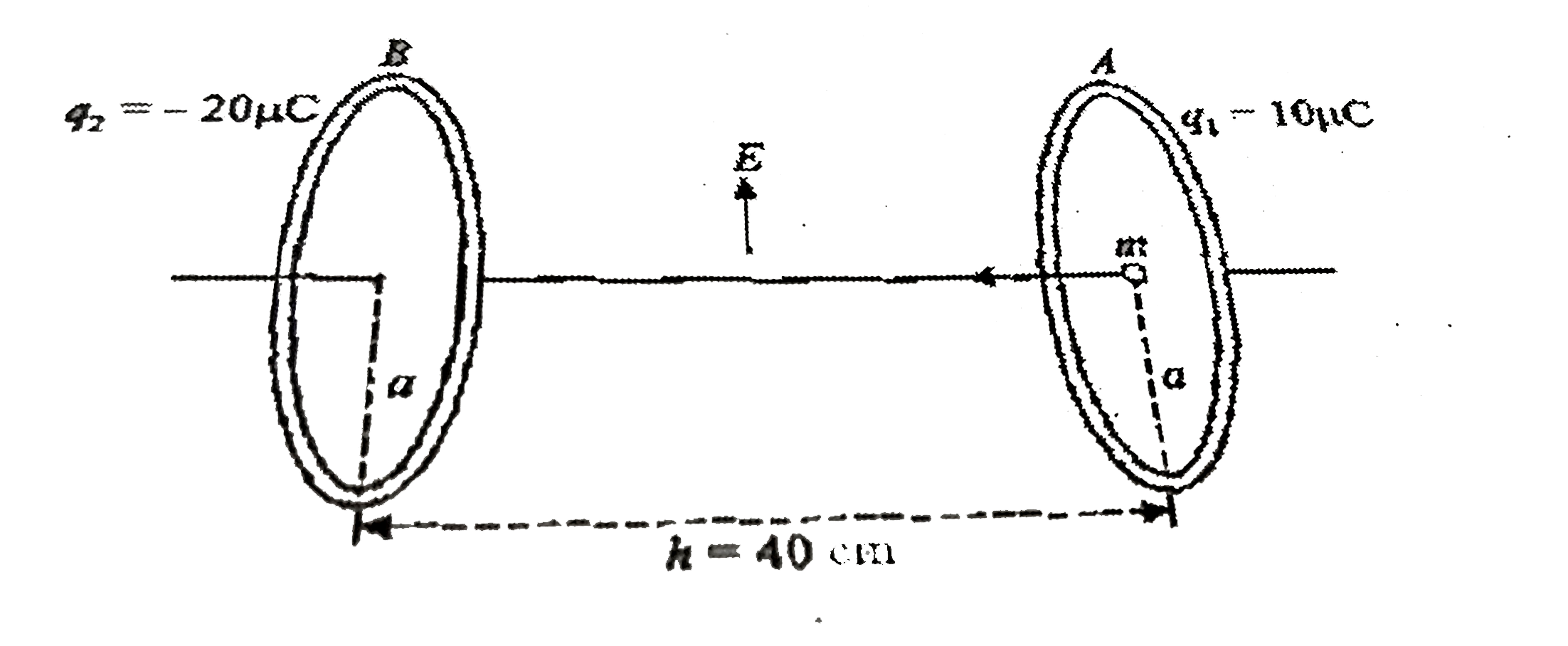
`[6 sqrt(2) m//s]`
View SolutionA non-conducting disc of radius a and uniform positive surface charge density `sigma` is placed on the ground, with its axis vertical. A particle of mass m and positive charge q is dropped, along the axis of the disc, from a height H with zero initial velocity. The particle has `q//m=4 in_0 g//sigma`
(a) Find the value of H if the particle just reaches the disc.
(b) Sketch the potential energy of the particle as a function of its height and find its equilibrium position.
View SolutionDetermine the potential `phi (x,y,z)` of an electrostatic field `vec(E) = ay hati + (ax + bz) hatj + by hatk`, where a and b are constants, `hati, hatj` are the unit vectors of the axes x,y,z. `[-y(ax +bz)+` constant]
View SolutionFind the potential difference between points a and b in and electric field of which strength in the region is given by the vector as
`vec(E) = (2hati + 3hatj + 4 hatk) N//C`
The position vectors of points a and b are given as
`vec(r)_(a) = (hati - 2hatj +hatk)m` and `vec(r)_(b) = (2hati +hatj - 2hatjk)m [-1V]`
View SolutionConsider a spherical surface of radius 4 m cenred at the origin. Point charges +q and - 2q are fixed at points A( 2 m, 0,0) and B( 8 m, 0, 0), respectively. Show that every point on the shperical surface is at zero potential.
View SolutionA plastic rod has been formed into a circle of radius R. It has a positive charge `+Q` uniformly distributed along one-quarter of its circumference and a negative charge of ` -6Q` uniformly distributed along the rest of the circumference (figure). With V = 0 at infinity, what is the electric potential `-6Q`
(a) at the centre C of the circle and
(b) at point P, which is on the central axis of the circle at distance z from the centre?
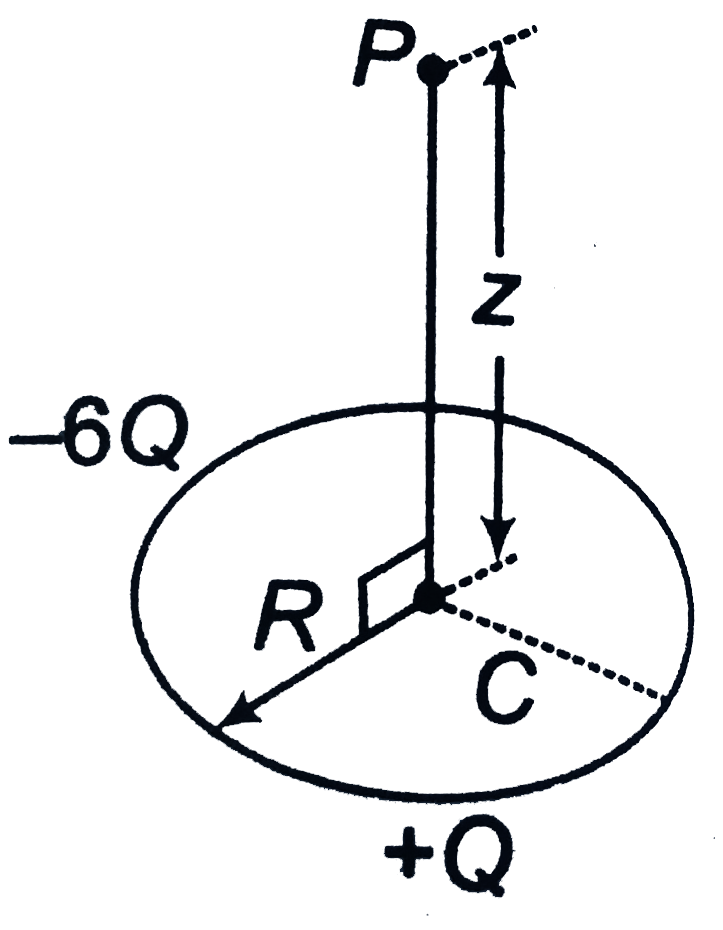
View SolutionA ring of radius R is having two charges `q` and `2q` distributed on its two half parts. The electric potentiasl at a point on its axis at a distance of `2sqrt2 R` from its centre is `(k=1/(4piepsilon_0))`
View SolutionA spherical oil drop, radius `10^(-4)` cm has on it at a certain a total charge of 40 electrons. Calculate the energy that would be required to place an additional electron on the drop.
View SolutionThree charges ` 0.1` coulomb each are placed on the corners of an equilateral triangle of side `1 m`. If the energy is supplied to this system at the rate of ` 1 kW` how much time would be required to move one to the charges on to the midpoint of the line joining the two ?
View SolutionA system consists of two concentric spheres, with the inside sphere of radius a carrying a positive charge `q_(1)`. What charge `q_(2)` has to be diposited on the outsie sphere of radius `b` to reduce the potentail `varphi` depend in this case on a distance `r` from the centre of the system ? Draw teh appoximate plot of this dependence.
View SolutionAt the end points of a line sigment of a length of `d = (sqrt(337))/(84)m` there are two identical positive electric charges q. What is the ratio of the electric field strength and the electric potential magnitudes is SI units at a point located by an angle `a = 37^(@)` on the circle drawn around the line segment as a diameter?

View SolutionA conducting sphere `S_1` of radius `r` is attached to an insulating handle. Another conduction sphere `S_2` of radius `R` is mounted on an insulating stand. `S_2` is initially uncharged. `S_1` is given a charge `Q` brought into contact with `S_2` and removed. `S_1` is recharge such that the charge on it is again `Q` and it is again brought into contact with `S_2` and removed. This procedure is repeated `n` times.
a. Find the electrostatic energy of `S_2` after `n` such contacts with `S_1`.
b. What is the limiting value of this energy as `nrarroo` ?
View SolutionA uniform disc of radius R is charged with a uniform surface charge density `sigma`. Find the electric potential due to the charges on the disc at a point on its edge. `[(sigmaR)/(piin_(0))]`
View SolutionA dielectric cylinder of radius a is infinitely long. It is non-uniformly charged such that volume charge density `rho` varies directly as the distance from the cylinder. Calculate the electric field intensity due to it at a point located at a distance r from the axis of the cylinder. Given that `rho` is zero at the axis and it is equal to `rho` on the surface of cylinder. Also calculate the potential difference between the axis and the surface. `[(rhor^(2))/(3in_(0)a),(rhoa^(2))/(9in_(0))]`
View SolutionIn figure-, an electric dipole is placed at a distance x from an infinitely long rod of linear charge density `lambda`.
(a) Find the net force acting on the dipole
(b) What is the work done in rotating the dipole through `180^(@)`
(c ) If the dipole is slightly rotated about its equilibrium position, find the time period of oscillation. Assume that the dipole is linearly restrained.
`[(a)(lambdaaq)/(piin_(0)x^(2)),(b) (2lambdaaq)/(piin_(0)x),(c ) 2pisqrt((2piin_(0)mx^(2)a)/(lambdaq))]`

View SolutionTwo point dipoles `phat(k)` and `(P)/(2) hat(k)` are located at (0, 0, 0) and (1m, 0, 2m) respectively. Find the resultant electric field due to the two dipoles at the point M(1m, 0, 0)
`[-((7P)/(32piin_(0)))hat(k)]`
View SolutionFind the magnitude of the electric field at the point P in the configuration shown in figure- 1.219 (a), (b) and (c ) for `d gtgt a` take 2qa=P.
`[(a)(q)/(4piin_(0)d^(2)),(b)(2q)/(2piin_(0)d^(3)),(c ) (q)/(4piin_(0)d^(2))sqrt(1+(4a^(2))/(d^(2)))]`

View SolutionThe graph in figure-shows the potential energy of an electric dipole that oscillates between `pm 60^(@)`. What is the kinetic energy of dipole when it is aligned with the field?
`[1muJ]`

View SolutionAn electric dipole with dipole moment P oriented in the positive direction of z-axis is located at the origin of a three dimensional coordinate system. Find the projections of electric field `E_(x)` and `E_(y)` of the electric field strength vector at a point `P(r, theta)`. Aslo find out the angle `theta` at which electric field vector is perpendicular to the dipole moment.
`[(P)/(4piin_(0)r^(3))(3cos^(3)theta-1),(3p sinthetacostheta)/(4piin_(0)r^(3)),cos^(-1)((1)/(sqrt(3)))]`

View SolutionAn electric dipole is placed at a distance x from centre O on the axis of a charged ring of radius R and charge Q uniformly distributed over it.
(a) Find the net force acting on the dipole
(b) What is the work done in rotating the dipole through `180^(@)`?
`[(a) (aqQ)/(2piepsilon_(0))((R^(2)-2x^(2))/((R^(2)+x^(2))^(3//2))), (b) (aqQx)/(piepsilon_(0)(R^(2)+x^(2))^(3//2))]`

View SolutionA dipole with an electric moment p is located at a distance r from a along thread charge uniformly with a linear density `lambda`. Find the force F acting on the dipole if the vector p is oriented
(a) along the thread
(b) along the radius vector r
(c ) at the right angles to the thread and the radius vector r.
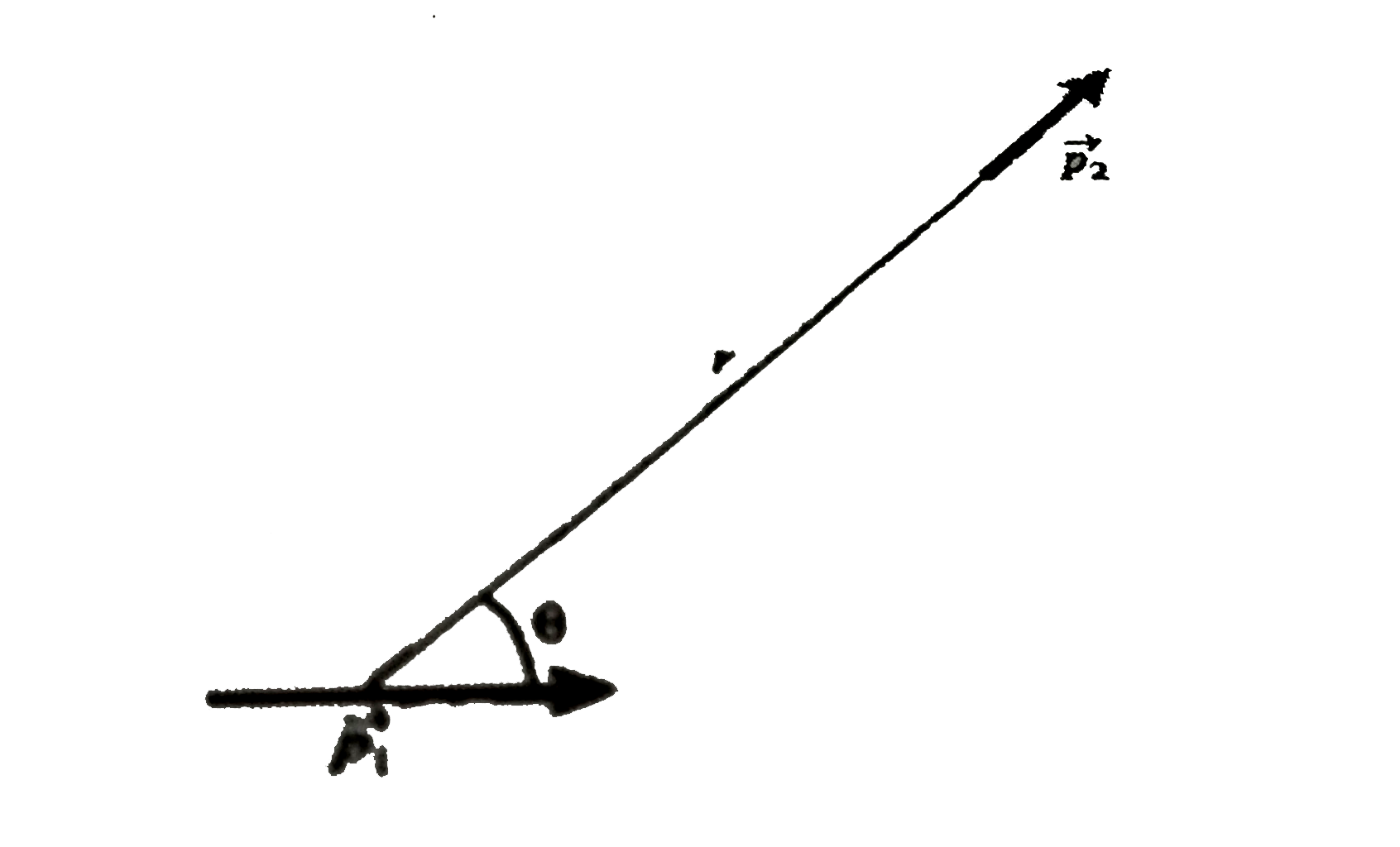
View SolutionTwo short electric dipoles are placed as shown in figure. Find the potential energy of electric interaction between these dipoles.
`[-(Kp_(1)p_(2)costheta)/(r^(3))]`
View SolutionIn the figure shown S is a large nonconducting sheet of uniform charge density `sigma`. A rod R of length l and mass 'm' is parallel to the sheet and hinged at its point. The linear charge densities on the upper and lower half of the rod are shown in the figure. Find the angular acceleration of the rod just after it is released
`[(3sigmalambda)/(2m in_(0))]`
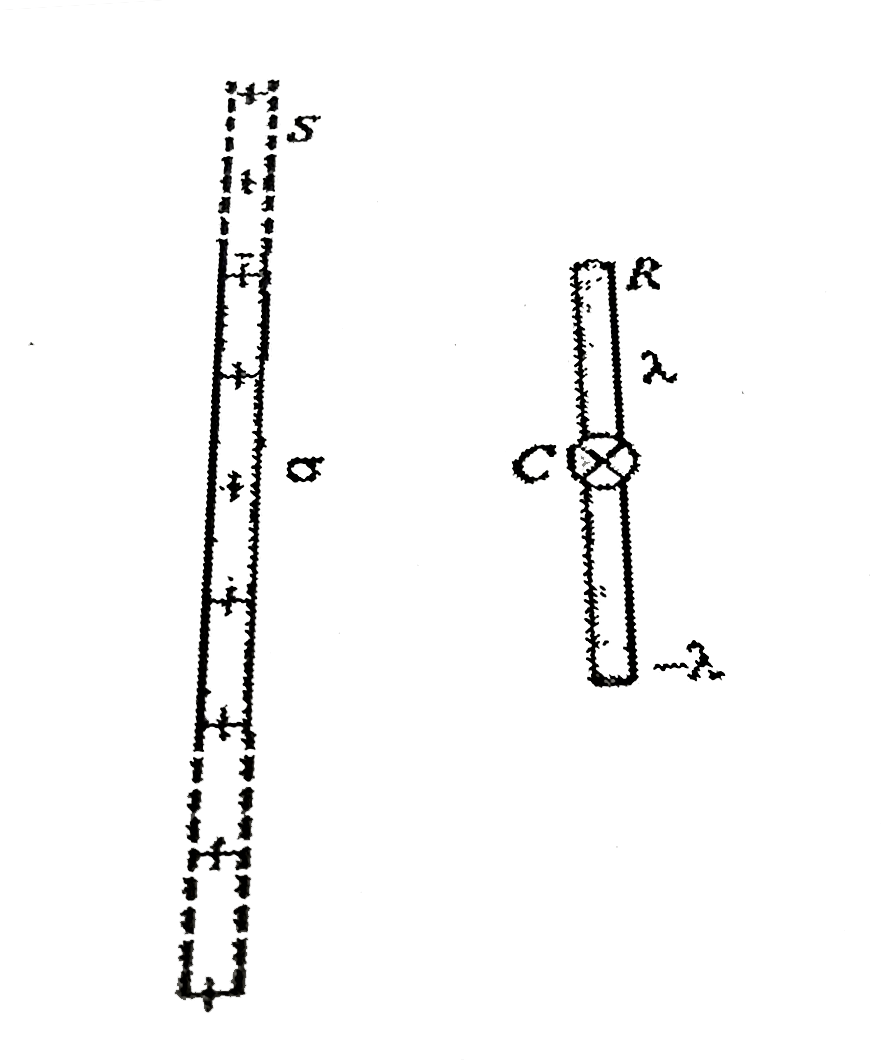
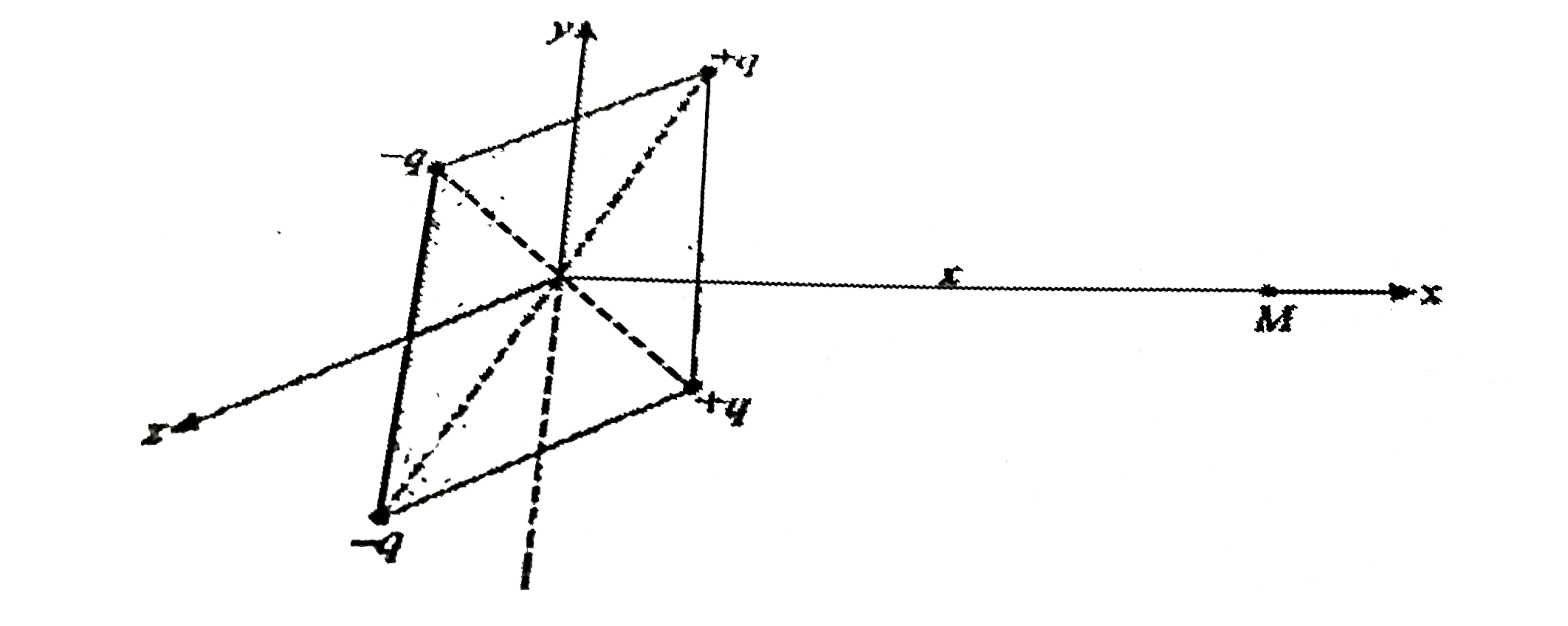
View SolutionPoint charges q and -q located at the vertices of a square with diagonals 2l as shown in figure. Find the magnitude of the electric field at a point located symmetrically with respect to the vertices of the square at a distance x from its centre. Consider `x gtgt l_(0)`
`[-(ql)/(sqrt(2)piepsilon_(0)x^(3))]`
View SolutionTwo point charges `q` and `-q` are separated by a distance `2l`. Find the flux strength vector across the circle of radius R placed with its centre coinciding with the of line joining the two charges in the perpendicular plane.
View SolutionA charge `q_0` is distributed uniformly on a ring of radius R. A sphere of equal radius R constructed with its centre on the circumference of the ring. Find the electric flux through the surface of the sphere.
View SolutionAn electric field given by `vec(E)=4hat(i)+3(y^(2)+2) hat(j)` pierces a gaussian cube of side 1m placed at origin such that one of its corners is at origin and rest of sides are along positive side of coordinate axis. Find the magnitude of net charge enclosed within the cube
`[3 in_(0)]`
View SolutionA point charge q is located on the axis of a disc of radius R at a distance b from the plane of the disc as shown in figure 1.295 What should be the radius of the disc if one fourth of the total electric flux form the charge passes through the disc.

View SolutionFind the electric flux through a cubical surface due to a point charge q placed (a) at centre of one face (b) corner of the cubical box as shown in figures -1.296 below in case (b) find the flux through each face of the cube
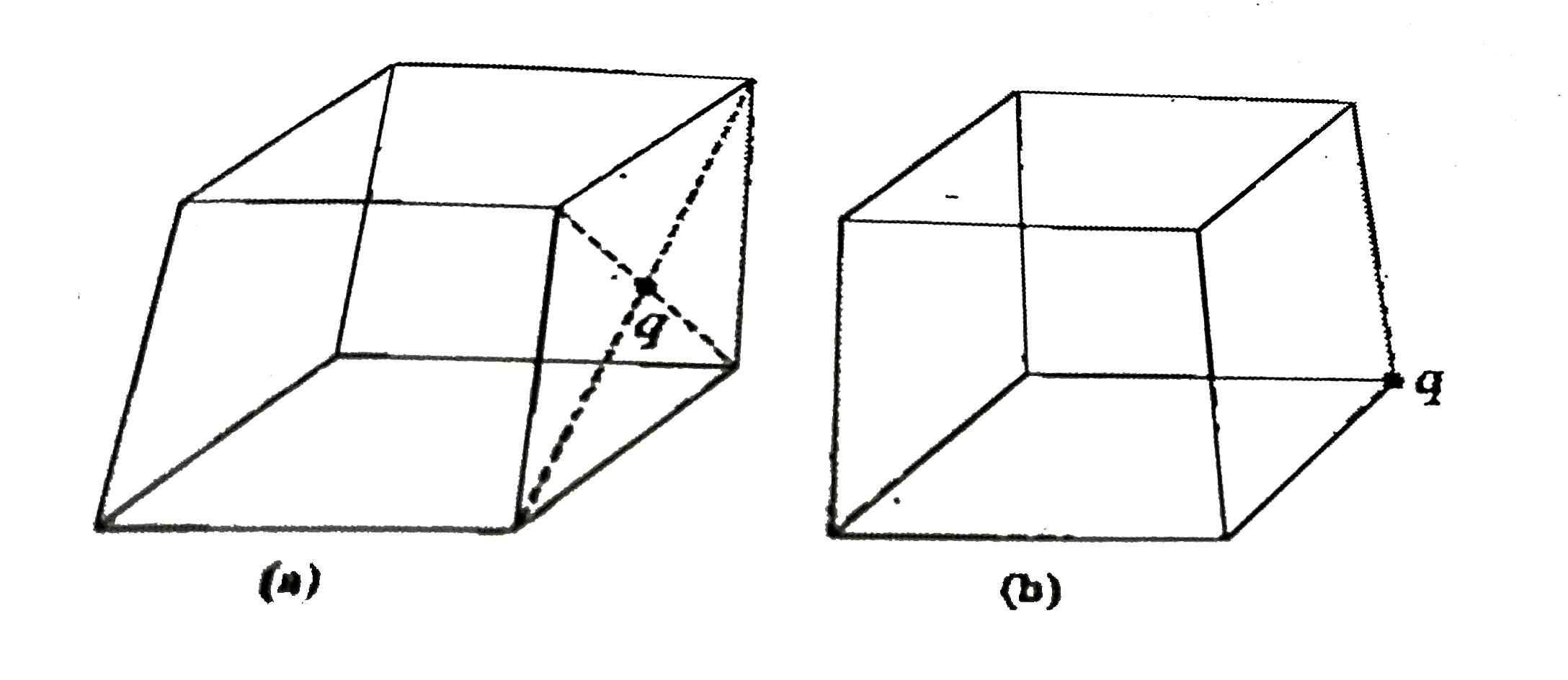
`[q/(2in_(0)),q/(8 in_(0)),q/(24 in_(0)),0]`
View SolutionA cube has sides of length L=0.2 m It is placed with one corner at the origin as shown in figure The electric field in uniform and given by `vec(E)=(2.5hat(i)-4.2hat(j))N//C` .Find the electric flux through the entire cube.

View SolutionFor a spherically symmetrical charge distribution electric field at a distance r from the centre of sphere is `vec(E)=kr^(2)hat(r)` where k is a constant what will be the volume charge density at a distance r from the centre of sphere?
View SolutionA non-conducting spherical ball of radius R contains a spherically symmetric charge with volume charge density `rho=kr^(2)` where r is the distance form the centre of the ball and n is a constant what should be n such that the electric field inside the ball is directly proportional to square of distance from the centre?
View SolutionAn infinite, uniformly charged sheet with surface charge density `sigma` cuts through a spherical Gaussian surface of radius `R` at a distance `X` from its center, as shown in the figure. The electric flux `Phi` through the Gaussian surface is .

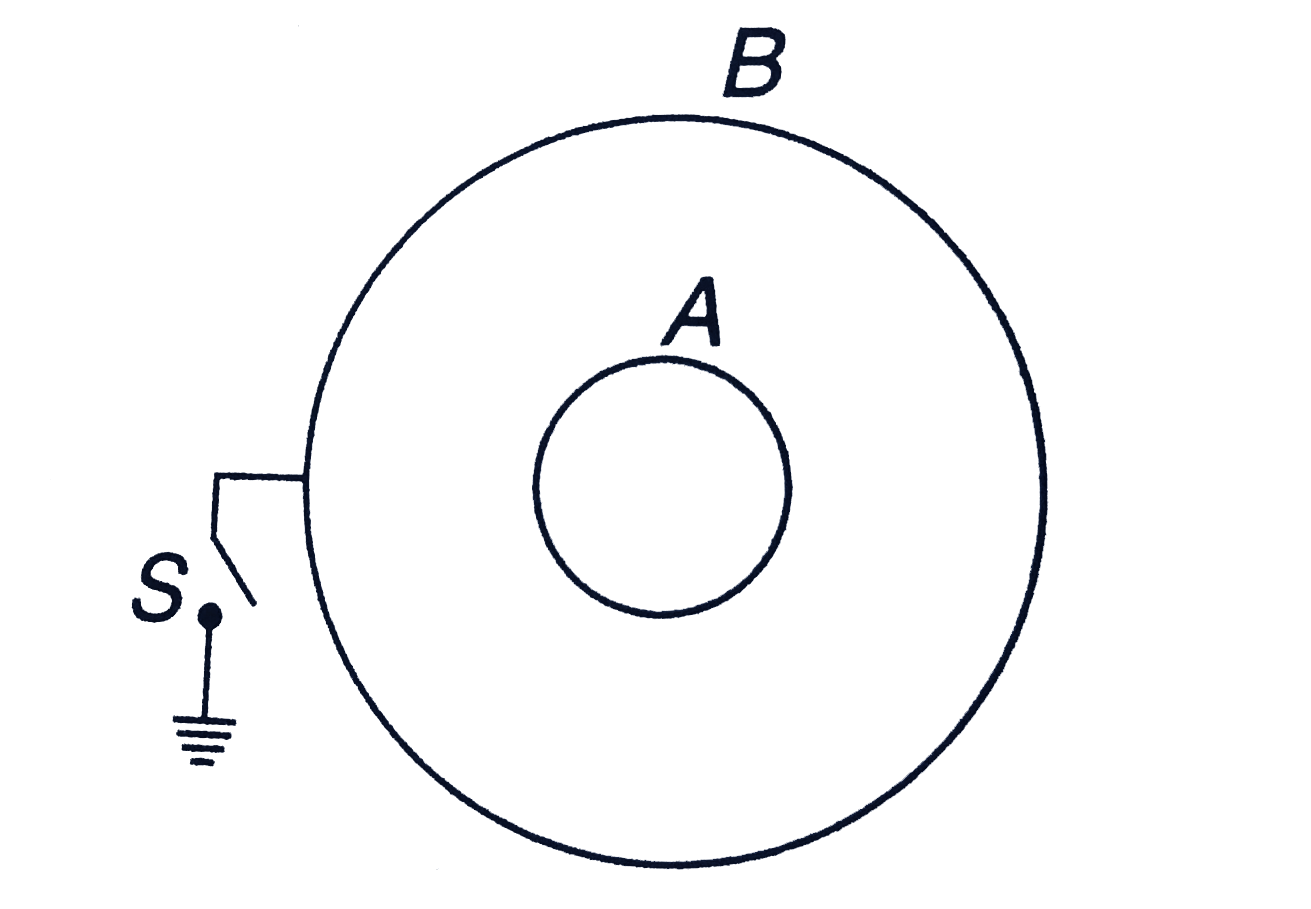
View SolutionInitially the spheres A and B are at potentials `V_A` and `V_B`. Find the potential of A when sphere B is earthed.
View SolutionFigure shows three concentric thin conducting spherical shells A, B and C of radii R, 2R and 3R. The shell B is earthed A and C are given charges q and 2q respectively. Find the charges appearing on all the surface of A,B and C.

[inner surface `(A)0,(B)-q,(C) 4/3 q`
Outer surface `(A) q, (B)-4/3 q,(C) 2/3 q]`
View SolutionThree identical metallic plates are kept parallel to one another at a separation of a and b The outer plates are connected by a thin conducting wire and a charge Q is placed on the central plate Find final charges on all the surfaces of the three plates.
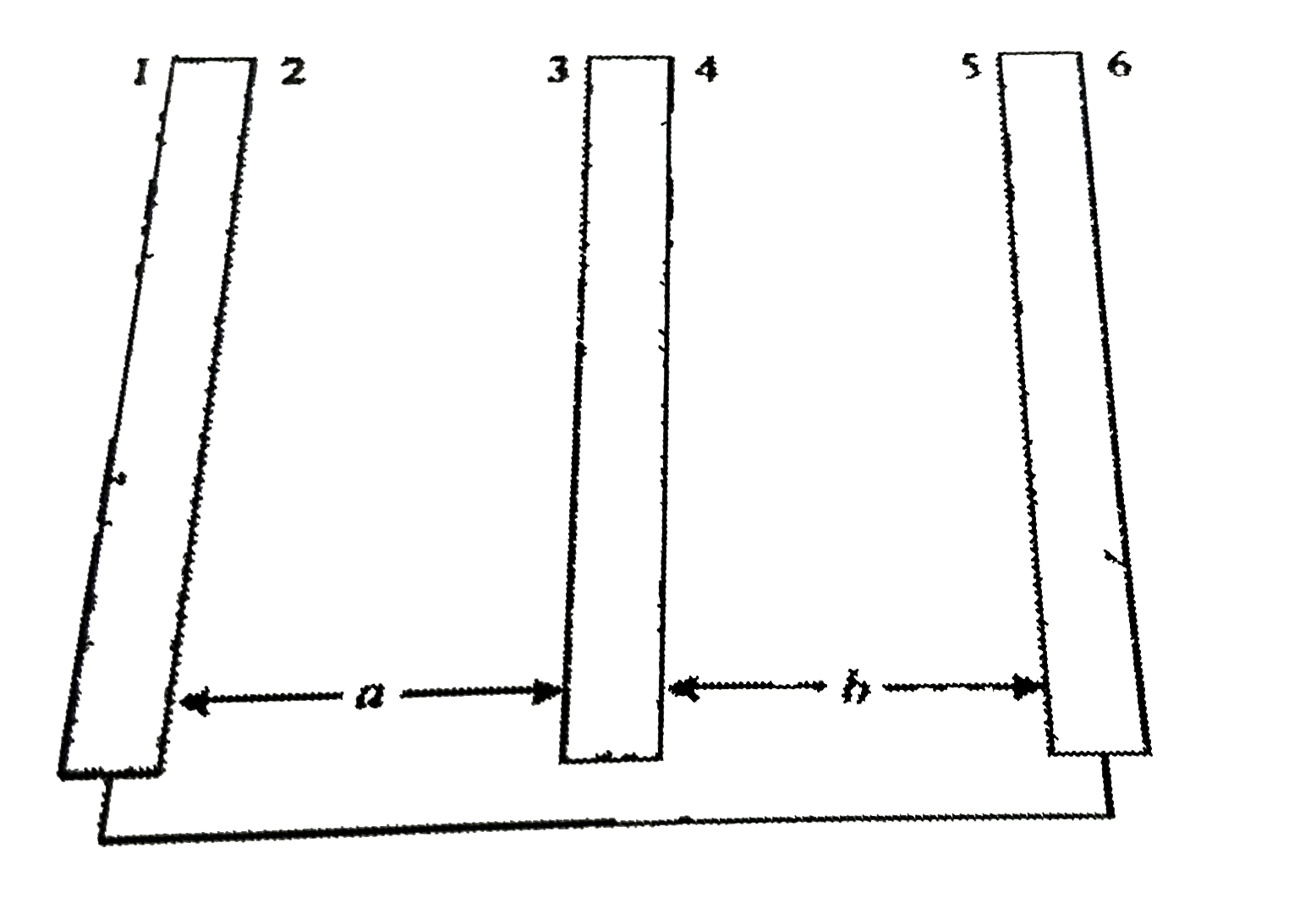
`[faces(1) Q/2,(2) -(Qb)/(a+b),(3) (Qb)/(a+b),(4)(Qa)/(a+b),(5)-(Qa)/(a+b),(6)Q/3]`
View SolutionThere are two concentration conducting spherical shells of radii r and 2r initially a charge Q is given to the inner shell Now, switch `S_(1)` is closed and opened then `S_(2)` is closed and opened and the process is repeated n times for both the keys alternatively. Find the final potential difference between the shells.

`[(1)/(2^(n+1))[(Q)/(4pivarepsilon_(0))r]]`
View SolutionAn electrometer is charged to 3 kV. Then the electrometer is touched with a neutral metal ball, mounted on an isulating rod and then the metal ball is taken away and earthed The process is done for 10 times and finally the electrometer reads 1.5 kV. After this, at least how many times must the above process be repeated in order that the electrometer reads less than 1 kV?
View SolutionWhen an uncharged conducting ball of radius `R` is placed in an external uniform electric field, a surface charge densityh `sigma = sigma_(0) cos theta` is induced on the ball's surface charge (here `sigma_(0)` is a constant, `theta` is a polar angle). Find the magnitude of the resultant electric force acting on an induced charge of the same sign.
View SolutionA point charge `q` is located at the centre of the spherical layers of uniform isotropic dielectric with relative permittivity `K`.The inside radius of the layer is equal to `a` and the outside radius is equal to `b`.The electrostatic energy inside the dielectric layer is
View SolutionA solid conducting sphere of radius a having a charge q is surrounded by a concentric conducting spherical shell of inner radius `2a` and outer radius `3a` as shown in figure. Find the amount of heat porduced when switch is closed `(k=1/(4piepsilon_0))`

View SolutionThe figure shows a conducting sphere 'A' of radius 'a' which is surrounded by a neutral conducting spherical shell B of radius 'b' `( gt a)` Initially switches `S_(1),S_(2)` and `S_(3)` are open and sphere 'A' carries a charge Q.

First the switch `'S_(1)'` is closed to connect the shell B with the ground and then opened Now the switch `'S_(2)'` is closed so that the sphere 'A' is grounded and then `S_(2)` is opened Finally, the switch `'S_(3)'` is closed to connect the spheres together. Find the heat(in Joule) which is produced after closing the switch `S_(3)` [Consider `b=4 cm a=2 cm and Q=8muc]`
View SolutionA long cylindrical shell of length l and radius a is given a uniformly distributed charge Q on its surface. If the shell is expanded uniformly to a radius b, find the work done by electrical forces in the process of expansion.
`[(lambda^(2)l)/(4pi in_(0))l n(b/a)]`
View SolutionIn a system of two concentric spherical conducting shells charge q is given to both inner and outer shells as shown in figure 1.361. Inner shell is connected to earth by a switch Find the amount of heat produced when switch is closed

`[(5Kq^(2))/(8a)]`
View SolutionTwo uniformly charged solid spheres A and B of radii a and b with charges `q_(1)` and `q_(2)` are kept at a separation r. Find the work done in disassembling the whole system into very small particles and displace the particles to infinite separation.
`[3/5 (Kq_(1)^(2))/a+3/5(Kq_(2)^(2))/b+(Kq_(1)q_(2))/r]`
View SolutionTwo uniformly charged concentric sperical shells are of radii a and b respectively. The charges on the two shells are `q_(1)` and `q_(2)` Find the work required in expanding the outer shell of radius b to increase its radius to infinity
`[-(Kq_(2)^(2))/(2b)+(Kq_(1)q_(2))/(b)]`
View Solution
Partice Exercise questions and complete solutions for chapter ELECTROSTATICS of GK PUBLICATIONS PHYSICS (HINGLISH) of Class 12
All Exercises from PHYSICS GALAXY Class 12 PHYSICS ELECTROSTATICS
- Advance MCQs
- Conceptual MCQs single option correct
- Discussion Question
- Illustrative Example
- Numerical MCQs Single options Correct
- Partice Exercise
- Partice Exercise 1.1
- Partice Exercise 1.10
- Partice Exercise 1.2
- Partice Exercise 1.3
- Partice Exercise 1.4
- Partice Exercise 1.5
- Partice Exercise 1.6
- Partice Exercise 1.7
- Partice Exercise 1.8
- Partice Exercise 1.9
- Unsolved Numberical Problems