Complete Solutions to Illustrative Example of chapter ELECTROSTATICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTROSTATICS |
| PHYSICS GALAXY | Illustrative Example |
| Number Of Questions | 95 |
| Academic Year | 2023-24 |
Given a cube with point charges q on each of its vertices. Calculate the force exerted on any of the charges due to rest of the 7 charges.
View SolutionTwo particles, each having a mass of 5 g and charge. `1.0 xx 10^(-7)` C, stay in limiting equilibrium on a horizontal. table with a separation of 10 cm between them. The coefficient of friction between each particle and the table. is the same. Find the value of this coefficient.
View SolutionTwo particles A and B having charges q and 2q respectively are placed on a smooth table with a separtion d. A third partcle C is to be clamped on the table in such a way that the particles A and B remain at rest on the table undeer electrical forces. What should at rest on the table under electrical forces. What should be the charge on C and where should it clamped?
View SolutionCharges `5.0 xx ^(-7) C and 1.0 xx 10^(-7) C` are
held fixed at the three cornners A, B, C of an equilateral
. charge at C due to the rest two.
View SolutionA particle a having a charge of `5.0 xx 10 ^(-7) C` is fixed in. a vertical wall. A second particle B of mass 100 g and. having equal charge is supended by a silk thread. of length 30 cm form the wall. The point of suspension is. 30 cm above the particle A. Find the angle of the thread. with the vertical when it stays in equilibrium.
View SolutionTen positively charged particles are kept fixed on the x-axis at points x=10cm, 20cm, 30cm, …, 100cm. The first particle has a charge `1.0xx 10^(-8)C`, the second `8xx10^(-8)` C, the third `27xx10(-8)`C and so on. The tenth particle has a charge `1000xx10^(-8)C.` find the magnitude of the electric force acting on a 1 C charge placed at the origin.
View SolutionTwo positive charges `q_(1)` and `q_(2)` are located at the points with redius vectors `r_(1)` and `r_(2)`. Find a negative charge `q_(s)` and a radius vector `r_(s)` of the point at which it has to be placed for the force acting on each of the three charges to be equal to zero.
View SolutionThree small balls, each of mass 10 gm are suspended separately from common point. by silk threads, each one meter long. The balls are identically charged and hang at the corners of an equilateral triangle of side 0.1. metre. Find the charge on each ball?
View SolutionTwo identically charged spheres are suspended by strings of equal length. The strings make an angle of `30^(@)` with each other. When suspended in a liquid of density `0.8 g// c c` the angle remains same. What is the dielectric constant of liquid. Density of sphere`=1.6 g//c c`

View SolutionA ring of radius R with a uniformly distributed charge q as shown in figure. A charge `q_(0)`, is now placed at the centre of the ring. Find the increment in-the tension in ring.

View SolutionFour small particles charged with equal positive charges Q each are arranged at the four corners of a horizontal square of side a. A unit positive charge mass m is placed at a point P, at a height h above the centre of the square. What should be the magnitude of charge Q in order that the unit charge remain in equilibrium
View SolutionTwo small particles charged with equal positive charges Q each, are fixed apart at a distance 2a. Another small particle having a charge q lies midway between the fixed charges. Show that
(i) For small displacement (relative to a) along line joining the fixed charges, the middle charge executes SHM'if it is +ve and
(ii) For small lateral displacement, it executes SHM ifit is-ve. Compare the frequencies of oscillation in the two cases
View SolutionA wooden ball covered with an aluminimum foil having a mass m hangs by a fine silk thread l metre long in a horizontal electric field E. When the ball is given an electric charge q coulomb, it stands out d metre from the vertical line passing through !he · suspension point of thread. Show that the electric field is given by
`E = (mgd)/(sqrt(l^(2)-d^(2))`
View SolutionA particle of mass m and charge q is thrown with initial velocity `v_(0)` at an angle with the horizontal. In space there exist an electric field of strength E at angle `beta` with the downward vertical away from the point of projection. Find the time of flight and range of projectile on horizontal ground
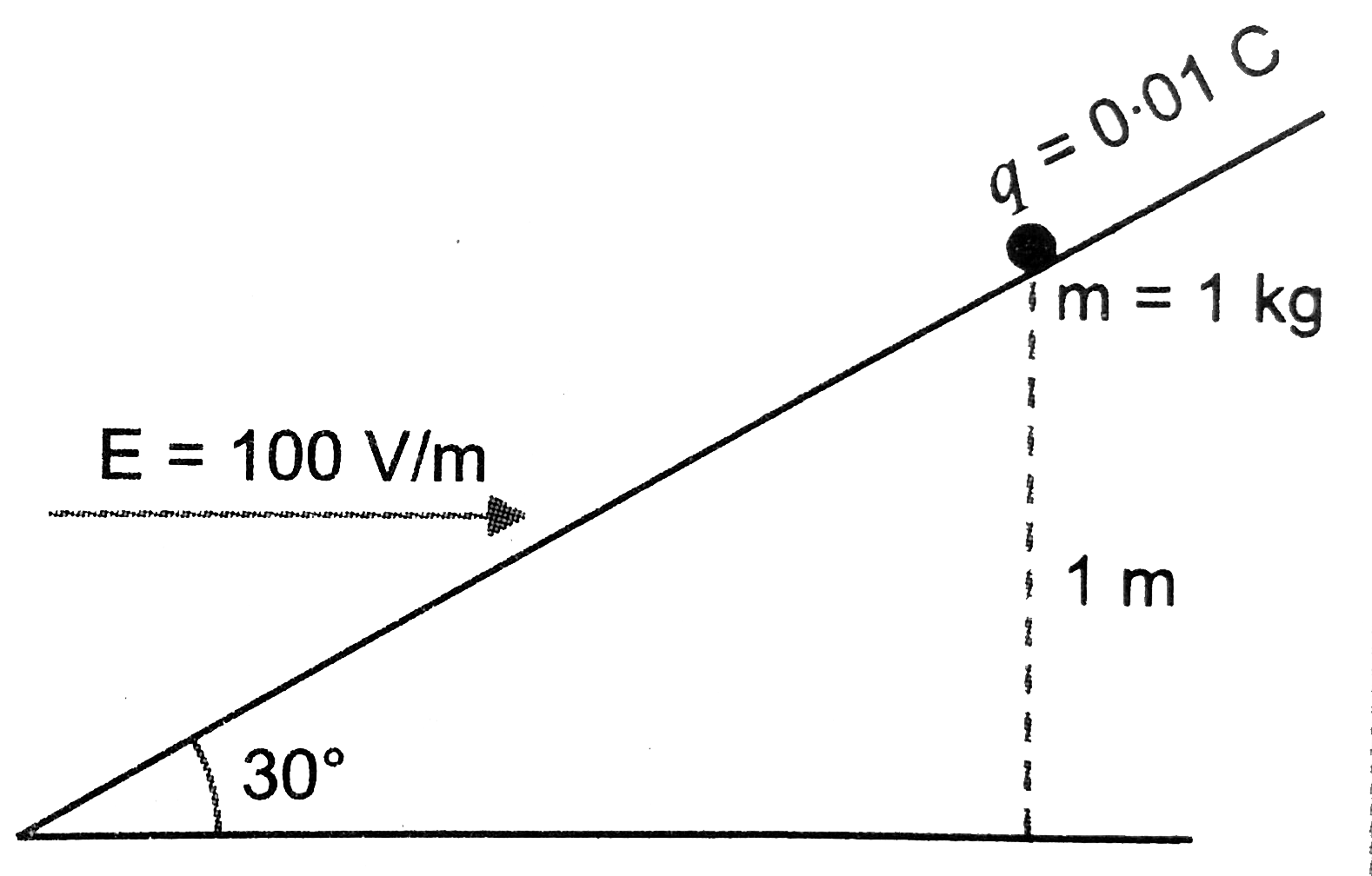
View SolutionAn inclinded plane making an angle of `30^(@)` with the horizontal electric field of `100 Vm^(-1)` as shown in Figure. A particle of mass `1 kg` and charge `0*01 C` is allowed to slide down from rest from a height of `1m`. If the coefficient of friction is `0.2`, find time taken by the particle to reach the bottom.
View SolutionA ball of mass m with a charge q can rotate in a vertical plane at the end of a string of length l in a uniform electrostatic field whose lines of force are directed upwards. What horizontal velocity must be imparted to the ball in the upper position so that the tension in the string in the lower position of the ball is 1.5 times than the weight of the ball?
View SolutionA simple pendulum has a bob of mass m = 40 gm and a positive charge `q =4 xx 10^(-6) C`. It makes 20 oscillation in 4.5 s. A vertical upward electric field of magnitude `E = 2.5 xx 10^(4) N//C` is switched on in space. How much time will the simple pendulum will now take to complete 20 oscillation.
View SolutionA bob of mass m carrying a positive charge q is suspended from a light insulating string of length l inside a parallel plate capacitor with its plates making an angle `beta` with the horizontal as shown in figure. The plates of the capacitor are connected with a battery to establish an electric field E between the plates with its upper plate negatively charged. Find the period of small oscillations of the pendulum and the angle between the thread and vertical in equilibrium position of the bob

View SolutionA rectangular tank of mass `m_(0)` and charge Q is placed over a smooth horizontal floor. A horizontal electric field£ exist in the region. Rain drops are falling vertically in the tank at the constant rate of n drops per second. Mass of each drop is m. Find velocityoftank as function of time.
View SolutionFour particles each having a charge q are placed on the four vertices of a regular pentagon. The distance of each comer from !be centre is 'a'. Find the electric field at the centre of pentagon.
View SolutionIn the given arrangement of a charged square frame made up of four wires 1, 2, 3 and 4 charged witb the linear charge density as mentioned in figure. Find electric field at centre due to this frame

View SolutionA system consits fo a thin charged wire ring of radius `R` and a very long uniformly charged thread oriented along the axis of the ring, with one of its ends coinciding with the centre of the ring. The total charge of the ring, with one of the ring so equal to `q`. The charge of the thread (per unit length) is equal to `lambda`. Find the interaction froce between the ring and the thread.
View SolutionA point charge `q` is located at the centre fo a thin ring of radius `R` with uniformly distributed charge `-q`, find the magnitude of the electric field strength vectro at the point lying on the axis of the ring at a distance `x` from its centre, if `x gt gt R`.
View SolutionA thin fixed of radius 1 metre has a positive charge `1xx10^-5` coulomb uniformly distributed over it. A particle of mass 0.9 gm and having a negative charge of `1xx10^-6` coulomb is placed on the axis at a distance of 1cm from the centre of the ring. Show that the motion of the negatively charged particle is approaximately simple harmonic. Calculate the time period of oscillations.
View SolutionA clock face has charges `-q, -2q, ,.....-12q` fixed at the position of the corresponding numerals on the dial. The clock hands do not disturb the net field due to point charges. At what time does the hour hand point in the direction of the electric field at the centre of the dial.
View SolutionConsider the classical model of an electron such that a nucleus of charge +e is uniformly distributed within a sphere of radius`2Å`. An electron of charge -e at a radial distance `1Å` moves inside this sphere. Find the force a!tracting the electron on to the centre of the sphere. Calculate the frequency with which the electron would oscillate about the centre of the sphere, if released from rest at this radial distance.
View SolutionA positive charge q is placed in front of conducting solid cube at a distance d from its centre. Find the electric field at the centre of the cube due to the charges appearing on its surface.
View SolutionA large nonconducting surface has a uniform charge density `sigma`. A small circular hole ofradius R is cut in the middle of the sheet, as shown in figure. Ignore fringing of the field lines around all edges calculate the electric field at' pointP, a distancez from the centre of the hole along its axis.

View SolutionA thin insulating wire is stretched·along the diameter of an. insulated circular hoop of radius R. A small bead of mass m and charge-q is threaded onto the wire. Two small identical charges are tied to the hoop at points opposite to each other, so that the diameter passing through them is perpendicular to the thread as shown in figure. The bead is released at a point which.is located at a distance `x_(0)` from the centre of the hoop. Assume that `x_(0) lt lt R`.
(a) What is the resultant force acting on the charged bead?
(b) Describe the motion of the bead after it is released X
(c) Use the assumption that `(x)/(R) lt lt 1` to obtain an approximate equation of motion, and find the displacement and velocity of the bead as functions of time
(d) When will the velocity of the bead will bcome zero for the first time?

View SolutionAn infinitely long cylindrical shell ofinner radius `r_(1)` and outer radius `r_(2)` is charged in its volume with a volume charge density which varies with distance from axis of cylinder as `p = blr C//m^(3)` which C is a positive constant and r is the distance from axis of cylinder. Find the electric field intensity at a point P at a distance x from axis of cylinder
View SolutionAn infinitely long cylindrical surface density `sigma = sigma_(0) cos varphi`. Where `varphi` is the polar angle of the cylindrical coordinate system whose `z` axis coincides with the axis of the given surface. Find the magnitude and direction of the electric field strength vector on the `z` axis.
View SolutionA thin nonconducting ring of radius `R` has a linear charge density `lambda = lambda_(0) cos varphi`, where `lambda_(0)` is a constant , `phi` is the azimutahl angle. Find the magnitude of the electric field strength
(a) at the centre of the ring ,
(b) on the axis of the ring as a function of the distance `x` from its centre. Investegation the obtained function at `x gt gt R`.
View SolutionA ball of radius `R` carries a positive charge whose volume density depends only on a separation `r` from the ball's centre as `rho = rho_(0) (1 - r//R)`, where `rho_(0)` is a constant. Asumming the permittivites of the ball and the enviroment to be equal to unity find :
(a) the magnitude of the electric field strength as a function of the distance `r` both inside and outside the ball :
(b) the maximum intensity `E_(max)` and the corresponding distance `r _(m)`.
View SolutionA point charge `q_1 = 4.00 nC` is placed at the origin, and a second point charge `q_2 = -3.00 nC`, placed on the x-axis at x = + 20.0 cm. A third point charge `q_3 = 2.00 nC` is placed on the X-axis between `q_1, and q_2`. (Take as zero the potential energy of the three charges when they are infinitely far apart).
(a) What is the potential energy of the system of the three charges if `q_3` is placed at x= + 10.0 cm?
(b) Where should `q_3` be placed to make the potential energy of the system equal to zero?
View SolutionA particle of mass `400 mg` and charged with `5 xx 10^(-9) C` is moving directly towards a fixed positive point charge of magnitude `10^(-8) C`. When it is at a distance of 10 cm from the fixed positive point charge it has a velocity of 50 cm/s. At what distance from the fixed point charge will the particle come momentarily to rest ? Is the acceleration constant during the motion ?
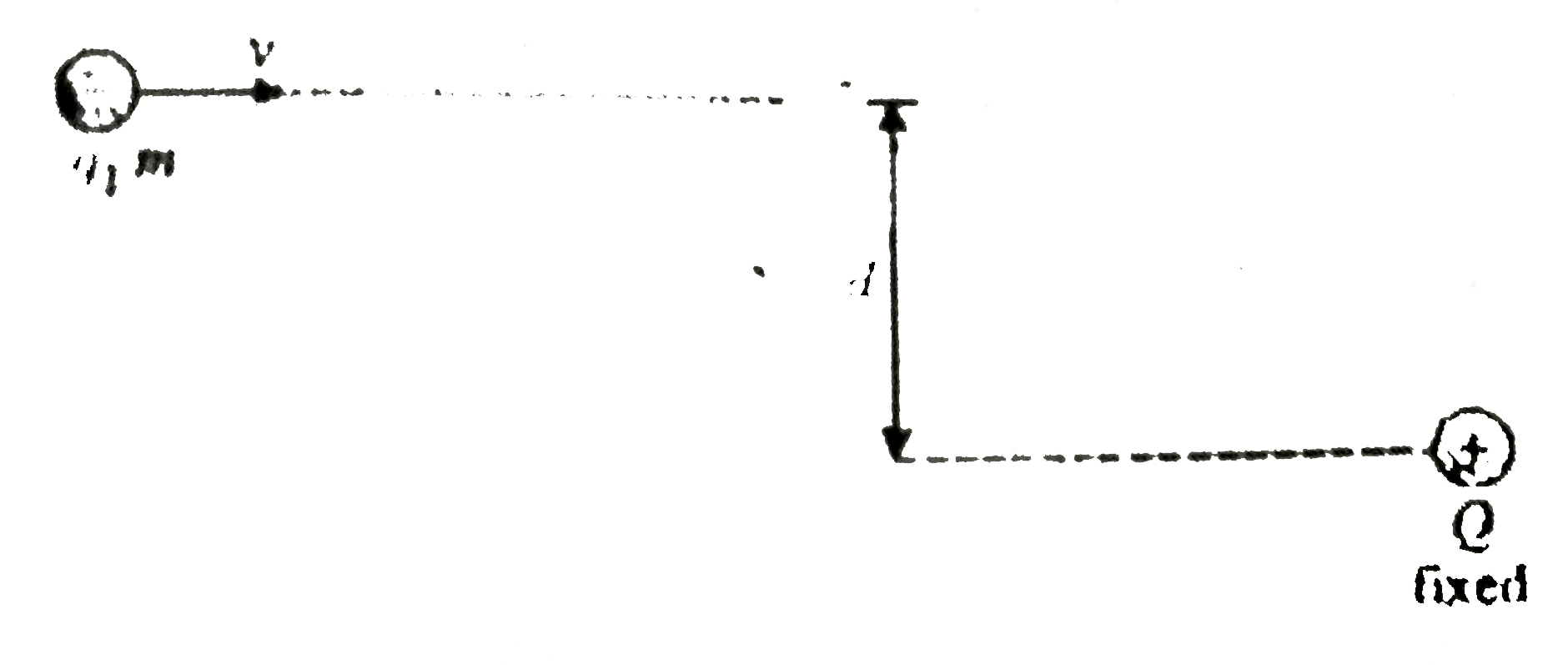
View SolutionFigure shows a charge +Q clamped at a point in free space. From a large distance another charge particle of charge -q an.d mass m is thrown toward +Q with an impact parameter d as shown with speed v. Find the distance of closest approach of the two particles.
View SolutionA particle of mass 40 mg and carrying a charge `5 xx 10^(-9) C` is moving directly towards a fixed positive point charge on magnitude `10^(-8) C`. When it is at a distance of 10 cm from the fixed positive point charge it has a velocity of `50 cm s^(-1)` at what distance from the fixed point charge will the particle come momentarily to rest ? Is the acceleration constant during motion?
View SolutionThree point charges q, 2q and 8q are to be placed on a
. 9cm long straight line. Find the
. positions where the charges shouldbe placed such that the potential energy
. of this sysrem is minimum. In this situation, what is the
. electric field at the charge q due to the other two charges?
View SolutionTwo fixed, equal, positive charges, each of magnitude `5xx10^-5` coul are located at points A and B separated by a distance of 6m. An equal and opposite charge moves towards them along the line COD, the perpendicular bisector of the line AB.
The moving charge, when it reaches the point C at a distance of 4m from O, has a kinetic energy of 4 joules. Calculate the distance of the farthest point D which the negative charge will reach before returning towards C.

View SolutionTwo small identical balls lying on a horizontal plane are connected by a weightless spring. One ball (ball 2) is fixed at O, and the other (ball 1) is free. The balls are charged identically as a result of which the spring length increases `eta=2` times. Determine the change in frequency.

View SolutionA small particle has charge `-5.00muC` and mass `2.00 xx 10-4` kg. It moves from point A where the electric potential is `V_A = +200 V`. to point B, where the electric potential is `V_B=+ 800 V`. The electric force is the only force acting on the particle. The particle has speed `5.00 m/s` at point A. What is its speed at point B? is it moving faster or slower at B than at A. Explain,
View SolutionA particle having a charge`+ 3 xx 10^(-9 C` is placed in a uniform electric field directed toward left. It is released from rest and moves a distance of 5 cm after which its kinetic energy is found to be `4.5 xx 10^(-5) J`.
(a) Calcnalate the work done by the electrical force on the particle
(b) Calculate the magnitude of the electric field.
(c) Calculate the potential of starting point with respect to the end point of particle's motion.

View SolutionAn electric field `vecE = vec I Ax` exists in the space, where `A= 10 V m ^(-2).` Take the potential at (10m, 20m ) to be zero. Find the potential at the origin.
View SolutionFind `V_(ba)`, if `12 J` of work has to be done against an electric field to take a charge of `10^-2` C from a to b.
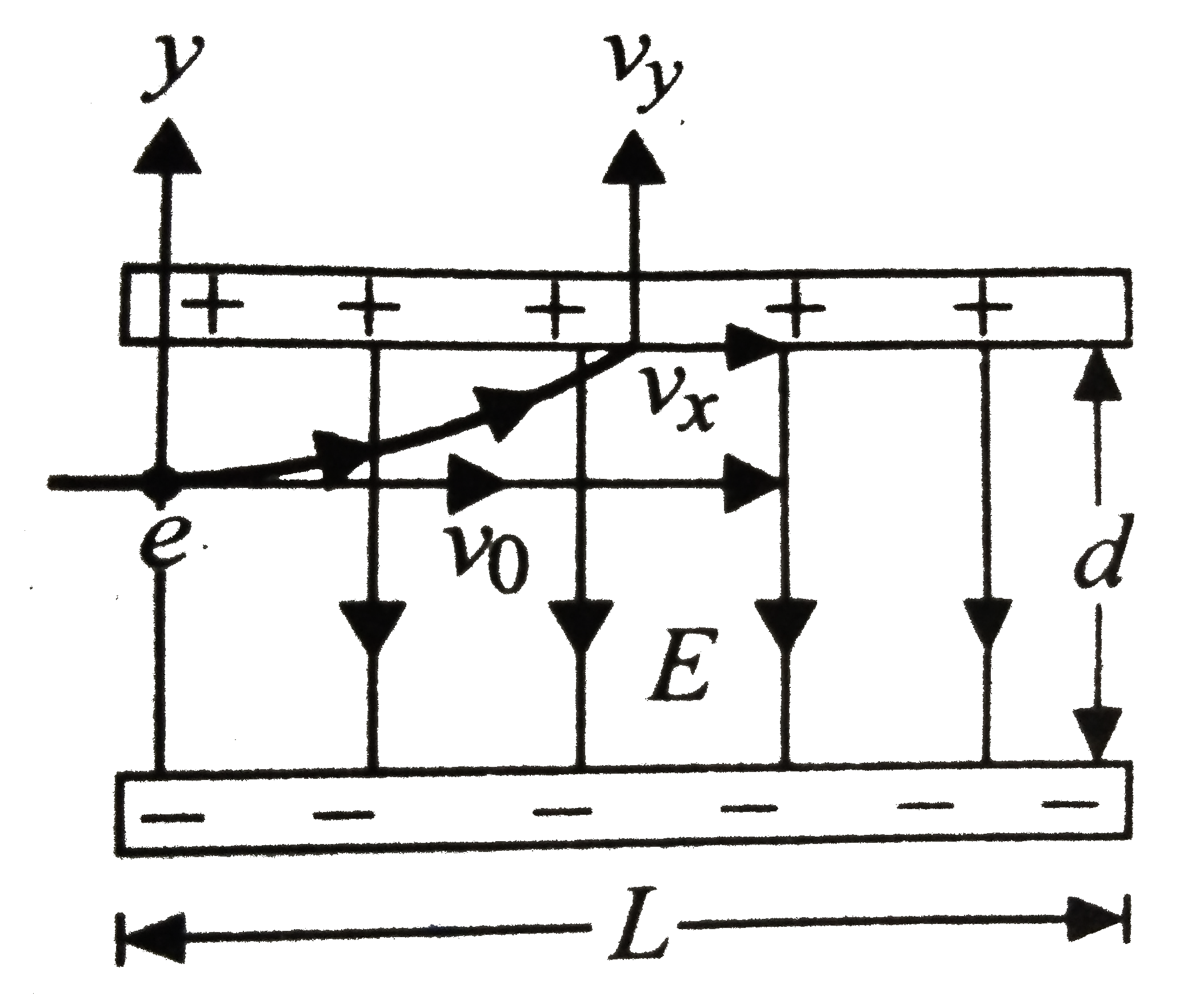
View SolutionA particle of mass `9xx10^(-31)` kg having a negative charge of `1.6xx10^(-19)C` is projected horizontally with a velocity of `10^(6)ms^(-1)` into a region between two infinite horizontal parallel plates of metal. The distance between the plates is `d=0.3cm` and the particle enters 0.1cm below the top plate, THe top and bottom plates are connected, respectively to the positive and negative terminal of a 30V battery. Find the components of the velocity of the particle just before it hits one of the plates.
View SolutionThere are two large parallel metallic plates `S_(1)` and `S_(2)` carrying surface charge densities `sigma_(1)` and `sigma_(2)` respectively `(sigma_(1) gt sigma_(2))` placed at a distance d apart in vacuum. Find the work done by the electric field in moving a point charge q at distance `a(a lt d)` from `S_(1)` towards `S_(2)` along a line making an angle `pi//4` with the normal to the plates.
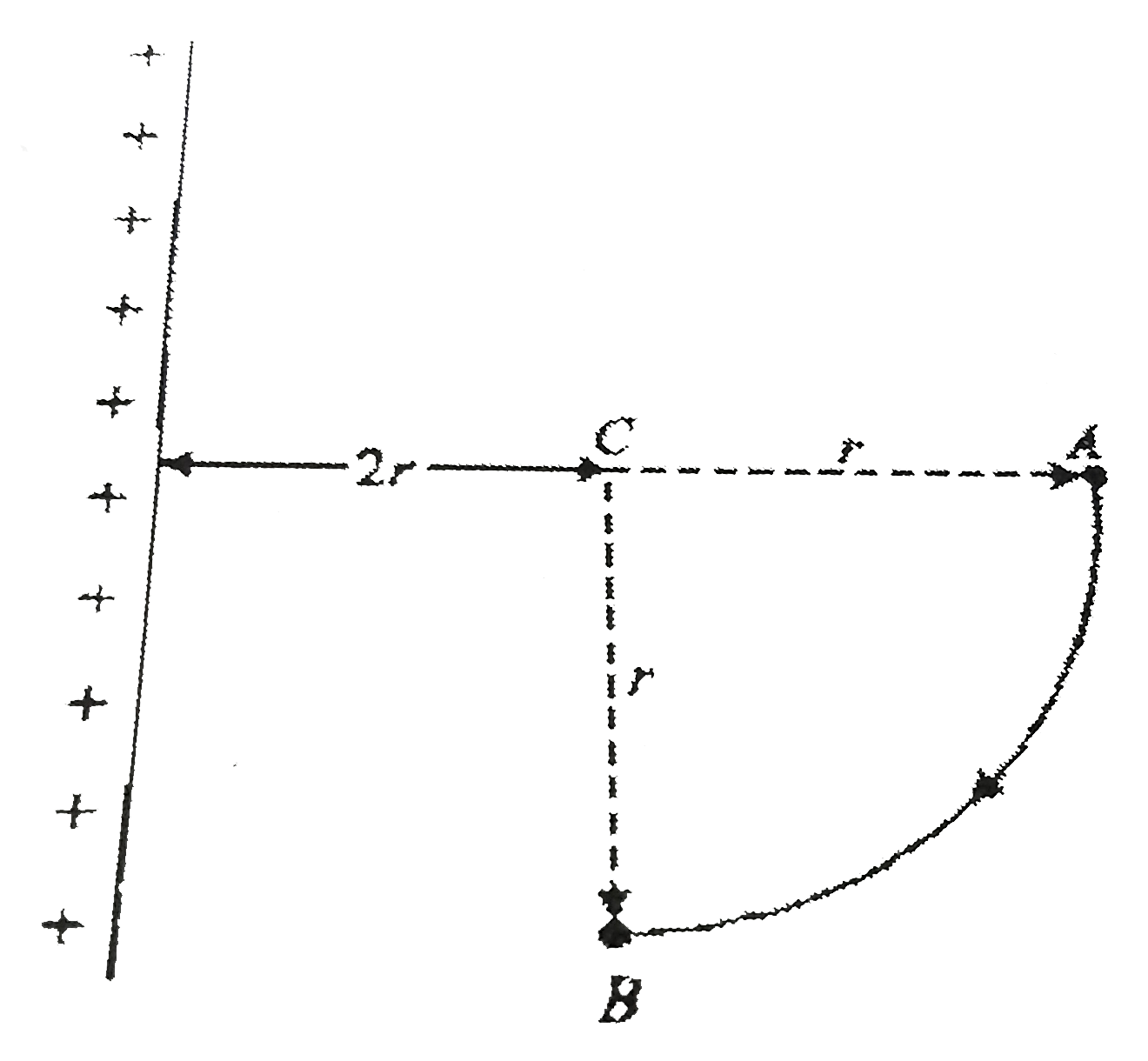
View SolutionA charge `q_(0)` is transported from point A to B along the arc AB with centre at C as shown in figure near a long charged wire with linear density A. lying in the same plane. Find the work done in doing so.
View SolutionSome equipotential surfaces are shown in figure . The magnitude and direction of electric field is

View SolutionCalculate the potential due to a thin uniformly charged rod of length L at the poiot P shown in figure. The lioear charge density of the rod is `lambda C//m`

View SolutionTwo charges `-2Q` abd `Q` are located at the points with coordinates `(-3a, 0)` and `(+3a, 0)` respectively in the x-y plane. (i) Show that all points in the x-y plane where the electric potential due to the charges is zero, on a circle. Find its radius and the location of its centre (ii) Give the expression V(x) at a general point on the x-axis and sketch the function V(x) on the whole x-axis. (iii) If a particle of charge +q starts from rest at the centre of the circle, shown by a short quantitative argument that the particle eventually crosses the circule. Find its speed when it does so.
View SolutionThere is an infinite straight chain of alternating charges q and -q. The distance between the two neighbouring charges is equal to a. Find the interaction energy of any charge with all the other charges.
View SolutionA uniform electric field of `100 V//m` is directed at `3^@` with the positive x-axis as shown in figure. Find the potential difference `V_(BA)` if `OA=2`m and `OB=4 m.`

View SolutionThe potential at a point in space depends only upon the x-coordinate and it is given as
`V = (1000)/(x)+(1500)/(x^(2))+(500)/(x^(3))` Determine the electric field strength at point where `x = 1 m`.
View SolutionDetermine the electric field strength vector in a region if in space the potential of this field depends on x and y coordinates as `V=a(x^(2)-y^(2))`.
View SolutionA charge Q is distributed over two concentric hollow spheres of radii r and `R (gt r)` such that the surface charge densities are equal. Find the potential at the common centre.
View SolutionA conducting liquid bubble of radius a and thickness ` t ( tltlt a)` is charged to potential `V`. If the bubble collapses to a droplet , find the potential on the droplet .
View SolutionFind the electric field potentail and strength at the centre of a hemisphere fo raidus `R` ahcged uniformly with the the surface density `sigma`.
View SolutionOn a thin rod oflength `l= 1 m`, lying along the x-axis with one end at the origin x = 0, there is uniformly distributed charge per unit length `lambda = Kx`, where K =constant `= 10^(-9) cm^(-2)` Find the work done in displacing a charge `q = 1000 muC` from a point `(0,sqrt(0.44 m)"to"(0, Im))`.
View SolutionA spherical drop of water carrying a charge of `3 xx 10^(-10) C` has potential of 500V at its surface. When two such drops having same charge and radius combine to from a single spherical drop, what is the potential at the surface of the new drop?
View SolutionFind the potential of an isolated ball-shaped conductor with a charge q of radius `R_(1)` surrounded by an adjacent concentric layer of dielectric with dielectric constant k and outer radius `R_(2)`
View SolutionThree concentric spherical metallic shells A, B and C of radii a, b and c (a lt b ltc) have surface charge densities `sigma`, `-sigma` and `sigma` respectively.
`(i) Find the potential of the three shells A, B and C.
(ii) If the shells A and C are at the same potential, obtain the relation between the radii a, b and c.
View SolutionA short electric dipole is situated at the origin of coordinate axis with its axis along x-axis and equator along y-axis. It is found that the magnitudes of the electric intensity and electric potential due to the dipole are equal at a point distance `r=sqrt(5) m` from origin. Find the position vector of the point in first quadrant.
View SolutionProve that the frequency of oscillation of an electric dipole of moment p and rotational inertia `I` for small amplitudes about its equilibrium position in a uniform electric field strength E is `1/(2pi) sqrt(((pE)/I))`
View SolutionA particle of mass m and charge `+q` is located midway between two fixed charged particles each having a charge `+q` and at a distance 2L apart. Assuming that the middle charge moves along the line joining the fixed charges, calculate the frequency of oscillation when it is displaced slightly.
View SolutionA water molecule is placed at a distance l from the line carrying linear charge density `lambda` . Find the maximum force exerted on the water molecule. The shape of water molecule and the partial charges on Hand O atoms are shown in figure

View SolutionTwo thin parallel threads carry a uniform charge with linear densities `lambda` and `-lambda` . The distance between the threads is equal to `l`. Find the potential of the electric field and the magnitude of its strength vector at the distance `r gt gt l` at the angle `theta` to the vector 1 (fig).

View SolutionShow that, for a given dipole, V & E cannot have the same magnitude at distance less than 2m from the dipole. Suppose that the distance is `sqrt(5)m`, determine the directions along which V & E are equal in magnitude.
View SolutionA closed cylinder is placed in uniform electric field `E` parallel to the axis of the cylinder. Find electric flux passing through cylinder.
View SolutionThe electric field in a region is given by `E=ahati+bhatj`. Hence as and b are constants. Find the net flux passing through a square area of side `I` parallel to y-z plane.
View SolutionTwo mutually perpendicular infinite wires along x-axis and y-axis carry charge densities `lambda_(1)` and `lambda_(2)` (see figure). The 1 electric line of force at P is along the line `y=(1)/(sqrt(3))x`, where P is also a point lying on the same line, then find `lambda_(1)//lambda_(2)`

View SolutionFind the electric flux coming out from one race of a cube of edge a, centre of which a point charge q is placed
View SolutionThe cylinder of previous example is now tilted by an angle `theta` from vertica. Find the flux crossing the cylinder.

View SolutionThe electric fields in a region is given by `vec(E)=E_(0)(x)/(L)hat(i)` ,Find the charge contained inside a cubical volume bounded by the surface `x=0,x=L,y=0,y=L,z=0,z=L`.
View SolutionFigure shows an imaginary cube of side a. A uniformly charged rod of length a moves towards right at a constant speed v. At `t=0`
the right end of the just touches the left face of the cube. Plot a graph between electric flux passing through the cube versus time.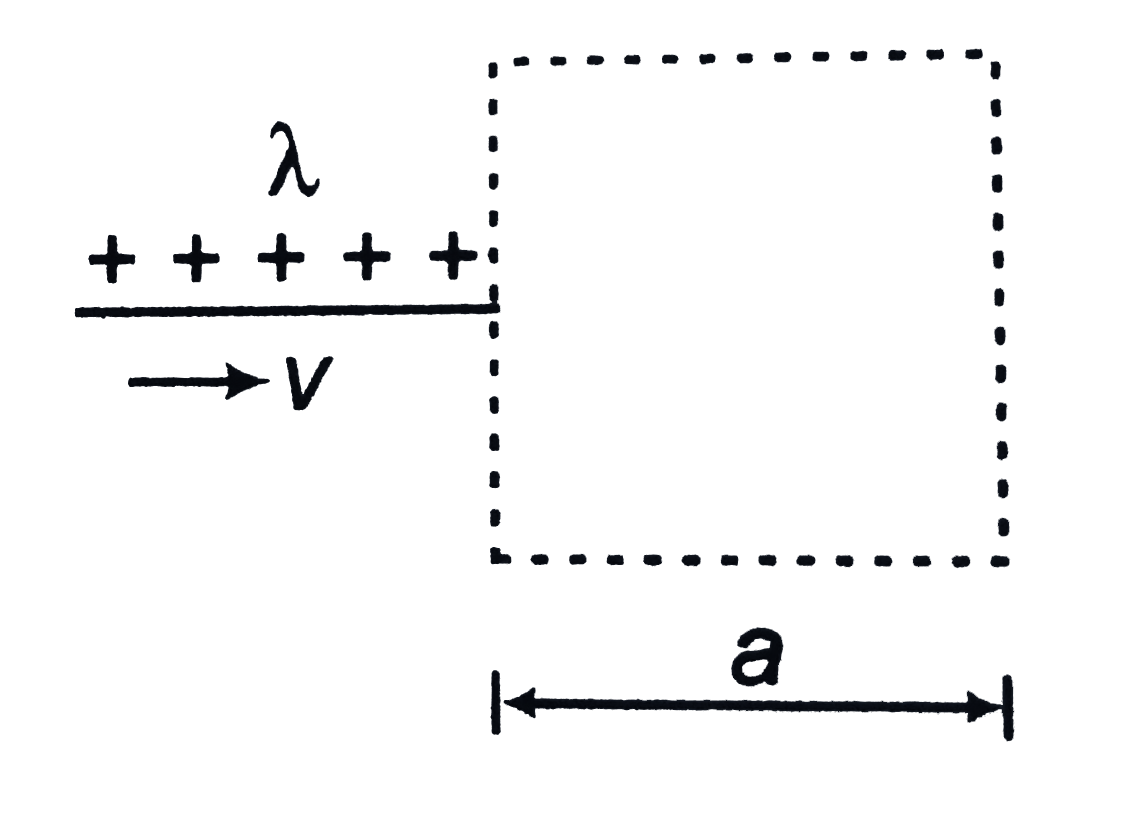
View SolutionThe field potentail in a certain region of space depends only on the `x` coordinate as `varphi = -ax^(2) + b`, where `a` and `b` are constants. Find the distribution of the space charge `rho (x)`.
View SolutionThe electrostatic potential inside a charged spherical ball is given by `phi=ar^2+b` where r is the distance from the centre and a, b are constants. Then the charge density inside the ball is:
View SolutionThe intensity of an electric field depends only on the coordinates x and y as follows,
`E = (a(xhati +y hatj))/(x^(2)+y^(2))` where, a is constant and `hati` and `hatj` are the unit vectors of the x and y axes. Find the charges within a sphere of radius R with the centre at the origin.
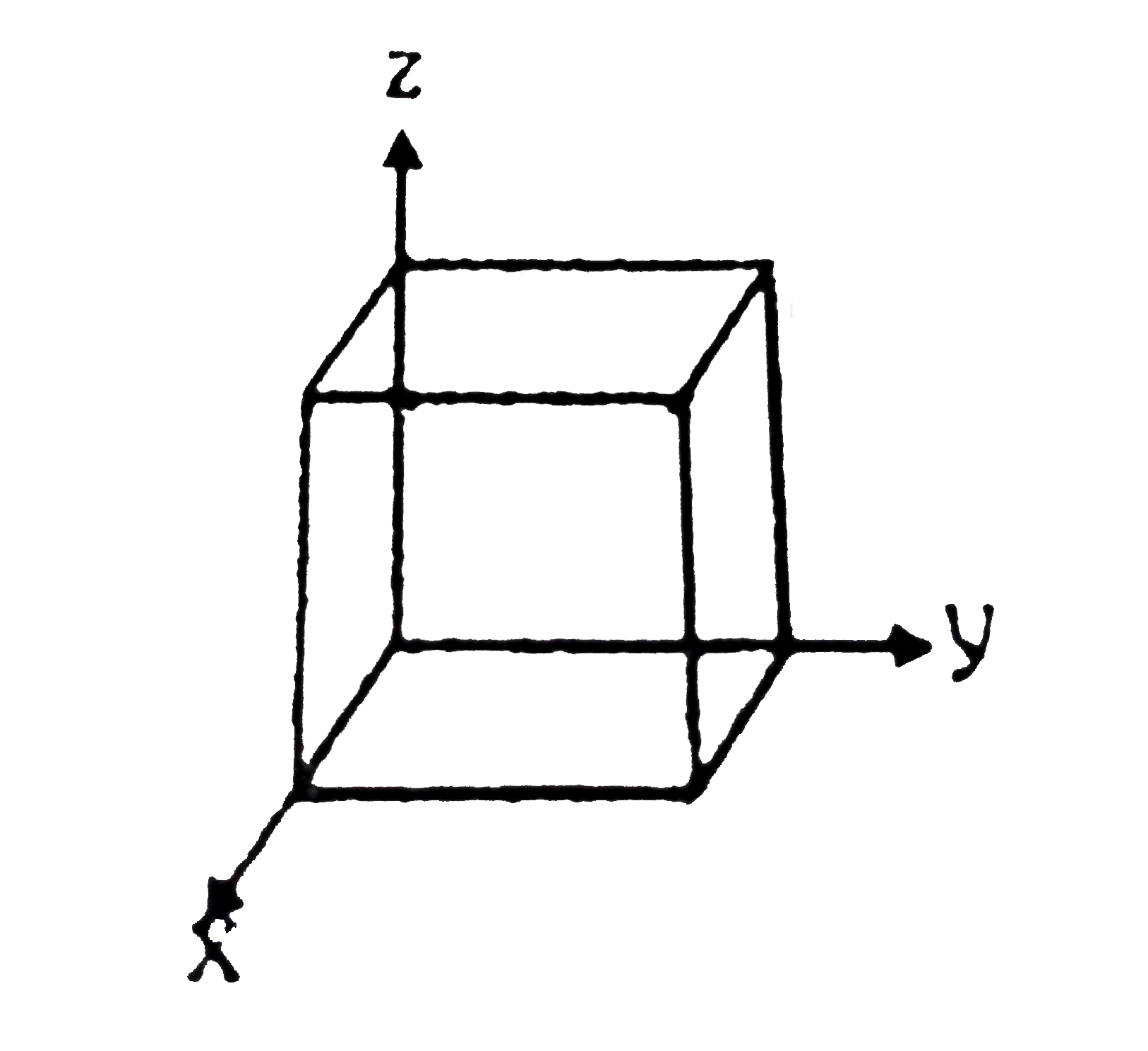
View SolutionElectric field in a region is given by `vec(E)=-4xhat(i)+6yhat(j)`. The charge enclosed in the cube of side `1 m` oriented as shown in the diagram is given by `alpha in_(0)`. Find the value of `alpha`.
View SolutionA point light source of `100W` is placed at a distance x from the centre ofa hole ofradius R in a sheet as shown in figure, Find the power passing through the hole in sheet

View SolutionA point charge q is placed at the centre of the cubical box. Find, (a) total flux associated with the box (b) flux emerging through each face of the box (c) flux throngh shaded area of surface

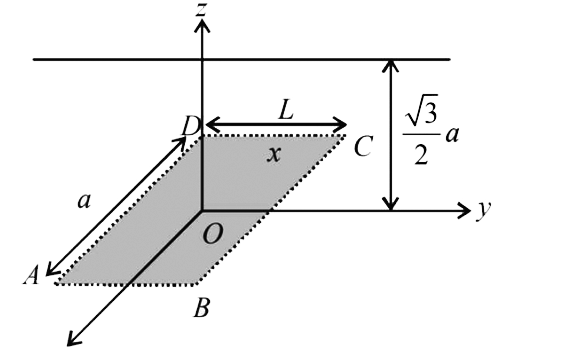
View SolutionAn infinity long uniform line charge distribution of charge per unit length `lambda` lies parallel to the y-axis in the `y-z` plane at `z=sqrt3/2` a(see figure). If the magnitude of the flux of the electric field through the rectangular surface ABCD lying in the `x-y` plane with its centre at the origin is `(lambdaL)/(nepsilon_0)` (`epsilon_0=` permittivity of free space), then the value of n is
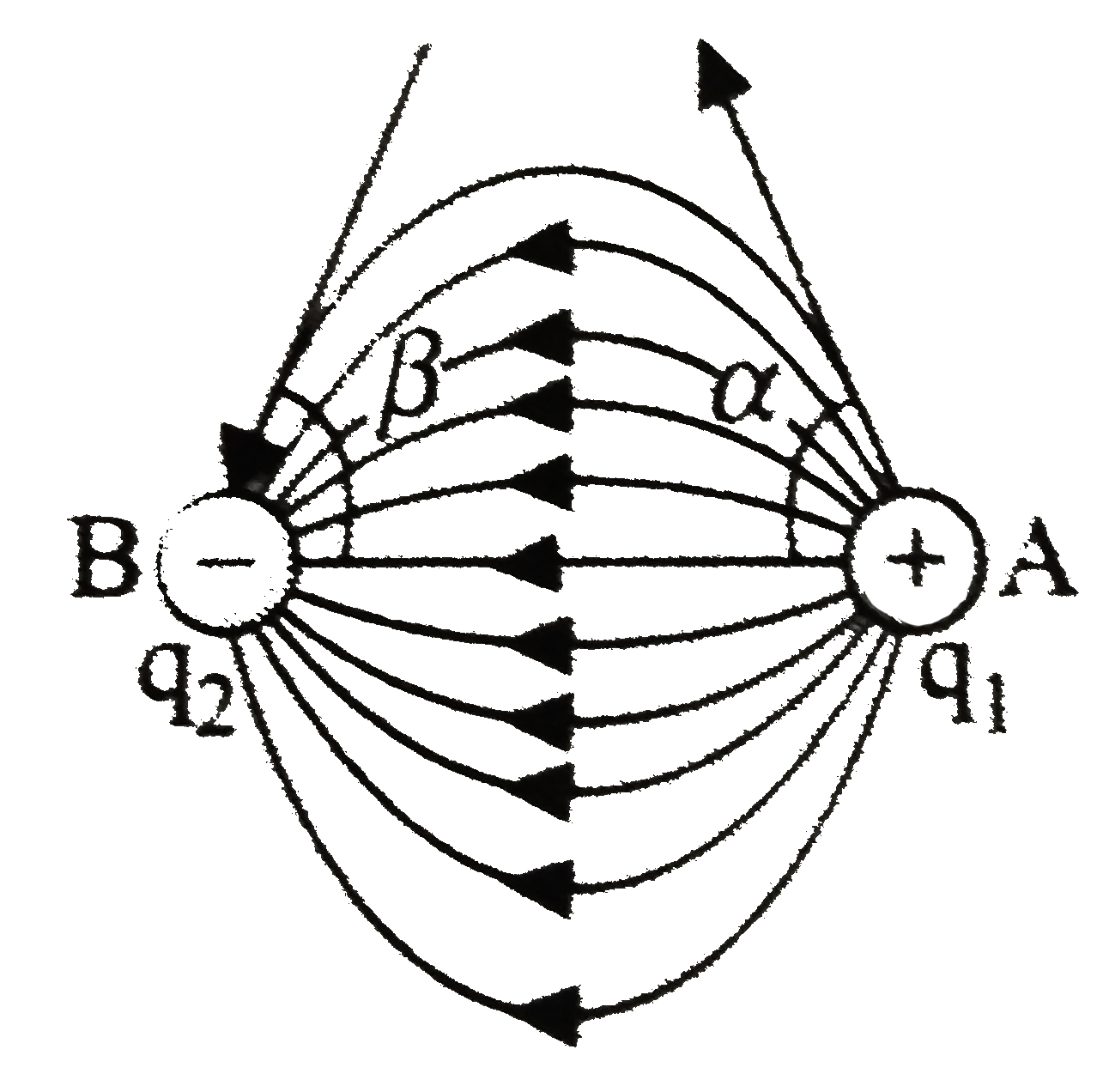
View SolutionTwo charges`+q_(1)` and `-q_(2)` are placed at A and B respectively. A line of force emanates from `q_(1)` at an angle `alpha` with the line AB. At what angle will it terminate at `-q_(2)` ?
View SolutionA point charge q is placed on the top of a cone of semi vertex angle `theta`. Show that the electric flux through the base of cone is `(q(1-costheta))/(2epsilon_0)`
View SolutionA soap bubble of radius `r` is formed inside another soap bubble of radius `R (gt r)`. The atmospheric pressure is `P_(0)` and surface tension of the soap solution is T. Calculate change in radius of the smaller bubble if the outer bubble bursts. Assume that the axcees pressure inside a bubble is small compared to `P_(0)`.
View SolutionA soap bubble of radius r and surface tension T is given a potential V. Show that the new radius R of the bubble is related with the initial radius by the equation
`P(R^(3) -r^(3)) +4T (R^(2)-r^(2)) = (in_(0)V^(2)R)/(2)` where P is the atmospheric pressure.
View SolutionThe minimum strength of a uniform electric field which can tear a conducting uncharged thin-walled sphere into two parts is known to be `E_(0)`. Determine the minimum electric field strength `E_(1)` required to tear the sphere of twice as large radius if the thickness ofits walls is the same as in the former case.
View SolutionThe point charge `q` is within the cavity of an electrically neutral conducting shell whose outer surface has spherical shape. Find the potential `V` at a point `P` lying outside the shell at distance `r` from the center `O` of the outer sphere.
 .
.
View SolutionA charge Q is placed at the centre of an uncharged, hollow metallic sphere of radius a. (a) Find the surface charge density on the inner surface and on the outer surface. (b) If a charge q is put on the sphere, what would be the surface charge densities on the inner and the outer surface? (c) Find the electric field inside the sphere at a distance x from the centre in the situations (a) and (b).
View SolutionA charge q is distributed uniformly on the surface of a sold sphere of radius R. It covered by a concentric hollow conduction sphere of radius `2R`. Find the charges inner and outer surface of hollow sphere if it is earthed.

View SolutionThere are four concentric shells A,B, C and D of radii `a,2a,3a` and `4a` respectively. Shells B and D are given charges `+q` and `-q` respectively. Shell C is now earthed. The potential difference `V_A-V_C` is `k=(1/(4piepsilon_0))`
View SolutionThere are two uncharged identical metallic spheres of radius a, separated a distance d. A charged metallic sphere (charge q) of sarue radius is brought and touches sphere 1. After some time it is moved away to a far off distance. After this, the sphere 2 is earthed. Find the charge on sphere 2.

View SolutionFigure (a) shows a shall of radius R having charge `q_(1)` uniformly distributed over it. A point charge q is placed at the centre of shell. Find amount of work required to increase the radius of shell from R to `R_(1)` as shown in figure (b).

View SolutionFind the electrostatic energy stored in a cylindrical shell of length I, inner radius a and outer radius b, coaxial with a uniformly charged wire with linear charge density `lambda C//m`.
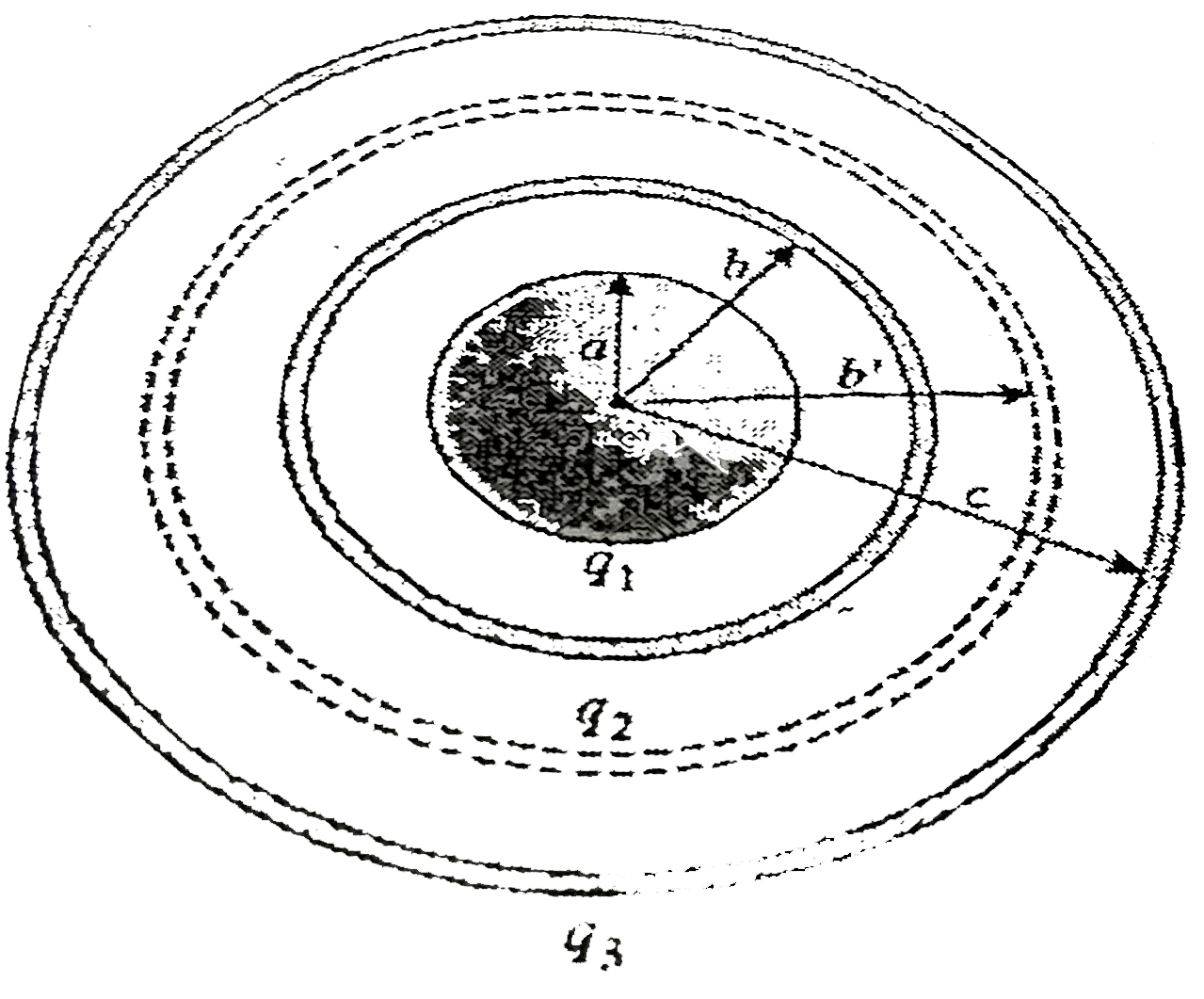
View SolutionThree shells are shown carrying charge `q_(1), q_(2)` and `q_(3)` and of radii a, band c respectively. If the middle shell expands from radius b to `b' (b' lt c)`. Find the work done by electric field in process.
View SolutionA point charge `q` is located at the centre `O` of a spherical uncharged coducting layer provided with small orifice. The inside and outside radii of the layer are equal to a and `b` respectively. The amount of work that has to be performed to slowly transfer the charge `q` from teh point `O` through the orifice and into infinity is

View Solution
Illustrative Example questions and complete solutions for chapter ELECTROSTATICS of GK PUBLICATIONS PHYSICS (HINGLISH) of Class 12
All Exercises from PHYSICS GALAXY Class 12 PHYSICS ELECTROSTATICS
- Advance MCQs
- Conceptual MCQs single option correct
- Discussion Question
- Illustrative Example
- Numerical MCQs Single options Correct
- Partice Exercise
- Partice Exercise 1.1
- Partice Exercise 1.10
- Partice Exercise 1.2
- Partice Exercise 1.3
- Partice Exercise 1.4
- Partice Exercise 1.5
- Partice Exercise 1.6
- Partice Exercise 1.7
- Partice Exercise 1.8
- Partice Exercise 1.9
- Unsolved Numberical Problems