Complete Solutions to Numerical MCQs Single options Correct of chapter ELECTROSTATICS of Class 12 book with complete answers and questions

A particle of charge `-q` and mass m moves in a circle of radius r around an infinitely long line charge of linear charge density `+lamda`. Then, time period will be
where , `k=1/4piepsilon_0)`

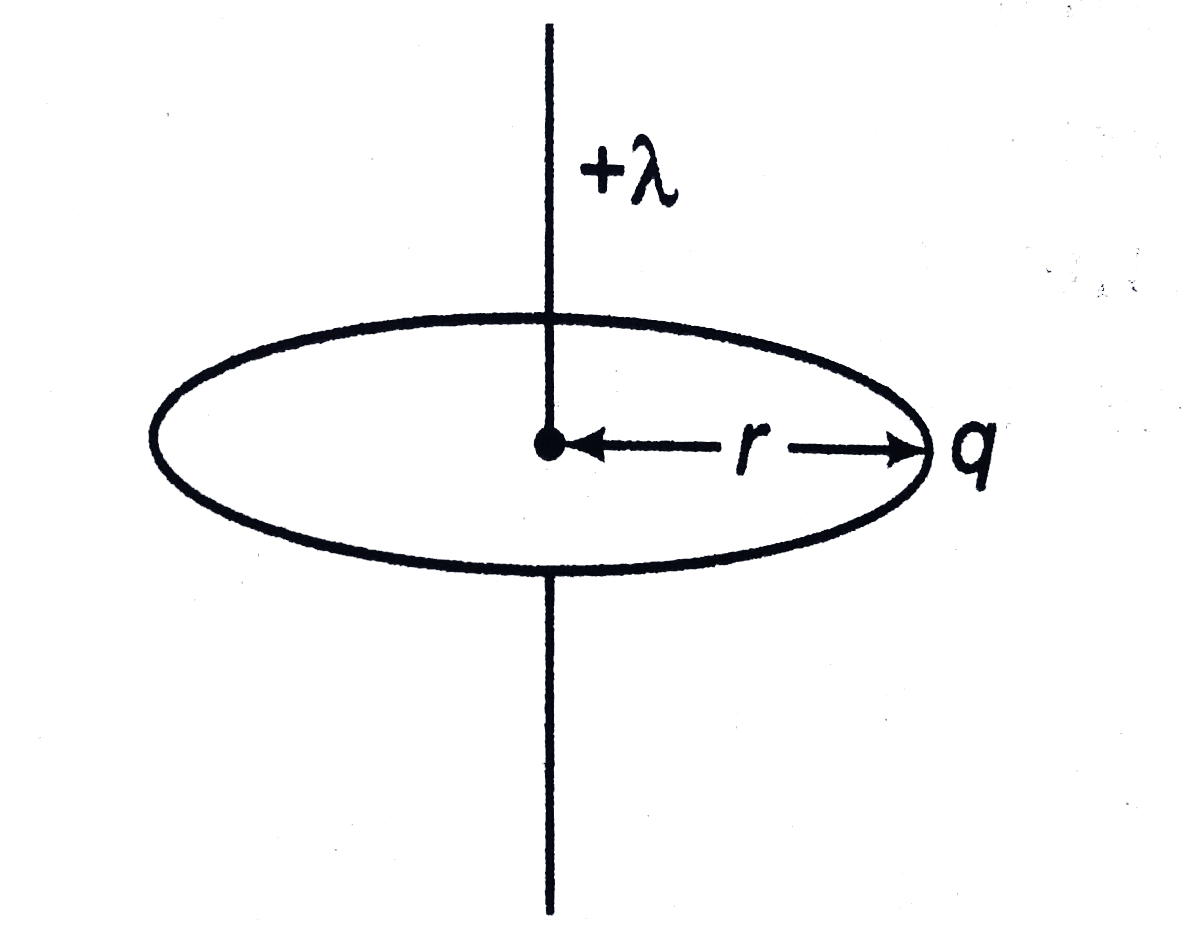
Electric charge is uniformly distributed along a along straight wire of radius `1 mm`. The charge per centimeter length of the wire is `Q` coulomb. Another cyclindrical surface of radius `50 cm` and length `1 m` symmetrically enclose the wire ask shown in figure. The total electric flux passing through the cyclindrical surface is

A copper(density of Cu=`p_(c)`) ball of diameter dis innnersed in oil of density `p_(0)` . What is the charge on the ball if, in a homogeneous elecltric field E directed vertically upward, it is suspended in the oil ?`(k=pid^(3)(p_(c)g)/(E))` :

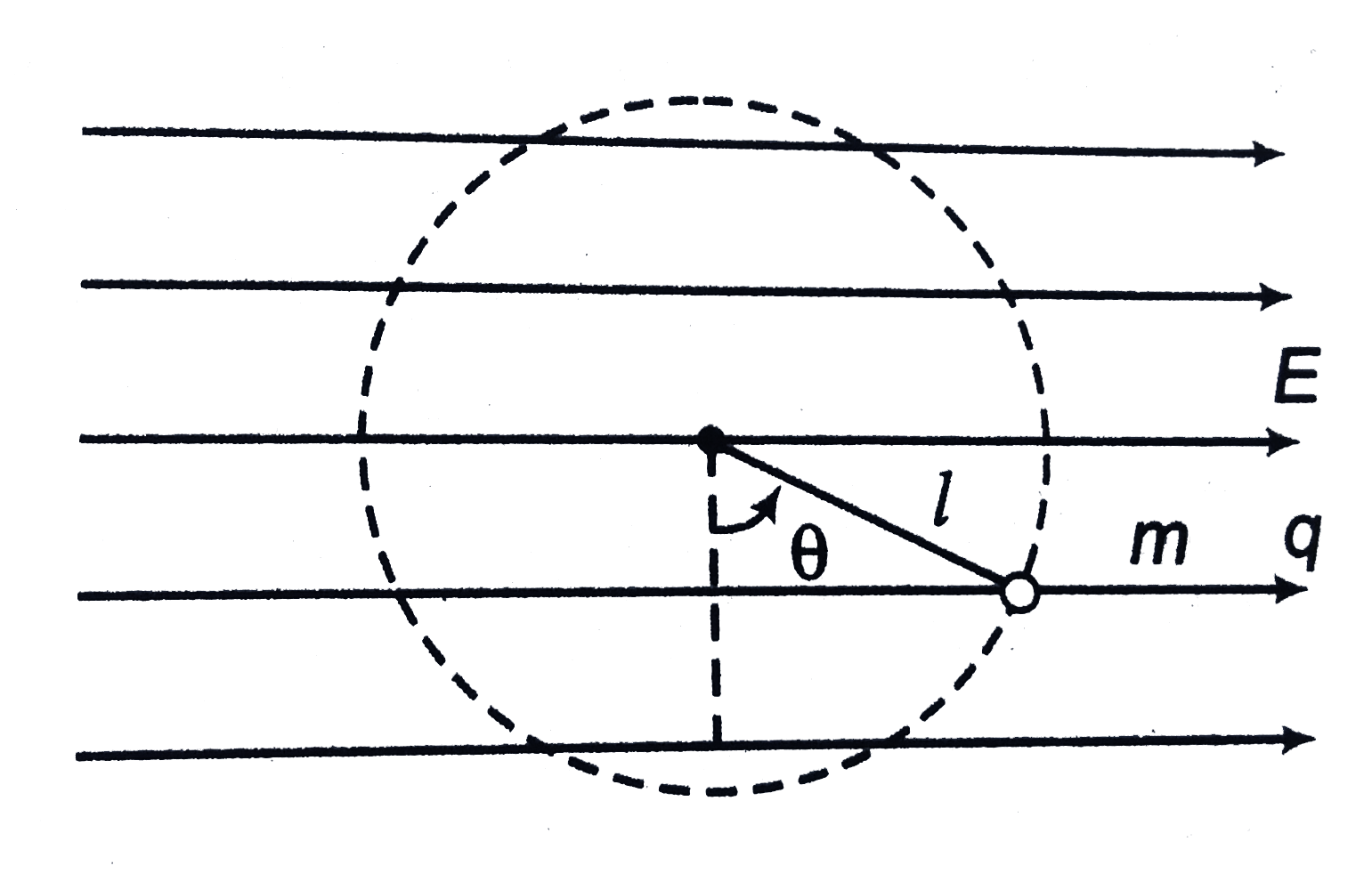
A particle of mass m and charge q is fastened to one end of a string of length. The other end of the string is fixed to the point O. The whole sytem liles on as frictionless horizontal plane. Initially, the mass is at rest at A. A uniform electric field in the direction shown in then switfched on. Then

A small ball of masss m and charge +q tied with a string of length l, rotating in a veticle circle under gravity and a uniform horizontal electric field E as shown. The tension in the string will be minimum for

If unifrom electric filed `vecE = E_(0)hati + 2E_(0) hatj`, where `E_(0)` is a constant, exists in a region of space and at `(0, 0)` the electric potential `V` is zero, then the potential at `(x_(0),0)` will be.

Two metal pieces having a potential difference of `800V` are `0.02 m` apart horizontally. A particle of mass `1.96xx10^(-15) kg` is suspended in equilibrium between the plates. If the `e` is the elementary charge, then charge on the particle is

A sphere of radius 2R has a uniform charge density p. The difference in the electric potential at r = R and r = 0 from the centre is:

A sphere of radius R carries charge density p proportional to the square of the distance from the centre such that `p = Cr^(2)`, where C is a positive constant. At a distance R`//`2 from the centre, the magnitude of the electric field is :

The work done in bringing a `20` coulomb charge from point `A` to point `B` for disatnce `0.2 m` is `2 J`. The potential difference between the two points will be (in volt)

In an electric field region, the electric potential varies along the x-axis as shown in the graph. The `x` components of the electirc field in the regions for the intervals `PQ` and `QR` as market in the garph, in `N//C`, are respectively:

Two spheres A and B of radii 17 cm each and having charges of 1 and 2 coulombs respectively are separated by a distance of SO cm. The electric field at a point on the line joining the centres of two spheres is approximately zero at some distance from the sphere A. The electric potential at this point is:

Electric potential at any point in a region is given as
`V=5x+3y+sqrt15z`
In this region the magnitude of the electric field is:

A charge `+Q` is uniformly distributed in a spherical volume of radius R. A particle of charge `+q` and mass m projected with velocity `v_0` the surface of the sherical volume to its centre inside a smooth tunnel dug across the sphere. The minimum value of `v_0` such tht it just reaches the centre (assume that thee is no resistance on the particle except electrostatic force) of he sphericle volume is

A charge `+q` is fixed at each of the points `x=x_0`, `x=3x_0`, `x=5x_0`,…………`x=oo` on the x axis, and a charge `-q` is fixed at each of the points `x=2x_0`, `x=4x_0`, `x=6x_0`, …………`x=oo`. Here `x_0` is a positive constant. Take the electric potential at a point due to a charge Q at a distance r from it to be `Q//(4piepsilon_0r)`.Then, the potential at the origin due to the above system of

The displacement of a chrage `Q` in the electric field
`E = e_(1)hati + e_(2)hatj + e_(3)hatk " is " vecr = ahati + bhatj`. The work done is

A non-conducting ring ofradius 0.5 m carries a total charge of `1.11xx10^(-10)` C distributed non-uniformly on its circumference producing an electric field `vecE` everywhere in space. The value of the line integral `int_(l=oo)^(l=0)-vecE.dvecl` (l= 0 being centre of the ring) is

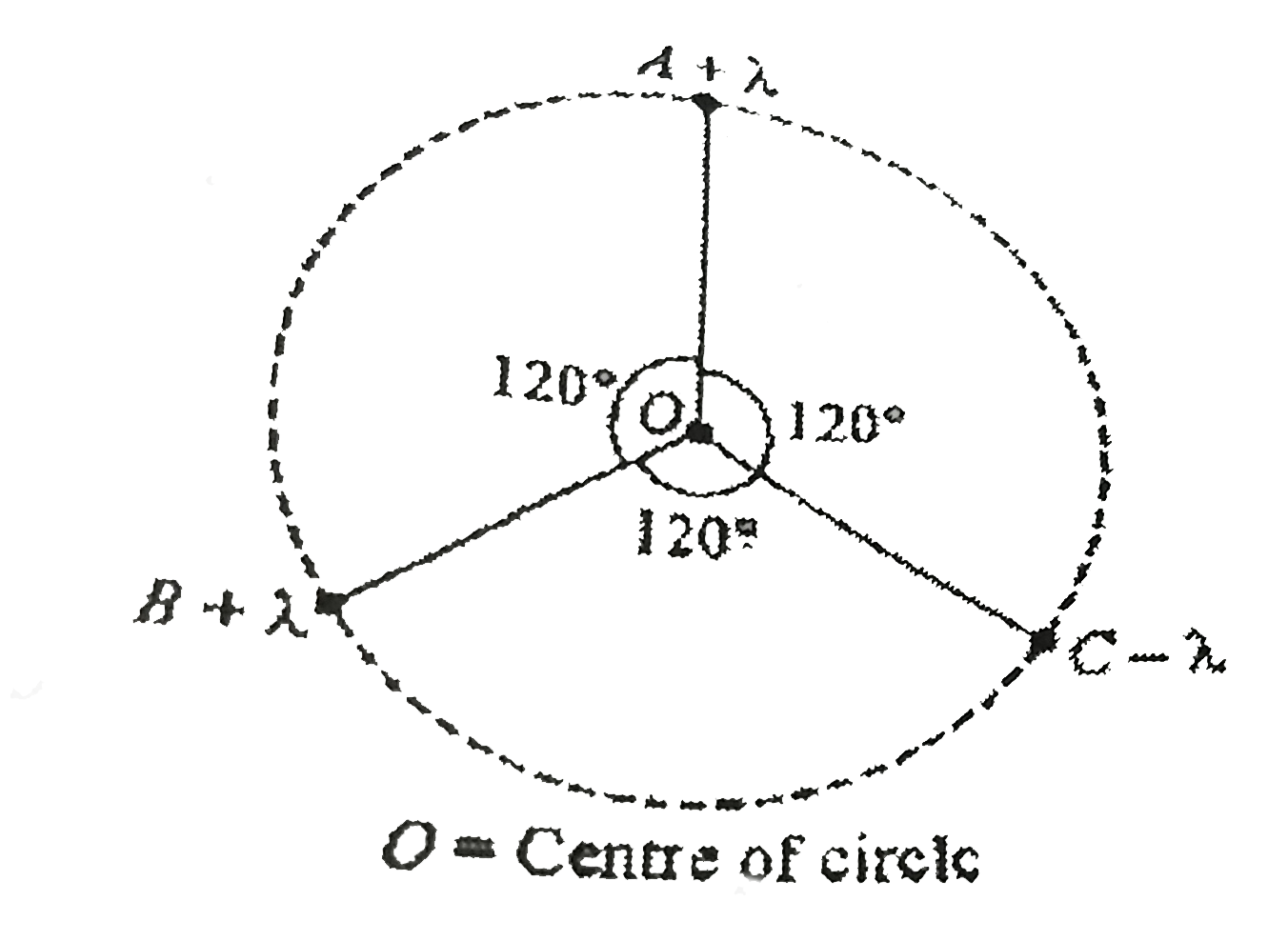
Three semi-infinite rods uniformly charged out of which one is negatively charged and other two are positively charged are kept perpendicular to plane of paper outward such that the finite ends of the rods are located at points A, B and C on a circle of radius R as shown in figure. The net electric field at centre of circle O is :

Two small balls of mass Meach carrying charges `+Q` and `-Q`, connected by a massless rigid non-conducting rod of length L lie along x-axis as shown. A uniform electric field`vecE=3hatk+3hatj` has been switched on. The angular velocity vectorof the dipole when dipole nioment aligns with the electric field is :

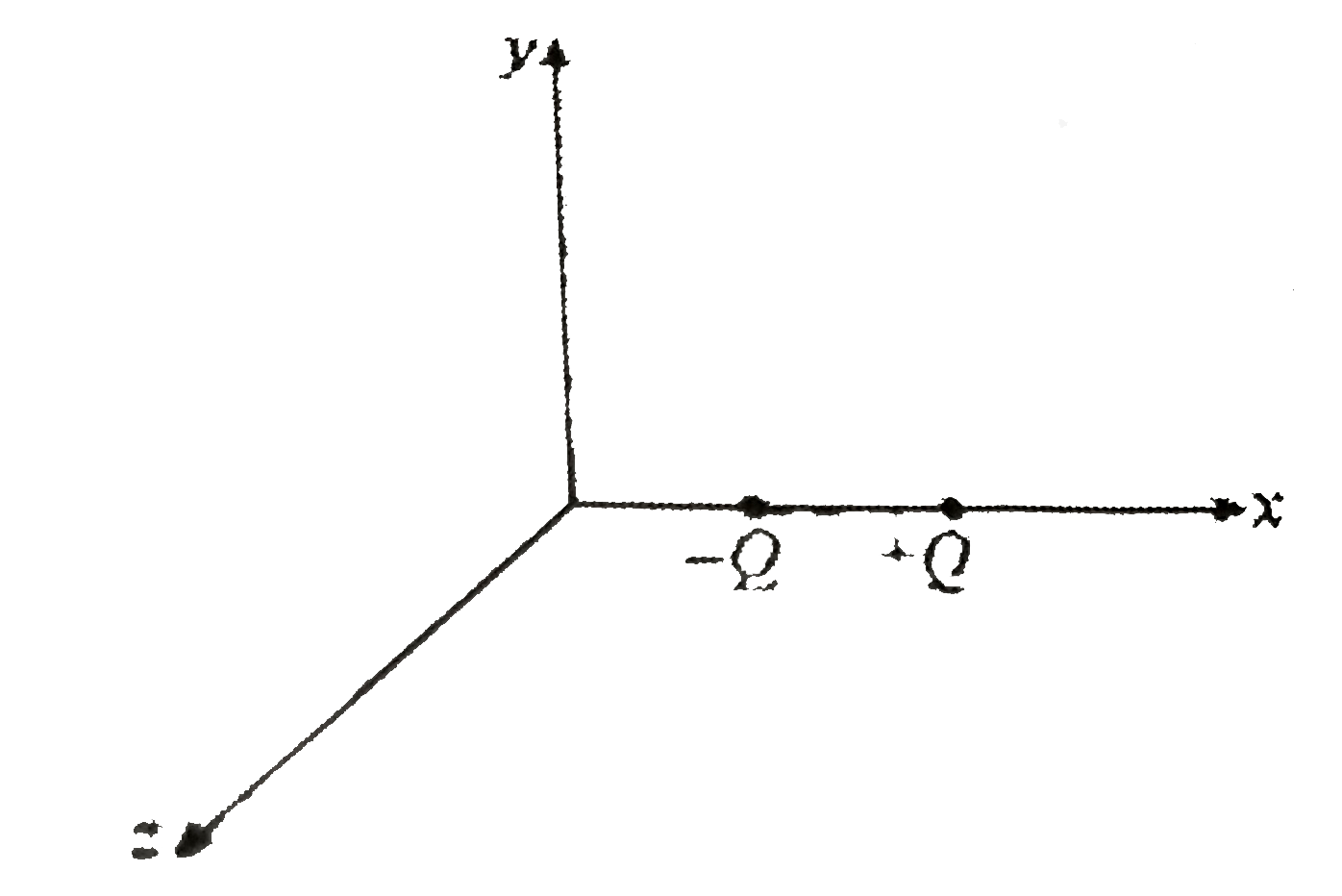
A particle of mass m and charge `-q` is projected from the origin with a horizontal speed v into an electric field of intensity E directed downward. Choose the wrong statement. Neglect gravity

The grid (each square of `1mxx1m`), represents a region in space containing a uniform electric field. If potentials at point O,A,B,C,D,E,F,G,H are respectively 0,-1,-2, 1,2,0,-1, 1 and 0 volts. Find the electric field intensity :

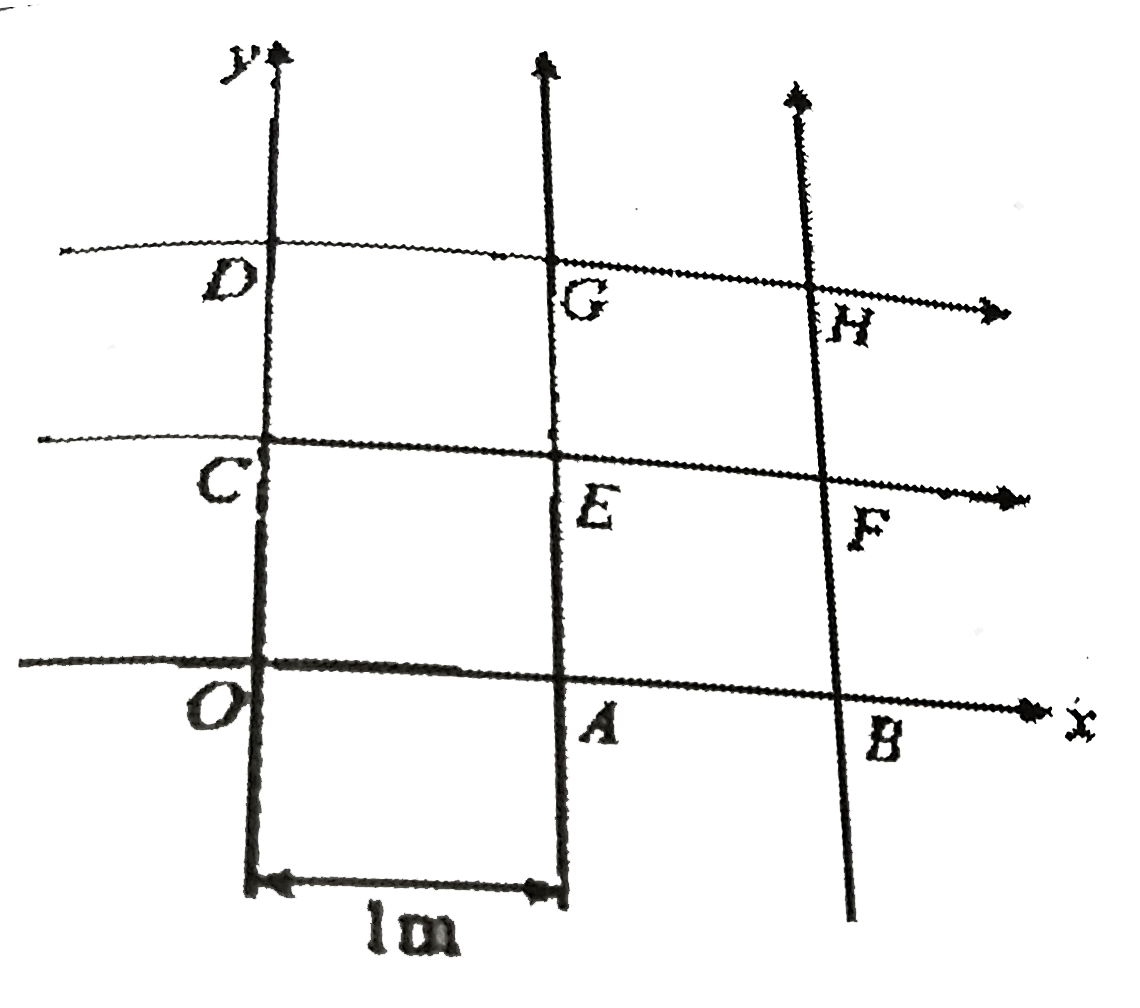
At a certain distance from a point charge, the field intensity is `500 V//m` and the potentil is `-3000 V`. The distance to the charge and the magnitude of the charge respectively are

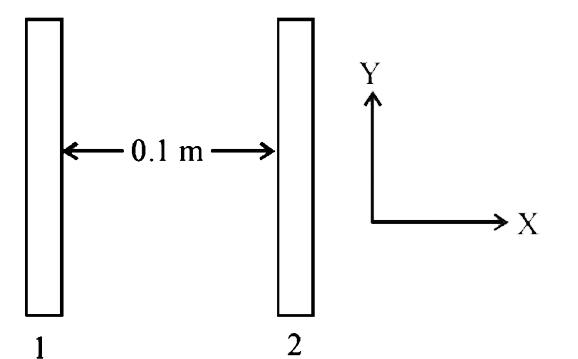
Two insulting plates are both uniformly charged in such a way that the potential difference between them is `V_2-V_1=20V`. (i.e., plate 2 is at a higher potential). The plates are separated by `d=0.1m` and can be treated as infinity large. An electron is released from rest on the inner surface of plate 1. What is its speed when it hits plate 2? (`e=1.6xx10^-19C`, `m_e=9.11xx10^-31kg`)

Q charge is uniformaly distributed over the same surface of a right circular cone of semi -vertical angle theta and height h The cone is uniformly rotated about its axis at angular velocity omega Calculated associated magnetic dipole moment
.

A conducting rod of length I rotates about its one end with angolar velocity ro. Potential difference between A and B points ofrod as shown in figore `-1.404 is V AB" Find VAB"` Taken as mass of electron and e is the charge of electron :

A tiny spherical oil drop carrying a net charge q is balanced in still air with a vertical uniform electric field of strength `(81pi)/(7)xx10^5Vm^-1`. When the field is switched off, the drop is observed to fall with terminal velocity `2xx10^-3ms^-1`. Given `g=9.8ms^-2`, viscoisty of the air `=1.8xx10^-5Nsm^-2` and the denisty of oil `=900kg m^-3`, the magnitude of q is

The two ends of a rubber string of negligible mass and having unstretched length 24cm are fixed at the same height as shown. A small object is attached to the string in its midpoint due to which the depression h of the object in equilibrium is 5cm. Then the small object is charged and a vertical electric field `E_(1)` is switched on in the region. The ·equilibrium depression of the object increases to 9cm, now the electric field is changed to `E_(2)` and the depression of object in equilibrium increases to 16cm. What is the ratio of electric field in the second case to that of in the first case ?

Let there be a spherically symmetric charge distribution with charge density varying as `rho(r)=rho(5/4-r/R)` upto `r=R`, and `rho(r)=0` for `rgtR`, where r is the distance from the origin. The electric field at a distance r(rltR) from the origin is given by

The ratio of the electric force between two electrons to the gravitational force between them is of the order of

Two points charges `q_1 and q_2` are placed at a distance of 50 m from each each other in air, and interact with a certain force. The same charges are now put in oil whose relative permittivity is 5. If the interacting force between them is still the same, their separation now is

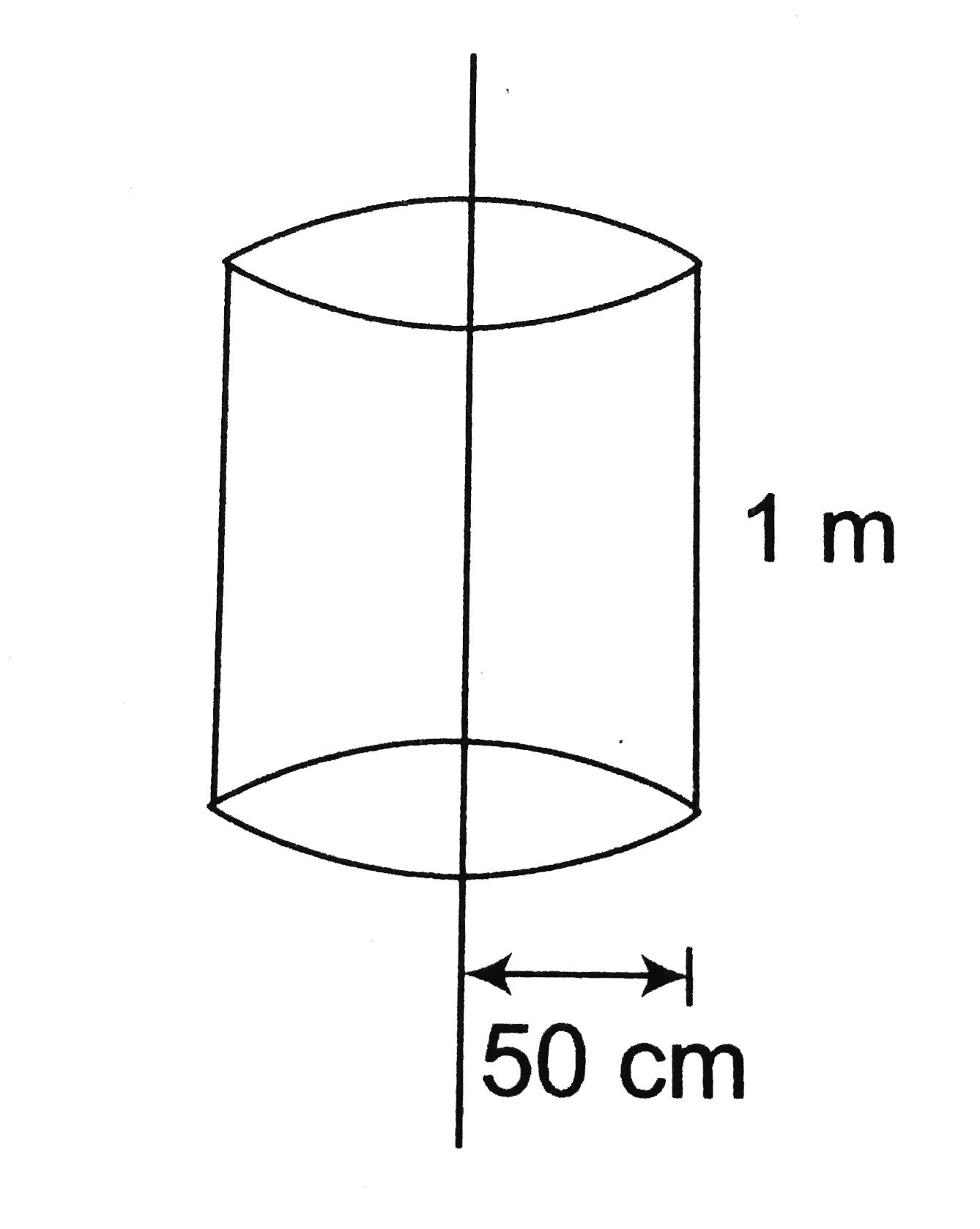
An electric field is uniform, and in the positive x-direction for positive x, and uniform with the same magnitude , but in the negative x-direction for negative x. It is given that
`vec(E) = 200 hat(i) N//C for x gt 0 and vec(E) = -200 hat(i) N//C` for x gt 0. A right circular cylinder of length 20 cm and raidus 5cm has its center at the origin and its axis along the x-axis so that one face is at `x = +10 cm` and the other is at `x = -10 cm`.
(a) What is the net outward flux through the side of the cylinder ? (b) What is the net outward flux through the cyclinder ? (c) what is net charge inside the cylinder ?

A solid conducting sphere ofradius 5.0 cm has a charge of 0.25nC distributed uniformly on its surface. If point A is located at the centre of the sphere and a point Bis 15cm from the center, what is the magnitude of the electric potential difference between these two points ?

An electric dipole is placed perpendicular to an infinite line of charge at same distance as shown in figure. Identify the correct statement.

S is a solid neutral conducting sphere. A point charge q of 1 × 10–6 C is placed at point A. C is the centre of sphere and AB is a tangent. BC = 3m and AB = 4m.
(1) The electric potential of the conductor is 1.8 kV
(2) The electric potential of the conductor is 2.25 kV
(3) The electric potential at B due to induced charges on the sphere is – 0.45 kV
(4) The electric potential at B due to induced charges on the sphere is 0.45 kV

If the potential at the centre of a uniformly charged hollow sphere of radus R is V, then electric field at a distance r from the centre of sphere will be `(rgtR)`.

An isolated conduction sphere sphere whose radius `R=1` m has a charge `q=1/9nC.` The energy density at the surfasce of the sphere is

A charged rod have continuous charge distribution having density ` lamda= 2x C//m`. If rod is of length l then find ratio `(q_(1))/(q_(2))`. where `q_(1)` is charge on half ofrod & `q_(2)` is charge on `2^(nd)` half of rod"

Three concentric spherical metallic shells A, B and C of radii a, b and c (a lt b ltc) have surface charge densities `sigma`, `-sigma` and `sigma` respectively.
`(i) Find the potential of the three shells A, B and C.
(ii) If the shells A and C are at the same potential, obtain the relation between the radii a, b and c.

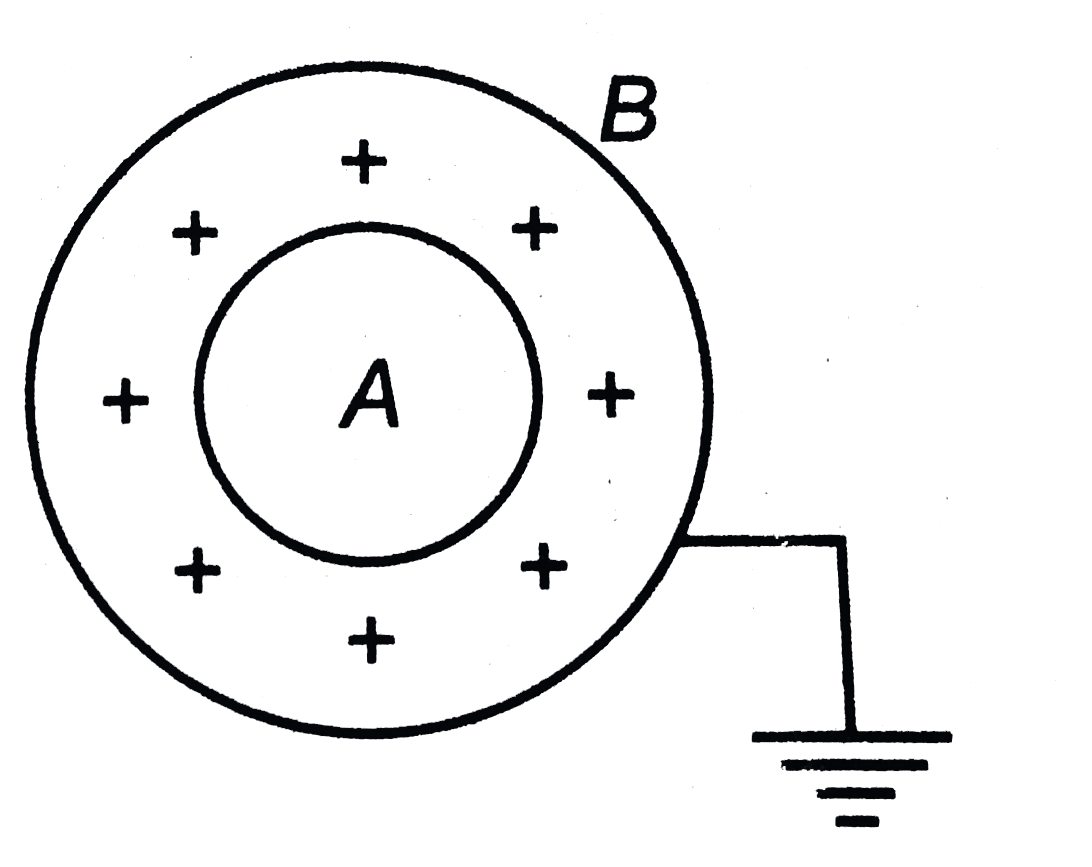
A and B are two concentric spherical shells. If A is given a charge `+q` while B is earthed as shown in figure then

The electrostatic potential due to the charge configuration at point P as shown in figure for bltlta is

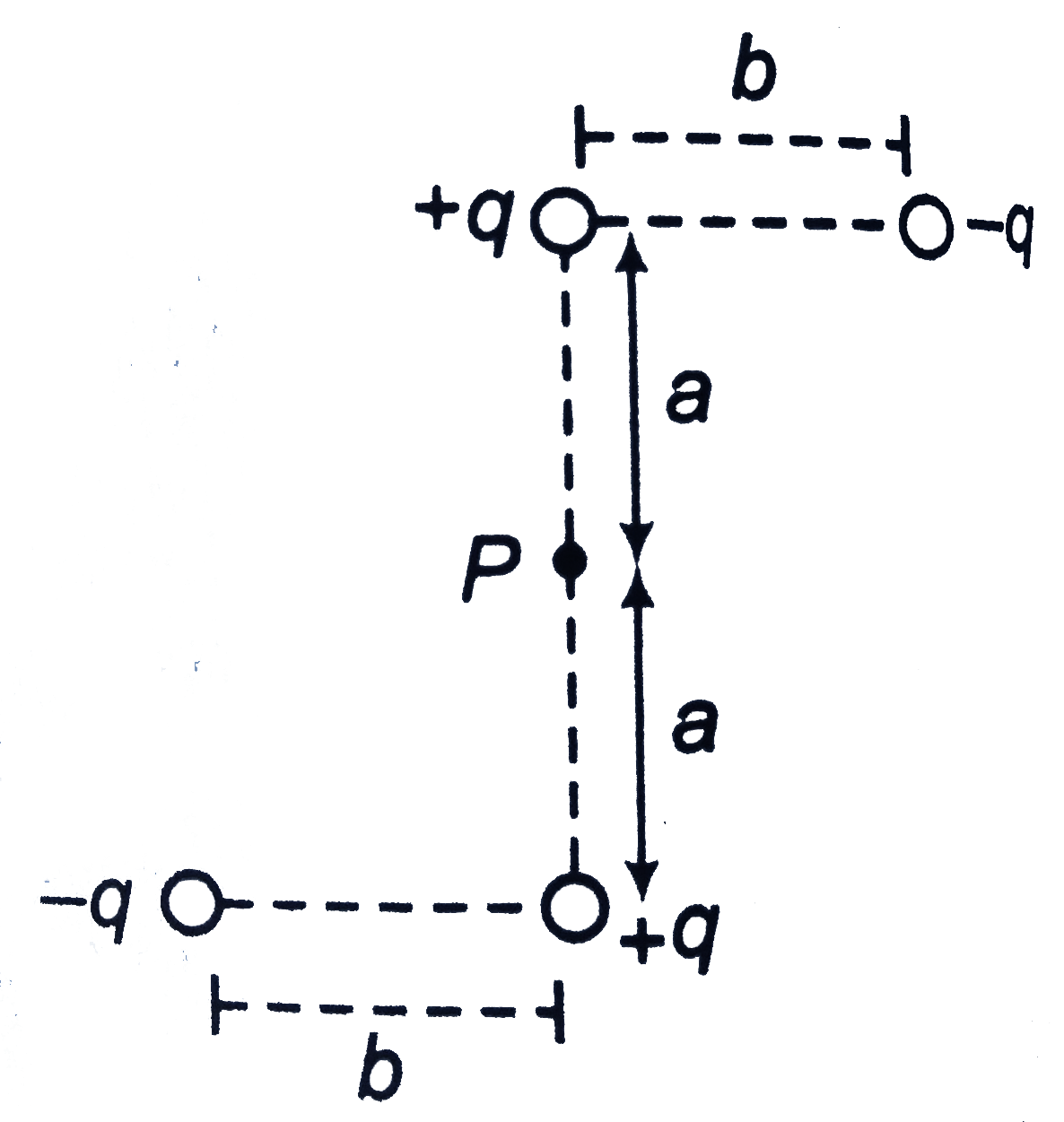
Two thin wire rings each having radius R are placed at distance d apart with their axes coinciding. The charges on the two are `+Q` and `-Q`. The potential difference between the centre so the two rings is

In a certain region of space, electric field is along the z-direction throughout. The magnitude of electric field is , however, not constant but increases uniformly along the positive z-direction. At the rate of `10^(5)NC^(-1)m^(-1)` . What are the force and torque experienced by system having a total dipole moment equal to `10^(-7)`Cm in the negative z-direction?

There are two uncharged identicasl metallic spheres 1 and 2 of radius r separated by a distance `d(dgtgtr)`. A charged metalllic sphere of same radius having charge q is touched with one of the sphere. After some time it is moved away fom the system. Now, the uncharged sphere is earthed. Charge on earthed sphere is

Two small identical metal balls of radius rare at a distance a `(a lt lt r)` from each other and are charged, one with a potential `V_(1)` and the other with a potential `V_(2)`. The charges on the balls are:

In the diagram shown the charge `+Q` is fixed. Another charge `+2q` and mass M is projected from a distance R from the fixed charge. Minimum separtion between the two charge if the velocity becomes `1/sqrt3` time of the projected velocity, at this moment is (Assume gravity to be absent)

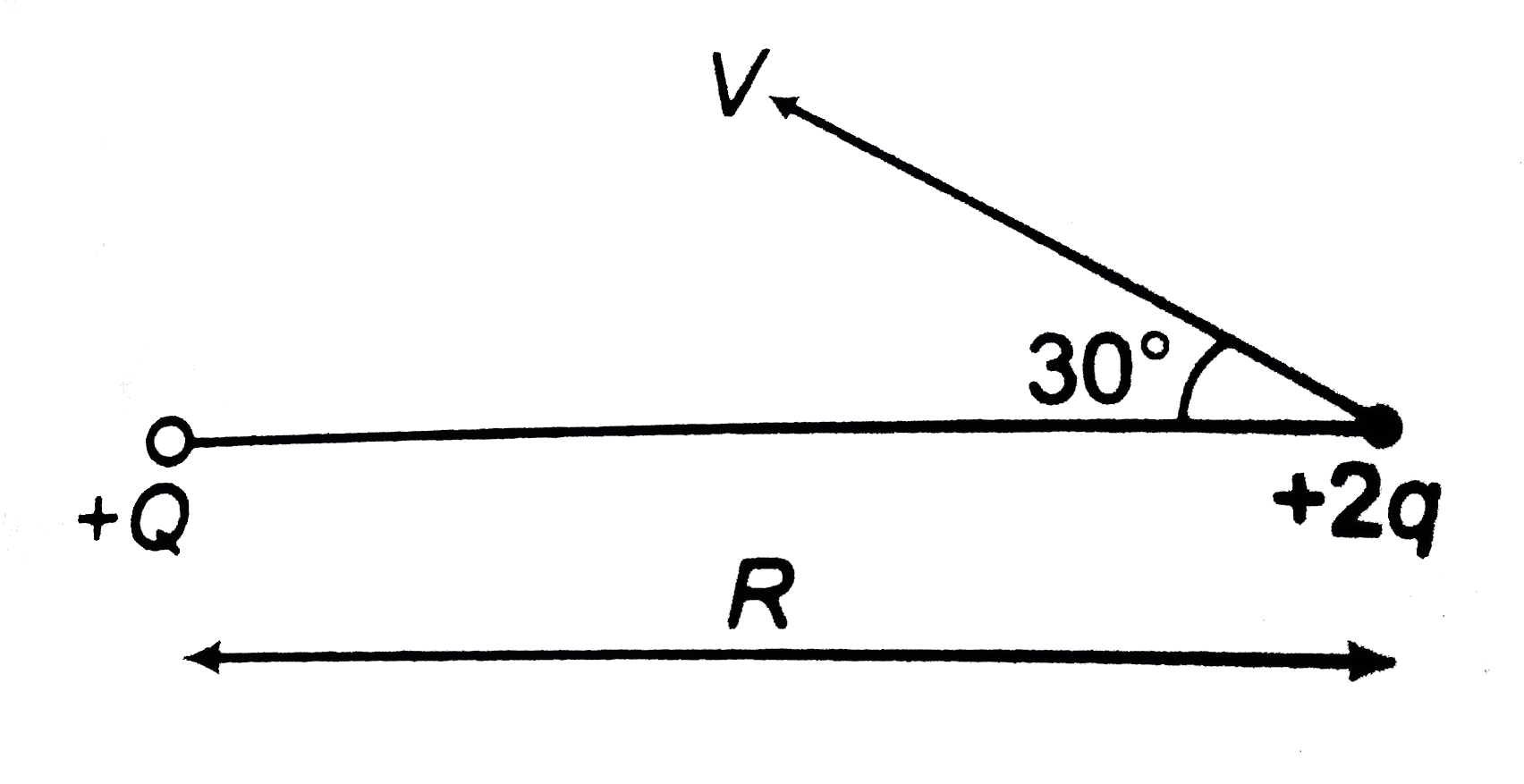
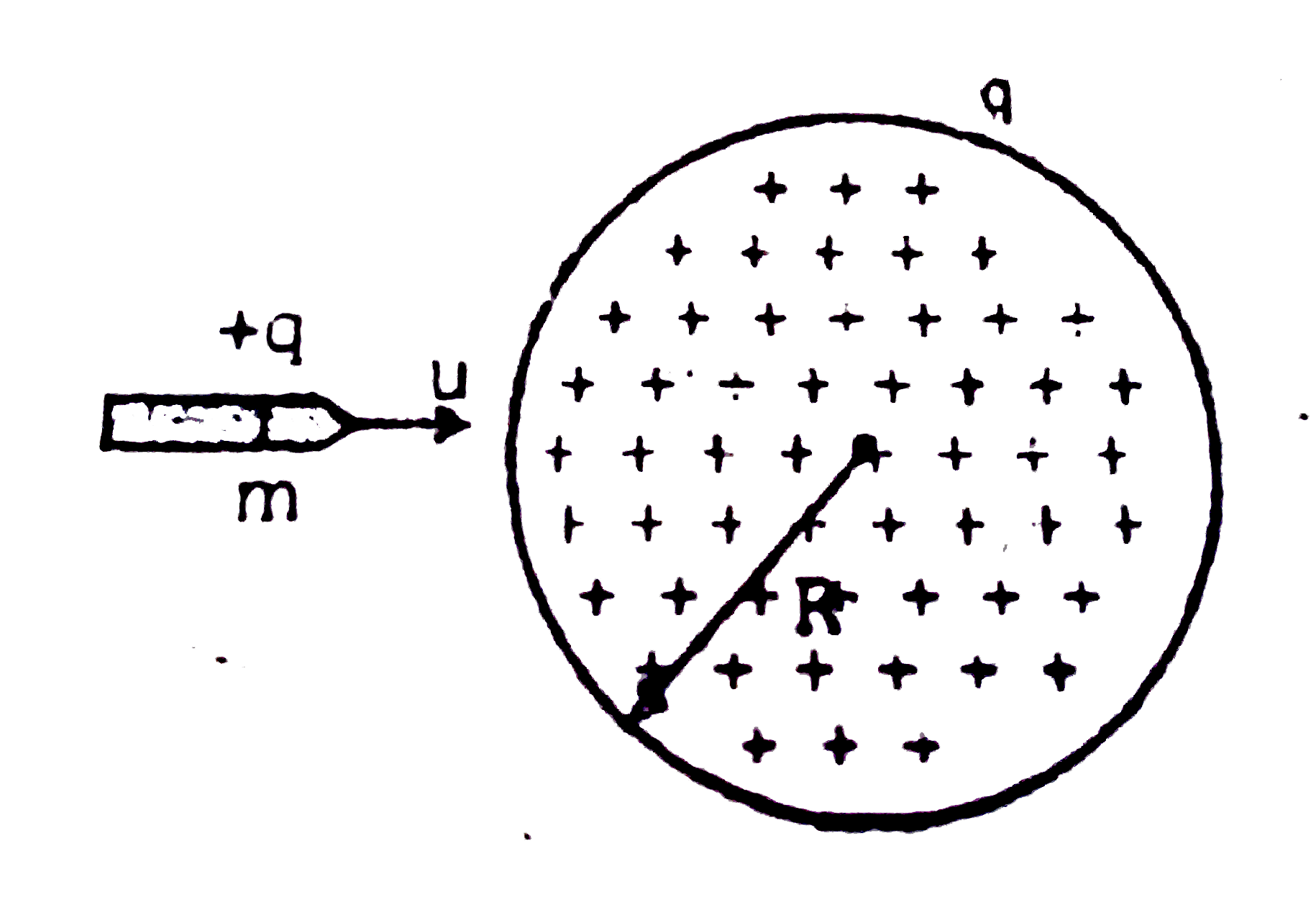
A bullet of mass m and charge q is fired towards a solid uniformly charge sphere of radius R and total charge +q. If it strikes the surface of sphere with speed u, find the minimum value of u so that it can penetrate through the sphere. (Neglect all resistance force or friction acting on bullet except electrostatic forces)

A charged particle of mass `m` and charge `q` is released from rest in an electric field of constant magnitude `E`. The kinetic energy of the particle after time `t` is

Consider the shown uniform solid insulating sphere of mass m with a short and light electric dipole moment `p hat(j)` embedded at its centre placed at rest on a horizontal surface. An electric field `E hat(i)` is suddenly switched on in the region such that the sphere starts ro/ling without sliding. Speed of the sphere when the dipole becomes horizontal for the first time is given as:

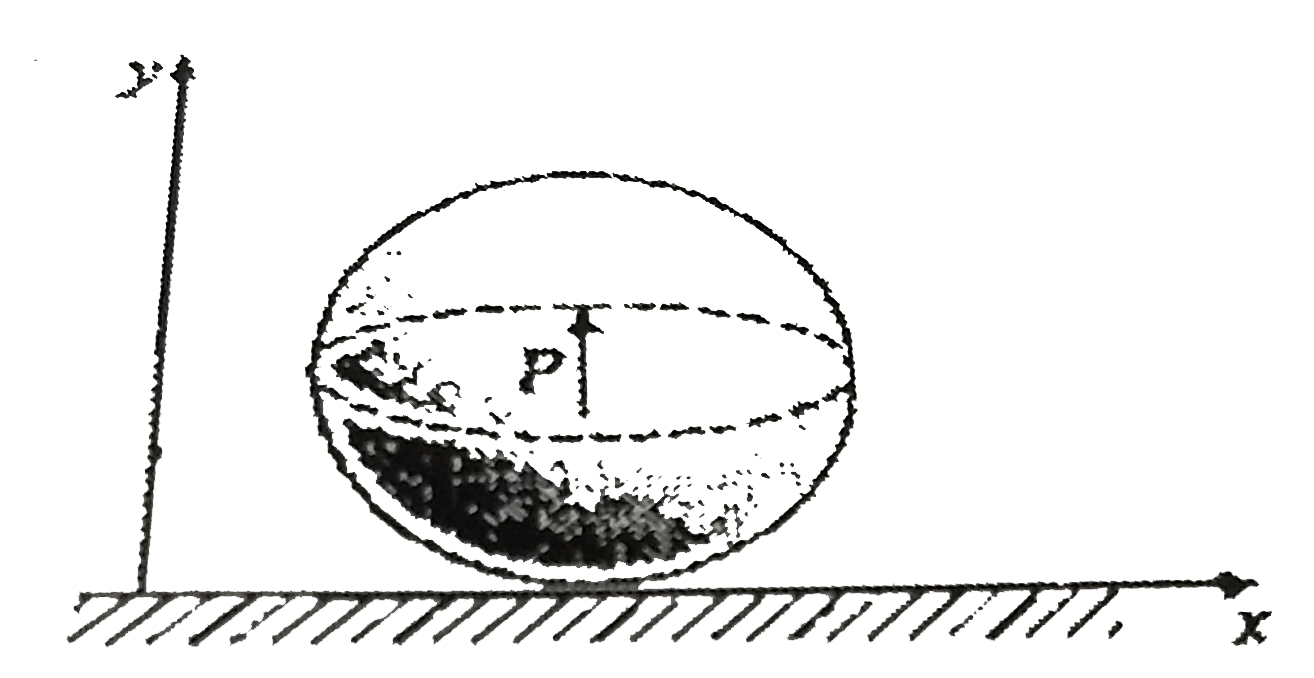
A ring of diameter d is rotated in a uniform electric field until the position of maximum electric flux is found. The flux is found to be `phi`. What is the electric field strength?

A block of mass m and charge q is connected to a point 0 with help ofan inextensible string. The system in on a horizontal table. An electric field is switched on in direction perpendicular to string. What will be tension in string when it become parallel to electric field?

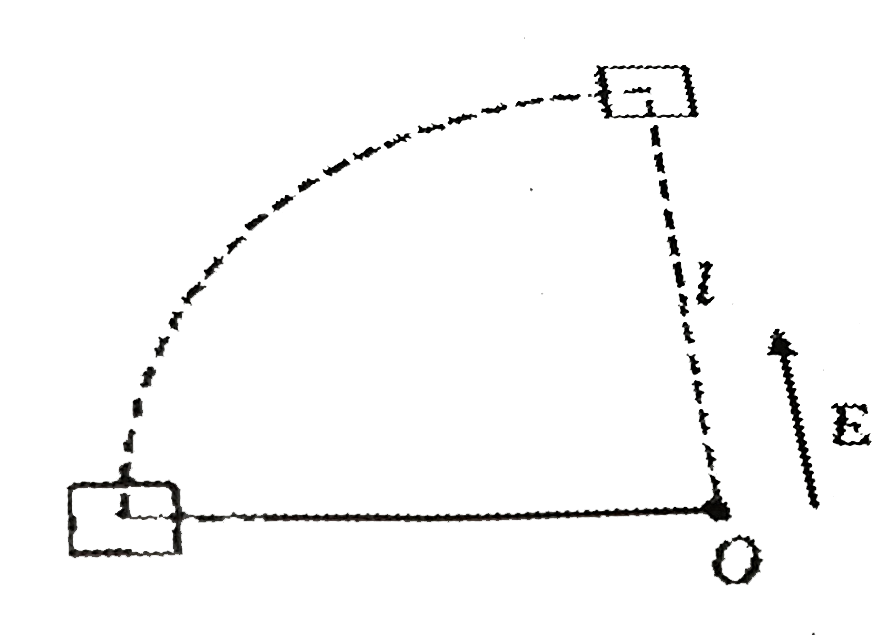
The electric potential `V` at any point `(x,y,z)`, all in meters in space is given by `V= 4x^(2)` volt. The electric field at the point `(1,0,2)` in volt//meter is

A solid sphere having uniform charge density `rho` and radius R is shown in figure. A spherical cavity ofradius `(R)/(2)` is made in it. What is the potential at point O?

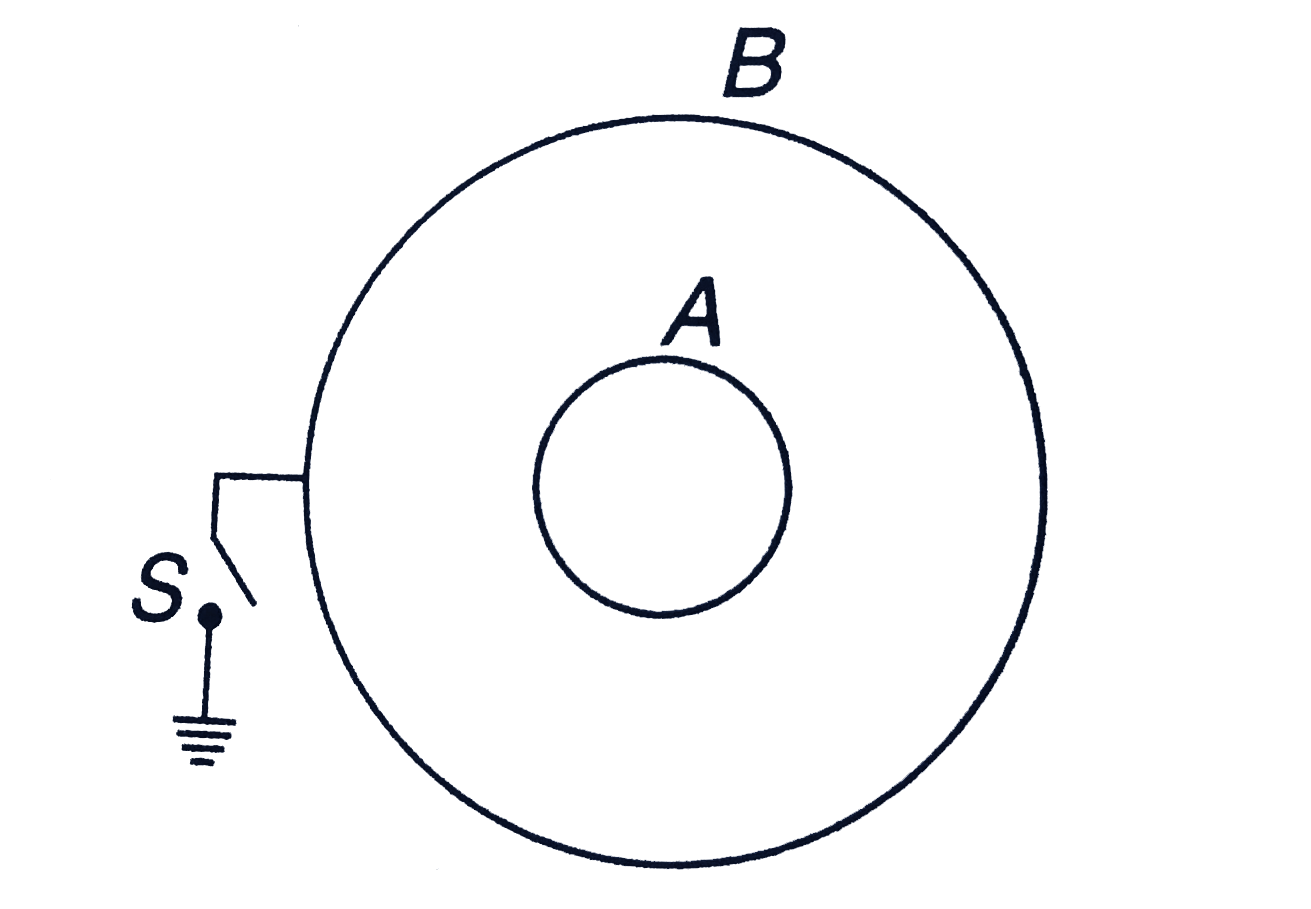
Initially the spheres A and B are at potentials `V_A` and `V_B`. Find the potential of A when sphere B is earthed.

A charge q is placed at the centre of the line joining two equal charges Q. The system of the three charges will be in equilibrium if q is equal to:

A thin non-conducting ring or radius a has a linear charge density `lambda = lambda_(0) sin phi`. A uniform electric field `E_(0) hat(i) + E_(0) hat(j)` exist in the region . .Net torque acting on ring is given as :

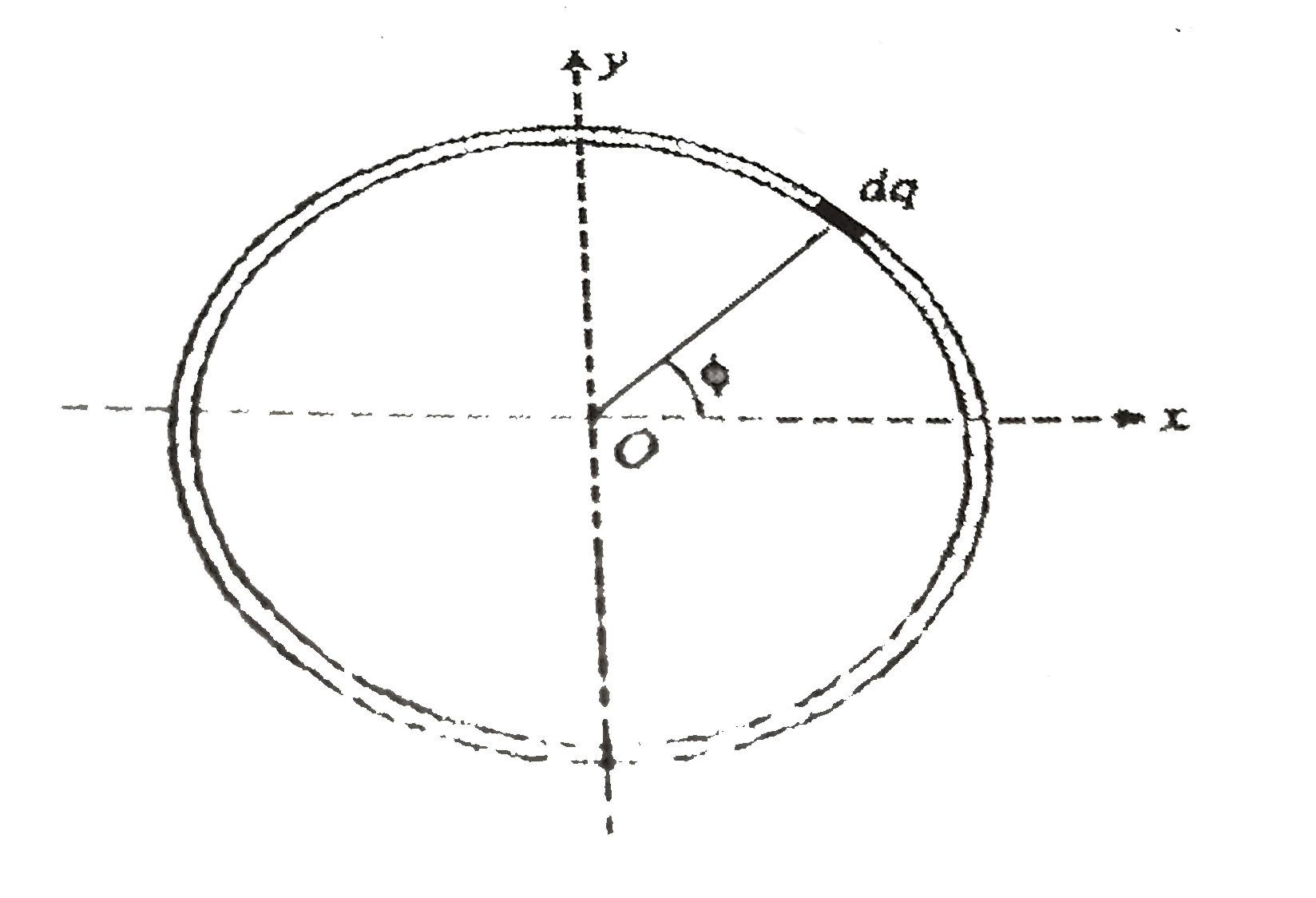
The locus of the points (in the `xy`-plane) where the electric field due to a dipole (dipole axis is along `x`-axis and its equatorial is along `y`-axis) is perpendicular to its axis, is

A ring of radius `R` having a linear charge density `lambda` moves towards a solid imaginary sphere of radius `(R)/(2)`, so that the centre of ring passes through the centre of sphere. The axis of the ring is perpendicular to the line joining the centres of the ring and the sphere. The maximum flux through the sphere in this process is

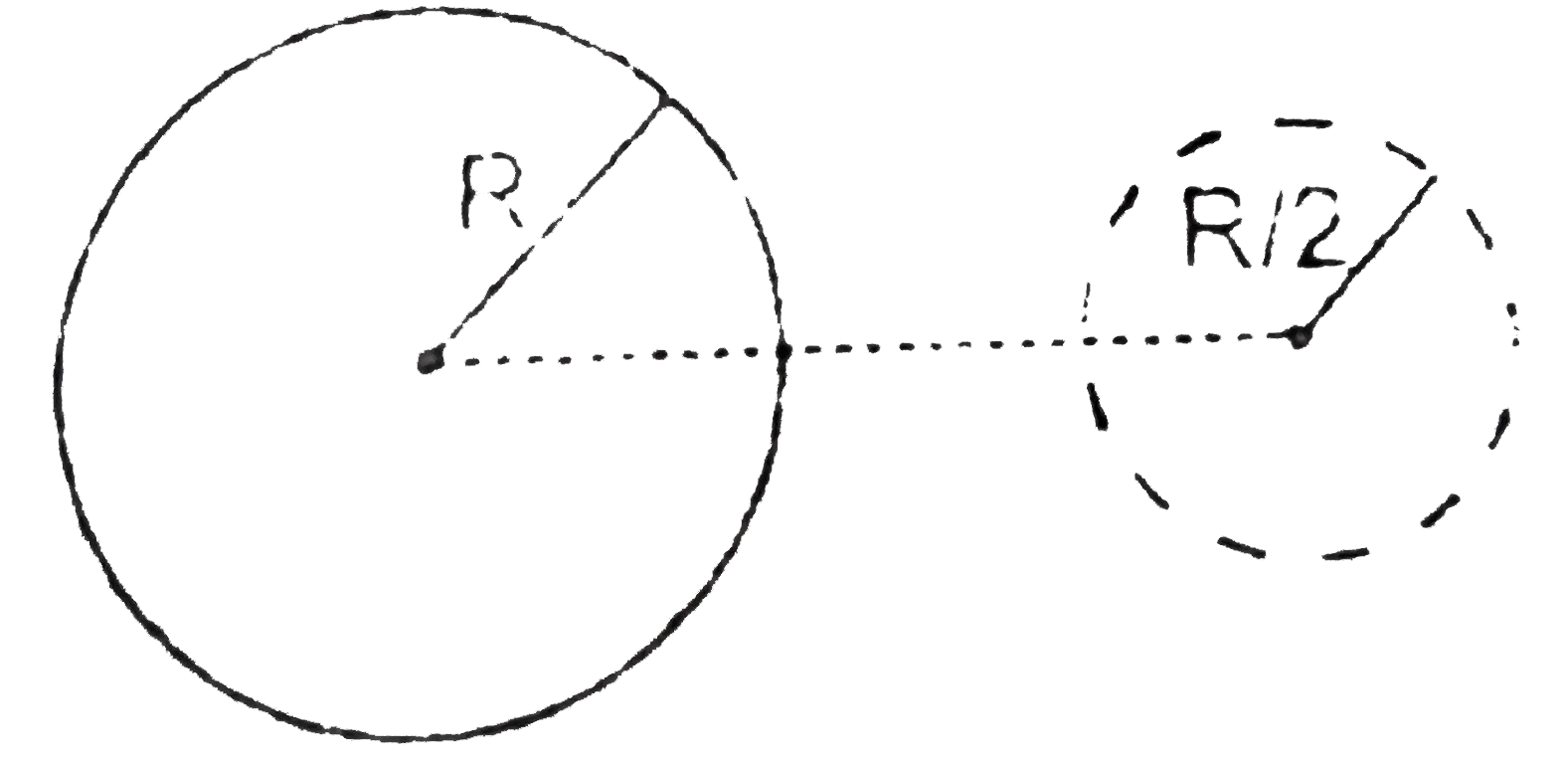
A semi-infinite insulating rod has linear charge density `lambda`. The electric field atthe pointPshown in figure-1.418 is:

Two spherical conductors B and C having equal radii and cayying equal charges on them repel each other with a force F when kept apart at some distance. A third spherical conductor having same radius as that B but uncharged is brought in contact with B, then brought in contact with C and finally removed away from both. The new force of repulsion between B and C is

Two insulated charged spheres of radii `20 cm` and `25 cm` respectively and having an equal charge `Q` are connected by a copper wire, they are separated

A uniform electric field of strength E exists in region. A electron enters a point A with velocity v as shown. It moves through the electric field and reaches at point B. Velocity particle at B is `2v` at `30^@` with x-axis .
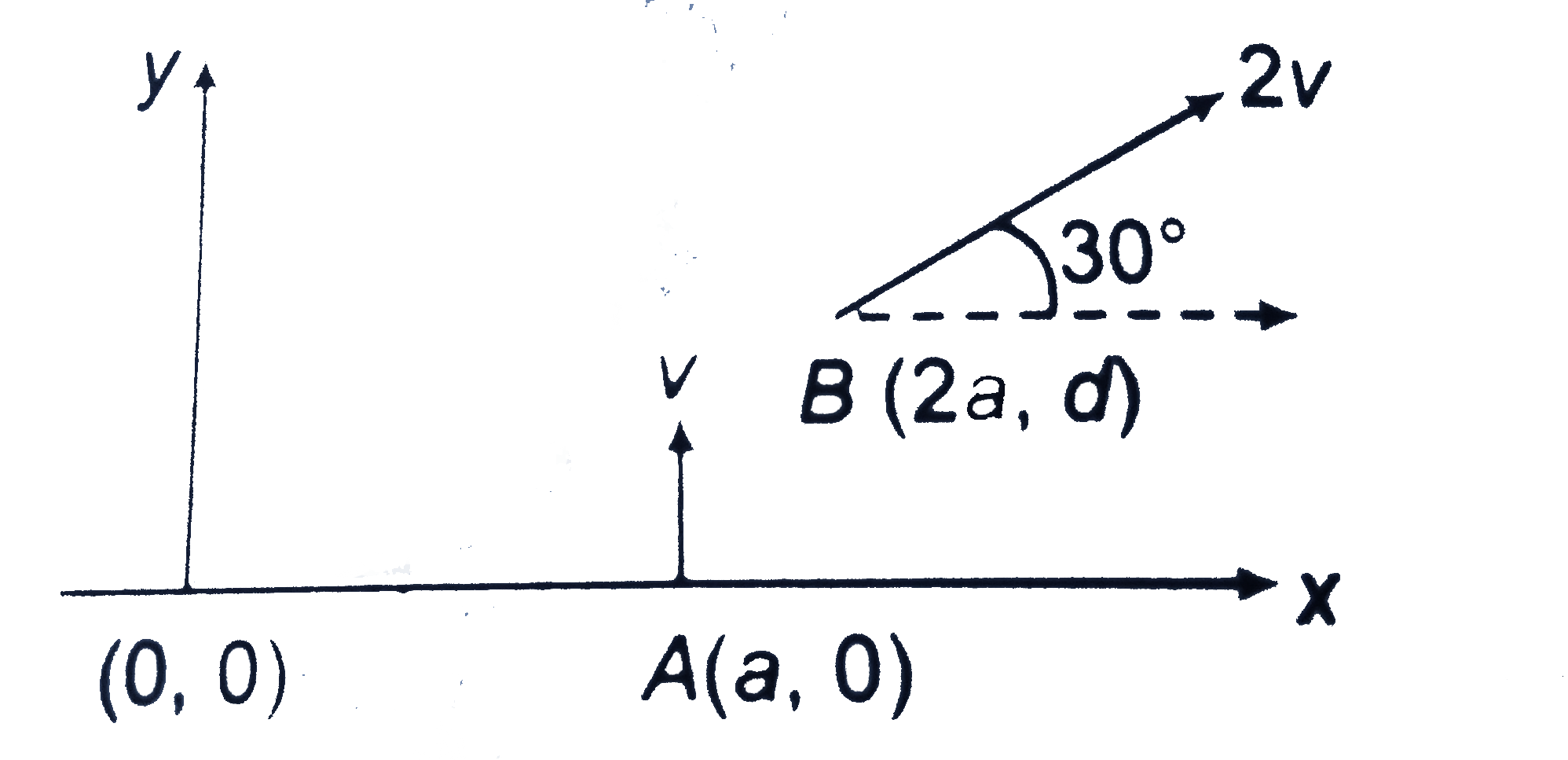
Then

The potential at a point x ( measured in `mu` m) due to some charges situated on the x-axis is given by
`V(x)=20//(x^2-4) vol t`

Four charges `+q, -1, +q` and `-q` are placed in order on the four consecutive corners of a square of side a. The work done in interchanging the positions of any two neighbouring charges of the opposite sign is

A particle of mass m and charge `+q` approaches from a very large distance towards a uniformly charged ring ofradius Rand charge, mass same as that of particle, with initial velocity `v_(0)` along the axis of the ring as shown in the figure-1.420. What is the closest distance of approach between the ring and the particle? Assume the space to be gravity free and frictionless :