Complete Solutions to ILLUSTRATIVE EXAMPLE of chapter HEAT AND THERMAL EXPANSION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | HEAT AND THERMAL EXPANSION |
| PHYSICS GALAXY | ILLUSTRATIVE EXAMPLE |
| Number Of Questions | 30 |
| Academic Year | 2023-24 |
What will be the following temperatures on the kelvin scale: a. `37^@`, b. `80^@F`, c. `-196^@C`?
View SolutionTypical temperatures in the interior of the earth and sum are about `4xx10^(3).^(@)C` and `1.5xx10^(7).^(@)C` respectively.a. What are these temperature in Kelvins? B. What percentage error is made in each case if a person fogets to change `.^(@)C` to K?
View SolutionIn an aluminium there is a hole of diameter 2 m and is horozontally mounted on a stand. Onto this hole an iron sphere of diameter 2.004 m is resting. Initial temperature of this system is `25^(@)C`. Find at what temperature the iron sphere will fall down through the hole in sheet. The coefficient of linear expansion for aluminium and iron are `2.4xx10^(-5)` and `1.2xx10^(-5)` respectively.
View SolutionA metal rod (A) of `25 cm` length expands by `0.050 cm` when its temperature is raised from `0^@ C` to `100^@ C`. Another rod (B) of a different metal of length `40 cm` expands by `0.040 cm` for the same rise in temperature. A third rod ( C) of `50 cm` length is made up of pieces of rods (A) and (B) placed end to end expands by `0.03 cm` on heating from `0^@ C` to `50^@ C`. Find the lengths of each portion of the composite rod.
View SolutionTwo straight thin bars, one of brass and the other of steel are joined togethre side by side by short steel cross-pieces at `0^(@)C`, one cm long the centre lines of the bars being one cm apart. When heated to `100^(@)C`, the composite bar becomes bent into the arc of a circle. calculate the radius of this circle.
`alpha` for brass `=19xx10^(-6)` per `.^(@)C`
and `alpha` for steel `=11xx10^(-6)` per `.^(@)C`
View SolutionA clock with a metallic pendulum gains 5 s each day at a temperature of `15^@C` and loses 10 s each day at a temperature of `30^@C`. Find the coefficient of thermal expansion of the pendulum metal.
View SolutionWhat should be the length of steel and copper rods at `0^(@)C` that the length of steel rod is 5 cm longer than copper at all termperature? Given `alpha_(Cu) = 1.7 xx 10^(5) .^(@)C^(-1)` and `alpha_(steel) = 1.1 xx 10^(5) .^(@)C^(-1)`.
View SolutionA steel wire of corss sectional area `0.5mm^(2)` is held between two rigid clamps so that it is just taut at `20^(@)C`. Find the tension in the wire at `0^(@)C`. Given that Young's Modulus of steel is `Y_(st)=2.1xx10^(12)` dynes/`cm^(2)` and coefficient of linear expansion of steel is `alpha_(st)=1.1xx10^(-5).^(@)C^(-1)`
View SolutionThree rods A,B and C having indentical shape and size, are hingerd together at ends to form an equilateral triangle. Rods A and B are made of same material having coefficient of linea thermal expansion `alpha_(1)` while that of material of rod C is `alpha_(2)`. By how many kelvin should the system of rods be heated to increase the angle opposite to rod C by `Delta theta`.
View SolutionA pendulum clock and a digitical clock both are synchronized to beep correct time at temperature `20^(@)C` in the mornign on 1st March, 2003. At 12:00 noon temperature increases to `40^(@)C` and remains constant for three months. Now on Ist June, 2003 at 12:00 noon temperature drops to `10^(@)C` and remains constant for a very long duration. Find the date and time on which both the clocks will again be synchronized for a moment.
View SolutionAt room temperature (`25^@C`) the length of a steel rod is measured using a brass centimetre scale. The measured length is 20 cm. If the scale is calibrated to read accurately at temperature `0^@C`, find the actual length of steel rod at room temperature.
View SolutionA rod AB of length l is pivoted at an end A and freely rotated in a horizontal plane at an angular speed `omega` about a vertical axis passing through A. If coefficient of linear expansion of material of rod is `alpha`, find the percentage change in its angular velocity if temperature of system is incresed by `DeltaT`
View Solution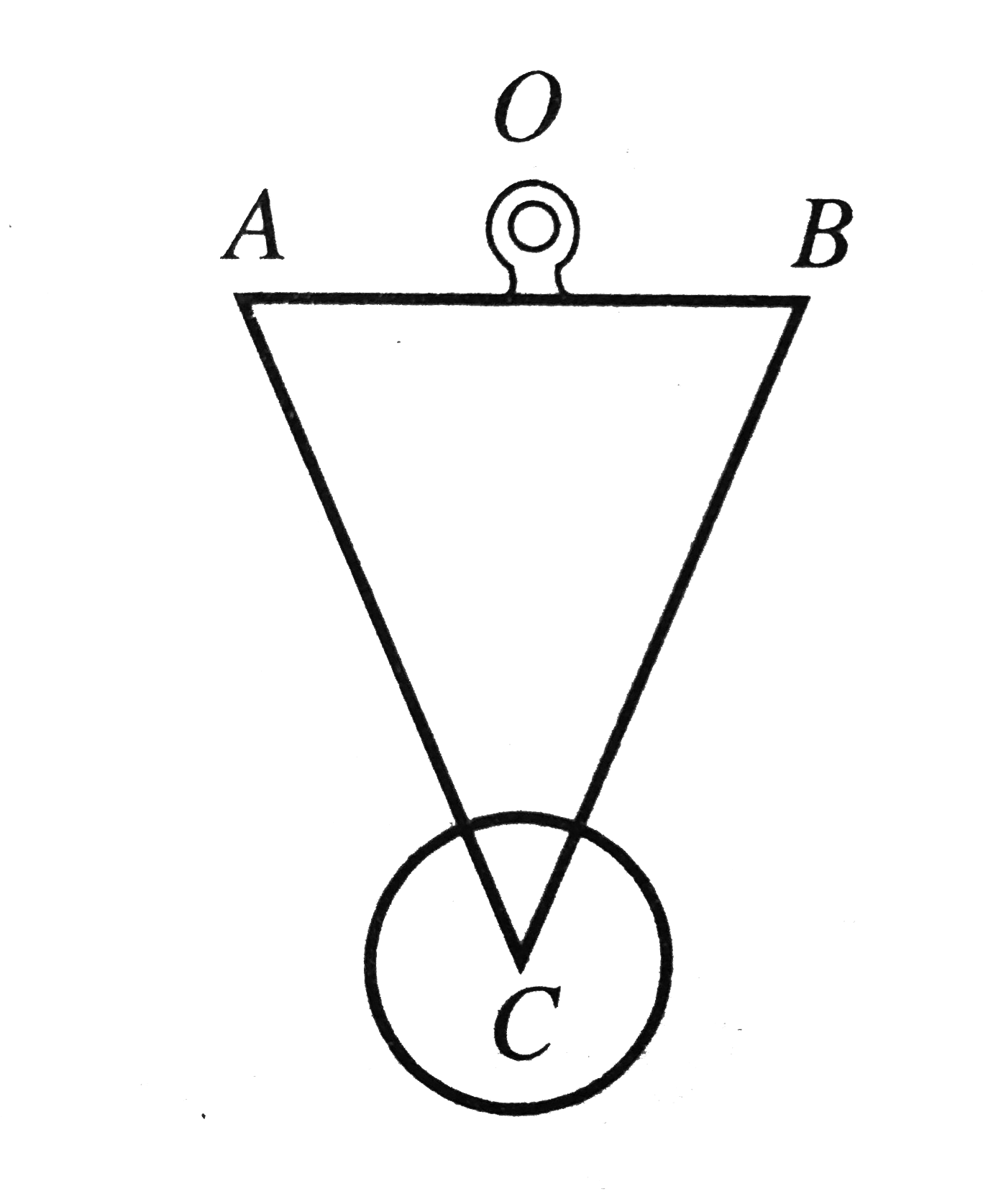
A compensated pendulum shown if Fig. is in the from of an isosceles Delta of base length `l_1=5`cm and coefficent of linar expansion `alpha_1=18xx10^-6` and side length `l_2` and coefficient of linear expansion `alpha_2=12xx10^-6`. find `l_2` so the the distance of centre of mass of the bob from suspension centre O may remain the same at all the temperature.
View SolutionTwo same length rods of brass and steel of equal cross-sectional area are joined end to end as shown in figure and supported between two rigid vertical walls. Initially the rods are unstrained. If the temperature of system is raised by `Deltat`. Find the displacement of the junction of two rods. Given that the coefficient of linear expansion and young's modulus of brass and steel are `apha_(b).alpha_(s)(alpha_(b)gtalpha_(s)),Y_(b)` and `Y_(s)` respectively.
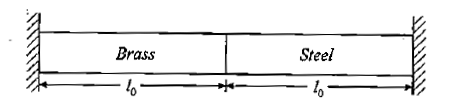
View SolutionA 1-L flask contains some mercury. It is found that at different temperature, the volume of air inside the flask remains the same. What is the volume of mercury in the flask, given that the coefficient of linear expansion of glass`=9xx10^(-6)//^(@)C` and the coefficient of volume expansion of `Hg=1.8xx10^(-4)//^(@)C` ?
View SolutionA sphere of radius 3.5 cm and mass 250 gm floats in a liquid at `20^(@)C`. As the temperature is raised, the sphere just being to sink at a temperature of `35^(@)C`. If the density of liquid at `0^(@)C` is `1.527gm//cm^(3)` find the coefficient of cubical expansion of the liquid. Neglect expansion of the sphere.
View SolutionA piece of metal weighs 46 g in air and 30 g in lipuid of density `1.24 xx 10^3 kg m^(-3)` kept at `27^0C`. When the temperature of the liquid is raised to `42^0C` the metal piece weights 30.5 g . The density of the liqued at `42^0 C` is `1.20 xx 10^3 kg m^(-3)`. Calculate the coefficient of linear expandsion of the metal.
View SolutionA sinker of weight `w_0` has an apparent weight `w_1` when weighed in a liquid at a temperature `t_1 and w_2` when weight in the same liquid at temperature `t_2`. The coefficient of cubical expansion of the material of sinker is `beta`. What is the coefficient of volume expansion of the liquid.
View SolutionA barometer reads 75 cm on a steel scale. The room temperature is `30^(@)C`. The scale is correctly graduated for `0^(@)C`. Find the correct atmosphere pressure. Given that coefficient of linear expansion of steel is `1.1xx10^(-5).^(@)C^(-1)` and that of cubical expansion of mercury is `1.8xx10^(-4).^(@)C^(-1)`. Neglect expansion of glass tube.
View SolutionA aluminium can of cylindrical shape contains `500cm^3` of water. The area of the inner cross section of the can is `125cm^2`. All measurements refer ti `10^@C`. Find the rise in the water level if the temperature increases to`80^@C`. The coefficient of linear expansion of aluminium `=23 xx 10^(-6 @ )C(-1)` respectively.
View SolutionA steel ball initially at a pressure of `10^5Pa` is heated from `20^@`C to `120^@`C keeping its volume constant. Find the final pressure inside the ball. Given that coefficient of linear expansion of steel is `1.1xx10^(-5)//^@C` and Bulk modulus of steel is `1.6xx10^(11)Nt//m^(2)`.
View SolutionA lead ball at `25^@`C is dropped from a height of 2 km. It is heated due to air resistance and it is assumed that all of its kinetic energy is used in increasing the temperature of ball. Find the final temperature of the ball. s (ball) = 126 J/kg-K
View SolutionThe temperatures of equal masses of three different liquids A, B and C are `15^@C`, `20^@C` and `30^@C`, respectively. When A and B are mixed their equilibrium temperature is `18^@C`. When B and C are mixed, it is `22^@C` .What will be the equilibrium temperature when liquids A and C are mixed
View SolutionA metal block of density `5000kg//m^(3)` and mass `2kg` in suspended by a spring of force constant `200 N//m`. The spring block system is submerged in water vessel. Total mass of water in vessel is `300 gm` and in equilibrium the block is at a height `40` cm above the bottom of vessel. The specific heat of material of block is `250J//kg//k` and that of water is `4200J//kg//k`. Neglect the heat capacities of vessel and the spring. If the support is broken the rise in temperature of water, when block reaches botton of vessel is
View SolutionA copper cube of mass `200g` slides down an a rough inclined plane of inclination `37^(@)` at a constant speed. Assume that any loss in mechanical energy goes into the copper block as thermal energy .Find the increase in the temperature of the block as it slides down through `60cm`. Specific heat capacity of copper `= 420J kg^(-1) K^(-1)`
View SolutionAn aluminium vessel of mass `0.5kg` contains `0.2kg` of water at `20^(@)C`. A block of iron of mass `0.2kg` at `100^(@)C` is gently put into the water .Find the equilibrium temperature of the mixture.
Specific heat capacities of aluminium , iron and water are `910 J kg^(-1)K^(-1) ,470J kg^(-1)K^(-1) and 420J kg^(-1)K^(-1)` respectively.
View SolutionFind the result of mixing 0.5 kg ice at `0^@C` with 2 kg water at `30^@C`. Given that latent heat of ice is `L=3.36xx10^5 J//kg` and specific heat of water is `4200 J//kg//K`.
View SolutionWhen 2 kg blocmk of copper at `100^(@)C` is put in an ice container with 0.75 kf og ice at `0^(@)C`, find the equilibrium temperature and final composition of the mixture. Given that specific heat of copper is 378 J/kg K and that of water is 4200J/kg K and the latent heat of fusion of ic eis `3.36xx10^(5)` J/kg
View SolutionHow should `1 kg` of water at `50^(@)C` be divided in two parts such that if one part is turned into ice at `0^(@)C`. It would release sufficient amount of heat to vapourize the other part. Given that latent heat of fusion of ice is `3.36xx10^(5) J//Kg`. Latent heat of vapurization of water is `22.5xx10^(5) J//kg` and specific heat of water is `4200 J//kg K`.
View SolutionIn a pitcher when water is filled some water comes to outer surface slowly through its porous walls and gets evaprated. Most of the latent heat needed for evaporation is taken from water inside and hence this water is cooled down. If 10 kg water is taken in the pitcher and 12 gm water comes out and evaporated per minute. Neglect heat transfer by convection and radiation to surrounding, find the time in which the temperature of water is pitcher decreases by `5^(@)C`.
View Solution
ILLUSTRATIVE EXAMPLE questions and complete solutions for chapter HEAT AND THERMAL EXPANSION of GK PUBLICATIONS PHYSICS (HINGLISH) of Class 12