Complete Solutions to UNSOLVED NUMRICAL PROBLEMS FOR PREPARATION OF NSEP, INPhO & IPhO of chapter HEAT AND THERMAL EXPANSION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | HEAT AND THERMAL EXPANSION |
| PHYSICS GALAXY | UNSOLVED NUMRICAL PROBLEMS FOR PREPARATION OF NSEP, INPhO & IPhO |
| Number Of Questions | 82 |
| Academic Year | 2023-24 |
In a vertical `U`-tube containing a luquid, the two arms are maintained at different temperatures, `t_(1)` and `t_(2)` . The liquid coplumns in the two arms have heights `l_(1)` and `l_(2)` respectively. The coefficient of volume expansion of the liquid is equal to

View SolutionHow many kilograms of copper will experience the same temperature rises as 10 kg of water when the same amount of heat is absorbed? `(S_(cu)=0.09"cal"//g.^(@)C`)
View SolutionIf coal gives off 7000 kcal/ kg when it is burnt, how much coal will be needed to heat a house that requires `4.2xx10^(7)` kcal for the whole winter? Assume that an additional 30 percent of the heat is lost up the chimney.
View SolutionHow much water would have to evaporate from the skin per minute to make away all the heat generated by the basal metabolism (60 kcal/h) of a 65 kg person?
View SolutionDuring exercise, a person may give offf 180 kcal of heat in 30 min by evaporation of water from the skin. How much water has been lost? Given that latent heat of vaporization of water is 540 cal/gm.
View SolutionA 55.0 kg ice skater moving at 8.5 m/s glides to a stop. Assuming the ice is at `0^(@)C` and that 50 percent of the heat generated by friction is absorbed by the rice, how much ice melts?
View SolutionThe design of some physical instrument requires that there be a constant difference in length of 10 cm between an iron rod and a copper cylinder laid side by side at all temperature find their lengths
`(alpha_(Fe)=11 xx 10^(6).^(@)C^(-1),alpha_(Cu)=17 xx 10^(-6) .^(@)C^(-1))`
View SolutionA steel rod 25 cm long has a cross -sectiional area of `0.8cm^(2)`. What force wouyld be required to stretch this rod by the same amount as the expansion produced by heating it by `10^(@)C`? Given that for steel coefficient of linear expansion and Young's modulus are given as `alpha=1.1xx10^(-5).^(@)C^(-1)` and `Y=2xx10^(11)Nm^(-2)`
View SolutionHow should 1 kg of water at `5^@C` be divided into two parts so that if one part turned into ice at `0^@C`, it would release enough heat to vapourize the other part? Latent heat of steam`=540 cal//g` and latent heat of ice `=80 cal//g`.
View SolutionA steel wire of cross sectional area `5xx10^(-7)m^(2)` is tied between two rigid clamps. It is given that at `30^(@)C` wire is just taut. If the temperature of wire is decreased to `10^(@)C`, find the tension in the wire. Given that the coefficient of linear expansion of stees is `1.1xx10^(-5).^(@)C^(-1)` and its Young's modulus is `2xx10^(11)N//m^(2)`
View SolutionA bar measured with a vernier caliper is found to be 180 mm long. The temperature during the measurement is `10^@C`. The measurement error will be if the scale of the vernier caliper has been graduated at a temeprature of `20^@C`. (`alpha=1.1xx10^(-5).^(@)C^(-1)`. Assume that the length of the bar does not change.)
View SolutionThe brass scale of a mercury barometer has been graduated at `0^(@)C`. At `18^(@)C` the barometer shows a pressure of 760 mm. Reduce the reading of the barometer to `0^(@)C`. The coefficient of linear expansion of brass `=1.9xx10^(-5)=1` and the coefficient of volume expansion of mercury `gamma=1.8xx10^(-4).^(@)C^(-1)`
View SolutionA piece of metal weighs 46 g in air and 30 g in lipuid of density `1.24 xx 10^3 kg m^(-3)` kept at `27^0C`. When the temperature of the liquid is raised to `42^0C` the metal piece weights 30.5 g . The density of the liqued at `42^0 C` is `1.20 xx 10^3 kg m^(-3)`. Calculate the coefficient of linear expandsion of the metal.
View SolutionCalculate the percentage increase in the moment of inertia of a ring of iron. Given that `alpha_("iron")=11xx10^(-6).^(@)C^(-1)` and rise in temperature is `20^(@)C`
View SolutionA gas heated geyser consumes `V_(00=1.8cm^(3)` of methane `(CH_(4))` in an hour. Find the temperature of the water heated by the geyser if the water flows out at the rate of v=50 cm/s. The diameter of the stream D=1cm, the initial temeprature of the water and the gas is `t_(1)=11.^(@)C` and teh calorific value of methane is `q_(0)=13` kcal/g. The gas in the tube is under a pressure of 1.2 atm. the efficiency of the heater is `eta=60%`
View SolutionA mixture of 250 g of water and 200 g of ice at `0^@C` is kept in a calorimeter which has a water equivalent of 50 g. If 200 g of steam at `100^@C` is passed through this mixture, calculate the final temperature and the weight of the contents of the calorimeter.
View SolutionAn earthware vessel loses 1 g of water per second due ot evaporation. The water equivalent of the vessel is 0.5 kg and the vessel contains 9.5 kg of water. Find the time required for the water in the vessel to cool to `28^(@)C` from `30^(@)C`. Neglect radiation losses. Latent heat of vaporisation of water in this range of temperature is 540 cal/g.
View SolutionA steel rule is calibrated at `22^(@)C` against a standard so that the distance between numbered divisiions is 10.00 mm. a. What is the distance between these divisions when the rule is at `-5^(@)C`? (b) If a nominal length of 1 is measured with the rule at this lower temperature, what percent error is made? c. What absolute error is made for a 100 m length?
[`alpha_(st)=1.1xx10^(-5).^(@)C^(-1)`]
View SolutionAn iron cube floats in a bowl of liquid mercury at `0^(@)C` a. if the temperature is raised to `30^(@)C` will the cube float higher or lower in the mercuyr? B. By wat percent will the fraction of volume submerged change?
View SolutionA precise steel tape measure has been calibrated at `20^(@)C`. At `40^(@)C` a. will it read high or low, and b. what will be the percentage error?
View SolutionAn 18-g ice cube (at `0^(@)C`) is dropped into a glass containing 200 g of water at `25^(@)C` . If there is negligible heat exchange with the glass, what is the temperature after the ice melts?
View SolutionA bimetalis strip conists of two metakl strips with diffesrent coefficients of linear expansion `alpha_(1)` and `alpha_(2)` each of small thickness d and length `L_(0)` at `T_(0)`. They are bonded together and, with a change in temperature `DeltAT`, will curve in a circular arc, as shown in figure. Show that the radius of curvature R is given approximately be
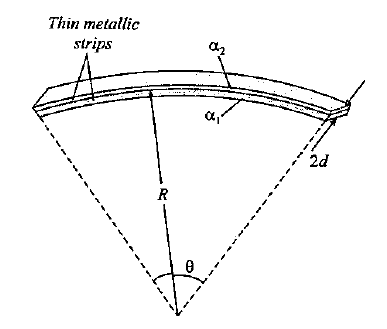
`R=d/((alpha_(2)-alpha_(1))DeltaT)`
View SolutionA thin smooth tube of length 2 m containing a small pallet of mercury in it is rapidly inverted 50 times. If capillary effect is neglected find the approximate increase in temperature of the mercury. Given that the specific heat of mercury is 30 cal/kg K.
View SolutionFrom what height must a block of ice fall to just melt by the impact assuming that half of the heat generated is absorbed by ice? (`J=4.2` joules per calories and `L=80` kilocalories per kg)
View SolutionA hole is drilled into a block of lead of mass `10kg` by a driller. The driller is driven by an electric motor of 30 r.p.m. and the couple exerted by the motor on the driller is `10Nm`. Calculate the rise in temperature of the lead in 10 minutes. `J=4.2` joules `cal^(-1)`. Relative specific heat capacity of lead 0.03 and sp. heat capacity of water `1000 cal kg^(-1)K^(-1)`.
View SolutionA mercury thermometer is to be made with glass tubing of internal bore 0.5 mm diameter and the distance between the fixed point is to be 20 cm. Estimate the volume of the bulb below the lower fixed point, given that the coefficient of cubical expansion of mercury is `0.00018//K`. and the coefficient of linear expansion of glass is `0.000009//K`.
View SolutionA lump of ice of 0.1 kg at `-10^(@)C` is put in 0.15 kg of water at `20^(@)C`. How much water and ice will be found in the mixture whenit has reached thermal equilibrium? Specific heat of ice `=0.5kcal kg^(-1).^(@)C^(-1)` and its latent heat of melting `=80` kcal `kg^(-1)`
View SolutionA metallic bob weights `50 g` in air. If it is immersed in a liquid at a temperature of `25^@ C`, it weights `45 g` . When the temperature of the liquid is raised to `100^@ C`, it weights `45.1 g`. Calculate the coefficient of cubical expansion of the liquid. Given that coefficient of cubical expansion of the metal is `12 xx 10^(-6) .^@ C^-1`.
View SolutionA copper calorimeter of mass 190 g contains 300 g of water at `0^(@)C` and 50 g of ice at `0^(@)C`.Find the amount of steam at `100^(@)C` required to raise the temperature of this mixture by `10^(@)C`. Given that the specific heat of copperis `420J//kg^(@)C`, latent heat of vaporization of water is `2.25xx10^(5)xxJ//kg` and latent heat of fusion of ice is `3.36xx10^(5)J//kg`.
View SolutionIn an industrial process 10 kg of water per hour is to be heated from `20^@C` to `80^@C`. To do this steam at `150^@C` is passed from a boiler into a copper coil immersed in water. The steam condenses in the coil and is returned to the boiler as water at `90^@C`. How many kilograms of steam is required per hour (specific heat of steam`=1 cal//g^@C`, Latent heat of vapourization`=540 cal//g`)?
View SolutionIn the past it was practice to measure temperature using so called weight thermometer which consists of glass sphere having a narrow flow out tube. Such a certain weight thermometer is completely filled with 14.578 g of liquid at `15^(@)C`. It is found that 1.232 g of liquid over flows when the temperature is raised to `100^(@)C`. How much more liquid overflow when the temperature is further raised to `200^(@)C`?
View SolutionA barometer having a brass scale reads 77.24 cm at a temperature of `20^(@)C`. The scale is graduated to be accurate at `0^(@)C`. What would be the readint at `0^(@)C` ? Coefficient of cubical expansion of mercury `=18xx10^(-5).^(@)C^(-1)` and linear expansion of brass `-19xx10^(-6).^(@)C^(-1)`
View SolutionA horizontal thin copper ring has a diameter exactly 1.00000 inch at temperature `0^(@)C` and is ficed to a non conducting stand. An aluminium sphere of diameter exactly 1.00200 inch at `100^(@)C` is placed on the top of the ring. When the two attain temperature equilibrium, the sphere just passes through the ring. Assuming that the whole heat energy remains within the ring sphere system find
(`alpha_(Cu)=1.67xx10^(-5).^(@)C^(-1), alpha_(Al)=2.4xx10^(-4).^(@)C^(-1)`)
(i) the final equilibrium temperature
(ii) the ratio of the mass of the ring to that of the sphere.
View SolutionAniline is a liquid which does not mix with water. When a small quantity of it is poured into a beaker of water at `20^(@)C`, it sinks to the bottom. The densities of aniline and water at `20^(@)C` and `1021 kgm^(-3)` and `998 kgm^(-3)` respectively. Find the minimum temperature to which the mixture is to be heated so that aniline will form a globule and just start floating.
`gamma_("aniline")=85xx10^(-5).^(@)C^(-1), gamma_("water")=45xx10^(-5).^(@)C^(-1)`.
View SolutionDuring light activity a `70 kg` person may generate `200` kcal/hr. Assuming that `20%` of this goes into useful work and the other `80%` is converted to heat, calculate the temperature rise of the body after `1.00hr` if none of this heat is transferred to the environment. Assume specific heat of the human body is `450 "cal"//kg^(@)C`
View SolutionA makki ki roti has 100 kcal of thermal energy. What a man of 60 kg eats five such roti, how many meters can he climb by using this energy. Given that the working efficiency of man is 30% of the total energy gain by eating.
View SolutionA copper calorimeter of negligible thermal capacity is filled with a liquid. The mass of the liquid is 250 gm. A heating element found that the temperature of the calorimeter and its contents rise form `25^(@)C` to `30^(@)C` in 5 minutes when a current of 2.05 A is passed through it at al potential difference of 5 volts. The liquid is thrown off and the heater is switched on again. it is now found that the temperature of the calorimeter alone remains constant at `32^(@)C` when the current through the heater is 0.7 A at the potential difference 6 volts. Calculate the specific heat capacity of the liquid. The temperature of the surrounding is `25^(@)C`
View SolutionA long horizontal glass capillary tube open at both ends contains a mercury thread 1 m long at `0^@C`. Find the length of the mercury thread, as read on this scale, at `100^@C`.
`(gamma_("mercury")=18.2xx10^-5K^-1alpha_("glass")=9xx10^-6K^-1)`
View SolutionIce with mass `m_(1)=600g` and at temperature `t_(1)=-10^(@)C` is placed into a copper vessel heated to `t_(2)=350^(@)C`. As a result, the vessel now contains `m_(2)=550g` of ice mixed with water. Find the mass of the vessel. The specific heat of copper `=0.1"cal"//C^(@)g` and sp. heat of ice `=0.5"cal"//gC^(@)`. Latent heat of ice `=80"cal"//g`.
View SolutionA metal rod of length 5 m placed on a smooth tabel. Given that Young's modulus of the material of the rod is `1.6xx10^(11)N//m^(2)` and the its coefficient of linear expansion is `1.2xx10^(-5).^(@)C^(-1)`. If temperature of rod is changed from `20^(@)C` to `80^(@)C` find the elastic stress developed in the rod.
View SolutionAn ice block of volume `3.2xx10^(-5)m^(3)` and at temperature `0^(@)C` is put in 200 gm water at `10^(@)C`. Find the temperature and composition of mixture when thermal equilibrium is attained. Given that density of ice is `900 kg//m^(3)`, specific heat of water is `4200 J//kg^(@)` C and latent heat of fusion of ice `.4xx10^(-5)J//kg`
View SolutionA body made up of an alloy (40% copper +60% nickel) of mass 0.1 kg is placed in a container of water equivalent 10 gm which contains 90 g of water at `10^(@)C`. If the equilibrium temperature is `20^(@)C`, find the initial temperature of the body. Given that specific heat of water is `4200 J//kg^(@)C` and that of copper is `420J//kg^(@)C` and that of nickel is `460 J//kg^(@)C`
View SolutionA block of `10 kg` mass is thrown on a rough surface having friction coefficient `0.3` with an initial speed of `5` m/s. Find the amount by which the internal energy of the blocked and the surface will increase. If this block is seen from a frame moving at a speed of `5` m/s in the direction of its velocity it is observed that the block is gently put on the rough surface moving in opposite direction at speed `5` m/s. Find the gain kinetic energy of the block as seen from this frame.
View SolutionA vessel is completely filled with `500g` of water and `1000g` of mercury. When 21,200 calories of heat are given to it `3.52g` of water overflows. Calculate the volume expansion of mercury. Expansion of the vessel may be neglected. Given that coefficient of volume expansion of water `=1.5xx10^(-4)//C^(@)`, density of mercury `=13.6g//cm^(3)`, density of water `e=1g//cm^(3)`, and specific heat of mercury `=0.03"cal"//gC^(@)`
View SolutionWhen a certain quantity of liquid bismuth at its melting point of `271^(@)C` is transferred to a calorimeter contaiing oil, the temperature of oil from `13.4^(@)C` to `28.5^(@)C`. When the experiment under identical conditions except that bismuth is in solid form, the temperature of oil rises to `19^(@)C` if the specific heat of bismuth is `0.134Jg^(-1).^(@)C^(-1)`, fine the metal heat of fusion of bismuth
View SolutionAn iron plug is to be placed in a ring made of brass. At room temperature `28^(@)C` the diameter of the plug is 9.114 cm and that of the inside of the ring is 9.097 cm. To what common temperatue these both be brought in order to fit? Give that coefficient of linear expansion of iron is `1.1xx10^(-5).^(@)C^(-1)` and that of brass sis `1.9xx10^(-5).^(@)C^(-1)`
View SolutionThe 0.50 kg head of a hammer has speed of 5.0 m//s just before its strikes a nail and is brought to rest. Estimate the temperature rise a 15 g nail generated by ten such hammer blows done in quick succession. Assume the nail absorbs all the heat.
View SolutionTwo metal spheres (10 kg and 30 kg) moving towards each other at speeds 10 m/s and 20 m/s respectivley.They collide inelasticity. What is the rise in temperature of the combined body after collision if al the energy lost appears in the form of heat. Given that specific heat of the metal of spheres is `0.03 "cal"//g^(@)C`
View SolutionA 25 g bullet travelling at 400 m//s passes through a thin iron wall and emerges at a speed of 250 m/s. If the bullet absorbs 50 percent of the heat generated, a. what will be the temperature rise of the bullet? B. If the ambient temperature is `20^(@)C` will the bullet melt, and if so how much? Given that specific heat of head is `0.03 "cal"//gm^(@)C` and latent heat of fusion of lead is 6000 cal/kg. It is also given that melting pont of lead is `320^(@)C`.
View SolutionAbout 5 g water at `30^(@)C` and `5 g` is at `-20^(@)C` are mixed in a container of negligible heat capacity. Find the final temperature and composition of the mixture. Given that specific heat of water is `4200J//kg^(@)C` and that of ice of `2100//kg^(@)C` and latent heat of ice is `3.36xx10^(5)`J/Kg
View SolutionA brass pipe that is 10 cm indiameter and has a wall thickness of 0.26 cm carries steam at `100^(@)C` through a vat of circulating water at `20^(@)C`. How much heat is lost per meter of pipe in 1s?
View SolutionThe tube of a mercury thermometer has an inside diameter of `0.120`mm.The bulb has a voluem of `0.250cm^(3)`. How far will the thread of mercury move when the temperature changes from `10.0^(@)C` to `20.0^(@)C`? Take inot account expansion of the glass (Pyrex). b. Determined a formula for the length of the mercury column in terms of relavant variables.
View Solution200 g of water and equal volume of another liquid of masss 250 g areplaced in turn in the same calorimeter of mass 100 g and specific heat capacity 420 J/kg K. The liquids which are constantly stirred are found to cool from `60^(@)C` to `20^(@0C` in 3 minutes and 2 minutes 20 seconds, respectively. Find the specific heat capacity of the liqudi. The temperature of the surrounding is `20^(@)C`.
View SolutionFigure shows a wheel pivoted at its centre in a water tank containing 1 kg water. A light string is wound on the shaft of the wheel and its other end is connected to a hainging block of mass 12 kg as shown. It is observed that the block falls slowly by a distance 0.7 m. Find the rise in temperature of the water. Also find the amount of theat supplied to the water. Give that the specific heat fo water is `4200J//kg^(@)C` and that of wheel is negligible.

View Solution0.6 kg of ice at `-10^(@)C` is place in a copper calorimeter at `350^(@)C`. After some time when thermal equilibrium is attained, calorimeter contains 550 g of ice with some water. Find the water equivalent of the calorimeter. Given that the specific heat of copper is 420 J/kgK, and that of ice `2100J//kg^(@)C` and latent heat of ice is `3.32xx10^(-5)J//kg` check the answer
View SolutionTwo pendulum clocks, one having an iron pendulum and the other having a brass pendulu, are keeping correct time at `5^(@)C`. How much per day will they differ at `25^(@)C`?
`alpha_("iron")=12xx10^(-5).^(@)C^(-1), alpha_("brass")=18.7xx10^(-6).^(@)C^(-1)`
View SolutionAS 12.4 kg solid iron cylindrical wheel of radius 0.45 m is rotating about its axle in frictionless bearings with angular velocity `omega=32.8` rad/s. If its temperature is now raised from `20^(@)C` to `80^(@)C` what is the fractional change in `omega`? Given that coefficient of linear exapansion of iron is `1.1xx10^(-5).^(@)C^(-1)`
View SolutionWhen a man does exercise on a treadmill machine, work doen by him is supplied in the form of heat of an ice bath. Find how much he has to do to convert a piece of 5 gm of ice at `-3^(@)C` to steam at `100^(@)C`.Given that the specific heat of ice is 0.5 cal/`gm^(@)C`, latent heat of fusion of ice is 80 cal/gm and laten heat of vaporization of water is 540 cal/gm.
View SolutionA steel ball, of mass 10 g and specific heat `100 "cal"//kg(@)C`, is pushed out after being heated inside a furnace. It is quickly caught inside a thick copper vessel of mass 200 g and relative specific heat 0.09 at `50^(@)C` and the vessel is dropped into a calorimeter of water equivalent 20 g containing 180 g of water at`20^(@)C`. The thermometer in the calorimeter shows maximum temperature of `26^(@0C`. Calculate the temperature of the furnace and find the calculation whether there was any local boiling in the calorimeter.
View SolutionAt a temperature of `20^(@)C`, the volume of a certain glass flask, up to a reference mark on the cylindrical stem of the flask is exactly is `100 cm^(3)`. The flask is filled to this point with a liquid of coefficient of cubical expansion `120xx10^(-5).^(@)C^(-1)`., when both the flask and the liquid are at `20^(@)C`. The corss section ofthe stem is `1mm^(@)` and the coeffiocient of linear expansion of glass is `8xx10^(-5).^(@)C^(-1)`. Fidn the rise of fall of the liquid level in the stem, when the temperature is raised to `40^(@)C`.
View SolutionFind the final temperature and composition of the mixtue of 1 kg of ice at `0^(@)C` and 1.5 kg of water at `45^(@)C`. Given that specific heat of water is 4200 J/kg and latent heat of fusion of ice is `3.36xx10^(5)J//kg`
View SolutionA solid substance of mass 10 g at `-10^(@)C` was heated to `-2^(@)C` (still in the solid state). The heat required was 64 calories. Another 880 calories was required to raise the temperature of the substance (now in the liquid state) to `1^(@)C`, while 900 calories was required to raise the temperature from `-2^(@)C` to `3^(@)C`. Calculate the specific heat capacities of the substance in the solid and liquid state in calories per kilogram per kelvin.
View SolutionThe volume of a mixture of ice and water is found to decrease by `0.125xx10^(-6)m^(3)` without change in temperature when `10xx10^(-3)kg` of a metal at `100^(@)C` is immersed into it. The relative density of ice is `0.917`. Find the specific heat capacity of the metal.
View SolutionWater in a fall falls through h=1.0 km considering this as a thermodynamical process, calculate the difference in temperature of water at the top and bottom of the fall. Specific heat of water `=1000"cal"//kg^(@)C` and J=4.2J/cal.
View SolutionA calorimeter of specific heat 0.42 J/gm`.^(@)C` and weighing 40 g contains 50 g of water mixed with 50 g of ice. Dry steam at `100^(@)C` is passed into the mixture until the temperature rises to `20^(@)C`. Find the mass of steam condensed.
View SolutionHow much steam at `100^(@)C` is needed to change 40 g of ice at `-10^(@)C` to water at `20^(@)C` if the ice in a 50 g copper can? Assume that the can maintains the same temperature as the ice and water. Given that specific heat of copper is `S_(Cu)=0.09 "cal"//gm^(@)` and specific heat of ice is `S_("ice")=0.5` cal /gm`.^(@)C` .
View SolutionA vertical steel beam at the base of buiolding is 6.0 m tall, thas a mass of 300 kg, and supports a load of `3.0xx10^(5)N`. If the beam's temperature decreases by`4.0^(@)C`, calculate the change in its internal energy using the facts that for steel `c_(p)` is `0.11 "kcal"//kg^(@)` and the coefficient of the linear expansion is `11xx10^(-6).^(@)C^(-1)`
View SolutionA heavy brass bar has projections at its ends as shown in the figure. Two find steel wires, fastened between the projections, are just taut (zero tension) when the whole systeam is at `0^(0)C`. What is the tensile stress in the steel wires when the temperature of the systeam is raised to `300^(0)C`?
Given that
`alpha_("brass") = 20 xx 10^(-6 ^(@))C^(-1)`
`alpha_("steel") = 12 xx 10^(-6@)C^(-1) Y_("steel") = 2 xx 10^(11) Nm^(-2)`
_E01_077_Q01.png)
View SolutionFind the final temeprature and composition of the mixture of 1 kg of ice at `-10^(@)C` and 4.4 kg of water at `30^(@)C`. Given that specific heat of water is `4200J//kg^(@)C` and that of ice is `2100J//kg^(@)C` and latent heat of fusion of ice is `3.36xx10^(5)`J/kg
View SolutionSuppose that 40 g of solid mercury at its freezing point `(-39^(@)C)` is dropped into a mixture of water and ice of `0^(@)C`. After equilibrium is achieved, the mercury -ice -water mixture is still at `0^(@)C`. How much additiional ice is produced by the addition of the mercury?
View SolutionA calorimeter contains ice. Determine the heat capacitiy of the calorimeter if `2.1kJ` of heat is required to heat it togheter with its contents from `270^(@)K` to `272^(@)K`, and `69.72kJ` of heat of required to raise its temperature of `272K` to `274^(@)K`.
(`L` of ice `=336xx10^(3)Jkg^(-1)`, specific heat capacity of ice `=2100kg^(-1)K^(-1)`)
View SolutionA steel drill making 180 rpm is used to drill a hole in a block of steel. The mass of the steel block and the drill is 180 gm. If the entire mechanical work is used up in producing heat and the rate of raise in temperature of the block and the drill is 0.5 °C/s. Find
(a) the rate of working of the drill in watts, and
(b) the torque required to drive the drill. Specific heat of steel `= 0.1 and J = 4.2 J//cal`. Use : `P = tau omega`
View Solution
A substance is in the solid form at `0^@`C. The amount of heat added to this substance and its temperature are plotted in the following graph. If the relative specific heat capacity of the solid substance is 0.5, find from the graph (i) the mass of the substance, (ii) the specific latent heat of the melting process and (ii) the specific heat of the substance in the liquid state.
Specific heat capacity of water `=1000 cal//kg//K`
View SolutionSteam at `100^@C` is passed into a calorimeter of water equivalent 10 g containing 74 cc of water and 10 g of ice at `0^@C`. If the temperature of the calorimeter and its contents rises to `5^@C`, calculate the amount of steam passed. Latent heat of steam`=540 kcal//kg`, latent heat of fusion`=80 kcal//kg`.
View SolutionAn electron beam travelling at a speed of `10^(7)` m/s strikes a metal target and absorbed by it. If the mass of the target is 0.5 g its specific heatis 100 cal /kg`.^(@)C`, find the rate at which its temperature rises. Given that the electron beam curen is 0.048 A.
View SolutionSome water at `0^@C` is placed in a large insulated enclosure (vessel). The water vapour formed is puped out continuously. What fraction of the water will ultimately freeze, if the latent heat of vapourization is seven times the latent heat of fusion?
View SolutionThe apparatus shown in the figure consists of four glass columns connected by horizontal section. The height of two central column B and C are 49 cm each. The two outer columns A and D are open to the temperature. A and C are maintained at a temperature of `95^@C` while the columns B and D are maintained at `5^@C`. The height of the liquid in A and D measured from the base the are 52.8 cm and 51cm respectively. Determine the coefficient of thermal expansion of the liquid
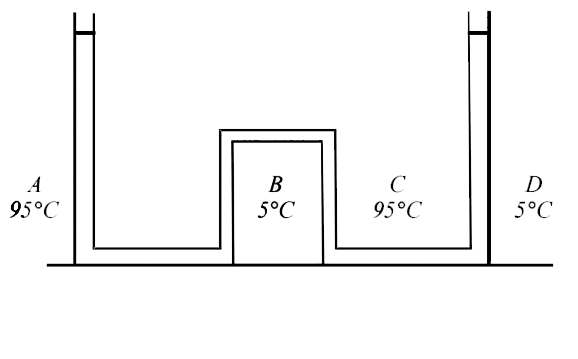
View SolutionA non conducting vessel thermally insulated from its surroundings, contains 100 g of water `0^(@)C`. The vessel is connected to a vacuum pump to pump to water vapour. As a result of this, some water is frozen. If the removal of water vapour is continued, what is the maximum amount of water that can be frozen in this manner? Laten heat of vaporisation of water `=22.5xx10^(5)Jkg^(-1)` and latent heat of fusion of ice `=3.36xx10^(5)Jkg^(-1)`
View SolutionA mercury in glass thermometer has a stem of internal diameter 0.06 cm and contains 43 g of mercury. The mercury thread expands by 10 cm when the temperature changes from `0^@C` to `50^@C`. Find the coefficient of cubical expansion of mercury. Relative density of mercury `=13.6` and `alpha_("glass")=9xx10^(-6)//K`.
View SolutionA loaded and completely sealed glass bulb weighs 156.25 gm inair at `15^(@)C`, 57.5 gm when completely immersed in a liquid at `15^(@)C` and `58.57` gm when completely immersed at `52^(@)C`. Calculate the mean coefficient of real expansion of the liquid between `15^(@)C` and `52^(@)C`. `alpha_("glass")9x10^(6).^(@)C^(-1)`
View SolutionA certain amount of ice is supplied heat at a constant rate for 7 minutes. For the first one minute the temperature rises uniformly with time. Then, it remains constant for the next 4 minute and again the temperature rises at uniform rate for the last two minutes. Calculate the final temperature at the end of seven minutes.
(Given, L of ice `= 336 xx (10^3) J//kg` and specific heat of water `= 4200 J//kg.K`).
View SolutionTwo cylinders of equal masses, one made of aluminium and the other of copper, with their lateral surfaces thermally insulated, are heated to `50^(@)C` and placed on two large blocks of ice at `0^(@)C`. If both the cylinders haver the same height, find the ratio of their depths of penetration in the ice. Assume that no heat is lost to the surroundings. Given that
`S_(Al)=0.22 "cal" gm^(-1).^(@)C^(-1), rho_(Al)=2.7gm cm^(-3)`
`S_(CU)=0.1 "cal"gm^(-1).^(@)C^(-1),rho_(Cu)=8.9gm cm^(-3)`
View Solution
UNSOLVED NUMRICAL PROBLEMS FOR PREPARATION OF NSEP, INPhO & IPhO questions and complete solutions for chapter HEAT AND THERMAL EXPANSION of GK PUBLICATIONS PHYSICS (HINGLISH) of Class 12