Complete Solutions to Practice Exercise 5.2 of chapter ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENT of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENT |
| PHYSICS GALAXY | Practice Exercise 5.2 |
| Number Of Questions | 14 |
| Academic Year | 2023-24 |
A magnetic flux through a stationary loop with a resistance `R` varies during the time interval `tau` as `phi=at(tau-t)`. Find the amount of the generated in the loop during that time
02:05View SolutionA long solenoid having 1000 turns per cm carries an alternating current of peak value 1 A. A search coil having a cross-sectional area of `1xx10^(-4) m^(2)` and 20 turns is kept in the solenoid so that its plane is perpendicular to the axis of the solenoid. The search coil registers a peak voltage of `2.5xx10^(-2)` V. Find the frequency of the current in the solenoid.
02:57View SolutionTwo infinite long straight parallel wires A and B are separted by 0.1m distance and carry equal currents in opposite directions. A square loop of wire C of side 0.1m lies in the plane of A and B. The loop of wire C is kept parallel to both A and B at a distance of 0.1m from the nearest wire. Calculate the EMF induced in the loop C while the currents in A and B are increasing at the rate of `10^(3) A//s`. Also indicate the direction of current in the loop C.
03:15View SolutionA flat circular coil of 200 turns of diameter 25 cm is laid on a horizontal table and connected to a ballistic galvanometer. The complete circuit is having resistance of `800Omega`. When the coil is quickly turned over, the spot of light swings to a maximum reading of 30 divisions. When a `0.1mu F` capacitor charged to 6 V is discharged through the same ballistic galvanometer, a maximum reading of 20 division is obtained. Calculate the vertical component of the earth's magnetic induction.
View SolutionA rectangular frame ABCD, made of a uniform metal wire, has a straight connection between E and F made of the samae wire, as shown in fig. AEFD is a square of side 1m, and EB=FC=0.5m. The entire circuit is placed in steadily increasing, uniform magnetic field directed into the plane of the paper and normal to it. The rate of change of the magnetic field is `1T//s`. The resistance per unit length of the wire is `1omega//m`. Find the magnitude and directions of the currents in the segments AE, BE and EF.
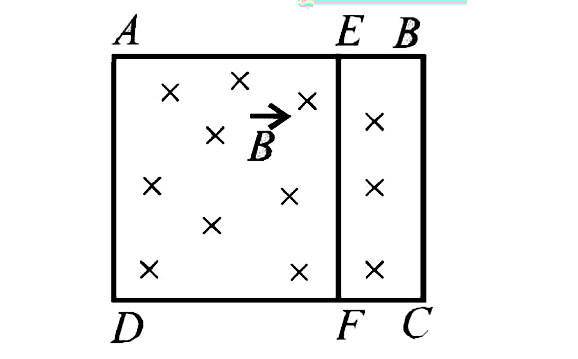 10:44View Solution
10:44View SolutionIn a long staright solenoid with cross-sectional radius `a` and number of turns per unit length `n` a current varies with a constant velocity` dotI A//s`. Find the magntidue of the eddy current field strength as a function of the distance `r` from the solenoid axis. Draw the appoximate plot of this function.
03:58View SolutionA thin non-conducting ring mass `m`, radius `a`, carrying a charge `q` can rotate freely about its own axis which is vertical. At the initial moment the ring was at rest and no magnetic field was present. At instant `t = 0`, a uniform magnetic field is switched on which is vertically downwards and increase with time according to the law `B = B_(0)t`. Neglecting magnetism induced due to totational motion of the ring. Now answer the following questions.
The power developed by the forces acting on the ring, as a function of time :04:20View SolutionIn the middle of a long solenoid there is a coaxial ring of square cross-seciton, made of conducting materaial with respectivity are equal to `h` its inside and outside radii are equal to `a` and `b` respectively. Find the current induced in the ring if the magnetic induction produced by the solenoid varies with time as `B = beta t`, where `beta t`, where `beta` is constant. THe inductance of the ring is to be neglected.
04:04View SolutionA long solenoid of diameter 0.1 m has `2 xx 10^(4)` turns per meter. At centre of the solenoid is 100 turns coil of radius 0.01 m placed with its axis coinciding with solenoid axis. The current in the solenoid is decreased at a constant rate form + 2 A to - 2 A in 0.05 s. Find the e.m.f. induced in the coil. Also, find the total charge flowing through the coil during this time, when the resistance of the coil is `10 pi^(2) ohm`.
04:08View SolutionA long solenoid of cross-sectional radius `a` has a thin insulates wiere ring tightly put on its winding, one half of the ring has the resistance `eta` times that of the other half. The magneticv induction produced by the solenoid varies with the time as `B = bt`, where `b` is a constant. Find the magnitude of the electric field strength in the ring.
09:03View SolutionA magnetic field induction is changing in magnitude at a constant rate `dB//dt` . A given mass `m` of copper is drawn into a wire of radius `alpha` and formed into a loop of radius `r` is placed perpendicular to the field. Show that induced current in the loop is given by `i=(m)/(4pipdelta)(dB)/(dt)`
`p` : resistivity, `delta` : density of copper.05:52View SolutionA long solenoid of cross-sectional area `5.0 cm^2` is wound with 25 turns of wire per centimetre. It is placed in the middle of a closely wrapped coil of 10 turns and radius 25 cm as shown.

(a) What is the emf induced in the coil when the current through the solenoid is decreasing at a rate `-0.20 A//s` ?
(b) What is the electric field induced in the coil?02:09View SolutionIn a coil of resistance R, magnetic flux due to an external magnetic field varies with time as `phi=k(C-t^(2))`. Where k and C are positive constants. Find the total heat produced in coil in time t=0 to t=C.`
02:16View SolutionFigure-5.77. shows a fixed coil of N turns and radius a carrying a current I. At a distance x from its centre another small coaxial coil of radius `b(b lt lt a)` and resistance R is moving toward the first coil at a uniform speed v. Find the induced current in smaller coil.
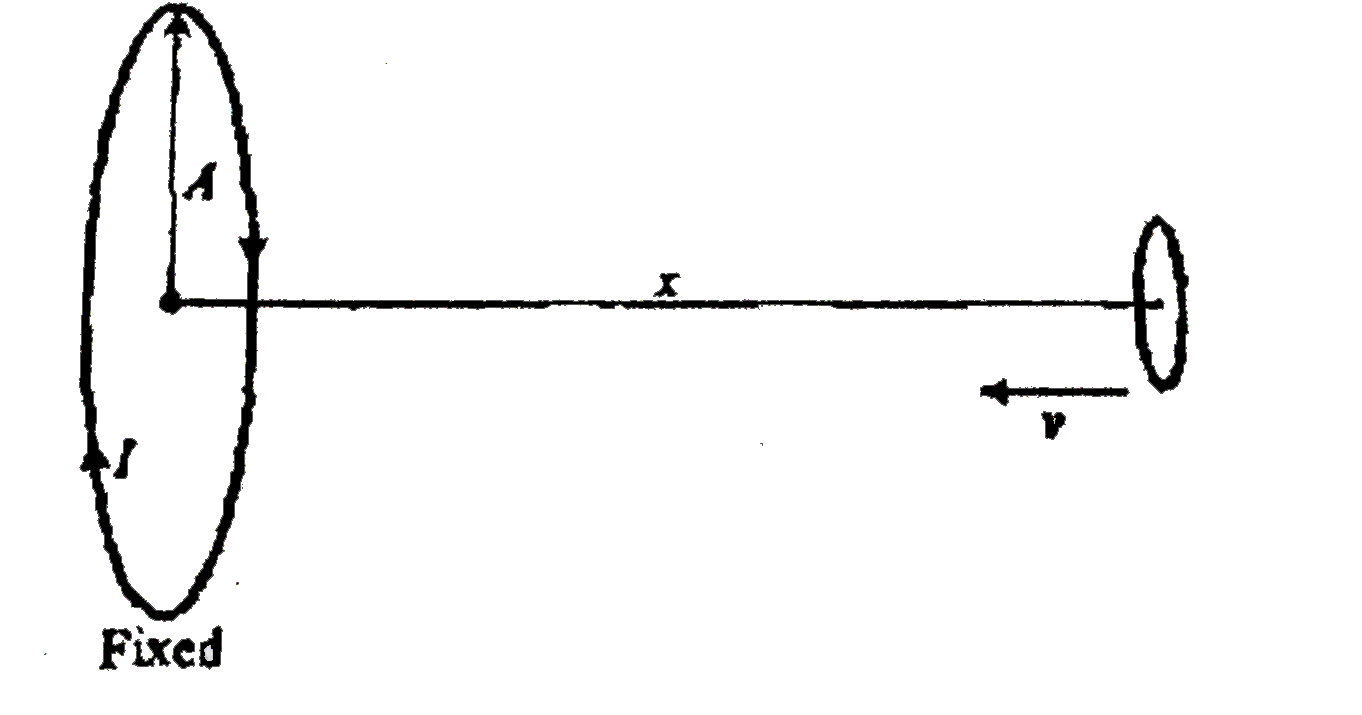 View Solution
View Solution
Practice Exercise 5.2 questions and complete solutions for chapter ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENT of GK PUBLICATIONS PHYSICS (HINGLISH) of Class 12
