Complete Solutions to Illustrative Example of chapter WAVE OPTICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | WAVE OPTICS |
| PHYSICS GALAXY | Illustrative Example |
| Number Of Questions | 33 |
| Academic Year | 2023-24 |
Determine the resulting intensity due to interference of the two waves at a point given below :
`y_(1) = 3 sin (100 pil)`
`y_(2)=4sin(100pil+(pi)/(3))`
Given that intensity due to first wave is `I_(0)`.
View SolutionRadio waves coming at `angle_alpha` to vetical are received by a radar after reflection from a nearby water surface and directly .what should be height of antenna from water surface so that it records a maximum intensity.(Wavelength =`lambda`)
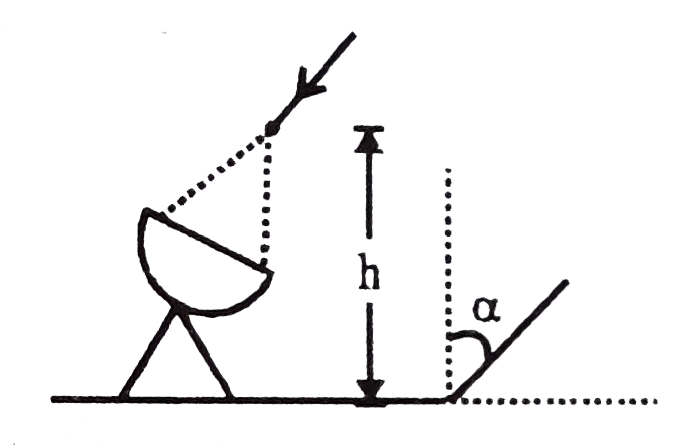
View SolutionTwo coherent light beams of intensities I and 4I superpose in a region. Find the maximum and minimum possible intensities due to superposition in this region.
View SolutionTwo coherent waves are described by the expressions.
`E_(1)=E_(0sin)((2pix_(1))/(lambda)-2pift+(pi)/(6))` and `E_(2)=E_(0)sin((2pix_(2))/(lambda)-2pift+(pi)/(8))`
Determine the relationship between `x_(1)` and `x_(2)` that produces constructive interference when the two waves are superposed?
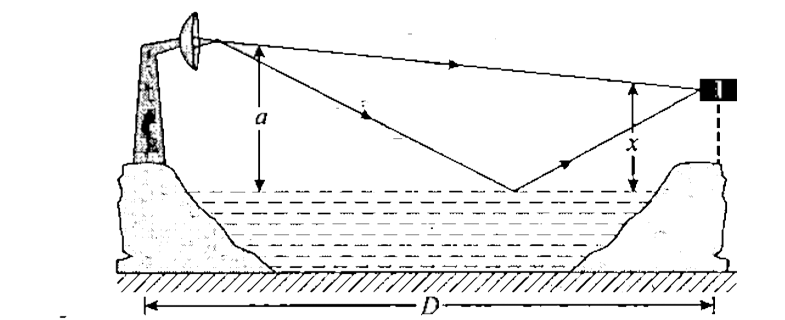
View SolutionIn figure-6.9, a microwave transmitter a height a above the water level of a wide lake transmits microwaves of wavelength `lambda` towards a receiver on the opposite shore, a distance x above the water level. The microwaves reflecting from the water interface with the microwaves arriving directly from the transmitter. Assuming that the lake width D is much greater than a and x, that `lambda gtgt a`, at what values of x is the signal at the receiver maximum?
View SolutionTwo coherent point sources `S_(1)` and `S_(2)` vibrating in phase emit light of wavelength `lambda`. The separation between the sources is `2lambda`. Consider a line passing through `S_(2)` and perpendicular to line `S_(1) S_(2)`. Find the position of farthest and nearest minima.
 .
.
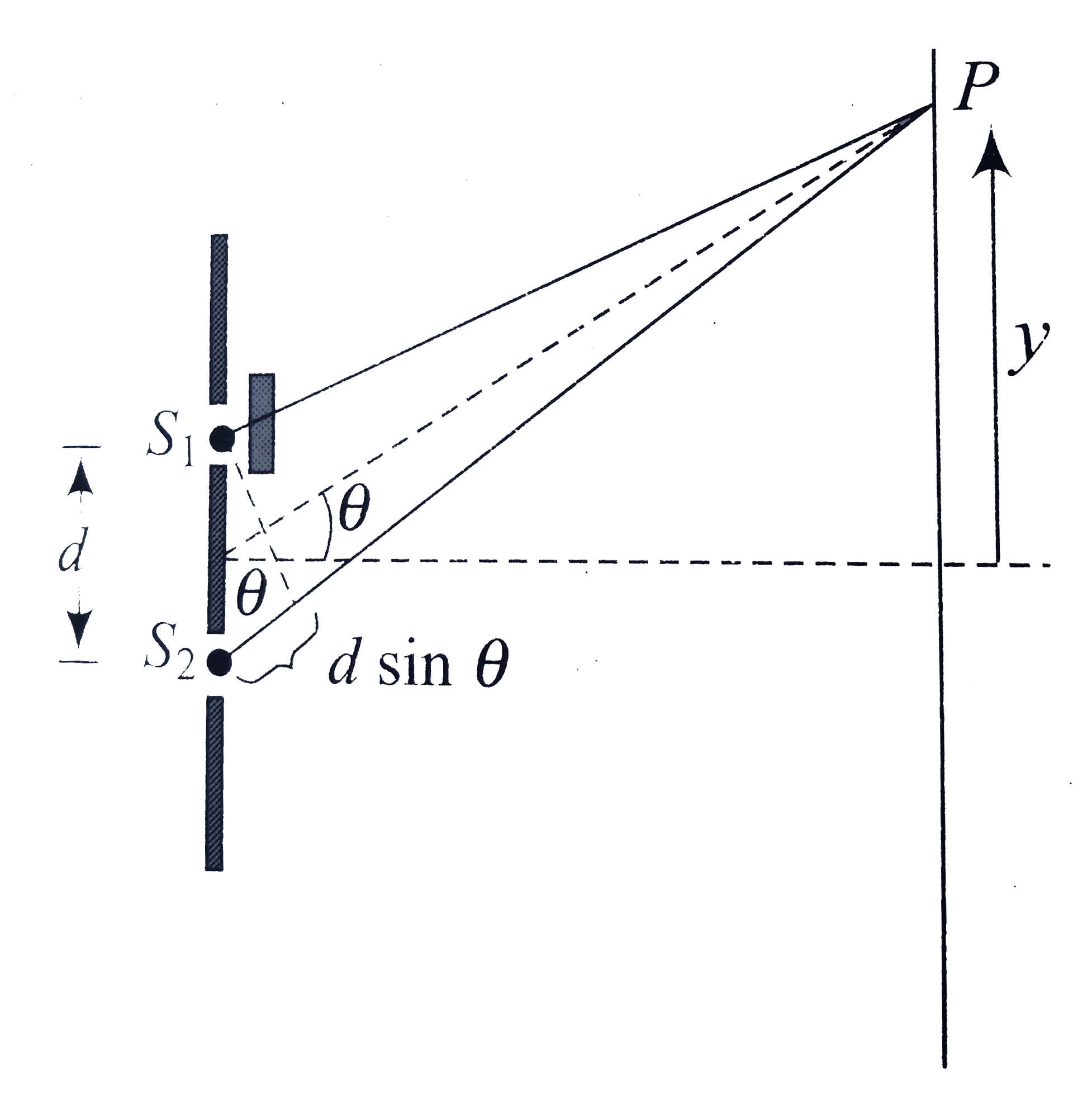
View SolutionA double-slit experiment, arrangement produces interference fringes for sodium light `(lambda = 589 nm)` that have an angular separation of `3.50 xx 0^(-3)` rad . For what wavelength would the angular separation to `10%` greater?
View SolutionIn a YDSE setup sodium light of wavelength `5893 Å` is being used. The interference pattern is obtained on a screen which is located at a distance 1 m from the slit plane. In the interference pattern it is observed that `10^(th)` bright fringe is located at a distance of 12mm from the central maximum. Find the slit separation.
View SolutionTwo slits in Young's experiment have width in the ratio `1 : 25`. The ratio of intensity at the maxima and minima in the interference pattern `(I_(max))/(I_(min))` is :
View SolutionIn Young's experiment, interference bands are produced on the screen placed at 1.5 m from the two slits 0.15 mm apart and illuminated by light of wavelength `6599 Å`. Find (a) the fringe width and (b) the change in the fringe width if the screen is taken away from the slit by 50 cm.
View SolutionIn Young's double slit experiment the slits are 0.5 mm apart and interference is observed on a screen placed at a distance of 100 cm from the slits. It is found that the `9^(th)` bright fringe is at a distance of 8.835 mm from the second dark fringe from the centre of the fringe pattern. Find the wavelength of light used.
View SolutionA double slit arrangement produces interference fringes for sodium light `(lambda = 5890 Å)` that are `0.40^(@)` apart. What is the angular fringe separation if the entire arrangement is immersed in water?
View SolutionA YDSE setup is immersed in water `(mu = 1.33)`. If has slit separation 1 mm and distance between slits and screen is 1.33m. Incident light on slits have wavelength `6300Å`. Find the fringe width on screen.
View SolutionThere are two coherent sources `S_(1)` and `S_(2)` which produce waves in same phase placed on Y axis at points (0, 2d) and (0, d) as shown in figure-6.23. A detector D is placed at origin which moves along X direction, find the number of maxima recorded by detector excluding points x = 0 and `x = oo`. Given that wavelength of light produced is `6200Å` and separation between sources is 0.34 mm.

View SolutionIn YDSE setup slits are illuminated by a light of wavelength `4000Å` and a light of unknown wavelength. It is observed that fourth dark fringe of known wavelength coincide with second bright fringe of unknown wavelength. Find the unknown wavelength.
View SolutionIn YDSE, light of wavelength `lamda = 5000 Å` is used, which emerges in phase from two slits distance `d = 3 xx 10^(-7) m` apart. A transparent sheet of thickness `t = 1.5 xx 10^(-7) m`, refractive index `n = 1.17`, is placed over one of the slits. Where does the central maxima of the interference now appear from the center of the screen? (Find the value of y?)
View SolutionIn Young's experiment, find the distance between two slits that results in the third minimum for `420 nm` violet light at an angle `30^(@)`
 .
.
View SolutionConsider the situation shown in figure-6.35. The two slits `S_(1)` and `S_(2)` placed symmetrically around the central line are illuminated by a monochromatic light of wavelength `lambda`. The separation between the slits is d. The light transmitted by the slits falls on a screen `E_(1)` placed at a distance D from the slits. The slit `S_(3)` is at the central line and the slit `S_(4)` is at a distance z from `S_(3)`. Another screen `E_(2)` is placed a further distance D away from `E_(1)`. Find the ratio of the maximum to minimum intensity observed on `E_(2)` if z is equal is : `(a) (lambdaD)/(2d) " "(b) (lambdaD)/(d)" " (c )(lambdaD)/(4d)`
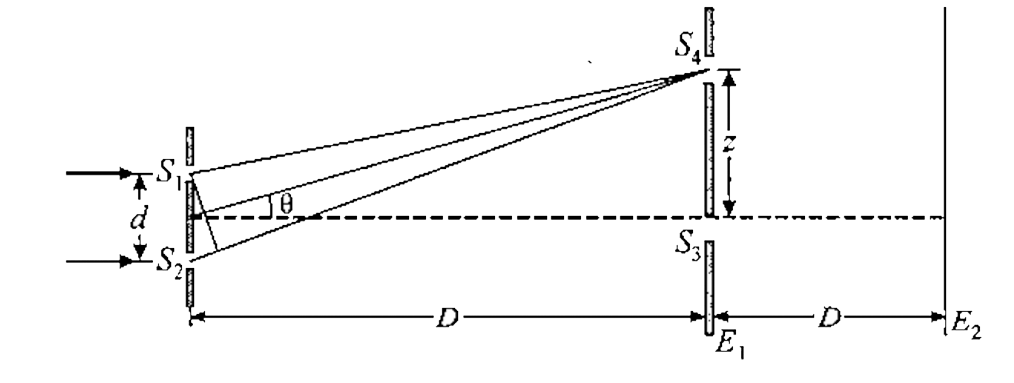
View SolutionThe two coherent sources of monochromatic light of wavelength `lambda` are located at a separation `lambda`. The two sources are placed on a horizontal line and screen is placed perpendicular to the line joining the sources. Find position of the farthest minima from the centre of the sources.
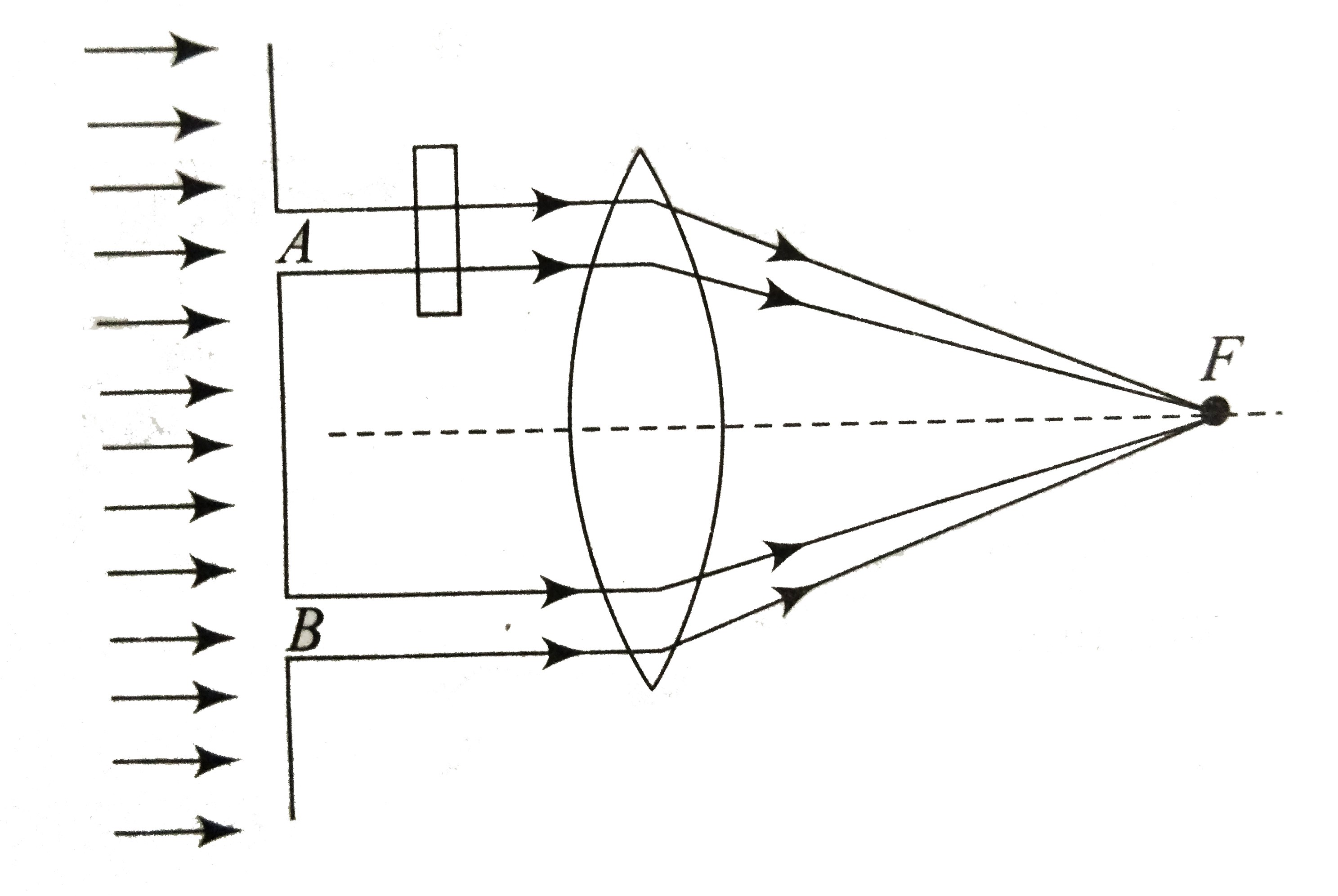
View SolutionIn a modified Young's double-slit experiment, a monochromatic uniform and parallel beam of light of wavelength `6000 Å` and intensity `(10//pi)` W `m^(-2)` is incident normally on two circular apertures A and B of radii 0.001 m and 0.002 m, respectively. A perfectly transparent film of thickness `2000 Å` and refractive index 1.5 for the wavelength of `6000 Å` is placed in front of aperture A (see the figure). Calculate the power (in mW) received at the focal spot F of the lens. Then lens is symmetrically placed with respect to the aperture. Assume that 10% of the power received by each aperture goes in the original direction and is brought to the focal spot.
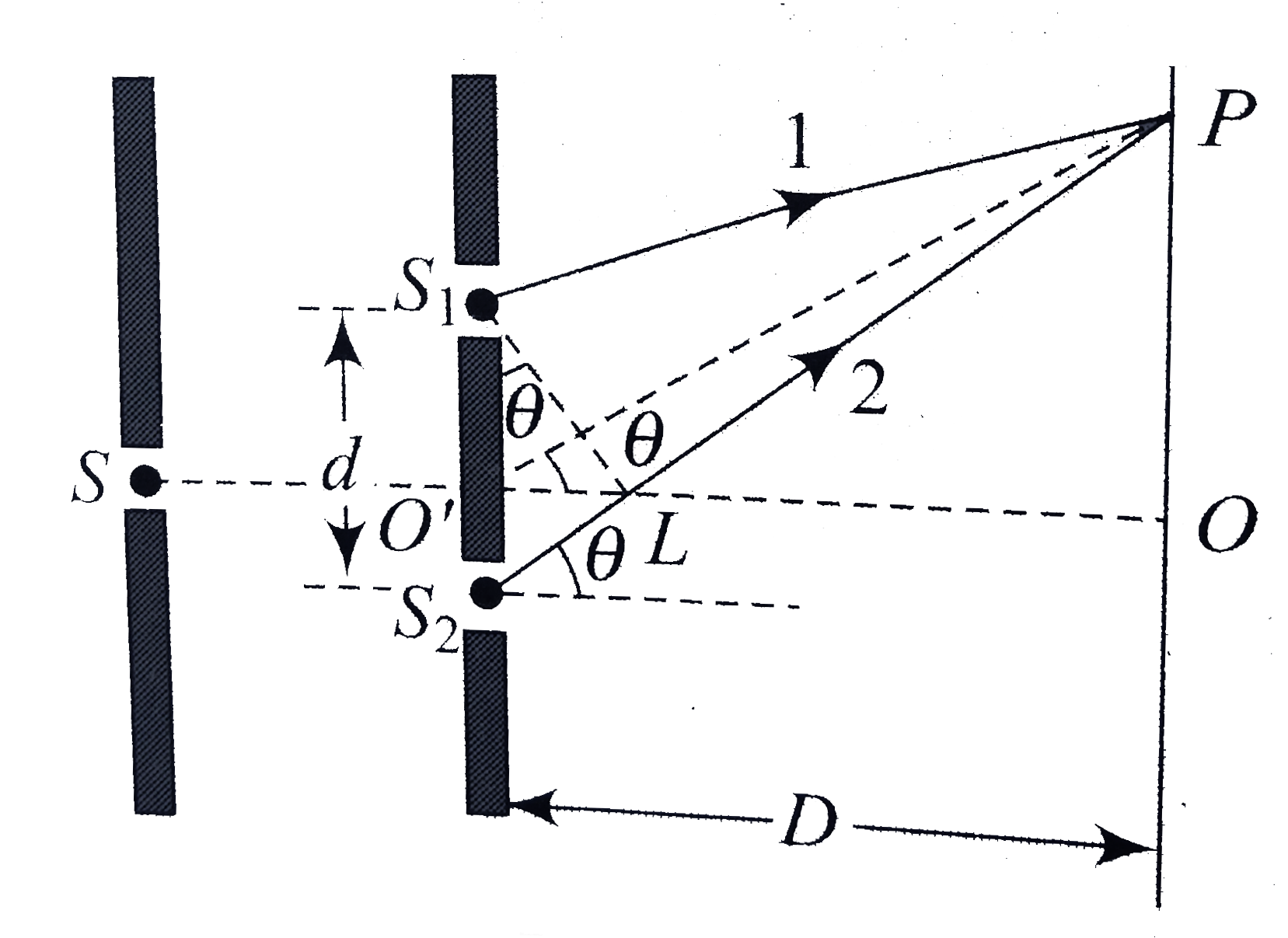
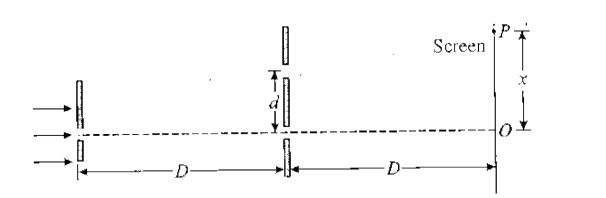
View SolutionConsider the arrangement shown in figure-6.38. The distance D is large compared to the separation d between the slits.
(a) Find the minimum value of d so that there is a dark fringe at O.
(b) Suppose d has this value. Find the distance x at which the next bright fringe is formed.
(c ) Find the fringe width.
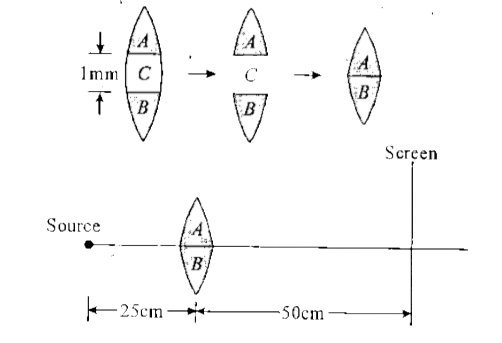
View SolutionIn Billet's Lens Arrangement, a convex lens of focal length 50 cm is cut along the diameter into two indentical halves `Å` and B and in the process a layer C of the lens thickness 1 mm is lost. Then the two halves A and B are put together to form a composite lens. Now, infront of this composite lens a source of light emitting wavelength `lambda = 6000 Å` is placed at a distance of 25 cm as shown in the figure. Behind the lens there is a screen at a distance 50 cm from it. Find the fringe width fo the interference pattern obtained on the screen.
View Solutionfigure shows three equidistant slits illuminated by a monochromatic parallel beam of light. Let `BP_0 -AP_0 = lambda/3` and `Dgtgtlambda`.
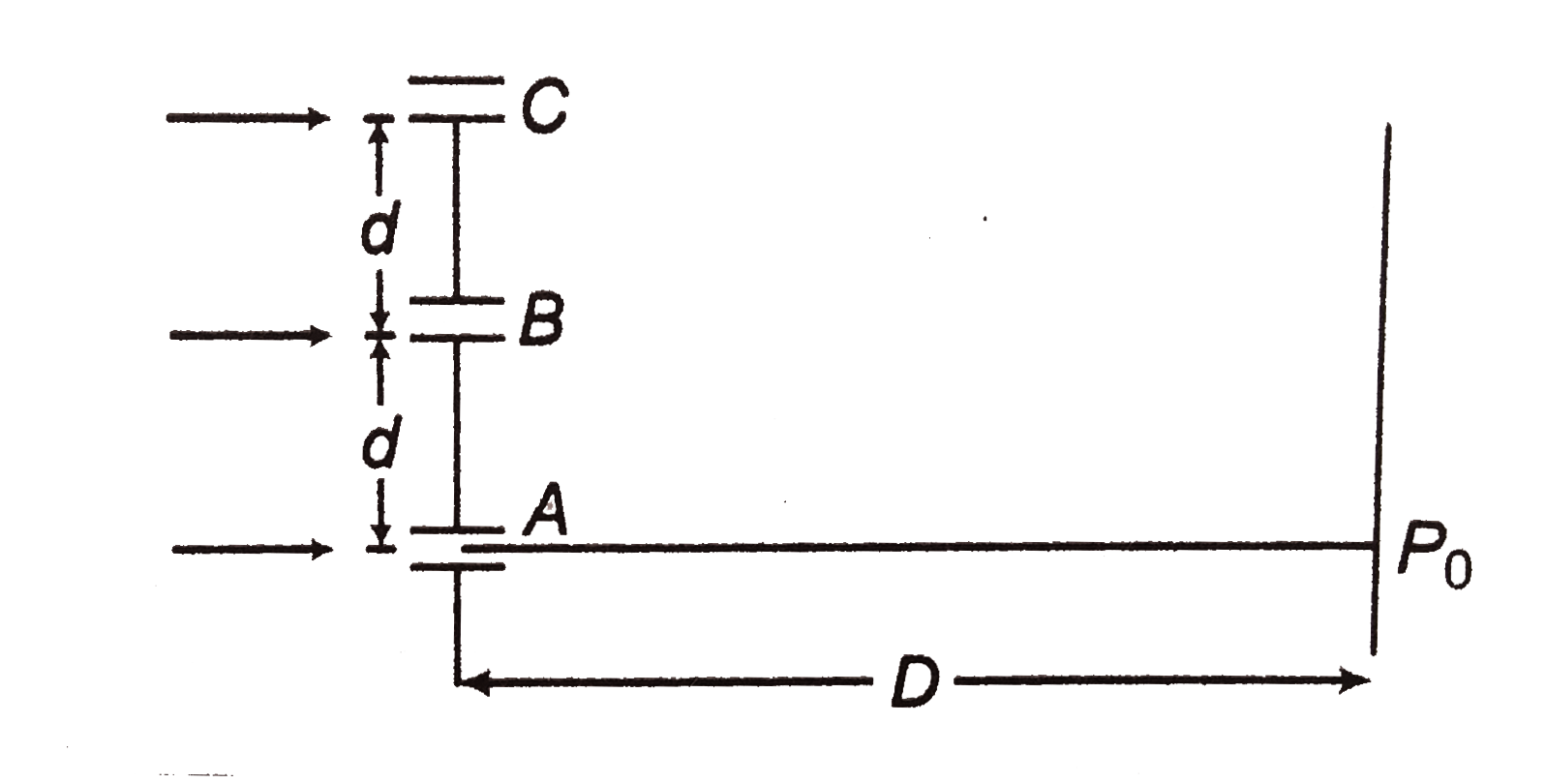
(a) Show that d = `sqrt ((2lambdaD)//3)`
(b) Show that the intensity at `P_0` is three times the intensity due to any of the three slits
individually.
View SolutionA glass lens is coated on one side with a thin film of magnesium fluoride `(MgF_(2))`to reduce reflection from the lens surface (Fig. 2.26). The Index of refraction of `MgF_(2)` is 1.38, that of the glass is 1.50. What is the least coating thickness that eliminates (via interference) the reflections at the middle of the visible specturm `(lambda = 550nm)`? Assume that the light is approxmately perpendicular to the lens surface.
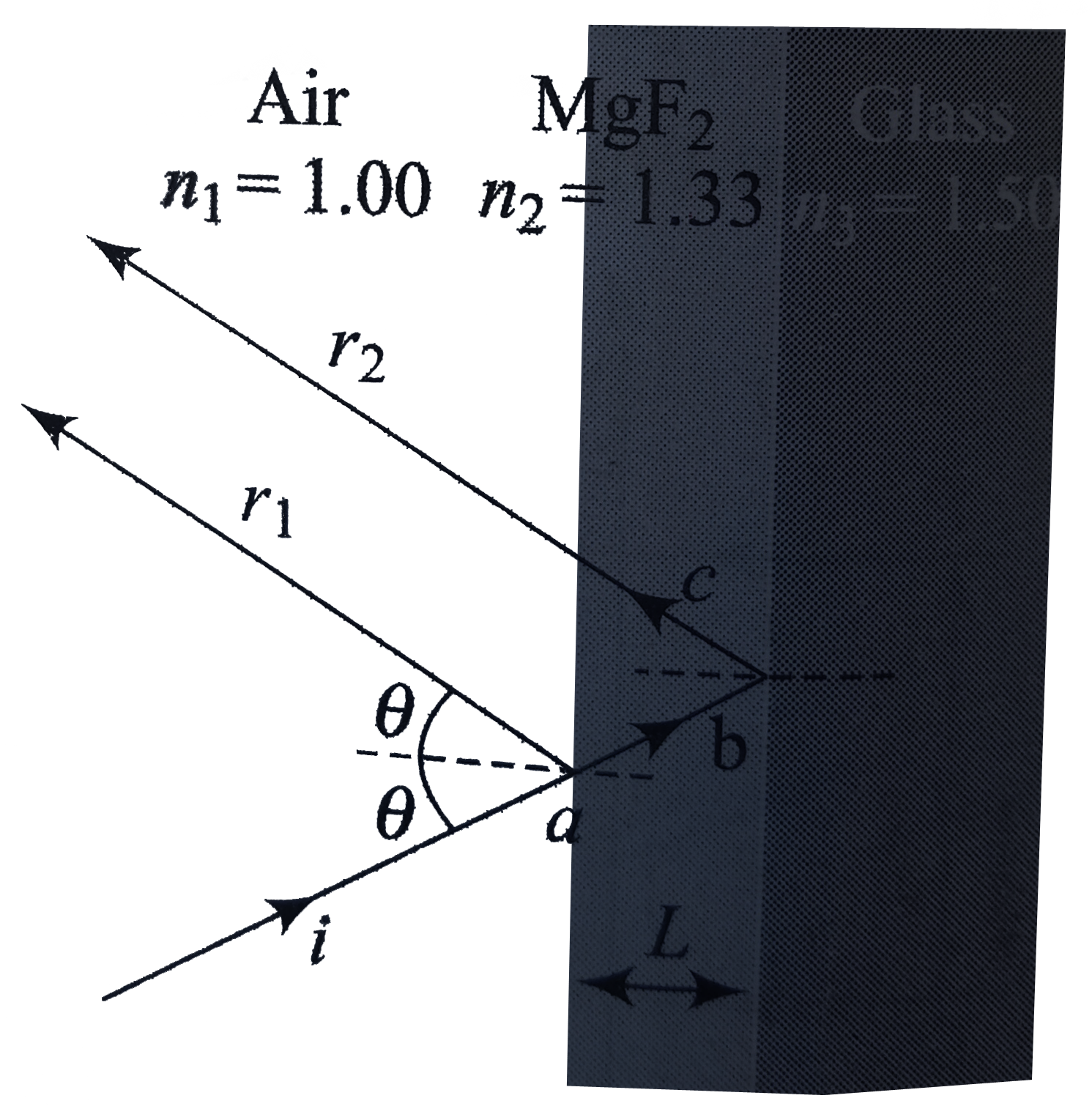
View SolutionRefractive index of a thin soap film of a uniform thickness is 1.34. Find the smallest thickness of the film that gives in interference maximum in the reflected light when light of wavelength `5360 Å` fall at normal incidence.
View SolutionA wedge of angle `0.5^(@)` is illuminated with sodium light whose two lines corresponds to the wavelengths `5890Å` and `5896Å`. Find the distance from the apex at which the maxima due to the two wavelengths first coincide when observed in the reflected light. (the wedge contains air)
View SolutionA broad sources of light of wavelength `680nm` illuminated normally two glass plates.`120nm`long that meet at one end and are separated by a wire`0.048 mm`in diameter at the other end,Find the number of bright fringes formed over the `120nm`distance.

View SolutionA parallel beam of monochromatic light of wavelength `4500Å` is allowed to incident on a long slit of width 0.2 mm. Find the angular divergence in which most of the light is diffracted.
View SolutionAngular width of central maximum in the Fraunhoffer diffraction pattern of a slit is measured. The slit is illuminated by light of wavelength `6000Å`. When the slit is illuminated by light of another wavelength, the angular width decreases by `30%`. Calculate the wavelength of this light. The same decrease in the angular width of central maximum is obtained when the original apparatus is immersed in a liquid. Find the refractive index of the liquid.
View SolutionA convex lens of diameter 8.0 cm is used to focus a parallel beam of light of wavelength 620 nm. If the light be focused at a distance of 20 cm from the lens, what would be the radius of the central bright spot formed ?
View SolutionThe axes of a polarizer and an analyzer are oriented at `30^(@)` to each other.
(a) If unpolarized light of intensity `I_(0)` is incident on them, what is the intensity of the transmitted light?
(b) Polarized light of intensity `I_(0)` is incident on this polarizer-analyzer system. If the amplitude of the light makes an angle of `30^(@)` with the axis of the polarizer, what is the intensity of the transmitted light?
View SolutionA beam of plane polarised light falls normally on a polariser (cross sectional area `3 xx 10^(-4)m^(2)`) which rotates about the axis of the ray with an angular velocity of `31.4 rad//s`. Find the energy of light passing through polariser per revolution and the intensity of emergent beam, if flux of energy of the incident ray is `10^(-3) W`.
View SolutionThe axes of a polarizer and an analyzer are oriented at right angles to each other. A third Polaroid sheet is placed between them with its axis at `45^(@)` to the axes of the polarizer and analyzer.
(a) If unpolarized light of intensity `I_(0)` is incident on this system, what is the intensity of the transmitted light?
(b) What is the intensity of the transmitted light when the middle Polaroid sheet is removed?
View Solution
Illustrative Example questions and complete solutions for chapter WAVE OPTICS of GK PUBLICATIONS PHYSICS (HINGLISH) of Class 12