Complete Solutions to Practice Exercise of chapter WAVE OPTICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | WAVE OPTICS |
| PHYSICS GALAXY | Practice Exercise |
| Number Of Questions | 25 |
| Academic Year | 2023-24 |
In YDSE setup a light of wavelength `6000Å` is used. What should be the separation between the slits so that on screen in front of one of the slit there will be third bright fringe. Take D = 1m.
`[0.6sqrt(10)mm]`
View SolutionA narrow slit S transmitting light of wavelength `lamda` is placed a distance d above a large plane mirror as shown in figure. The light coming directly from the slit and that coming after the reflection interference at a screen `sum` placed at a distance LD from the slit. a. What will be the intensity at a poiint just above the mirror. i.e., just above O? b. At what distance from O does the first maximum occur?
?
View SolutionIn YDSE experiment a uniform intensity light beam is incident on slit plane which has two slits having width ratio `9 : 4`. Find the ratio of intensities of bright and dark fringes on screen.
[25]
View SolutionA vessel ABCD of `10 cm` width has two small slits `S_(1)` and `S_(2)` sealed with idebtical glass plates of equal thickness. The distance between the slits is `0.8 mm`. POQ is the line perpendicular to the plane AB and passing through O, the middle point of `S_(1)` and `S_(2)`. A monochromatic light source is kept at `S, 40 cm` below `P` and `2 m` from the vessel, to illuminate the slits as shown in the figure. Calculate the position of the central bright fringe on the other wall CD with respect of the line `OQ`. Now, a liquid is poured into the vessel and filled up to `OQ`. The central bright fringe is fiund to be at Q. Calculate the refractive index of the liquid.

View SolutionIn a YDSE setup a parallel light beam containing two wavelength `4000 Å` and `5600 Å` is allowed to incident at an angle `30^(@)` on a diaphragm having two narrow slits at a separation 2 mm as shown in figure-6.46. The screen is placed at a distance 40 cm from the slits. A mica film of thickness 5 mm is placed in front of one of the slits and the whole apparatus is submerged in water. If the central bright fringe is observed at point C, which is equidistant from both the slits. Calculate
(a) The refractive index of the slab.
(b) The distance of the first black line from C.

[(a) 1.6, (b) 210 `mum`]
View SolutionA monochromatic light of wavelength `5000Å` incident normally on slit plane of YDSE setup. If `d = 5 xx 10^(-4)m` and D = 1 m and a thin film thickness `1.5 xx 10^(-6)m` and `mu = 1.5` is place in front of one of the slits, find intensity of light at the centre of screen if each slit produces an intensity `I_(0)` on screen. [0]
View SolutionTwo transparent sheets of thickness `t_(1)` and `t_(2)` and refractive indexes `mu_(1)` and `mu_(2)` are placed infront of the slits in YDSE setup as shown in figure-6.47. If D is the distance of the screen from the slits, then find the distance of zero order maxima from the centre of the screen. What is the condition that zero order maxima is formed at the centre O?

`[(D[(mu_(1)-1)t_(1)-(mu_(2)-1)t_(2)])/(d),(mu_(2)-1)t_(2)]`
View SolutionA Lloyd's mirror or length 5 cm is illuminated with mon ochromatic light of wavelength `lambda (= 6000 Å)` from a narrow 1 mm slit in its plane and 5 cm plane from its near edge. Find the fringe width on a screen 120 cm from the slit and width of interference pattern on the screen.

View SolutionIn figure S is a monochromatic point source emitting light of wavelength `lambda=500 nm`. A thin lens of circular shape and focal length `0.10 m` is cut into two identical halves `L_(1)` and `L_(2)` by a plane passing through a doameter. The two halves are placed symmetrically about the central axis `SO` with a gap of `0.5 mm`. The distance along the axis from `A` to `L_(1)` and `L_(2)` is `0.15 m`, while that from `L_(1)` and `L_(2)` to `O` is `1.30 m`. The screen at `O` is normal to `SO`.
(a) If the `3^(rd)` intensity maximum occurs at point `P` on screen, find distance `OP`.
(b) If the gap between `L_(1)` and `L_(2)` is reduced from its original value of `0.5 mm`, will the distance `OP` increases, devreases or remain the same?

View SolutionIn Young's experiment, the source is red light of wavelength `7xx10^(-7)m`. When a thin glass plate of refractive index `1.5` at this wavelength is put in the path of one of the intering beams, the central bright fringe shiffts by `10^(-3)m` to the position previously occupied by the `5^(th)` bright fringe.
When the source is now changed to green light of wavelength `5xx10^(-7)m`, the central fringe shifts to position initially occupied by the `6^(th)` bright fringe to red light. Find the refractive index of glass for green light.
View SolutionIn Young’s double slit experiment, the upper slit is covered by a thin glass plate of refractive index 1.4 while the lower slit is covered by another glass plate having same thickness as the first one but having refractive index 1.7.
Interference pattern is observed using light of wavelength` 5400overset(@)A`. It is found that the point P on the screen where the central maximum fell before the glass plates were inserted, now has ` 3/ 4` the original intensity. It is also observed that what used to be `5^(th)` maximum earlier, lies below the point P while the`6_(th)` minimum lies above P. Calculate the thick- ness of glass plates. Absorption of light by glass plate may be neglected.
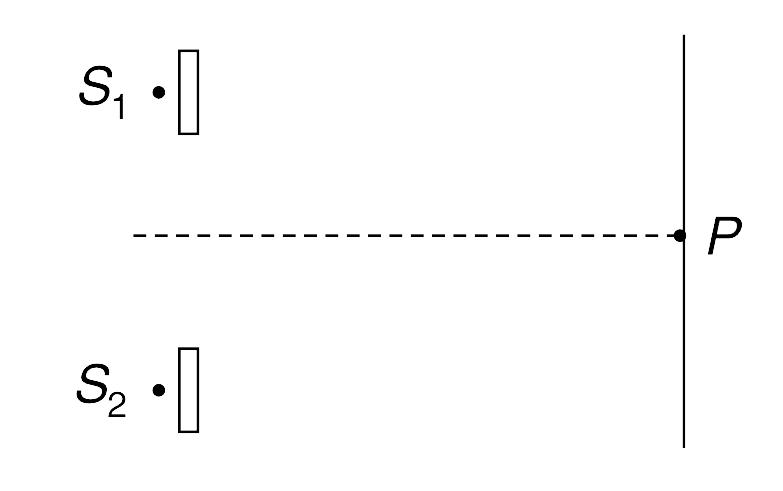
View SolutionA coherent parallel beam of microwaves of wavelength `lambda = 0.5 mm` falls on aYoung's double- slit apparatus. The separation between the slits is 1.0 mm. The intensity of microwaves is measured on a screen placed parallel to the plane of the slits at a distance of 1.0 m from it as shown in Fig. 2.42.
If the incident beam makes an angle or `30^(@)` with the x-axis (as in the dotted arrow shown in the figure), find the y-coordinates of the first minima on either side of the central maximum.
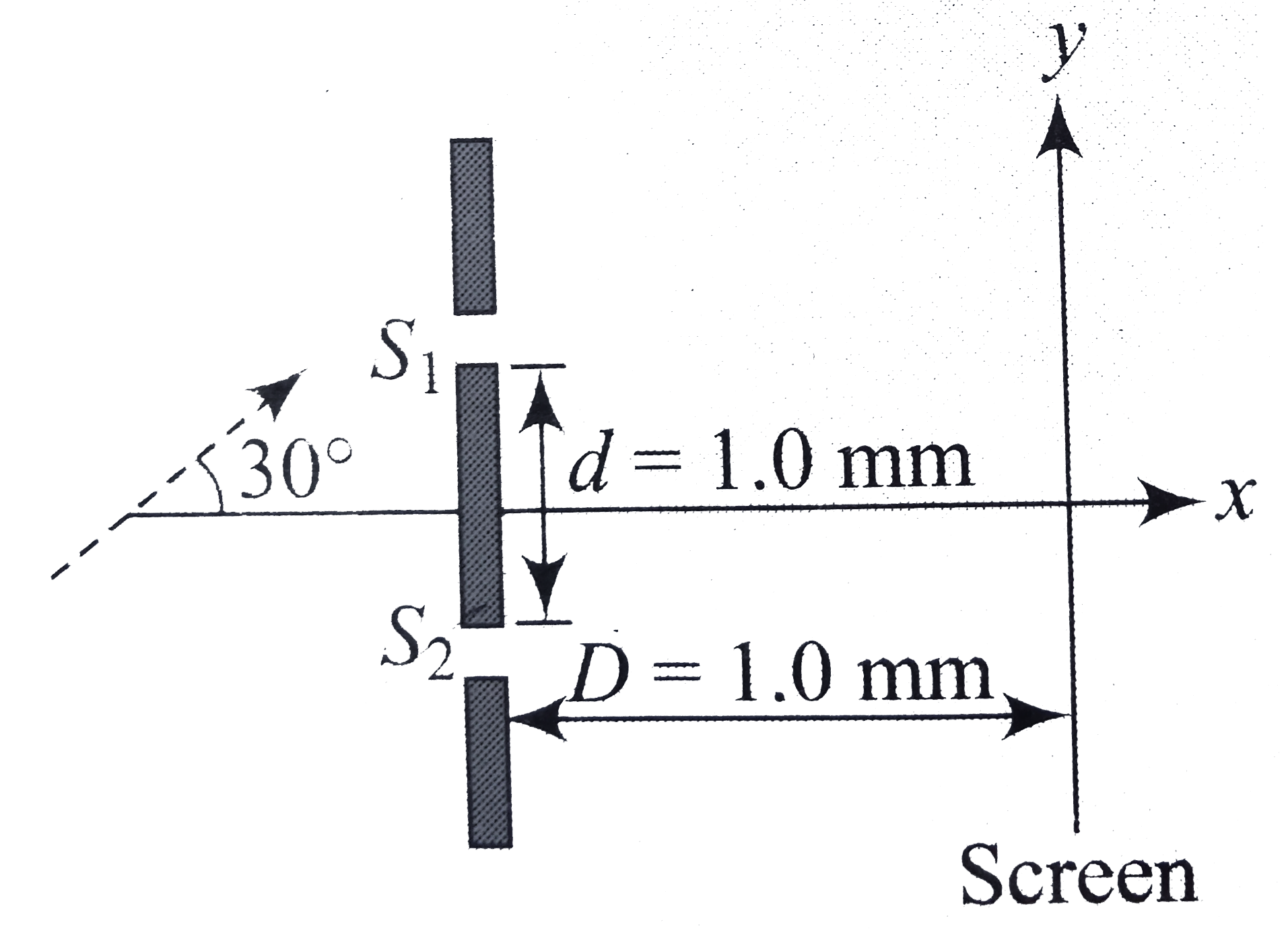
View SolutionA slit of width d is illuminated by white light (which consists of all the wavelengths in the visible range).
(a) For what value of d will the first minimum for red light of wavelength `lambda = 6500Å` appear at `theta = 15^(@)` ?
(b) What is the wavelength `lambda` of the light whose first side diffraction maximum is at `15^(@)`, thus coinciding with the first minimum for the red light?
`[(a) 2.5 mu m, (b) 4300Å]`
View SolutionOur disscusssion of the techniques for determining cosntructive and destructive by reflection from a thin film in air has been confused to rays striking the film a nearly the normal incidence.Assume that a ray is incident at an angle of `45^(@)` (relative to the normal ) on a film with an index of refraction of `sqrt(2)`.Calculate the minimum thickness fro constructive interference for light of wavelength `600nm`.
View SolutionA soap film of thickness 0.0011 mm appears dark when seen by reflected light of wavelength `5800Å`. What is the refractive index of soap solution if it is between 1.2 and 1.5. `[mu = 1.318]`
View SolutionA wedge-shaped film of air is produced by placing a fine wire of diameter D between the ends of two flat glass plates of length `L = 20 cm`, as shown in the figure-6.68. When the air film is illuminated with light of wavelength `lambda = 5500Å`, there are 12 dark fringes found per centimeter on the wedge. Find the wire diameter D.
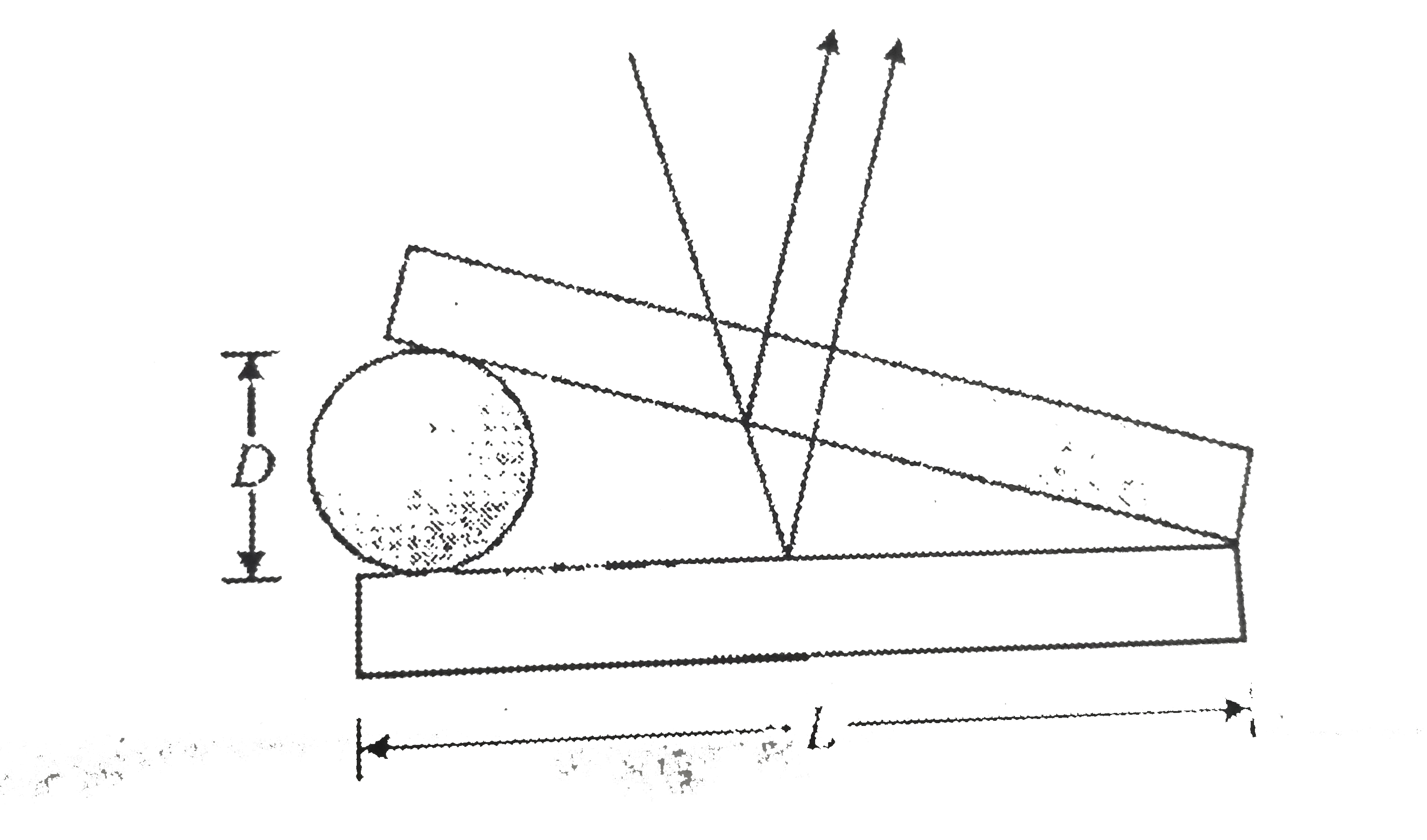
`[6.6 xx 10^(-5)m]`
View SolutionA thin soap film of thickness `3 xxx 10^(-7)m` and `mu = 1.5` is spreaded on a glass surface. When white light is normally incident on this sheet, find the colour which will be reflected strongly by the film.
`[4500Å]`
View Solution_E01_093_Q01.png)
A ray light of intensity I is incident on a parallel glass-slab at a point A as shown in figure it undergoes partial reflection and refraction. At each reflection 20% of incident energy is refracted rays AB and A'B' undergo interference find the ratio `I_(max)//I_(min)`
View SolutionA point sources `S` emitting light of wavelength `600nm` is placed at a very small height `h` above the flat reflecting surface `AB`(see figure).The intensity of the reflected light is`36%` of the intensity.interference firnges are observed on a screen placed parallel to the reflecting surface a very large distance `D` from it.
(A)What is the shape of the interference fringes on the screen?
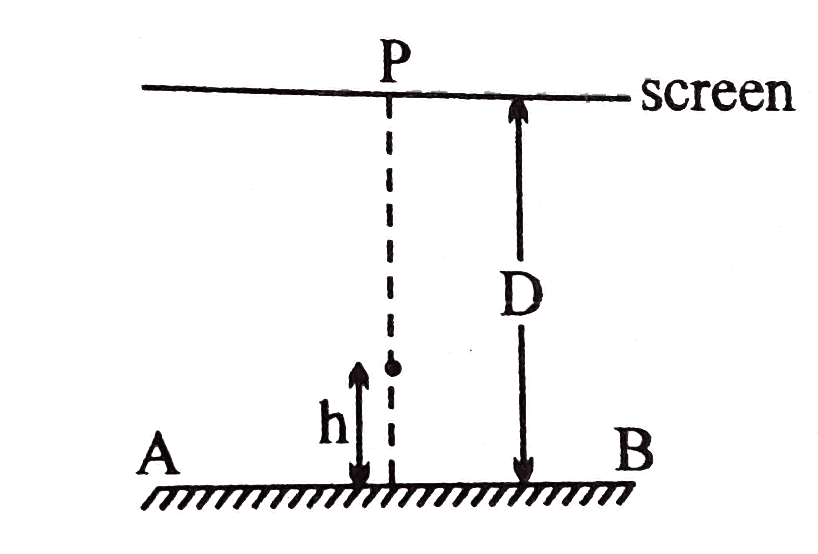
(B)Calculate the ratio of the minimum to the maximum to the maximum intensities in the interference fringes fromed near the point `P` (shown in the figure) (c) if the intenstities at point `P` corresponds to a maximum,calculate the minimum distance through which the reflecting surface `AB` should be shifted so that the intensity at `P` again becomes maximum.
View SolutionA slit is located 'at infinity' in front of a lens of focal length 1 m and is illuminated normally with light of wavelength `6000Å`. The first minima on either side of the central maximum of the diffraction pattern observed in the focal plane of the lens are separated by 4 mm. What is the width of the slit?
[0.3 mm]
View SolutionFrom large distance microwaves fall on a long slit of width 5cm. If the first diffraction minima is obtained at an angle `30^(@)` form the direct vision slit line then find the wavelength of the microwaves.
[2.5 cm]
View SolutionA parallel beam of monochromatic light of wavelength `5900Å` falls normally on a convex lens of diameter 10cm which focusses the light on a flat normal screen located at a distance of 20cm from the lens. What would be the radius of the central bright spot formed on the screen?
View SolutionThree nicols prisms are placed such that, first and third are mutually perpendicular. Unpolarised light is incident on first nicol's prism, the intensity of light emerges from third nicol's prism is `1//16` the intensity of incident light. Find the angle between first and second nicol's prisms.
`[22.5^(@)]`
View SolutionPolarized light of intensity `I_(0)` is incident on a pair of Polaroid sheets. Let `theta_(1)` and `theta_(2)` be the angles between the incident amplitude and the axes of the first and second sheet, respectively. Show that the intensity of the transmitted light is `I=I_(0)cos^(2)theta_(1)cos^(2)(theta_(1)-theta_(2))`.
View SolutionA mixture of plane polarised and unpolarised light falls normally on a polarising sheet. On rotating the polarising sheet about the direction of the incident beam, the transmitted intensity varies by a factor 4. Find the ratio of the intensities `I_(P)` and `I_(0)` respectively of the polarized and unpolarised components in the incident beam. Next the axis of polarising sheet is fixed at an angle of `45^(@)` with the direction when the transmitted intensity is maximum. Then obtain the total intensity of the transmitted beam in terms of `I_(0)`.
`[(3)/(2),(5I_(0))/(4)]`
View Solution
Practice Exercise questions and complete solutions for chapter WAVE OPTICS of GK PUBLICATIONS PHYSICS (HINGLISH) of Class 12