Complete Solutions to Advance MCQs with One or More Options Correct of chapter WAVES of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | WAVES |
| PHYSICS GALAXY | Advance MCQs with One or More Options Correct |
| Number Of Questions | 30 |
| Academic Year | 2023-24 |
A sound wave propagates in a medium of Bulk's modulus B by means of compressions and rarefactions. If `P_(c)` and `P_(r)` are the pressures at compression and rarefaction respectively,a be the wave amplitude and k be the angular wave number then
View SolutionA driver in a stationary car blows a horn which produces monochromatic sound waves of freqeuncy 1000 Hz normally towards a reflecting wall. The wall approaches the car with a speed of `3.3(m)/(s)`.
View SolutionThe equation of a wave is
`y=4 sin[(pi)/(2)(2t+(1)/(8)x)]`
where y and x are in centimeres and t is in seconds.
View SolutionA sinusoidal wave `y_(1) = a sin ( omega t - kx) ` is reflected from a rigid support and superpose with the incident wave `y_(1)` . Assume the rigid support to be at `x = 0`.
View Solution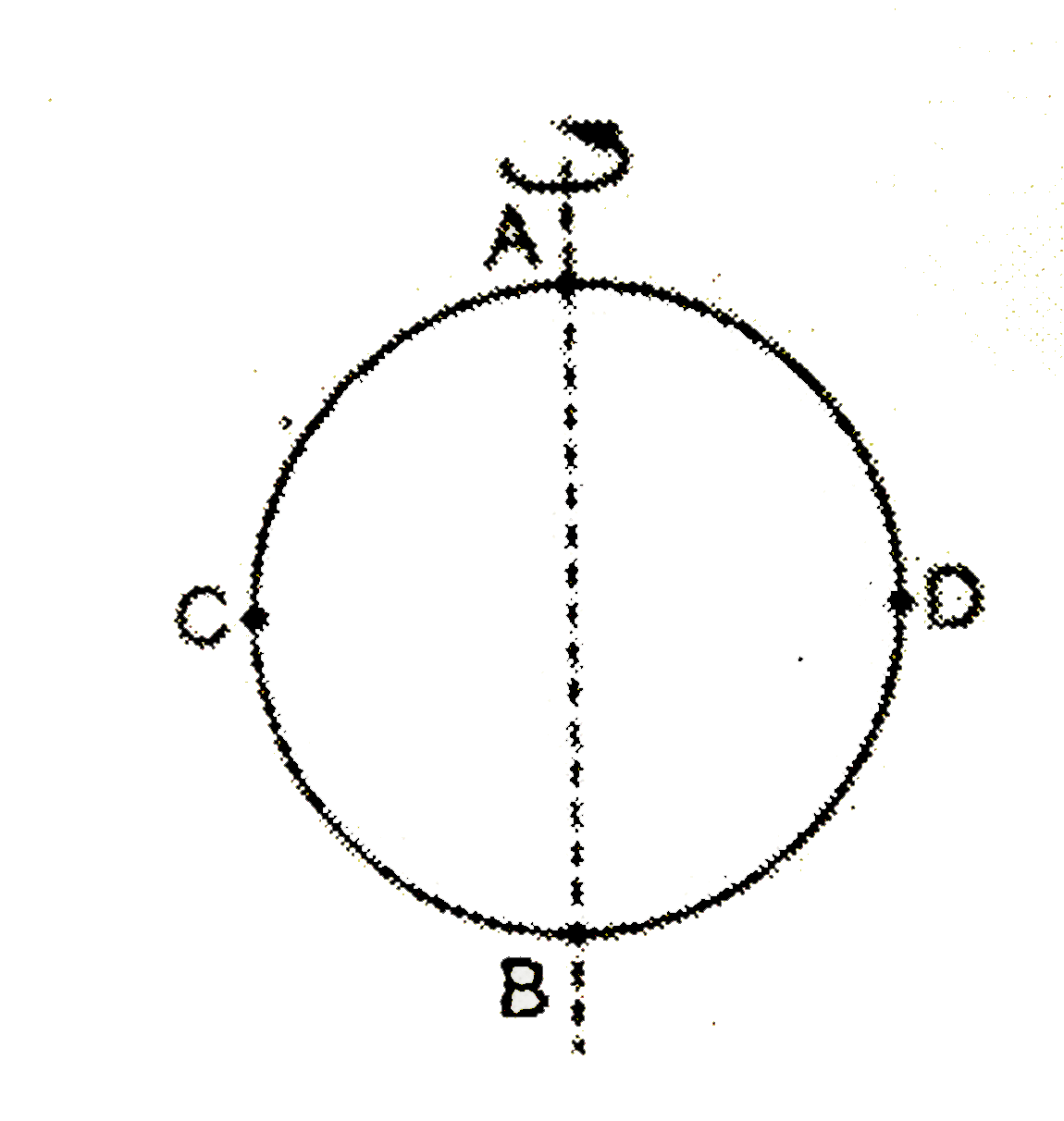
Assume that the sun rotates about an axis through its centre and perpendicular to the plane of rotatin of the earth about the sun. The appearange of the sun, from any one pont on the earth, is shown. Light belonging to a particular spectral line, as received from the points `A, B, C` and `D` on the edge of the sun, are analyzed
View SolutionWhen the open organ pipe resonates in its fundamental mode then at the centre of the pipe
View Solution`y(x, t) = 0.8//[4x + 5t)^(2) + 5]` represents a moving pulse, where `x` and `y` are in meter and `t` in second. Then
View SolutionIn a wave motion `y = a sin (kx - omegat)`, `y` can represent
View SolutionA travelling wave in a stretched string is described by the equation `y = A sin (kx - omegat)` the maximum particle velocity is
View SolutionIn Q.No. 6-9
View SolutionAs a wave propagates
View SolutionAny progressive wave equationin differential form is :
View SolutionTwo waves of nearly same amplitude , same frequency travelling with same velocity are superimposing to give phenomenon of interference . If `a_(1)` and `a_(2)` be their respectively amplitudes , `omega` be the frequency for both , `v` be the velocity for both and `Delta phi` is the phase difference between the two waves then ,
View SolutionTwo waves of slightly different frequencies `f_(1) and f_(2) (f_(1) gt f_(2))` with zero phase difference , same amplitudes ,travelling in the same direction superimpose .
View SolutionThe displacement of a particle in a medium due to a wave travelling in the `x-`direction through the medium is given by `y = A sin(alphat - betax)`, where `t =` time, and `alpha` and `beta` are constants:
View SolutionA wave is represented by the equation
`y = A sin(10pix + 15pit + (pi)/(3))`
where `x` is in meter and `t` is in seconds. The expression represents :
View SolutionConsider a harmonic wave travelling on a string of mass per unit length p.The wave has a velocity v, amplitude A and frequency f The power transmitted by a harmonic wave on the string is proportional to (take constant of proportionality as `2pi^(2)`
View SolutionStanding waves can be produced
View SolutionFor a sine wave passing through a medium, let y be the displacement of a particle, v be its velocity and a be its acceleration :-
View SolutionP,Q and R are three particle of a medium which lie on the x-axis. A sin wave of wavelength `lamda` is travelling through the medium in the x-direction. P and Q always have the same speed. Whilem P and R always have the same velocity. The minimum distance between :-
View Solutiontransverse simple harmonic wave is travelling on a string. The equation of the wave:
View SolutionA sound waves passes from a medium `A` to a medium `B`. The velocity of sound in `B` is greater than in `A`. Assume that there is no absorption or reflection at the boundary . As the wave moves across the boundary :
View SolutionIn a stationary wave system, all the particles of the medium
View SolutionIn the previous Q.No. 6-23, all the particles:
View SolutionTwo simple harmonic waves are represented by the equations given as
`y_(1) = 0.3 sin(314 t - 1.57 x)`
`y_(2) = 0.1 sin(314 t - 1.57x + 1.57)`
where `x, y_(1)` and `y_(2)` are in metre and t is in second, then we have
View SolutionTwo waves `y_(1) = a sin (omegat - kx)` and `y_(2) = a cos(omegat - kx)` superimpose at a point :
View SolutionPlane harmonic waves of frequency 500 Hz are produced in air with displacement amplitude of `10mum`. Given that density of air is `1.29(kg)/(m^3)` and speed of sound in air is `340(m)/(s)`. Then
View SolutionTwo waves travelling in opposite directions produce a standing wave . The individual wave functions are given by `y_(1) = 4 sin ( 3x - 2 t)` and `y_(2) = 4 sin ( 3x + 2 t) cm` , where `x` and `y` are in cm
View SolutionTwo waves travelling in a medium in the x-direction are represented by `y_(1) = A sin (alpha t - beta x)` and `y_(2) = A cos (beta x + alpha t - (pi)/(4))`, where `y_(1)` and `y_(2)` are the displacements of the particles of the medium `t` is time and `alpha` and `beta` constants. The two have different :-
View SolutionVelocity of sound in air is
View Solution
Advance MCQs with One or More Options Correct questions and complete solutions for chapter WAVES of GK PUBLICATIONS PHYSICS (HINGLISH) of Class 12
All Exercises from PHYSICS GALAXY Class 12 PHYSICS WAVES
- Advance MCQs with One or More Options Correct
- Conceptual MCQs Single Option Correct
- Discussion Question
- Illustrative
- Numerical MCQs Single Options Correct
- Practice Exercise 6.1
- Practice Exercise 6.2
- Practice Exercise 6.3
- Practice Exercise 6.4
- Practice Exercise 6.5
- Practice Exercise 6.6
- Practice Exercise 6.7
- Practice Exercise 6.8
- Unsolved Numerical Problems for Preparation of NSE, INPhO & IPhO