Complete Solutions to Numerical MCQs Single Options Correct of chapter WAVES of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | WAVES |
| PHYSICS GALAXY | Numerical MCQs Single Options Correct |
| Number Of Questions | 90 |
| Academic Year | 2023-24 |
A man sets his watch by the sound of a siren placed at a distance 1 km away . If the velocity of sound is `330 m//s`
View SolutionThe frequency of a tunning fork is 384 per second and velocity of sound in air is 352 m/s . How far the sound has traversed while fork completes 36 vibration
View SolutionThe equation of displacement of two waves are given as
` y_(1) = 10 sin( 3 pi t + (pi)/(3)) , y_(2) = 5 [ sin 3 pi t + sqrt(3) cos 3 pi t]`
Then what is the ratio of their amplitudes
View SolutionConsider ten identical sources of sound. All giving the same frequency but having phase angles which are random.If the average intensity of each source is ` I_0 ` the average of resultant intensity I due to all these ten sources will be
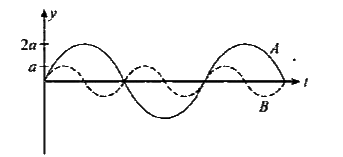
View SolutionThe displacement-time graphs for two sound waves A and 5 are shown in the figure-6.98, then the ratio oftheir intensities `I_(A)//I_(B)` is equal to:
View SolutionA tuning fork of frequency 340 Hz is vibrated just above the tube of 120 cm height. Water is poured slowly in the tube. What is the minimum height of water necessary for the resonance? (speed of sound in the air = 340m/s)
View SolutionTwo monoatomic ideal gases 1 and 2 of molecular masses `m^(1)` and `m^(2)` respectively are enclosed in separate containers kept at the same temperature. The ratio of the speed of sound in gas 1 to that in gas 2 is given by :-
View SolutionAn organ pipe is closed at one end has fundamental frequency of 1500 Hz. The maximum number of overtones generated by this pipe which a normal person can hear is
View SolutionThe speed of a wave in a medium is 760 m/s. If 3600 waves are passing through a point in the medium in 2 min, then their wavelength is
View SolutionA tuning fork sounded together with a tuning fork of frequency 256 emits two beats. On loading the tuning fork of frequency 256, the number of beats heard are 1 per second. The frequency of tuning fork is
View Solution(a) The power of sound from the speaker of a radio is 20 mW. By turning the knob of volume control the power of sound is increased to 400 mW, What is the power increase in dB as compared to original power? (b) How much more intense is an 80 dB sound than a 20 dB whisper?
View SolutionIn the experiment for the determination of the speed of sound in air using the resonance column method, the length of the air column that resonates in the fundamental mode, with a tuning fork is `0.1m`. When this length is changed to `0.35m`, the same tuning fork resonates with the first overtone. Calculate the end correction.
View SolutionAn observer moves towards a stationary source of sound, with a velocity one-fifth of the velocity of sound. What is the percentage increase in the apparent frequency?
View SolutionThe intensity of sound from a radio at a distance of 2 metres from its speaker is `1xx0^(-2) mu W//m^(2)`. The intensity at a distance of 10 meters would be
View SolutionA closed organ pipe of length `L` and an open organ pipe contain gass of densities `rho_(1)` and `rho_(2)`, respectively. The compressibility of gass are equal in both the pipes. Both the pipes are vibrating in their first overtone with same frequency . The length of the open orange pipe is
(a) `(L)/(3)`
`(4l) / (3)`
(c ) `(4l)/(3)sqrt((rho_(1))/(rho_(2)))`
(d) `(4l)/(3)sqrt((rho_(2))/(rho_(1)))`
View SolutionIn Melde's experiment, the string vibrates in 4 loops when a 50 gram weight is placed in the pan of weight 15 gram . To make the string to vibrates in 6 loops the weight that has to be removed from the pan is
View SolutionThe displacement of a wave disturbance propagating in the positive x-direction is given by
`y =(1)/(1 + x^(2))`at `t = 0` and `y =(1)/(1 +(x - 1)^(2))` at `t =2s`
where, `x` and `y` are in meter. The shape of the wave disturbance does not change during the propagation. what is the velocity of the wave?
View SolutionThe equation of a progressive wave is given by
`y=a sin (628 t-31.4 x)`
If the distances are expressed in cms and time in seconds, then the wave velocity will be
View SolutionTwo waves are approaching each other with a velocity of `20m//s` and frequency `n`. The distance between two consecutive nudes is
View SolutionConsider the three waves `z_(1), z_(2) "and" z_(3)` as
`z_(1) = A "sin"(kx - omega t)`
`z_(2) = A "sin"(kx + omega t)`
`z_(3) = A "sin"(ky - omega t)`
Which of the following represents a standing wave?
View SolutionEquation of a progressive wave is given by `y= a sin pi [(t)/(2)-(x)/(4)]`, where t is in seconds and x is in meters. The distance through which the wave moves in 8 sec is (in meter)
View SolutionThe phase difference between two waves represented by `y_(1)=10 ^(-6) sin [100 t+(x//50)+0.5]m, y_(2)=10^(-6) cos[100t+(x//50)]m`where x is expressed in metres and t is expressed in seconds, is approximately
View SolutionTwo waves are given by`y_(1) = a sin (omega t - kx)` and `y_(2) = a cos (omega t - kx)`. The phase difference between the two waves is
View SolutionTwo identical sonometer wires have a fundamental frequency of `500 Hz` when kept under the same tension . The percentage change in tension of one of the wires that would cause an occurrence of `5 beats//s` , when both wires vibrate together is
View SolutionA source of sound is travelling towards a stationary observer. The frequency of sound heard by the observer is of three times the original frequency. The velocity of sound is v m / sec . The speed of source will be
View SolutionA tuning fork of frequency 480 Hz produces 10 beats per second when sounded with a vibrating sonometer string. What must have been the frequency of the string if a slight increase in tension produces lesser beats per second than before
View SolutionA string is producing transverse vibration whose equation is y = 0.021 sin ( x + 30 t ) , where x and y are in metre and t is in second . If the linear density of the string is `1.3xx10^(-4)kg//m` , then tension in string in newton will be
View SolutionIn a large room, a person receives direct sound waves froma source 120 metres away from him. He also receives waves from the same source which reach him, being reflected from the 25 metre high ceiling at a point halfway between them. The two waves interfere constuctively for wavelength of
View SolutionA sound source is moving towards a stationary observer with 1/10 of the speed of sound. The ratio of apparent to real frequency is
View SolutionA string of length `0.4 m` and mass `10^(-2)kg` is tightly clamped at its ends. The tension in the string is `1.6 N`. Identical wave pulse are produced at one end at equal intervals of time, `Deltat`. The minimum value of `Deltat` which allows constructive interference of successive pulse is
View SolutionAn earthquake generates both transverse (S) and longitudinal (P) sound waves in the earth. The speed of S waves is about 4.5 km /s and that of P waves is about 8.0 km/s . A seismograph records P and S waves from an earthquake. The first P wave arrives 4.0 min before the first S wave. The epicenter of the earthquake is located at a distance about
View SolutionTwo waves are propagating to the point P along a straight line produced by two sources A and B of simple harmonic and of equal frequency. The amplitude of every wave at P is `a` and the phase of A is ahead by `pi//3` than that of B and the distance AP is greater than BP by `50 cm`. Then the resultant amplitude at the point P will be if the wavelength `1` meter
View SolutionThe superposing waves are represented by the following equations :
`y_(1) 5 sin 2 pi (10 t-0.1 x ), y_(2)=10 sin 2 pi (20t -0.2 x)` Ratio of intensities `(I_("max"))/(I_("min")) ` will be
View SolutionThe correct graph between the frequency n and square root of density `rho` of a wire, keeping its length, radius and tension constant, is
View SolutionTwo identical stringed instruments have frequency 100 Hz . If tension in one of them is increased by 4% and they are sounded together then the number of beats in one second is
View Solutionwhich of the following function corrtly represent the traveling wave equation for finite values of x and t ?
View SolutionA violin string oscillation in its fundamental mode, generates a sound wave with wavelength `lamda`. To generate a sound wave with wavelength `(lamda)/(2)`. By the string still oscillating is its fundamental mode, tension must be changed by the multiple.
View SolutionSinusoidal waves `5.00 cm ` in amplitude are to be transmitted along a string having a linear mass density equal to `4.00xx10^-2kg//m`. If the source can deliver a maximum power of `90W` and the string is under a tension of `100N`, then the highest frequency at which the source can operate is (take `pi^2=10`)
View SolutionWave pulse on a string shown in figure is moving to the right without changing shape. Cosider two particle at positions `x_(1)=1.5 m and x_(2)=2.5 m`. Their transverse velocities at the moment shown in figure are along direction

View SolutionWhat is the percentage change in the tension necessary in a somometer of fixed length to produce a note one octave lower (half of original frequency) than before?
View SolutionA wire having a linear mass density `5.0 xx 10^(-3)` kg/m is stretched between two rigid supports with a tension of 450 N. The wire resonates at a frequency of 420 Hz. The next higher frequency at which the same wire resonates is 480 Hz. Find the length of the wire.
View SolutionA `20 cm` long rubber string fixed at both ends obeys Hook's law. Intially when it is stretched to make its total length of `24 cm`, the lowest frequency resonance is `v_(0)`. It is further stretched to make its total length of `26 cm`. The lowest frequency of resonance will now be :
View SolutionThe equation of a wave is given by (all quantity expressed in S.I units) `y=5sin10pi(t-0.01x)` along the x-axis. The magnitude of phase difference between the points separated by a distance of 10 m along x-axis is
View SolutionWhich of the following travelling wave will produce standing wave , with nodes at `x = 0`, when superimosed on ` y = A sin ( omega t - kx)`
View SolutionEquation of a standing wave is generally expressed as `y=2Asinomegatcoskx`. In the equation quantity `(omega)/(k)` represents
View SolutionThe figure shown at time `t = 0` second, a rectangular and triangular pulse on a uniform wire are approcaching other. The pulse speed is `0.5 cm//s` . The resultant pulse at `t = 2` second is

View Solution[Q. Nos. 3-4] Difference in frequencies between 3rd overtone of closed pipe and 5th haronic of the same pipe is 400 Hz. Futher 3rd hormonic of this closed pipe os equal to 6th hormonic of another open pipe.
Fundamental frequencies of closed pipe and open pipe are
View SolutionIf speed of sound is 330 m/s. The lengths of closed pipe and open pipe are :
View SolutionThe angular frequency is:
View SolutionThe wave speed is :
View SolutionThe rate at which the wave transports energy is :
View SolutionThe equation of resultant wave due to the two waves is `y' (x, t)`
View SolutionOut of the three wave equations `y'(x,t)` and the resultant `y' (x, t)`, which wave would you actually see on the string?
View SolutionA wave pulse is generated in a string that lies along `x-`axis. At the points `A` and `B`, as shown in figure, if `R_(A)` and `R_(B)` are ratio of magnitudes of wave speed to the particle speed, then
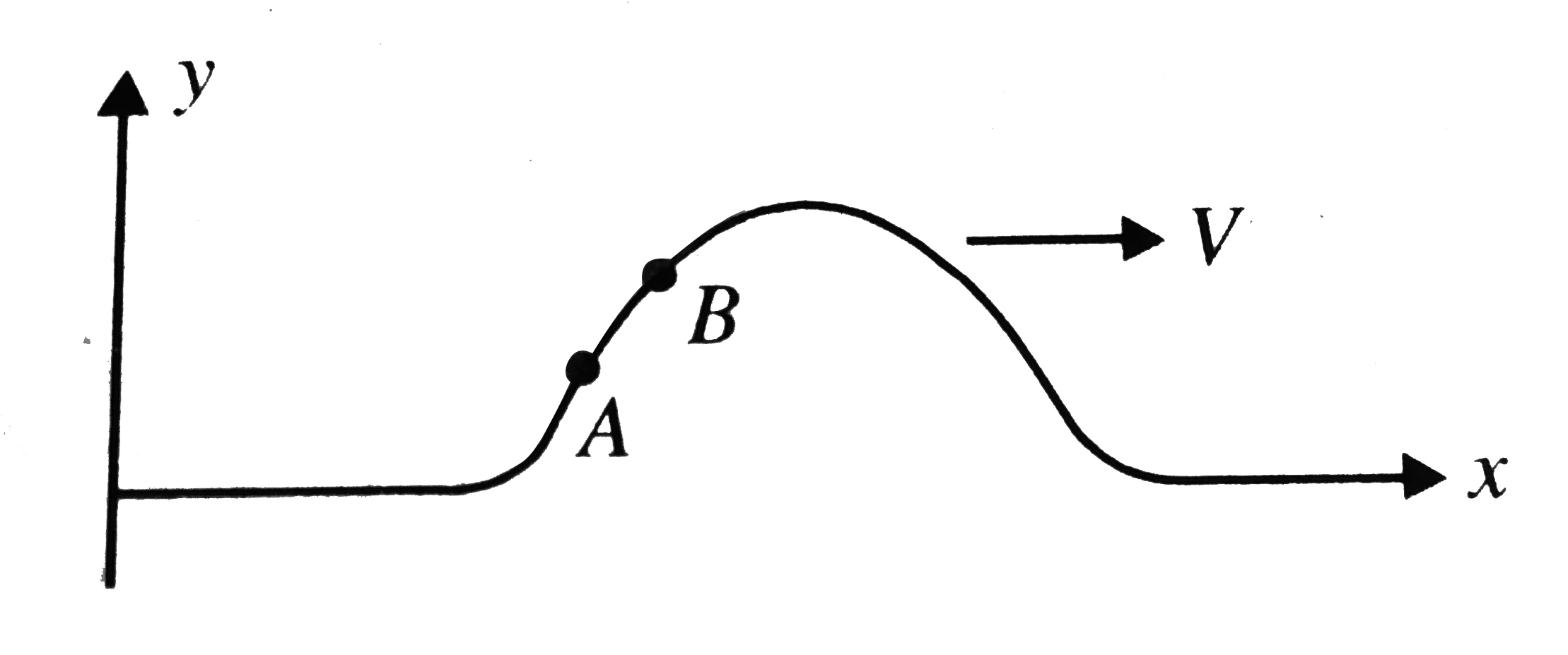
View Solution
When a wave pulse travelling in a string is reflected from rigid wall to which string is tied as shown in figure. For this situation two statements are given below.
(1) The reflected pulse will be in same orientation of incident pulse due to a phase change of `pi` radians
(2) During reflection the wall exert a force on string in upward directon for the above given two statements choose the correct option given below
View SolutionA transverse wave described by equation `y=0.02sin(x+30t)` (where x and t are in metres and seconds, respectively) is travelling along a wire of area of cross-section `1mm^2` and density `8000kg//m^(2)`. What is the tension in the string?
View SolutionTwo vibrating strings of same material stretched under same tension and vibrating with same frequency in the same overtone have radii 2r and r. Then the ratio of their lengths is:
View SolutionA wave moving with constant speed on a uniform string passes the point `x=0` with amplitude `A_0`, angular frequency `omega_0` and average rate of energy transfer `P_0`. As the wave travels down the string it gradually loses energy and at the point `x=l`, the average rate of energy transfer becomes`P_0`/2. At the point `x=l`. Angular frequency and amplitude are respectively:
View SolutionA standing wave pattern is formed on a string.One of the waves is given by equation `y_(1)=a cos(omega t-kx+(pi)/(3))` ,then the equation of the other wave such that `x=0` a node is formed is-
View SolutionThe `(x, y)` co-ordinates of the corners of a square plate are `(0, 0)`, `(L, L)` and `(0, L)`. The edges of the plate are clamped and transverse standing waves are set up in it. If `u(x, y)` denotes the displacement of the plate at the point `(x, y)` at some instant of time, the possible expression `(s)` for `u` is (are) `(a = positive constant)`
View SolutionThe paritcle displacement (in cm) in a stationary wave is given by `y(x,t)=2sin(0.1pix)cos(100pit)`. The distance between a node and the next antinode is
View SolutionA wire of length l having tension T and radius `r` vibrates with fundamental frequency `f`. Another wire of the same metal with length `2l` having tension `2T` and radius `2r` will vibrate with fundamental frequency :
View SolutionA transverse wave is propagating along `+x` direction. At `t=2` sec the particle at `x=4`m is at `y=2` mm. With the passage of time its `y` coordinate increases and reaches to a maximum of 4 mm. The wave equation is (using `omega` and `k` with their usual meanings)
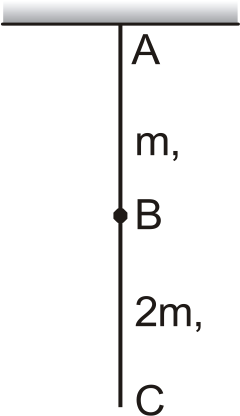
View SolutionIn the figure shown strings AB and BC have masses m and 2m respectively. Both are of same length l.Mass of each string is uniformly distributed on its length. The string is suspended vertically from the ceiling of a room.A small jerk wave pulse is given at the end 'C'.It goes up to upper end 'A' in time 't' .If the value of t is given by `a sqrt(l/g)+b sqrt(l/g)(sqrtc-sqrtd)` then a+b+c+d is
View SolutionA `75 cm` string fixed at both ends produces resonant frequencies `384 Hz and 288 Hz` without there being any other resonant frequency between these two . Wave speed for the string is
View SolutionA string of length 'L' is fixed at both ends . It is vibrating in its ` 3rd` overtone with maximum amplitude 'a'. The amplitude at a distance `L//3` from one end is
View SolutionA `40 cm` long wire having a mass `3.2 g` and area of cross - section ` 1 mm^(2)` is stretched between the support `40 .05 cm` apart. In its fundamental mode , it vibrates with a frequency `1000//64 Hz`. Find the young's modulus of the wire.
View SolutionA string of length 1.5 m with its two ends clamped is vibrating in fundamental mode. Amplitude at the centre of the string is 4 mm. Minimum distance between the two points having amplitude 2 mm is:
View SolutionA string is fixed at both ends. The tension in the string and density of the string are accurately known but the length and the radius of cross section of the string are known with some errorl If maximum errors made in the measurements of length and radius are `1%` and `0.5%` respectively them what is the maximum possible percentage error in the calculation of fundamental frequencyof the that string ?
View SolutionA string of length l' fixed at both ends vibrates in resonance with a tuning fork of frequency 'f' at two successive values of tension `T_(1)` and `T_(2)` inthe string. Findthe specificmass (mass per unit length) ofthe string:
View SolutionA block of mass 2m is hanging at the lower and of a ropeof mass m and length the l, the other end being fixed to the ceililng. A pulse of wavelength `lamda_(0)` is produced at the lower of the rope.
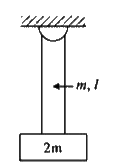
The wavelength of the pulse when it reaches the other end of the rope is :
View SolutionA block of mass 2m is hanging at the lower and of a ropeof mass m and length the l, the other end being fixed to the ceililng. A pulse of wavelength `lamda_(0)` is produced at the lower of the rope.
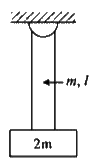
The speed of the pulseat the mid point of rope is:
View SolutionA block of mass 2m is hanging at the lower and of a ropeof mass m and length the l, the other end being fixed to the ceililng. A pulse of wavelength `lamda_(0)` is produced at the lower of the rope.
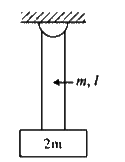
The time taken by the pulse to reach the other end of the rope is:
View SolutionA standing wave exists in string of length 150 cm fixed at both ends. The displacement amplitude of a point at a distance of 10 cm from one of ends if `5sqrt(3)mm`. The distance between two nearest points, within the same loop having the same displacement amplitude of `5sqrt(3)` is 10 nm.
The maximum displacement amplitude of the particle in the string is,:
View SolutionA standing wave exists in string of length 150 cm fixed at both ends. The displacement amplitude of a point at a distance of 10 cm from one of ends if `5sqrt(3)mm`. The distance between two nearest points, within the same loop having the same displacement amplitude of `5sqrt(3)` is 10 nm.
The maximum displacement amplitude of the particle in the string is,:
View SolutionA standing wave exists in string of length 150 cm fixed at both ends. The displacement amplitude of a point at a distance of 10 cm from one of ends if `5sqrt(3)mm`. The distance between two nearest points, within the same loop having the same displacement amplitude of `5sqrt(3)` is 10 nm.
The maximum displacement amplitude of the particle in the string is,:
View SolutionA transverse sinusoidal wave is generted at one end of long, horizontal string by a bar that moves up and down through a distance of `1.00 cm`. The motion is continuous and is repreated regularly `120` times per second. The string has linear density `90 gm//m` and is kept under a tension of `900 N`. Find :
What is the maximum power (in watt) transferred along the string.
View SolutionA transverse sinusoidal wave is generted at one end of long, horizontal string by a bar that moves up and down through a distance of `1.00 cm`. The motion is continuous and is repreated regularly `120` times per second. The string has linear density `90 gm//m` and is kept under a tension of `900 N`. Find :
What is the maximum power (in watt) transferred along the string.
View SolutionA transverse sinusoidal wave is generated at one end of a long horizontal string by a bar is continuous and is repeated regularly 120 times per second. The string has linear density of 117g/m. the other end of the string is attached to a mass 4.68kg. the string passes over a smooth pulley and the mass attached to the other end of the string hangs freely under gravity.
The maximum power transferred along the string is:
View SolutionThe wave-function for a certain standing wave on a string fixed at both ends is `y(x,t) = 0.5 sin (0.025pix) cos500t` where `x` and `y` are in centimeters and `t` is seconds. The shortest possible length of the string is :
View SolutionA loop of a string of mass per unit length `mu` and radius R is rotated about an axis passing through centre perpendicular to the plane with an angular velocityco. A small disturbance is created in the loop having the same sense of rotation. The linear speed of the disturbance for a stationary observer is :
View SolutionGraph shows three waves that are separately sent along a string that is stretched under a certain tension along x-axis. If `omega_(1),omega_(2) and omega_(3)` are their angular frequencies, respectively, then:

View SolutionThe same progressive wave is represented by two graphs `I` and `II`. Graph `I` shows how the displacement `'y'` varies with the distance `x` along the wave at a given time. Graph `I` shows how `y` varies with time `t` at a given point on the wave. The ratio of measurements `AB` to `CD`, marked on the curves, represents :
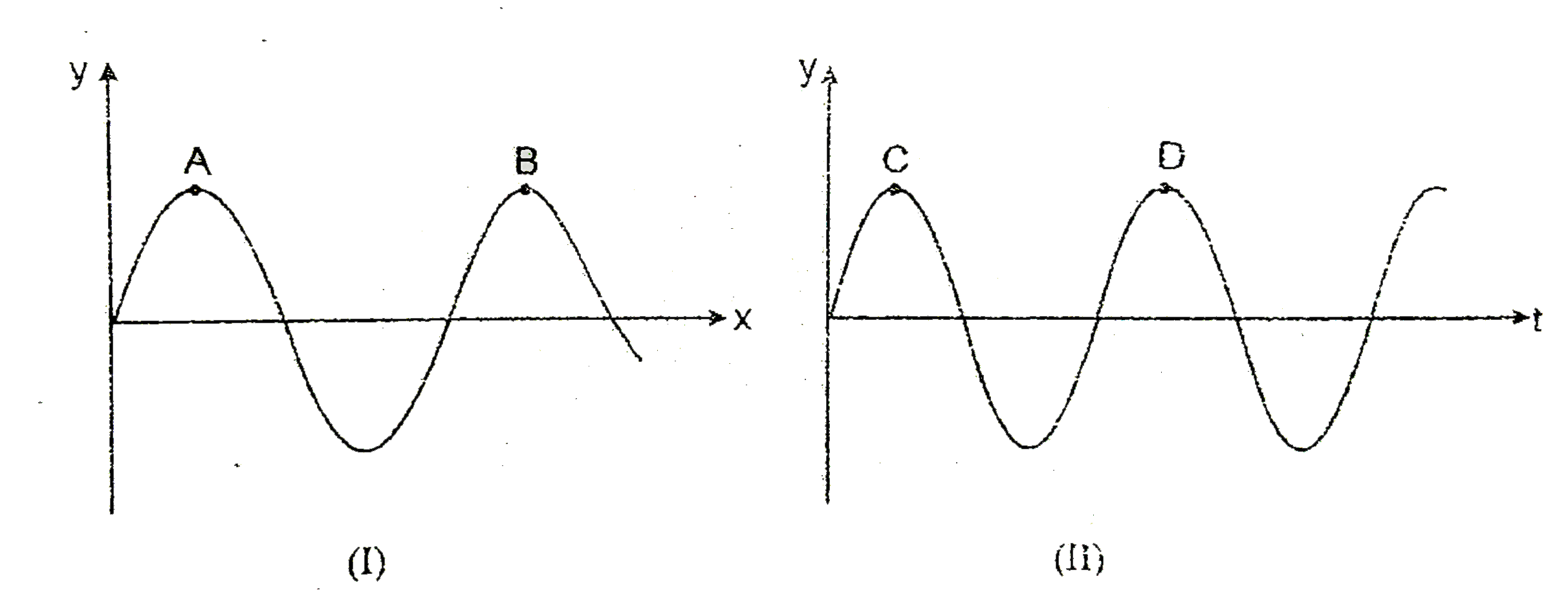
View SolutionA transverse periodic wave on a string with a linear mass density of `0.200 kg//m` is described by the following equation
`y = 0.05 sin(420t - 21.0 x)`
where `x` and `y` are in meters and `t` is in seconds.
The tension in the string is equal to :
View SolutionA certain transverse sinusoidal wave of wavelength 20 cm is moving in the positive x direction. The transverse velocity of the particle at x=0 as a function of time is shown. The amplitude of the motion is:

View Solutiontwo particle of medium disturbed by the wave propagation are at `x_(1)=0 and x_(2)=1 cm`. The respective displacement (in cm) of the particles can be given by the equation:
`y_(1)=2 sin 3pi t, y_(2) sin (3pi t-pi//8)` the wave velocity is
View SolutionA travelling wave `y=A sin (kx- omega t +theta )` passes from a heavier string to a lighter string. The reflected wave has amplitude `0.5A` . The junction of the strings is at `x=0`. The equation fo the refelcted wave is `:`
View SolutionIn the above question, the displacement of particle at t = 1 sec and x = 4 cm is:
View SolutionSpacing between two successive nodes in a standing wave on a string is `x`. If frequency of the standing wave is kept unchanged but tension in the string is doubled, then new sapcing between successive nodes will become:
View SolutionTwo small boats are `10m` apart on a lake. Each pops up and down with a period of 4.0 seconds due to wave motion on the surface of water. When one boat is at its highest point, the other boat is its lowest point. Both boats are always within a single cycle of the waves. The speed of the waves is:
View Solution
Numerical MCQs Single Options Correct questions and complete solutions for chapter WAVES of GK PUBLICATIONS PHYSICS (HINGLISH) of Class 12
All Exercises from PHYSICS GALAXY Class 12 PHYSICS WAVES
- Advance MCQs with One or More Options Correct
- Conceptual MCQs Single Option Correct
- Discussion Question
- Illustrative
- Numerical MCQs Single Options Correct
- Practice Exercise 6.1
- Practice Exercise 6.2
- Practice Exercise 6.3
- Practice Exercise 6.4
- Practice Exercise 6.5
- Practice Exercise 6.6
- Practice Exercise 6.7
- Practice Exercise 6.8
- Unsolved Numerical Problems for Preparation of NSE, INPhO & IPhO