Complete Solutions to LONG ANSWER QUESTIONS of chapter ELECTROSTATICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTROSTATICS |
| PRADEEP | LONG ANSWER QUESTIONS |
| Number Of Questions | 8 |
| Academic Year | 2023-24 |
Derive an expression for electric field intensity at a point due to point charge.
View Solution`(i)` If two similar large plates, each of area A having surface charge densities `+sigma` and `-sigma` are separated by a distance `d` in air,find the expression for
`(a)` field at points between the two plates and on outer side of the plates. Specify the direction of the field in each case.
`(b)` the potential difference between the plates.
`(c)` the capacitance of the capacitor so formed.
`(ii)` Two metallic spheres of radii `R` and `2R` are charged so that both of these have same surface charge density `sigma`. If they are connected to each other with a conducting wire, in which direction will the charge flow and why ?
View SolutionIn 1959, Lytteton and Bondi suggest that the expansion of the Universe could be explained fi matter carried a net charge. Suppose that the Universe is made up of hydrogen atoms with a number density N, which is mainted a constant. Let the charge on the proton be , `e_(p) = -(1+q)` e where e si the electronic charge.
(a) Find the critical value of y such that expansion may start.
(b) Show that the velocity of expansion is propertional to the distance from the center.
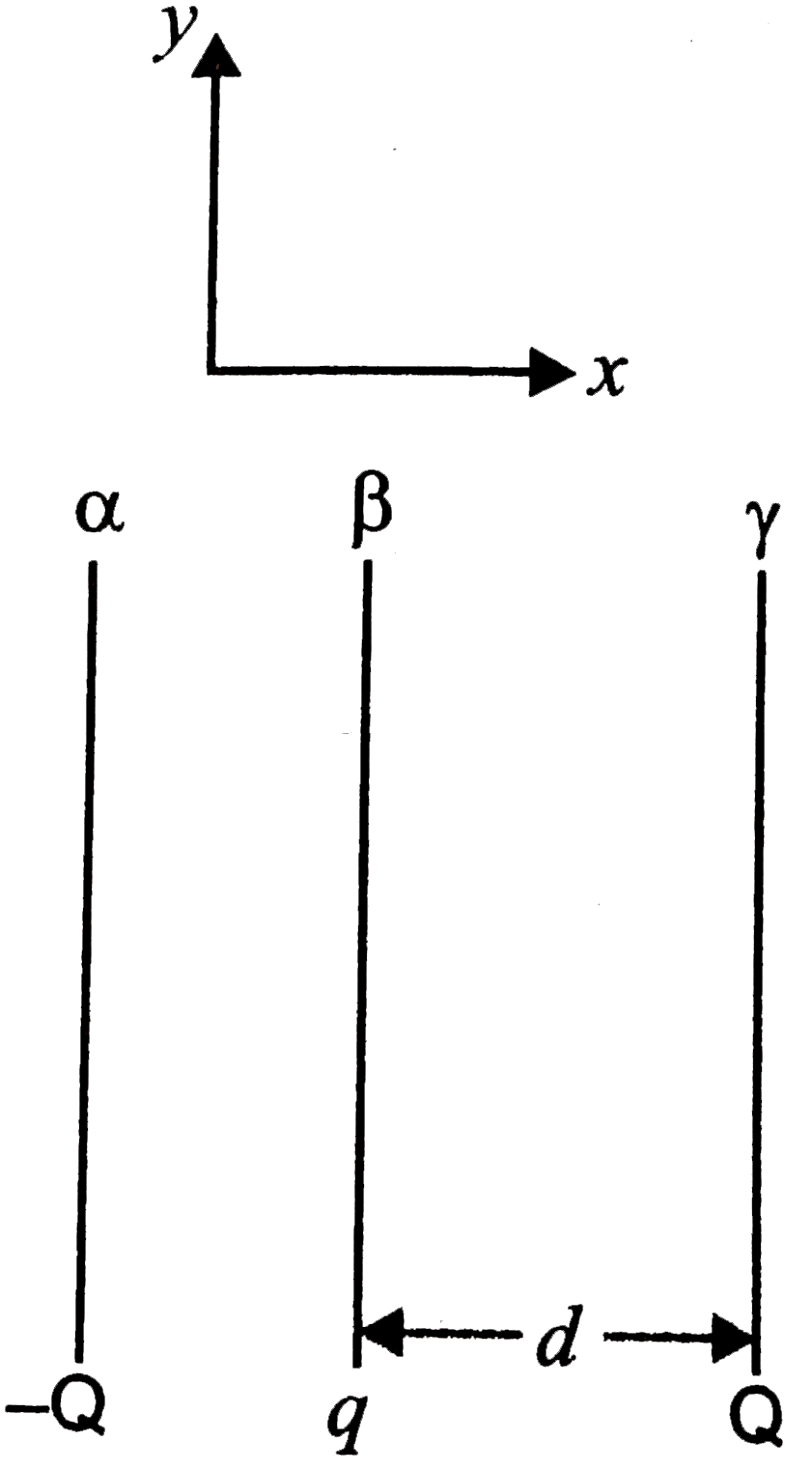
View SolutionTwo fixed, identical conducting plates `(alpha and beta)`, each of surface area S are charged to `-Q and q`, respectively, where `Q gt q gt 0`. A third indentical plate `(gamma)`, free to move is located on the other side of the plate with charge q at a distance d, fig. The third plate is released and collidies with the plate `beta`. Assume the collsion is electric and the time of collision is sufficient to redistribute charge amongst `beta and gamma`.
(a) Find the electric field acting on the plate `gamma` before collision.
(b) Find the charge on `beta and gamma` after the collision.
(c) Find the velocity of the plate `gamma` after the collision and at a distance d from the plate `beta`.
View SolutionThree is another useful system of units, besides the SI/mksA system, called the cgs (centimeter-gram -second) system, Coulumb's law is given by `F = (Qq)/(r^(2)) hat(r )` where the distance r is measured in cm `(=10^(-2)m)`, F in dynes `(=10^(-5) N)` and the charges in electrostatic units (es units), where 1 es unit of charge `=(1)/([3]) xx 10^(-9) C`
The number `[3]` actually aries from the speed of light in vacumm which is now taken to be exactly given by `c = 2.99792458xx10^(8) m//s`. An approximate value of c then is `c = [3] xx10^(8) m//s`.
(i) Show that the coulomb law in cgs units yields 1 esu of charge `= 1 (dyn e)^(1//2)cm`. Obtain the dimensious of units of charge in terms of mass M, length L and time T. Show that it is given in terms of fractional powers of M and L.
(ii) Write 1 esu of charge `= xC`, where x is a dimenionless number. Show that this gives
`(1)/(4pi in_(0)) = (10^(-9))/(x^(2)) (N.m^(2))/(C^(2)) With x = (1)/([3]) xx10^(-9)`, we have
`(1)/(4pi in_(0)) = [3]^(2) xx10^(9) (Nm^(2))/(C^(2)) or (1)/(4pi in_(0)) = (2.99792458)^(2) xx 10^(9) (Nm^(2))/(C^(2))` (exactly).
View SolutionFind the equatio of the equipotentials for an infinite cylinder of radius `r_(0)` carrying charge of linear density `lamda`.
View SolutionTwo charges `q_(1) and q_(2)` are placed at (0,0,d) and (0,0,-d) respectively. Find locus of points where the potential is zero.
View SolutionTwo charges -q each are separated by dsitance 2d. A third charge +q is kept at mid-point O. find potential energy of +q as function of small distance x from 0 due to -q charges. Sketch PE Vs/x and convince yourself that the charge at 0 is in an unstable equilibrium.
View Solution
LONG ANSWER QUESTIONS questions and complete solutions for chapter ELECTROSTATICS of PRADEEP PHYSICS (HINGLISH) of Class 12
All Exercises from PRADEEP Class 12 PHYSICS ELECTROSTATICS
- ADDITIONAL QUESTIONS
- ADVANCED PROBLEMS FOR COMPETITIONS
- ASSERTION-REASON TYPE QUESTIONS
- COMPREHENSION
- CONCEPTUAL PROBLEMS
- CURIOSITY QUESTIONS
- Exercise
- FILL IN THE BLANKS
- LONG ANSWER QUESTIONS
- MULTIPLE CHOICE QUESTIONS
- NCERT QUESTIONS
- PROBLEMS FOR PRACTICE
- SHORT ANSWER QUESTIONS
- TYPICAL EXAMPLES
- VALUE BASED QUESTIONS
- VERY SHORT ANSWER QUESTIONS