Two fixed, identical conducting plates (αandβ), each of surface area S are charged to −Qandq, respectively, where Q>q>0. A third indentical plate (γ), free to move is located on the other side of the plate with charge q at a distance d, fig. The third plate is released and collidies with the plate β. Assume the collsion is electric and the time of collision is sufficient to redistribute charge amongst βandγ.
(a) Find the electric field acting on the plate γ before collision.
(b) Find the charge on βandγ after the collision.
(c) Find the velocity of the plate γ after the collision and at a distance d from the plate β.
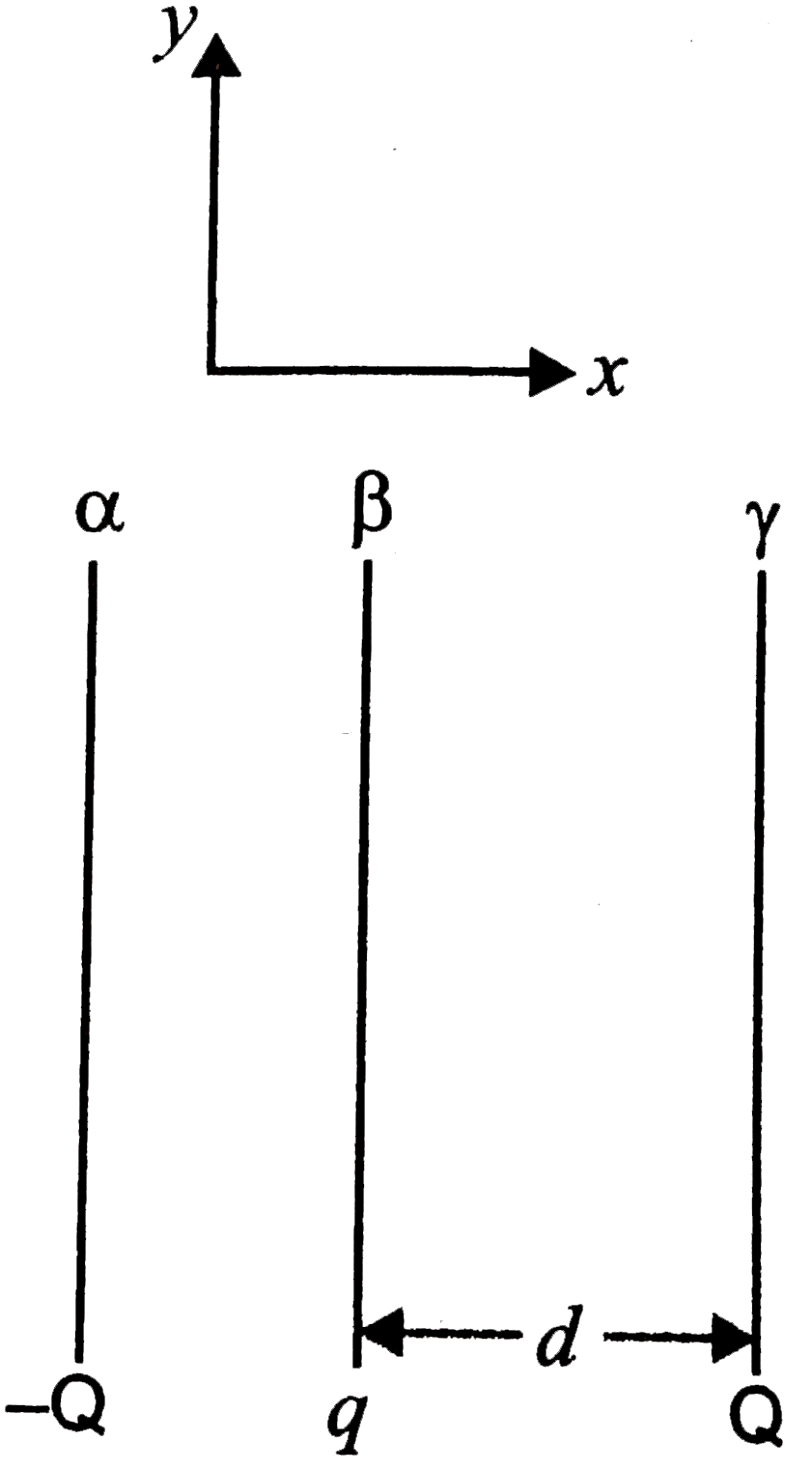
The given set up is shown in Fig.
(a) The electric field at plate γ due to plate α is
E1=−QS(2∈0) , to the left
The electric field at plate γ to plate β is
E2=qS(2∈0) , to the right.
Hence, the net electric field at plate lamma before collision is
E=E1+E2=q−QS(2∈0) , to the left if Q>q
(b) During collision, plates βandγ are together. Their potentials become same. Suppose charge on plane βisq1 and charge on plate γisq2. At any point 0, inbetween the two plates, Fig, the electric field must be zero.
Electric field at 0 due to plate α=(−)QS(2∈0) , to the left
Electric field at 0 due to plate β=q1S(2∈0) , to the right
Electric field at 0 due to plate γ=q2S(2∈0) , to the left
As the electric field at 0 is zero, therefore , Q+q2S(2∈0)=q1S(2∈0)
∴Q+q2=q1orQ=q1−q2 ...(i)
As there is no loss of charge on collision, Q+q=q1+q2 ...(ii)
On solving (i) and (ii),we get q1=(Q+q/2) = charge on plate γ.
(c) After collision,at a distance d from plate β, let the velocity of plate γ be v.
After the collision, electric field at plate γ is E2=−Q2∈0S+(Q+q/2)2∈0S=q/22∈0S to the right.
Just before collision, electric field at plate γ is E1=Q−q2∈0S
If F1 is force on plate γ before collision, then F1=E1Q=(Q−q)Q2∈0S
Similarly, force F2 on plate γ after collision, F2=E2q2=(q/2)22∈0S
Total work done by the electric field in round trip movement of plate γ
W=(F1+F2)d=[(Q−q)Q+(q/2)2]d2∈0S=(Q−q/2)2d2∈0S
If m is mass of plate γ, the KE gained by plate γ=12mv2
According to work energy principle, 12mv2=W=(Q−q/2)2d2∈0S
v=(Q−q/2)(dm∈0s)1/2

Topper's Solved these Questions
- ELECTROSTATICSBOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - VALUE BASED QUESTIONS
7 Videos
- ELECTROSTATICSBOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - Exercise
414 Videos
- ELECTROSTATICSBOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL QUESTIONS
2 Videos
- ELECTRONIC DEVICESBOOK - PRADEEPCHAPTER - ELECTRONIC DEVICESEXERCISE - Fill in the Blanks
1 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Competition Focus (Multiple Choice Questions)
2 Videos
Similar Questions
Two fixed, identical conducting plates (αandβ), each of surface area S are charged to -Q and q, respectively, where Q > q > 0. A third identical plate (γ), free to move is located on the other side of the plate with charge Q at a distance d (figure). The third plate is released and collides with the plate β. Assume the collision is elastic and the time of collision is sufficient to redistribute charge amongst βandγ.
(a) Find the electric field acting on the plate γ before collision.
(b) Find the charges on βandγ after the collision.
(c) Find the velocity of the plate γ after the collision and at a distance d from the plate β.
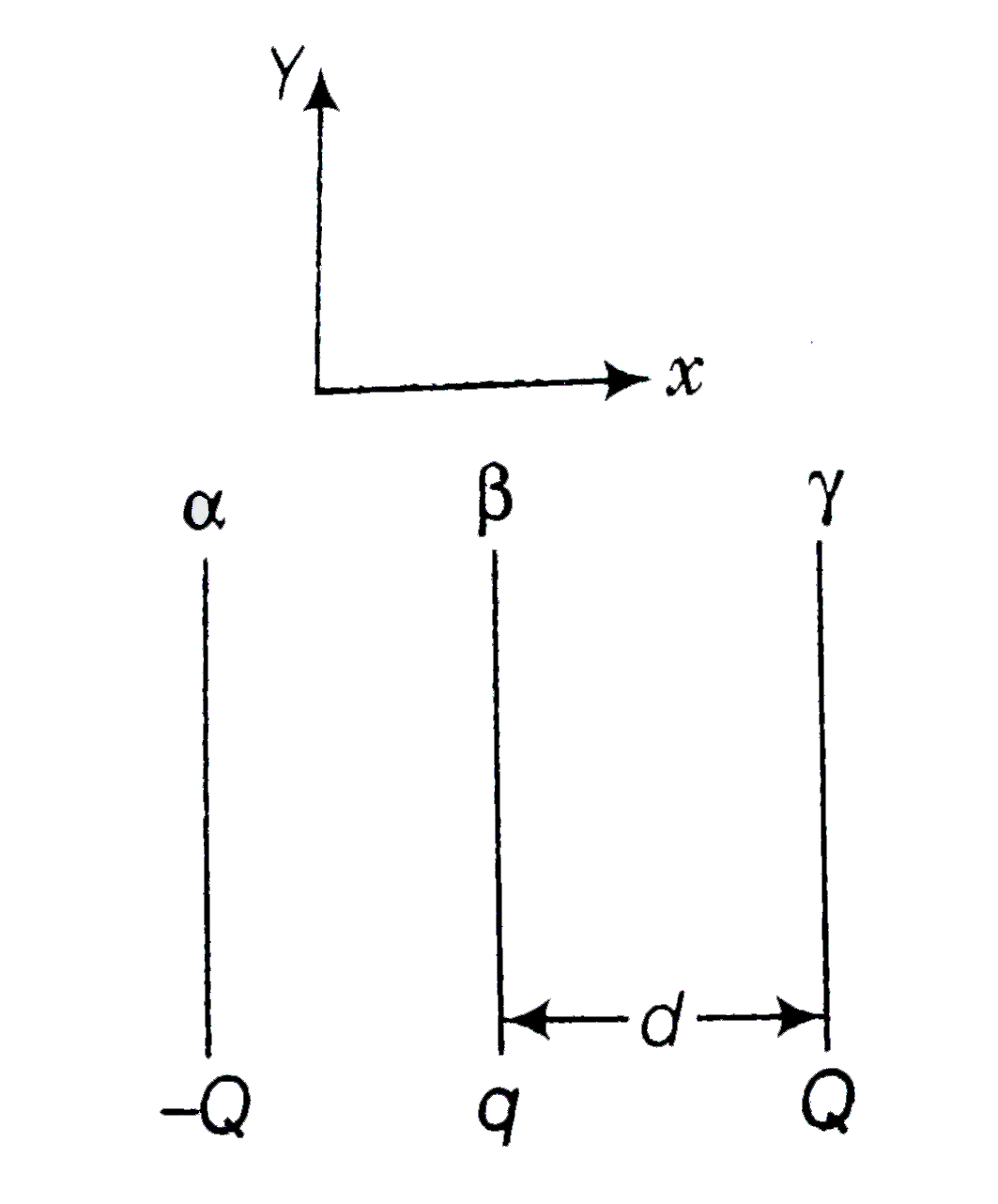
View SolutionForce between two conducting large plates , with charges Q and Q2 as shown in the figure, is (Area of each face of plate =A)
_PHY_E01_022_Q01.png)
View Solution
Knowledge Check
Five identical plates are connected across a battery as follows : If the charge on plate 1 be +q, then the charges on the plates 2,3,4 and 5 are
 A−q,+q,+qB−2q,+2q,−2q,+qC−q,+2q,−2q,+qDNone of above
A−q,+q,+qB−2q,+2q,−2q,+qC−q,+2q,−2q,+qDNone of above
Force between two conducting large plates , with charges Q and Q2 as shown in the figure, is (Area of each face of plate =A)
_PHY_E01_022_Q01.png)
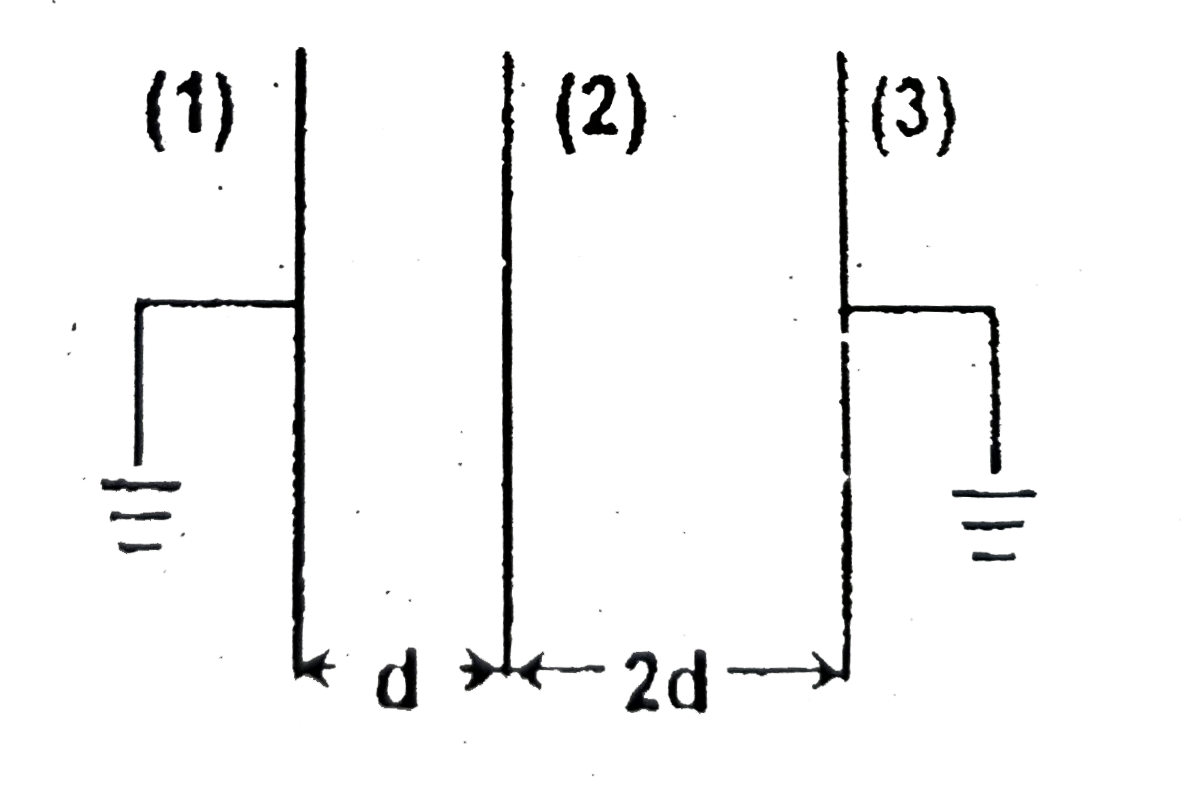
View SolutionTwo identical metal plates each having surface area A, having charges q1andq2, are placed facing each other at a separation d. Find the charge appearing on
surface (1),(2),(3), and (4). Assume the size of the plate is much larger than the separation between the plates.
View SolutionTwo identical metal plates each having surface area A, having charges q1andq2, are placed facing each other at a separation d. Find the charge appearing on
surface (1),(2),(3), and (4). Assume the size of the plate is much larger than the separation between the plates.
View SolutionTwo large conducting plates of a parallel plate capacitor are given charges Q and 3Q respectively. If the electric field in the region between the plates is E0 , then the force of interaction between the plates is

View SolutionTwo large conducting plates of a parallel plate capacitor are given charges Q and 3Q respectively. If the electric field in the region between the plates is E0 , then the force of interaction between the plates is

View SolutionThree identical plates of area A are arranged as shown. A charge +Q is given to plate (2). Then,
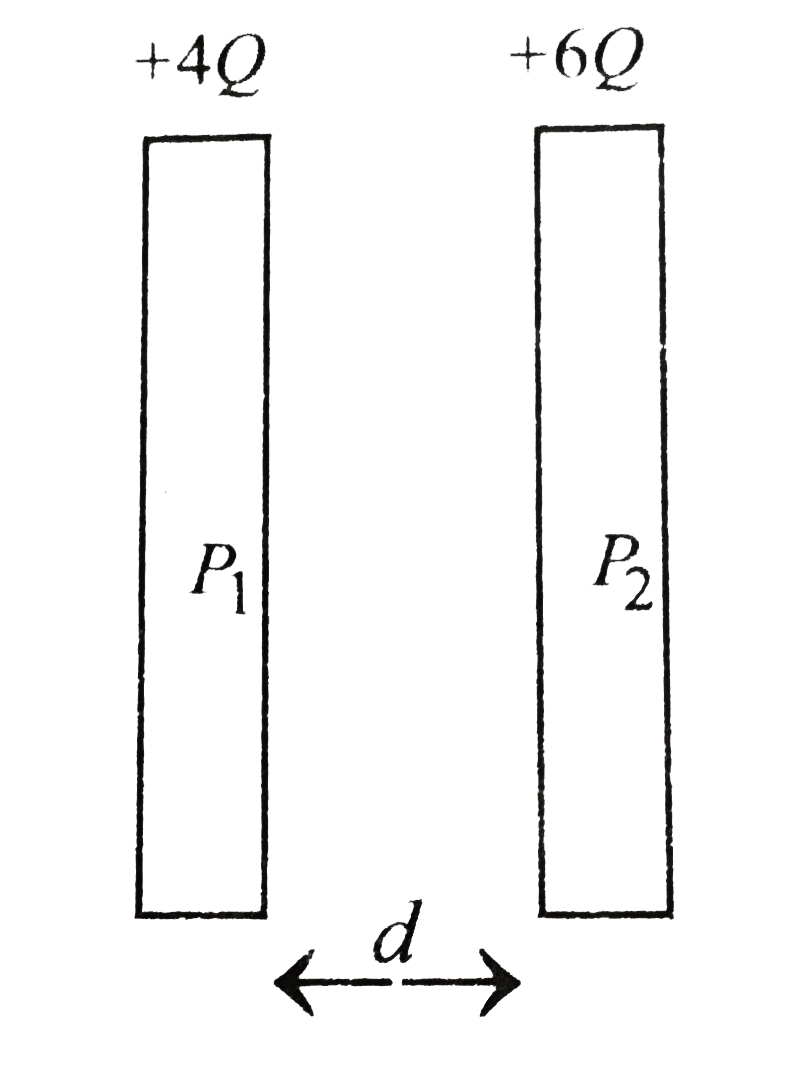
View SolutionTwo identical conducting very large plates P1andP2 having charges +4Qand+6Q are placed very closed to each other at separation d. The plate area of either face of the plate is A. The potential difference between plates P1andP2 is
View Solution
