Complete Solutions to Solved Examples of chapter MAGNETIC EFFECT OF CURRENT AND MAGNETISM of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MAGNETIC EFFECT OF CURRENT AND MAGNETISM |
| PRADEEP | Solved Examples |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
An `alpha`-particle of mass `6.65xx10^-27kg` is travelling at right angles to a magnetic field with a speed of `6xx10^5ms^-1`. The strength of the magnetic field is `0.2T`. Calculate the force on the `alpha`-particle and its acceleration.
View SolutionAn element, `Deltavect=Deltaxhati` is placed at the origin as shown in figure and carries a current 5A. Find out the magnetic field at point P on the z-axis at a distance of `2-0m` due to the element `Deltax=1cm`. Give also, the direction of the magnetic field produced.

View SolutionAn infinitely long straight conductor carries a current of `100A`. At what distance from the conductor is the magnetic field caused by the current equal to `0.5xx10^-4T`?
View SolutionFind an expression for the magnetic field induction at the centre of a coil bent in the form of a square of side `2a`, carrying current I, figure
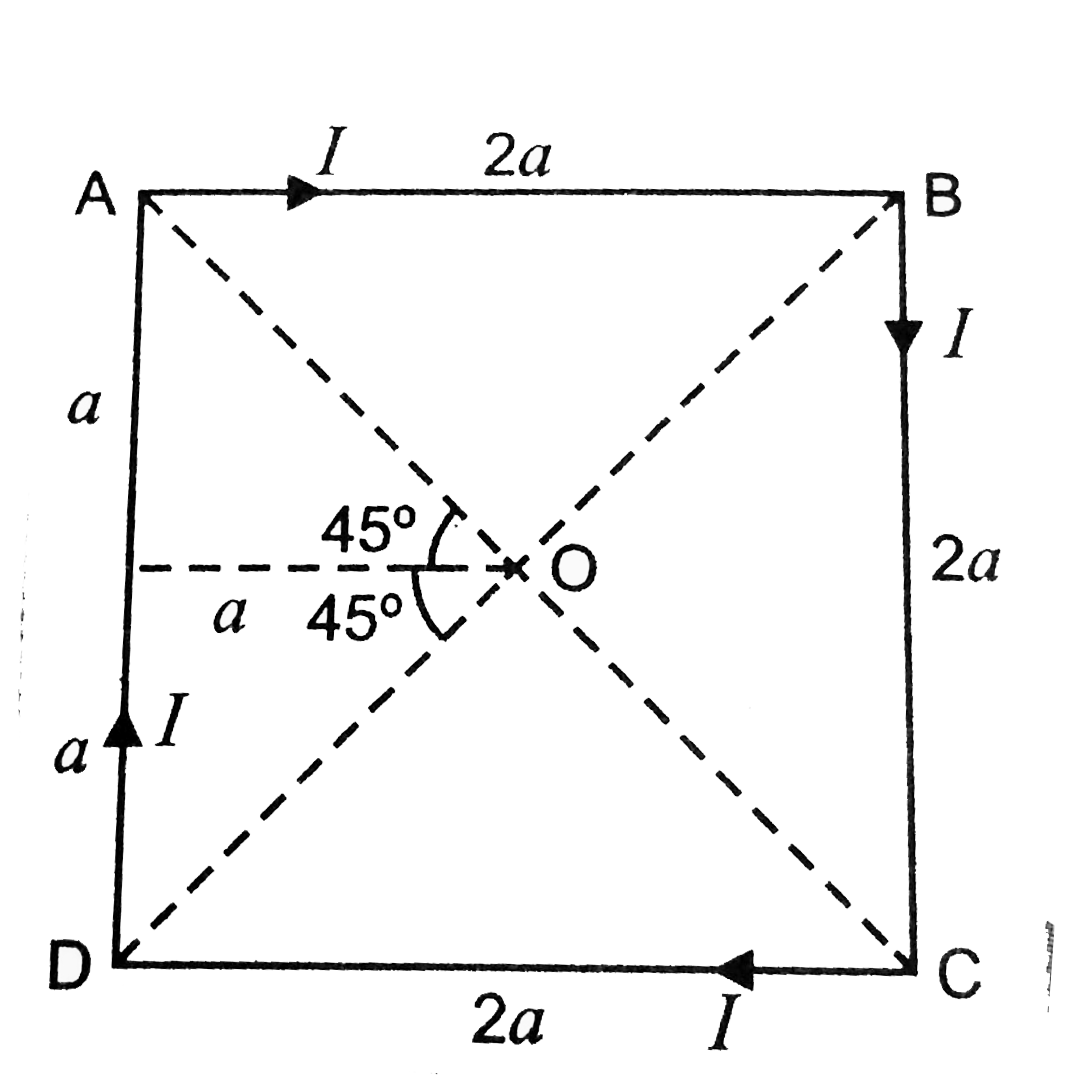
View SolutionIn hydrozen atom, the electron is making `6.6xx10^(15)` revolution per second in a circular path of radius `0.53A^@`. What is the magnetic induction produced at the centre of the orbit?
View SolutionA circular current carrying coil has a radius R. The distance from the centre of the coil on the axis where the magnetic induction will be `(1//8)^(th)` of its value at the centre of the coil is,
View SolutionThere are two parallel current carrying wires X and Y as shown in figure. Find the magnitude and direction of the magnetic field at points, P, Q and R.
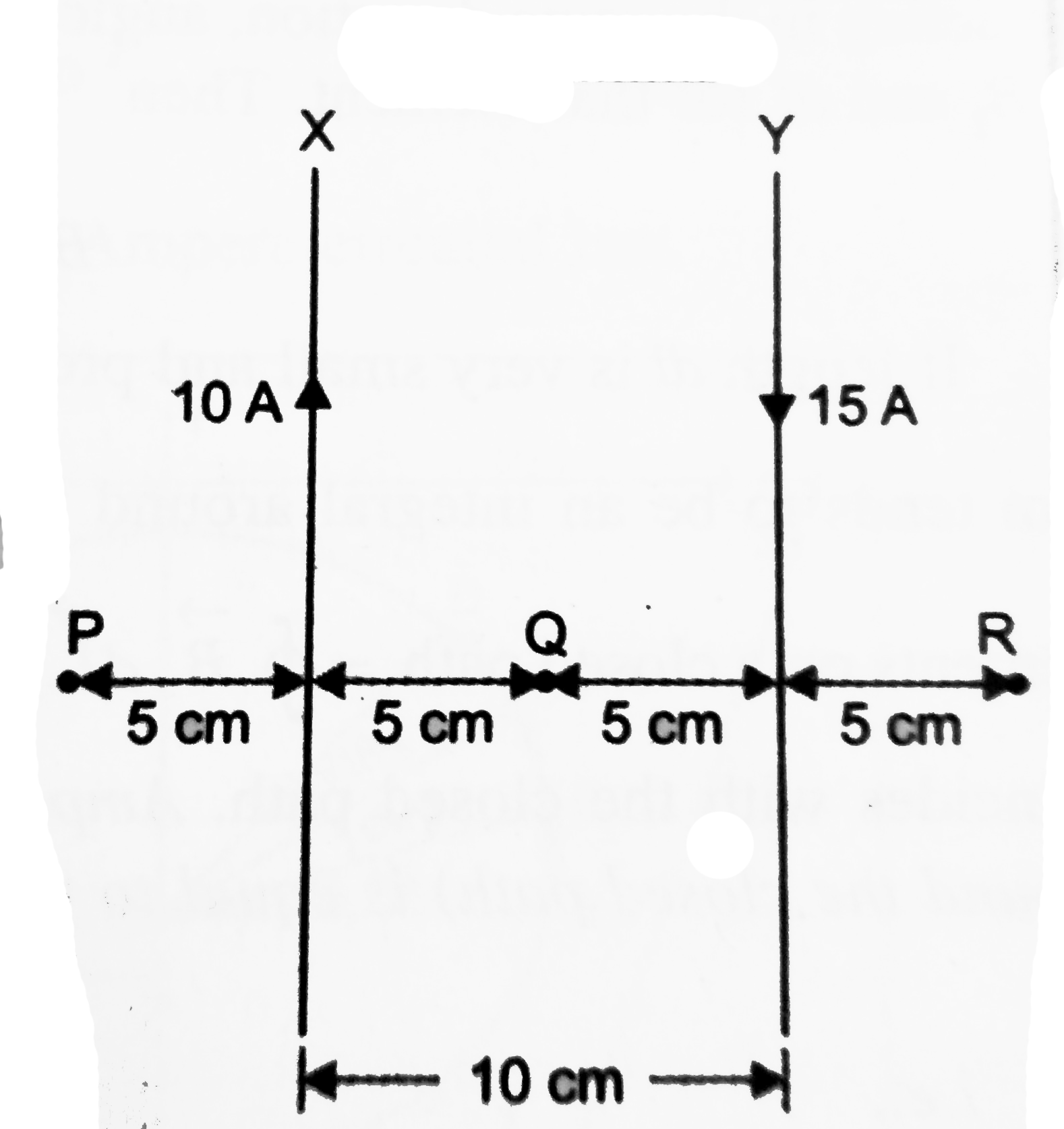
View SolutionA long straight solid metal rod of radius `4cm` carries a current `2A`, uniformly distributed over its circular cross-section. Find the magnetic field induction at a distance `3cm` from the axis of the wire.
View SolutionA solenoid `50cm` long has 4 layers of windings of `350` turns each. The radius of the lowest layer is `1*4cm`. If the current carried is `6*0A`, estimate the magnitude of magnetic flux density (i) near the centre of the solenoid on its axis, (ii) near the ends on its axis, (iii) outside the solenoid near its centre.
View SolutionA coil wrapped around a toroid has inner radius of `10*0cm` and outer radius of `12*0cm`. If the wire wrapped makes `1100` turns and carries a current of `5A`, find the magnetic field (a) inside the core of the toroid (b) outside the toroid at a distance `10cm` from the other surface of toroid.
View SolutionA current of `5A` is flowing from south to north in a straight wire. Find the magnetic field due to a `1cm` piece of wire at a point `1m` north east from the piece of wire.
View SolutionAn element `dvecl=dxhati` (where `dx=1cm`) is placed at the origin and carries a large current `i=10A`. What is the magnetic field on the Y-axis at a distance of `0.5m`?
View SolutionA current element `3dl` is at `(0,0,0)` along y-axis. If `dl=1cm`, find the magnetic field at a distance `20cm` on the x-axis.
View SolutionA straight wire carries a current of `6A` from south to north direction. What is the magnetic field due to `1cm` piece of wire at a point `50cm`, `30^@` east of north?
View SolutionTwo semi infinitely long straight current carrying conductors are held in the form as shown in figure. One common end of them is at the origin. If both the conductors carry same current I, find the value of the magnetic field induction at a point (a, b).
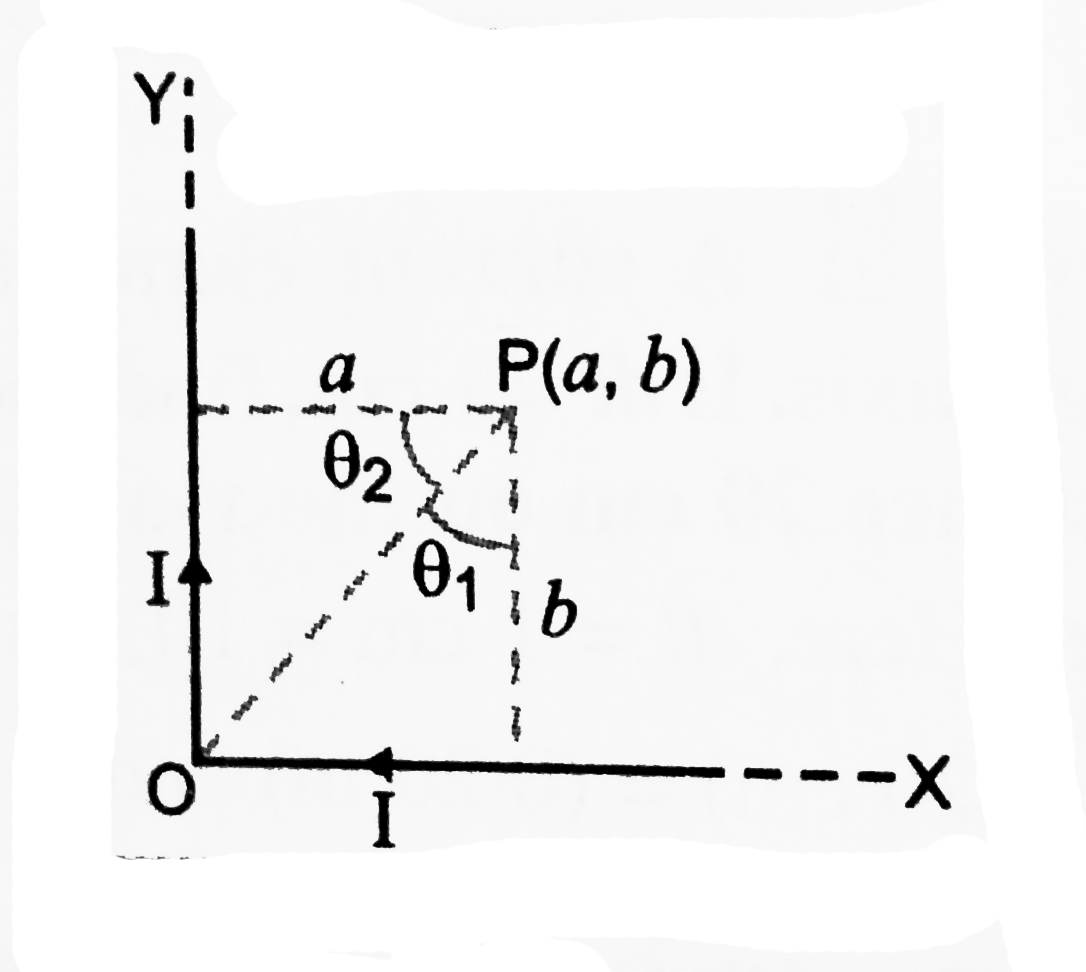
View SolutionSame current i is flowing in the three infinitely long wires along positive x-,y- and z-directions. The magnetic filed at a point (0,0,-a) would be
View SolutionA long straight wire carrying a current of `20A` is placed in an external uniform magnetic field of `3xx10^-4T` parallel to the current. Find the magnitude of resultant field at a point `2*0cm` away from the wire.
View SolutionTwo parallel wires C and D placed perpendicular to the plane of paper at a separation of `r(=8cm)`, carry electric currents `I_1=6A` and `I_2=3A` in opposite directions as shown in figure. Find the point on the line CD where the resultant magnetic field is zero.
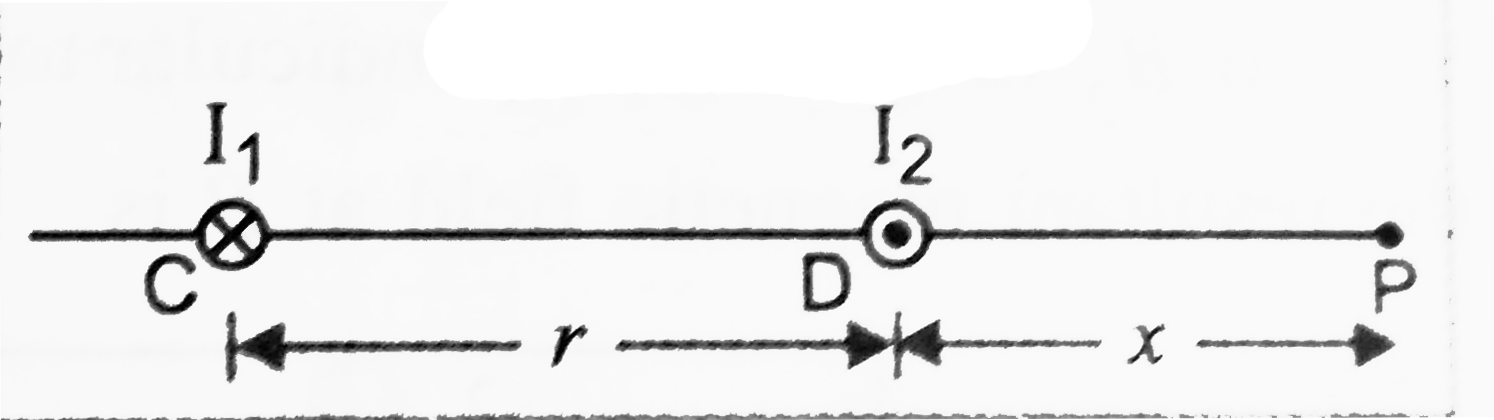
View SolutionThere are two parallel current carrying wires X and Y as shown in figure. Find the distance of a point from wire X, where the resultant magnetic field is zero.
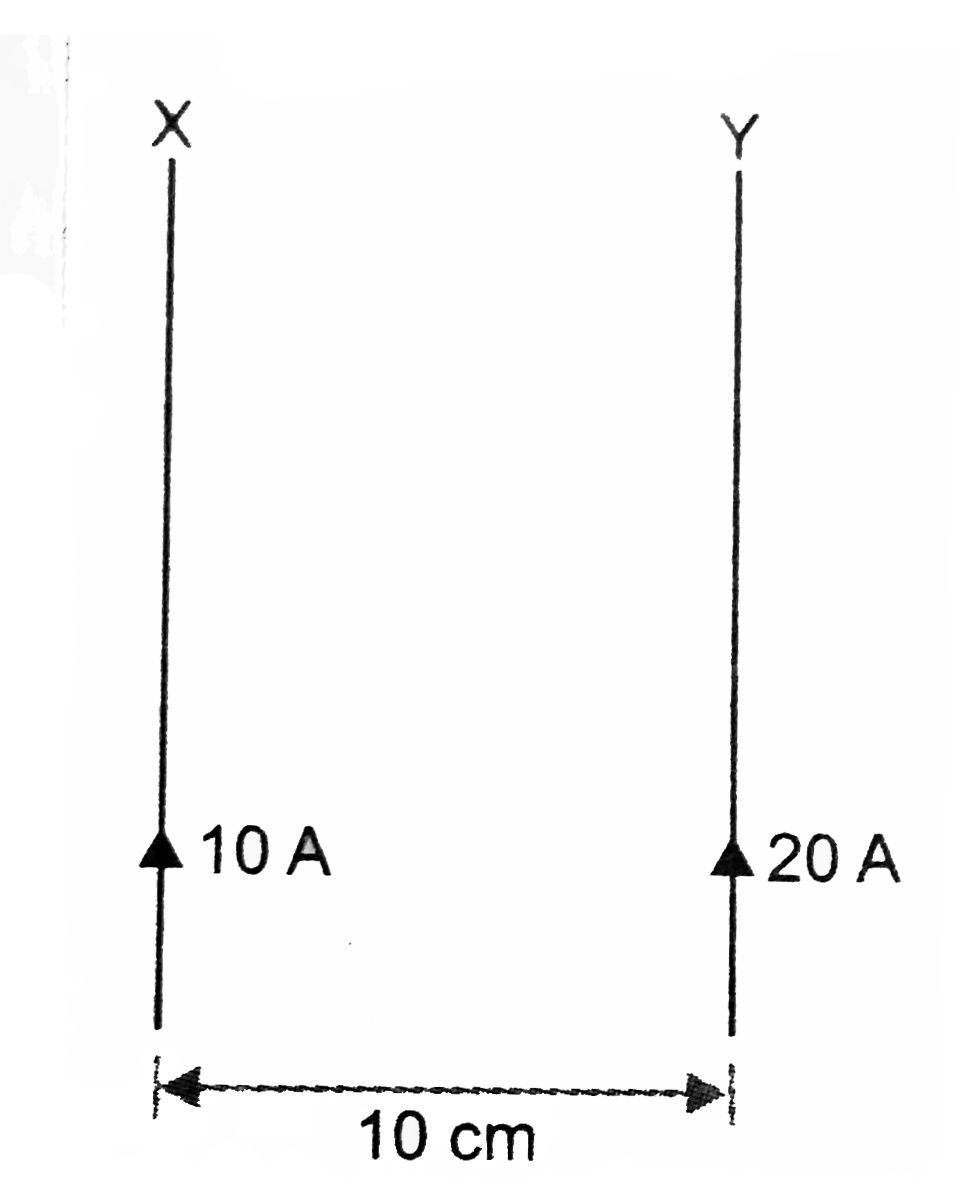
View SolutionA current of `1*0A` flowing in the sides of an equilateral triangle of side `4*5xx10^-2m`. Find the magnetic fied at the centroid of the triangle.
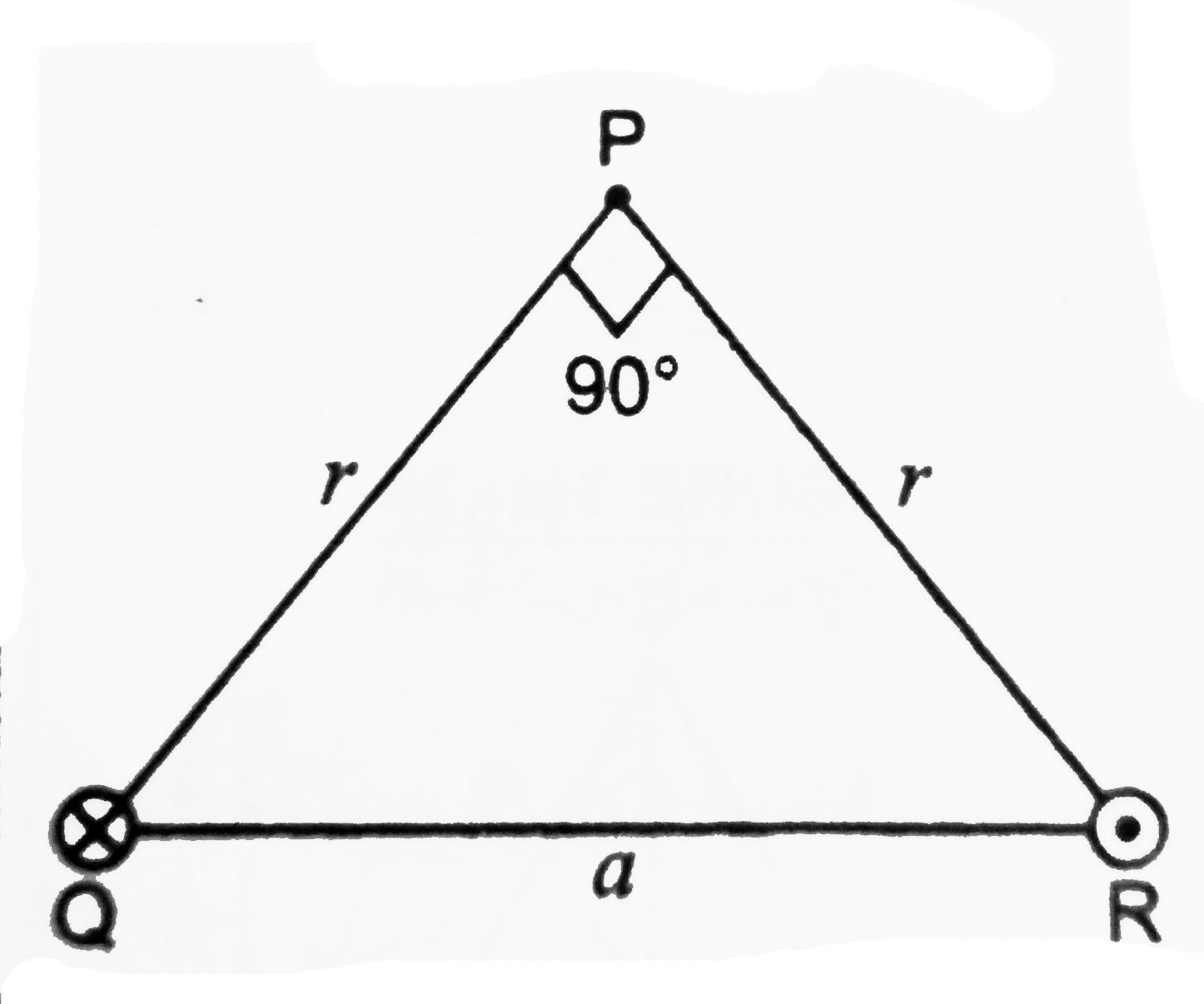
View SolutionFigure shows a right-angled isosceles `DeltaPQR` having its base equal to a. A current of I ampere is passing downwards along a thin straight wire cutting the plane of paper normally as shown at Q. Likewise a similar wire carries an equal current passing normally upwards at R. Find the magnitude and direction of the magnetic field induction B at P. Assume the wires to be infinity long.
View SolutionA straight wire carrying a current of `12A` is bent into a semicircular arc of radius `2*0cm` as shown in figure. Consider the magnetic field `vecB` at the centre of arc.
(a) What is the magnetic field due to the staight segments?
(b) In what way the contribution to `vecB` from the semicircle differs from that of a circular loop and in what way does it resemble?
(c) Would your answer be different if the wire were bent into a semicircle arc of the same radius but in the opposite way as shown in figure

View SolutionA tightly wound 100 turn coil of radius `10cm` is carrying a current of `1A`. What is the magnitude of the magnetic field at the centre of the coil?
View SolutionAn alpha particle is completing one circular round of radius `0*8m` in 2 seconds. Find the magnetic field at the centre of the circle. Electronic charge `=1*6xx10^(19)C`.
View SolutionThe electron in a hydrogen atom circles around the proton with a speed of `2*18xx10^6ms^-1` in an orbit of radius `5*3xx10^-11m`. Calcualte (a) the equivalent current (b) magnetic field produced at the proton. Given charge on electron `1*6xx10^-19C` and `mu_0=4pixx10^-7TmA^-1`.
View SolutionA circular loop of 2 turns carries a current of `5*0A`. If the magnetic field at the centre of loop is `0*40mT`, find the radius of the loop.
View SolutionA circular coil of `120` turns has a radius of `18cm` and carries a current of `3*0A`. What is the magnitude of the magnetic field (i) at the centre of the coil (ii) at a point on the axis of the coil at a distance from the centre equal to the radius of the coil?
View SolutionTwo identical circular oils of radius `0*2m` each having 30 turns are mounted coaxially `0*2m` apart. What is the magnetic field at the centre of each coil when a current of `0*6A` is passed through both the coils (a) in the same direction (b) in the opposite directions?
View SolutionTwo wires A and B have the same length equal to `44cm`. and carry a current of `10A` each. Wire A is bent into a circle and wire B is bent into a square. (a) Obtain the magnitudes of the fields at the centres of the two wires. (b) Which wire produces a greater magnetic field at the centre?
View SolutionThe wire shown in figure carries a current of `10A`. Determine the magnitude of the magnetic field at the centre O.
Given radius of the bent coil is `3cm`.

View SolutionTwo coaxial circular loops `L_1` and `L_2` of radii `3cm` and `4cm` are placed as shown in figure. What should be the magnitude and direction of the current in the loop `L_2` so that the net magnetic field at the point O be zero?

View SolutionIf a long horizontal conductor is bent as shown in figure and a current I is passed in it, find the magnitude and direction of magnetic field induction at the centre of circular part.
View SolutionThe current loop abcde formed by two circular segments of radii `r_1(=4cm)` and `r_2(=6cm)` with common centre at O, carries a current `I(=2A)` as shown in figure. What is the magnetic field at the common centre O? What will be the value of magnetic field at O when `theta=90^@`?
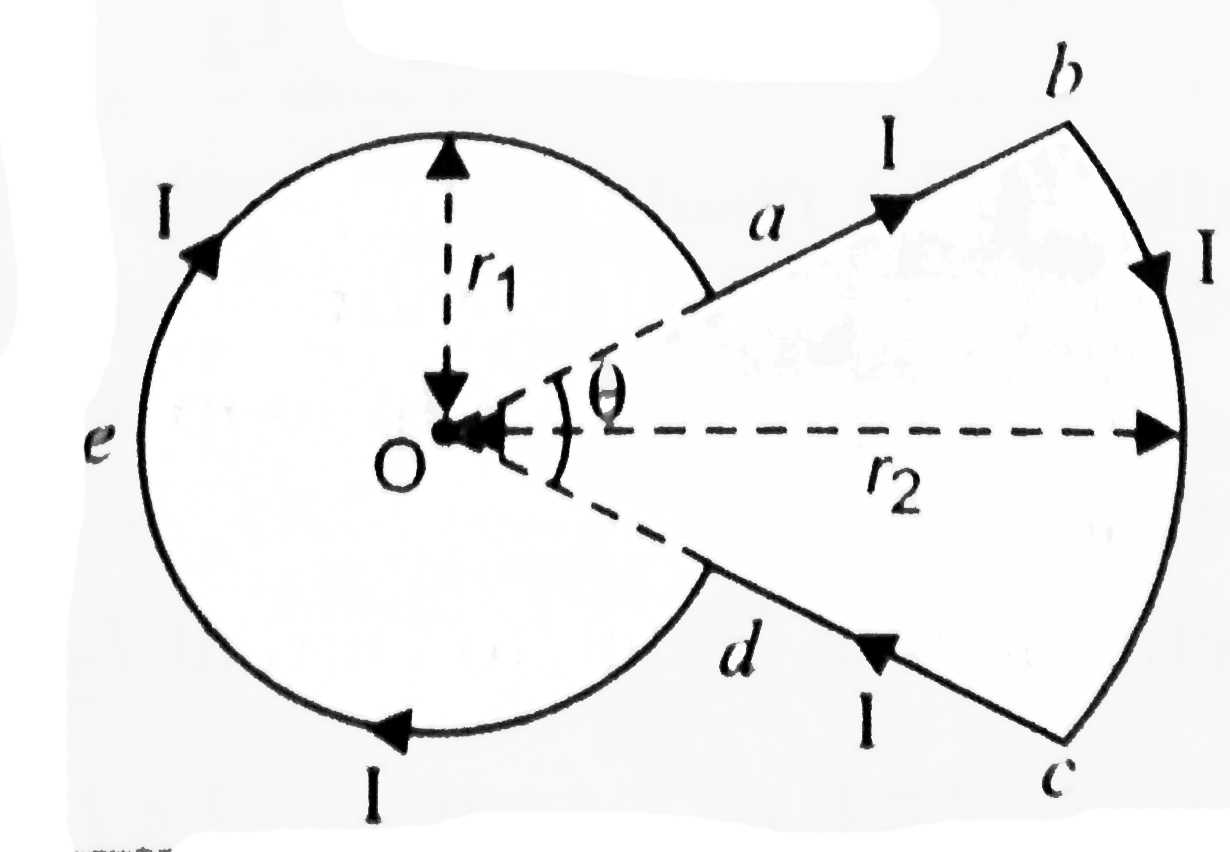
View SolutionFigure shows a long straight wire of circular crosssection (radius a) carrying steady current I. The current I is uniformly distributed across this crosssection. Calculate the magnetic field in the region `r lt a` and `r gt a`.

View SolutionA straight thick long wire of uniform cross-section of radius a is carrying a steady current I. Calculate the ratio of magnetic field at a point `a//2` above the surface of the wire to that at a point `a//2` below its surface. What is the maximum value of the field of this wire?
View SolutionA long straight solid conductor of radius `5cm` carries a current of `3A`, which is uniformly distributed over its circular cross-section. Find the magnetic field induction at a distance `4cm` from the axis of the conductor. Relative permeability of the conductor=1000.
View SolutionA wire of radius `0*8cm` carries a current of `100A` which is uniformly distributed over its cross-section. Find the magnetic field (a) at `0*2cm` from the axis of the wire (b) at the surface of the wire and (c) at a point outside the wire `0*4cm` from the surface of the wire. Neglect the permeability of the material of wire.
View SolutionA solenoid of length `0*5m` has a radius of `1cm` and is made up of `500` turns. It carries a current of `5A`. What is the magnitude of the magnetic field inside the solenoid?
View SolutionA solenoid coil of `300 turns//m` is carrying a current of `5A`. The length of the solenoid is `0*5m` and has a radius of `1cm`. Find the magnitude of the magnetic field well inside the solenoid.
View SolutionA solenoid of length `50cm`, having `100` turns carries a current of `2*5A`. Find the magnetic field, (a) in the interior of the solenoid, (b) at one end of the solenoid.
Given `mu_0=4pixx10^-7WbA^-1m^-1`.
View SolutionA copper wire having a resistance of `0*015Omega` per metre is used to wind a `500` turns solenoid of radius `1*0cm` and length `22cm`. If the e.m.f. of the battery used is `6V`, then find the magnetic field near the centre of the solenoid.
View SolutionA toroid has a core of inner radius `20cm` and outer radius `22cm` around which `4200` turns of a wire are wound. If the current in the wire is `10A`, what is the magnetic field
(a) inside the core of toroid (b) outside the toroid
(c) in the empty space surrounded by toroid?
View SolutionA coil wrapped around a toroid has inner radius of `15cm` and outer radius of `20cm`. If the toroid has `1000` turns of wire and carries a current of `12A`, find the maximum and minimum values of magnetic field within the toroid.
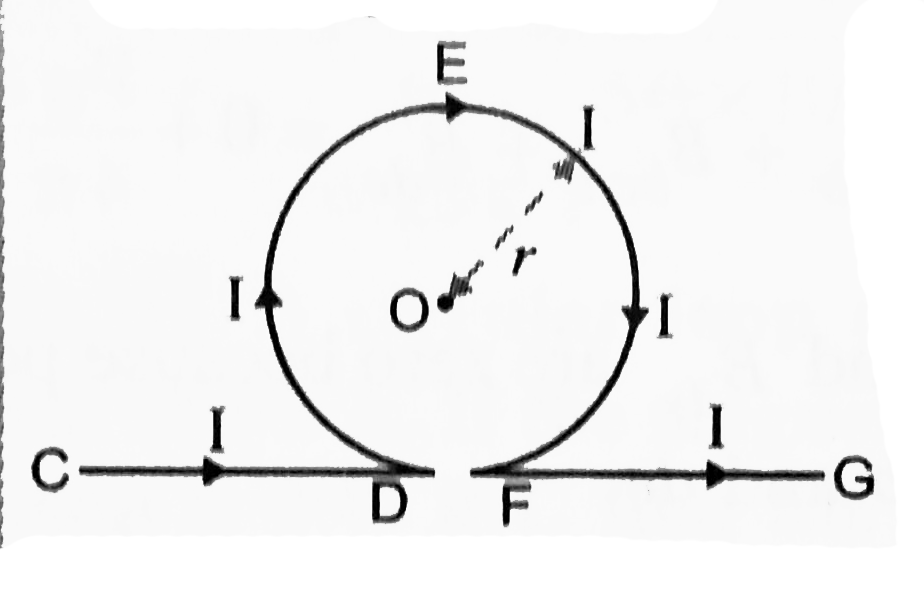
View SolutionIn figure bcdf is a circular coil of non-insulated thin uniform conductors, ab and de are very long straight parallel conductors, ab and de are very long straight parallel conductors, tangential to the coil at the points b and d. If the current `5A` enters the coil from a to b, find the magnetic field induction at O, the centre of the coil. The diameter of the coil is `10cm`.

View SolutionA very long wire carrying a current `I = 5.0 A` A is bent at right angles. Find the magnetic induction at a point lying on a perpendicular to the wire, drawn through the point of hending at a distance `l = 35 cm` from it.
View SolutionA beam of ions with velocity `2xx10^5ms^-1` enters normally into a uniform magnetic field of `0*04` tesla. If the specific charge of ion is `5xx10^7Ckg^-1`, find the radius of the circular path described.
View SolutionAn electron of mass `0*90xx10^-30kg`, under the action of magnetic field moves in a circle of radius `2*0cm` at a speed of `3*0xx10^6ms^-1`. If a proton of mass `1*8xx10^-27kg` were to move in a cirlce of the same radius in the same magnetic field, find its speed.
View SolutionAn `alpha`-particle is moving in a magnetic field of `(3hati+2hatj)` tesla with a velocity of `(5xx10^5hati)ms^-1`. What will be the magnetic force acting on the particle?
View SolutionThe magnetic flux density applied in a cyclotron is `3*5T`. What will be the frequency of electric field that must be applied between the dees in order (a) to accelerate protons (b) `alpha`-particles? mass of proton `1*67xx10^(-27)kg`.
View SolutionMagnetic field applied on a cyclotron is `0*7T` and radius of its dees is `1*8m`. What will be the energy of the emergent protons in `MeV`? Mass of proton`=1*67xx10^-27kg`.
View SolutionThe horizontal component of earth's magnetic field at a certain place is `3*0xx10^-5T` and the direction of the field is form the geographic south to the geographic north. A very long straight conductor is carrying a steady current of `1A`. What is the force per unit length on it when it is placed on a horizontal table and the diection of the current is (a) east to west (b) south to north?
View SolutionTwo straight wires A and B of lengths `10m` and `16m` and carrying currents `4*0A` and `5*0A` respectively in opposite directiions, lie parallel to each other `4*0cm` apart, Comute the force on a `10cm` long section of the wire B near its centre.
View SolutionA circular coil of `20turns` and radius `10cm` carries a current of `5A`. It is placed in a uniform magnetic field of `0*10T`. Find the torque acting on the coil when the magnetic field is applied (a) normal to the plane of the coil (b) in the plane of coil. Also find out the total force acting on the coil.
View SolutionA current of `300muA` deflects the coil of a moving coil galvanometer through `60^@`. What should be the current to cause rotation through `pi//5rad`? Determine the sensivity of this galvanometer.
View SolutionA galvanometer has a resistance of `50Omega`. A resistance of `5Omega` is connected across its terminals. What part of the total current will flow through the galvanometer?
View SolutionAn ammeter of resistance `0*80Omega` can measure current upto `1*0A`.
(a) What must be the value of shunt resistance to enable the ammeter to measure current upto `5*0A`?
(b) What is the combined resistance of the ammeter and the shunt?
View SolutionA galvanometer with a coil of resistance `12Omega` shows a full scale deflection for a current of `2*5mA`. How will you convert it into a voltmeter of range `7*5V`? Also, find the total resistance of voltmeter formed.
View SolutionA cathode ray tube contains a pair of parallel metal plates `1*0cm` apart and `3*0cm` long. A narrow horizontal beam of electrons with velocity of `3xx10^7ms^-1` is passed down the tube mid way between the two plates. When the potential difference of `550V` is maintained across the plates, it is found that the electron beam is so deflected that it just strikes the end of one of the plates. Find the specific charge of an electron.
View SolutionA proton enters a magnetic field of flux density `2*5T` with a speed of `1*5xx10^7ms^-1` at an angle of `30^@` with the field, Find the force on the proton.
View SolutionA charged particle of charge `2*0muC` moving along x-axis with a speed of `3xx10^6ms^-1` enters a magnetic field, `vecB=(0*3hatj+0*4hatk)` tesla acting in a specific. What is the magnitude of magnetic force on the charged particle?
View SolutionA copper has `8*0xx10^28` electrons per cubic metre. A copper wire of length `1m` and cross-sectional area `8*0xx10^-6m^2` carrying a current and lying at right angle to a magnetic field of strength `5xx10^-3T` experiences a force of `8*0xx10^-2N`. Calculate the drift velocity of free electrons in wire.
View SolutionAn electron travels in a circular path of radius `20cm` in a magnetic field `2xx10^-3T` (i) Calculate the speed of the electron (ii) What is the potential difference through which the electron must be accelerated to acquire this speed? Charge of electron `=1*6xx10^(-19)C`. Mass of electron `=9xx10^(-31)kg`.
View SolutionWhat is the radius of the path of an electron (mass `9xx10^(-31)kg` and charge `1*6xx10^(-19)C`) moving at a speed of `3xx10^7ms^-1` in a magnetic field of `6xx10^-4T` perpendicular to it? What is its frequency? Calcualte its energy in `keV`.
View SolutionA proton is travelling with horizontal velocity `v_x=2*5xx10^8cms^-1`. Calculate the transverse deflection in travelling horizontal distance, `x=5cm` in electric field of `E_y=400V//cm`. Mass of proton, `m=1*6xx10^(-24)g`, charge on proton, `e=1*6xx10^(-19)C`.
View SolutionAn electron of energy `2000eV` describes a circular path in magnetic field of flux density `0*2T`. What is the radius of the path? Take `e=1*6xx10^(-19)C`, `m=9xx10^(-31)kg`.
View SolutionA proton, a deutron and `alpha`-particle, whose kinetic energies are same, enter perpendicularly a uniform magnetic field. Compare the radii of their circualr paths.
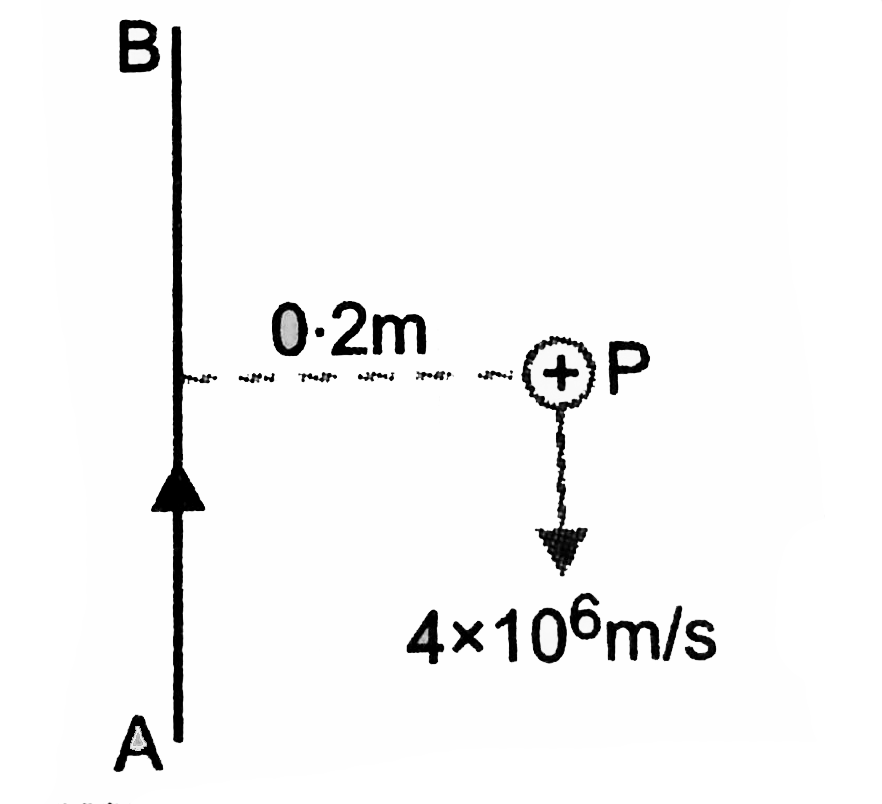
View SolutionA long straight wire AB carries a current of `4A`. A proton P travels at `4xx10^6ms^-1` parallel to the wire, `0*2m` from it and in a direction opposite to the current as shown in figure. Calculate the force which the magnetic field of current exerts on the proton. Also specify the direction of the force.
View SolutionA solenoid of length `1*5m` has a radius of `1*5cm` and has a total of `1500` turns wound on it. It carries a current of `3A`. Calculate the magnetic of the axial magnetic field inside the solenoid. If an electron were to move with a speed of `2xx10^4ms^-1` along the axis of the current carrying solenoid, what would be the force experienced by this electron?
View SolutionAn electron moving horizontally with a velocity of `4xx10^4ms^-1` enters a region of uniform magnetic field of `10^-5T`, acting vertically downwards as shown in figure. Draw its trajectory and find out the time it takes to come out of the region of magnetic field.

View SolutionIn a chambe of a uniform magnetic field of `8*0G[1G=10^-4T]` is maintained. An electron with a speed of `4*0xx10^6ms^-1` enters the chamber in a direction normal to the field
(i) Describe the path of electron.
(ii) What is the frequency of revolution of electron?
(iii) What happens to the path of the electron if it progressively loses its energy due to collisions with the atoms or molecules of the environment?
View SolutionA beam of electrons enters a uniform magnetic field of `0*3T` with a velocity of `4xx10^5ms^-1` at an angle of `60^@` to the field. Find the radius of the helical path taken by the beam. Also find the pitch of the helix (distance travelled by a proton parallel to the magnetic field during one period of rotation). Mass of proton is `1*67xx10^(-27)kg`.
View SolutionA beam of alpha particle passes underflected with a horizontal velocity v, through a region of electric and magnetic fields, mutually perpendicular to each other and normal to the direction of the beam. If the mangnitude of the electric and magnetic fields are `120kVm^-1` and `60mT` respectively, calculate (i) velocity of the beam (ii) force with which it strikes a target on a screen, if the alpha particle beam current is equal to `1mA`? Mass of proton=mass of neutron `=1*675xx10^(-27)kg`.
View SolutionA cyclotron oscillator frequency is `10MHz`. What should be the operating magnetic field for accelerating protons? If the radius of its dees is `60cm`, what is the kinetic energy of the proton beam produced by the acceleration in `MeV`?
`(e=1*6xx10^(-19)C, m_p=1*67xx10^(-27)kg, 1MeV=1*6xx10^(-13)J)`
View SolutionAn electron beam passes through a magnetic field of `4xx10^-3 weber//m^2` and an electric field of `2xx10^4Vm^-1`, both acting simultaneously. The path of electron remaining undeviated, calcualte the speed of the electrons. If the electric field is removed, what will be the radius of the electron path?
View SolutionA cyclotron oscillator frequency is `10MHz`. What should be the operating magnetic field for accelerating `alpha`-particle? If the radius of the dees is `50cm`, what is the kinetic energy in `MeV` of the `alpha`-particle beam produced by the accelerator?
`(e=1*6xx10^(-19)C, m_alpha=4*0028 a.m.u., 1a.m.u.=1*66xx10^(-27)kg)`
View SolutionIn a cycloton, the protons are to be accelerated with a magnitude field of magnitude `1*5T`. How rapidly should the electric field between the dees be reversed? Mass and charge of proton are `1*67xx10^(-27)kg` and `1*6xx10^(-19)C` respectively.
View SolutionIf the maximum value of accelerating potential provided by a radio frequency oscillator be `25kV`, find the number of revolutions made by a proton in a cyclotron to achieve one sixth of the speed of light. Mass of proton `=1*67xx10^(-27)kg`.
View SolutionThe horizontal component of earth's magnetic field at a certain place is `3*0xx10^-5T` and the direction of the field is form the geographic south to the geographic north. A very long straight conductor is carrying a steady current of `1A`. What is the force per unit length on it when it is placed on a horizontal table and the diection of the current is (a) east to west (b) south to north?
View SolutionA wire carrying a current `15A` and of length `4*0cm` is placed inside a solenoid near its centre making an angle of `60^@` with the axis of solenoid, where the magnitude of the magnetic field due to the solenoid is `0*30T`. What is the force on the wire?
View SolutionA straight wire `50cm` long carries a current of `5A`. It is placed at right angle to a uniform magnetic field of `1T`. Find the mechanical force on the wire and the power required to move it at `10ms^-1` in a plane at right angles to the magnetic field.
View SolutionA straight wire of mass 200 g and length 1.5 m carries a current of 2 A. It is suspended in mid-air by a uniform horizontal magnetic field B. What is the magnitude of the magnetic field?

View SolutionA long straight conductor C carrying a current of `3A` is placed parallel to a short conductor D of length `5cm`, carrying a current `4A`. The two conductors are `10cm` apart. Find (i) the magnetic field due to C at D. (ii) The approximate force on D.
View SolutionA horizontal wire `0*2m` long carries a current of `4A`. Find the magnitude and direction of the magnetic field, which can support the weight of the wire. Given, the mass of the wire is `3xx10^-3kg//m`, `g=10ms^-2`.
View SolutionA straight horizontal conducting rod of length `0*60m` and mass of `60g` is suspended by two vertical wires at its ends. A current of `5*0A` is set up in the rod through the wire. (a) What magnetic field should be set up normal to the conductor in order that the tension in the wire is zero?
(b) What will be total tension in the wires if the direction of current is reversed, keeping the magnetic field same as before (Ignore mass of the wire), `g=10ms^-2`.
View SolutionCalculate the force per unit length on a long straight wire carrying current `4A` due to parallel wire carrying current `6A` current. Distance between the wires `=3cm`.
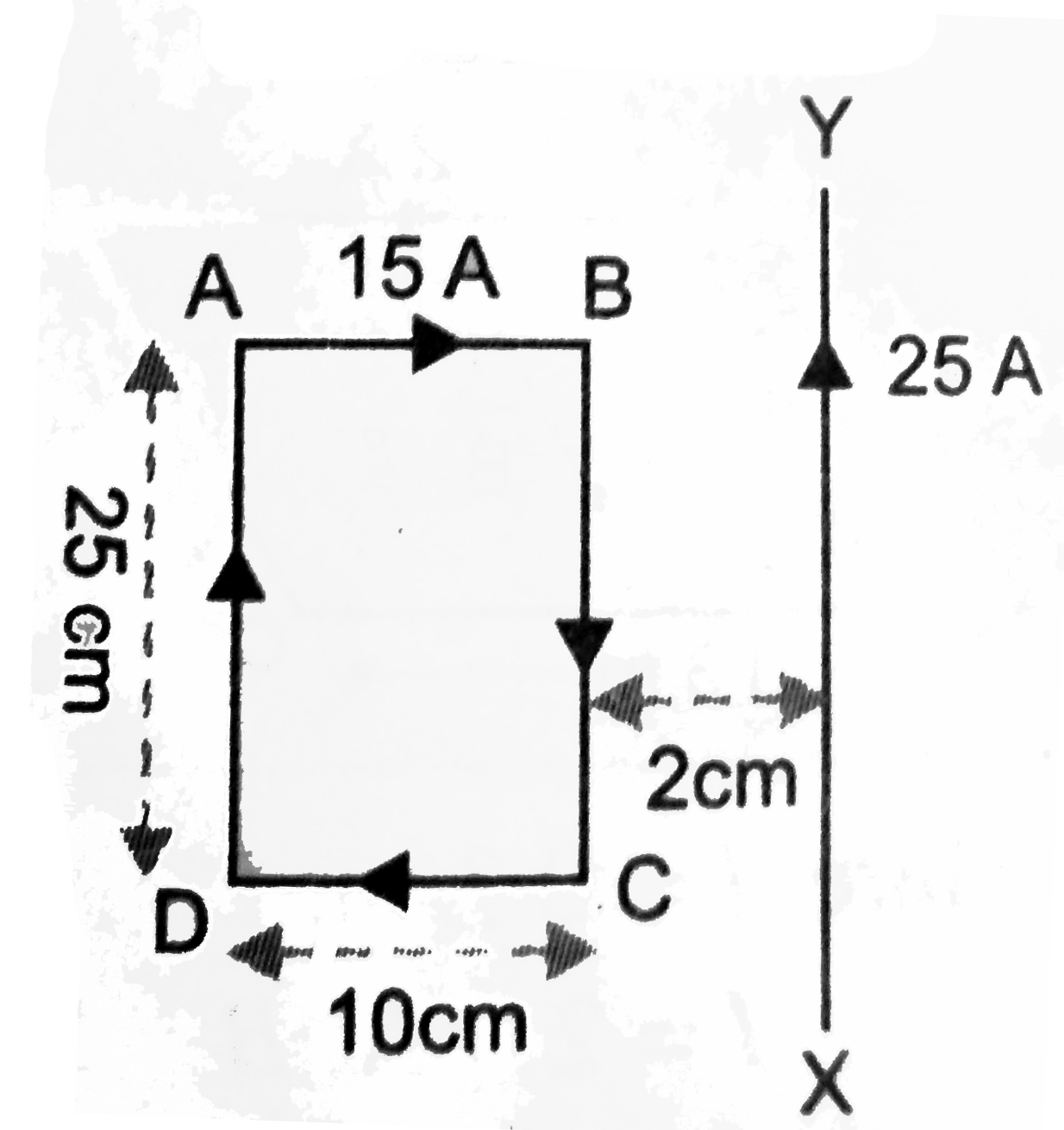
View SolutionFigure shows a rectangular current-carrying loop placed `2cm` away from a long, straight, current carrying conductor. What is the direction and magnitude of the net force acting on the loop?
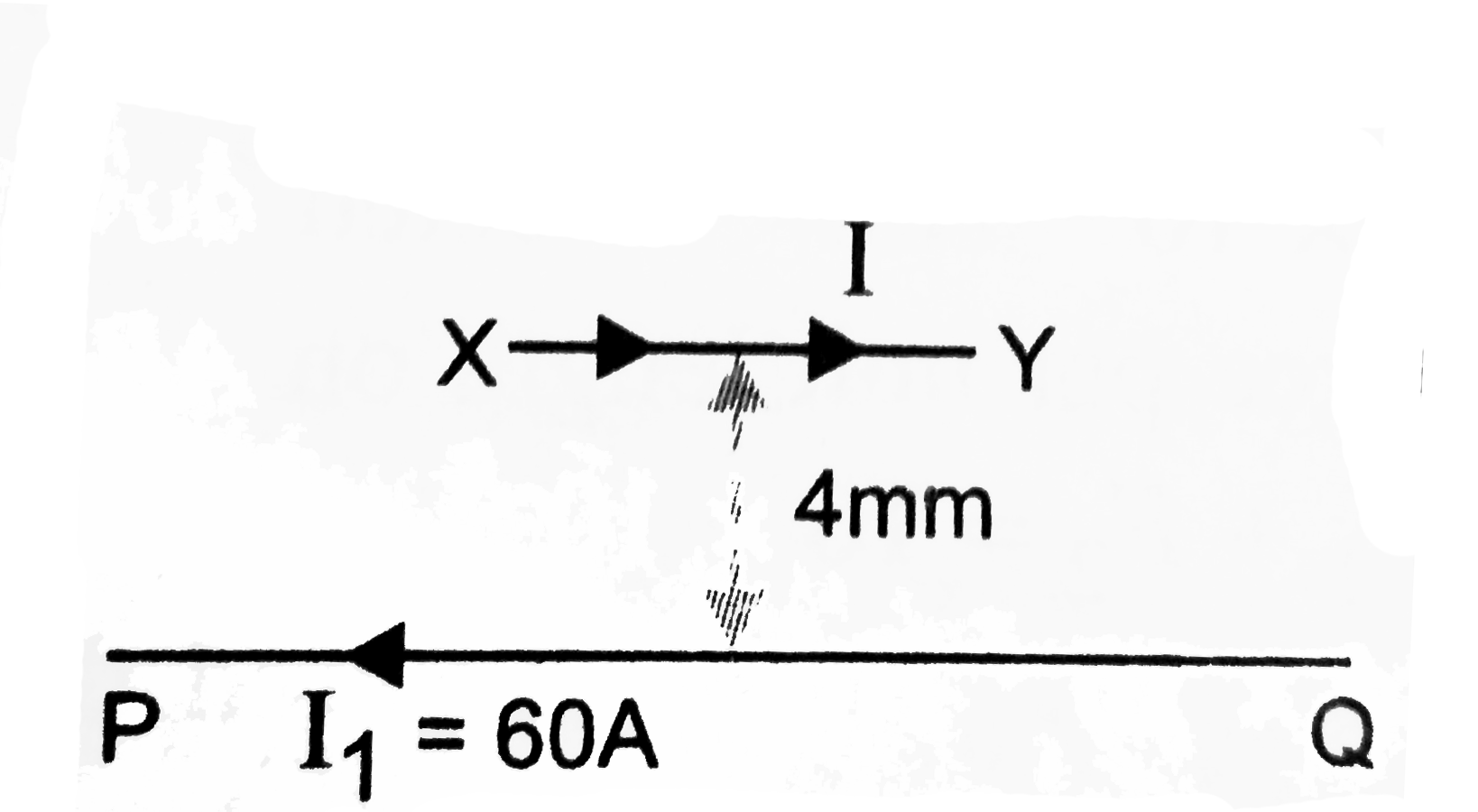
View SolutionA long straight conductor PQ, carrying a current of `60A`, is fixed horizontally. Another long conductor XY is kept parallel to PQ at a distance of `4mm`, in air. Conductor XY is free to move and carries a current I. Calcualte the magnitude and direction of current I for which the magnetic repulsion just balances the weight of conductor XY. (Mass per units length for conductor XY is `10^-2kg//m`).
View SolutionFigure shows a part of an electric circuit. The wires AB, CD, and EF are long and have identical resistances. The separation between the neighbouring wires is 1.0 cm. The wires AE and BF have negligible resistances and the ammeter reads 30 A . Calculate the magnetic force per unit length of AB and CD. `

View SolutionA wire AB is carrying a steady current of `12A` and is lying on the table. Another wire CD carrying current `5A` is held vertically above AB at a height of 1mm. Find the mass per unit length of the wire CD so that it remains suspended at the position when left free. Give the direction of the current flowing in CD with respect to that in AB. `g=10ms^-2`.
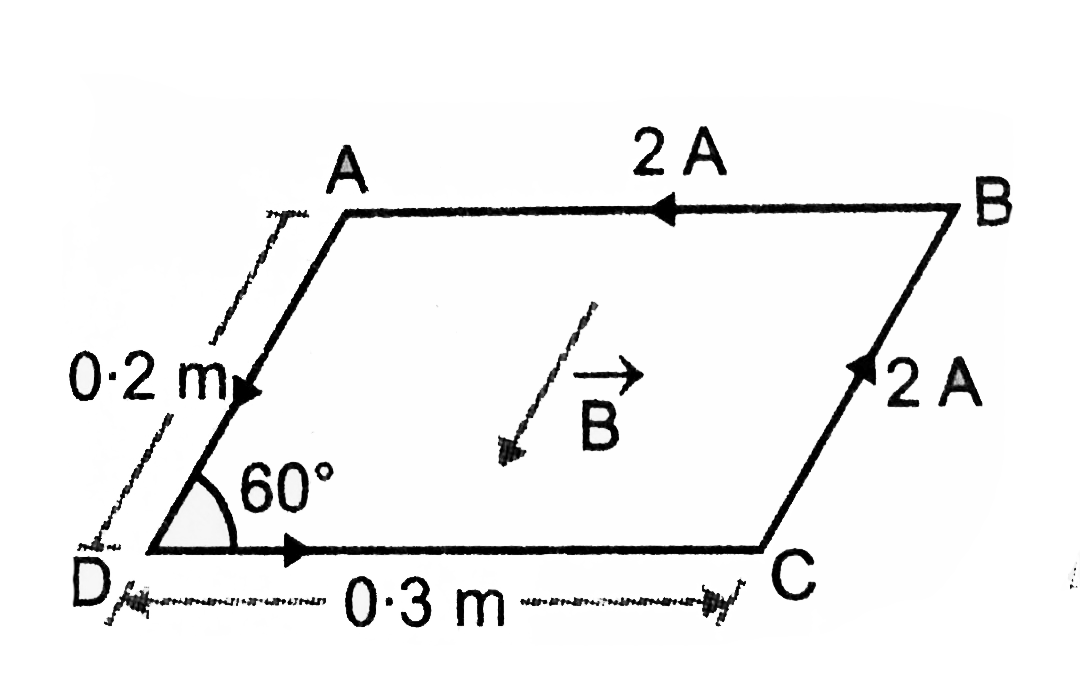
View SolutionA parallelogram shaped coil ABCD of sides `0*3m` and `0*2m` carries a current of `2*0A` as shown in figure. It is placed in a uniform magnetic field `vecB=50T` parallel to AD. Find (i) forces on the sides of the coil and (ii) torque on the coil.
View SolutionA square shaped plane coil of area `100cm^2` of `200` turns carries a steady current of `5A`. It is placed in a uniform magnetic field of `0*2T` acting perpendicular to the plane of the coil. Calculate the torque on the coil when its plane makes an angle of `60^@` with the direction of the field. In which orientation will the coil be in stable equilibrium?
View SolutionA solenoid of length `0*4m` and having `500` turns of wire carries a current of `3A`. A thin coil having 10 turns of wire and of radius `0*01m` carries a current of `0*4A`. Calculate the torque required to hold the coil in middle of the solenoid with its axis perpendicular to the axis of the solenoid.
`(mu_0=4pixx10^-7V-s//A-m)`
View SolutionA 100 turn closely wound circular coil of radius `10cm` carries a current of `3*2A`. (i) What is the field at the centre of the coil? (ii) What is the magnetic moment of this arrangement? The coil is placed in a vertical plane and is free to rotate about a horizontal axis which coincides with its diameter. A uniform magnetic field of `2T` in the horizontal direction exists such that initially the axis of the coil is in the direction of the field. The coil rotates through an angle of `90^@` under the influence of the magnetic field. (iii) What are the magnitudes of the torques on the coil in the initial and final positions? (iv) What is the angular speed acquired by the coil when it has rotated by `90^@`? The moment of inertia of the coil is `0*1kgm^2`.
View SolutionA rectangular coil of sides `8cm` and `6cm` haivng 2000 turns and carrying a current of `200mA` is placed in a uniform magnetic field of `0*2T` directed along the positive x-axis. (a) What is the maximum torque the coil can experience? In which orientation does it experience the maximum Torque? (b) For which orientations of the coil is the torque zero? When is this equilibrium stable and unstable?
View SolutionA rectangular coil of area `5.0xx10^(-4) m^2` and 60 turns is pivoted about one of its vertical sides. The coil is in a radial horizontal field of 90 G (radial here means the field liners are in the plane of the coil for any rotation). What is the torsional constant of the hair spring connected to the coil if a current of 2.0 mA produces an angular deflection of `18^@`?
View SolutionCompare the current sensitivity and voltage sensitivity of the following moving coil galvanometers:
Meters A : `n=30, A=1*5xx10^-3m^2`,
`B=0*25T, R=20Omega`
Meter B: `n=35, A=2*0xx10^-3m^2`,
`B=0*25T, R=30Omega`.
You are given that the springs in the two meters have the same torsional constants.
View SolutionA current of `300muA` deflects a coil of a moving coil galvanometer through `30^@`. What should be the current to cause the rotation through `pi//5` radius? What is the current sensitivity of the galvanometer ? If resistance of galvanometer is `50Omega`, find its voltage sensitivity.
View SolutionThe current sensitivity of a moving coil galvanometer increases by `20%` when its resistance is increased by a factor 2. Calculate by what factor does the voltage sensitivity change?
View SolutionA current of `500muA` deflects the coil of a moving coil galvanometer through `60^@`. What should be the current to cause the rotation through `pi//5` radian? What is the sensitivity of galvanometer?
View SolutionWhen a galvanometer having 30 divisions scale and `100Omega` resistance is connected in series with the battery of e.m.f. 3 volt through a resistance of `200Omega`, it shows full scale deflection. Find the figure of merit of the galvanometer in microampere.
View Solution
Solved Examples questions and complete solutions for chapter MAGNETIC EFFECT OF CURRENT AND MAGNETISM of PRADEEP PHYSICS (HINGLISH) of Class 12
All Exercises from PRADEEP Class 12 PHYSICS MAGNETIC EFFECT OF CURRENT AND MAGNETISM
- Competition Focus (Multiple Choice Questions)
- Conceptual Problems (d)
- Exercise
- Fill in the blank (a)
- Fill in the blank (b)
- Fill in the blank (c)
- NCERT Exemplar Problems (Chapter 5 Short Answer Questions)
- Short Answer Questions (b)
- Solved Examples
- Test Your Grip (a)
- Test Your Grip (c)
- Test Your Grip (d)
- Value Based Questions
- Very Short Answer Questions (a)