Complete Solutions to Exercise of chapter MAGNETIC EFFECT OF CURRENT AND MAGNETISM of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MAGNETIC EFFECT OF CURRENT AND MAGNETISM |
| PRADEEP | Exercise |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
The magnetic field at a perpendicular distance of `2cm` from an infinite straight current carrying conductor is `2xx10^-6T`. The current in the wire is
View SolutionA positive charge is moving towards an observer. The direction of magnetic induction lines is
View SolutionThe wire shown in figure carries a current of `10A`. Determine the magnitude of the magnetic field at the centre O.
Given radius of the bent coil is `3cm`.

View SolutionIf a long hollow copper pipe carriers a direct current, the magnetic field associated with the current will be:
View SolutionA current carrying wire produces in the neighbourhood
View SolutionA circular coil of n turns and radius r carries a current I. The magnetic field at the center is
View SolutionA thin ring of radius `R` metre has charge `q` coulomb uniformly spread on it. The ring rotates about its axis with a constant frequency of `f` revolution/s. The value of magnetic induction in `Wb m^(-2)` at the centre of the ring is
View SolutionA small coil of `N` turns has area `A` and a current `I` flows through it. The magnetic dipole moment of this coil will be
View SolutionA circular coil carrying current behaves as a
View SolutionA long solenoid has n turns per metre and current IA is flowing through it. The magnetic field induciton at the ends of the solenoid is
View SolutionTwo particles A and B having equal charges `+6C`, after being accelerated through the same potential differences, enter a region of uniform magnetic field and describe circular paths of radii `2cm` and `3cm` respectively. The ratio of mass of A to that of B is
View SolutionAn electron is moving at a speed of `100ms^-1` along the x-axis through uniform electric and magnetic fields. The magnetic field is directed along z-axis and has magnitude `5*0T`. In unit vector notation, what is the electric field?
View SolutionThe force between two parallel current carrying wires is independent of
View SolutionA straight conductor is placed along the axis of a circular coil perpendicular to the plane of the coil. Then electric current is passed through both,
View SolutionThe force experienced by a wire of length `10cm` kept at an angle of `30^@` to a uniform magnetic field of `0*5T` and carrying a current of `6A` is
View SolutionA rectangular coil of turns `500` and area `2cmxx1cm` carries `100mA` current. It is suspended in a uniform magnetic field of `10^-3T`, so that its plane makes an angle `60^@` with it. The torque on the coil in N-m is
View SolutionTo protect galvanometer from possible damages due to large current, which of the following is connected to its coil:
View SolutionTo convert galvanometer into ammeter which one of the following is connected with the coil:
View SolutionAn ammeter reads upto 1 ampere. Its internal resistance is 0.81 ohm. To increase the range to 10 A the value of the required shunt is
View SolutionA galvanometer has a resistance of `30Omega` and a current of `2*0mA` gives full scale deflection. How will you convert this galvanometer into a voltmeter of `0*2` volt range?
View SolutionChoose the correct statement.
View SolutionThe ratio of the shunt resistance and the resistance of a galvanometer is `1*499`. If the full scale deflection current of the galvanomter is `2mA`, the range of ammeter is
View SolutionWhen distance between two given magnetic poles is halved, force between them becoems k times, where `k=`
View SolutionWhat is not true about poles of a magnet?
View SolutionSI unit of magnetic pole strength is
View SolutionMagnetic moment of a current loop becomes k times when diameter of loop is made twice and number of turns is made three fold where, `k=`
View SolutionMagnetic field strength due to a bar magnet at a point distant d from the center of magnet
View SolutionTorque acting on a magnet held at angle `theta` with a magnetic field is maximum, where `theta=`
View SolutionIn the potential energy of magnetic dipole is zero when `theta=`
View SolutionThe small angle between magnetic axis and geographical axis at a place is called
View SolutionHorizontal component of earth at a place is `3*2xx10^-5T`, and angle of dip is `60^@`. The resultant intensity of earth's field at the place is
View SolutionThe correct value of Bohr magneton is
View SolutionChoose the diamagnetic material out of the following
View SolutionFor a paramagnetic substance
View SolutionFor a paramagnetic substance
View SolutionCurie temperature is the temperature above which
View SolutionBiot Savart's law deals with the magnetic field induction at a point due to a………………. .
View SolutionThe direction of magnetic field lines due to straight conductor carrying current is given by……………….. .
View SolutionIf current through a circular coil flows in clockwise direction, then the direction of magnetic field at the centre of the circular coil is………………to the plane of the coil, directed……………. .
View SolutionThe magnetic dipole moment of a current loop, carrying current I, having n turns, each of radius r is………………….. .
View SolutionThe magnetic field induction is……………..for a point on the surface of solid cylinder carrying current and is………………….for a point on the axis of the cylinder.
View SolutionAmpere's law is applicable for………………..current distribution whereas the Biot Savart's law is applicable for………………..current distribution.
View SolutionIf a charged particle is describing a circular path of radius r under the effect of perpendicular electric field, (i.e., motion of an electron around the nucleus of an atom) the force on the charged particle is……………..proportional to the …………..of radius of the circular path.
View SolutionWhen a charged particle is projected perpendicular to the magnetic field, the force acting on the charged particle is……………of the radius of circular path but…………….the speed of the charged particle.
View SolutionThe force on a wire carrying of any shape in a uniform field is…………….of its shape but……………………..on the vector length joining the beginning and ending of the current carrying wire.
View SolutionThe two linear parallel conductors carrying currents in the opposite direction…………………each other.
View SolutionA linear conductor carrying if placed parallel to the direction of magnetic field, it experiences …………………….force.
View SolutionWhen a coil carrying current is set with its plane perpendicular to the direction of magnetic field, then torque on the coil is……………. .
View SolutionThe magnetic field lines of a magnet form……………….loops unlike………………field lines.
View SolutionAccording to Gauss's law for magnetism, …………………..through any closed surface is…………………………. .
View SolutionMagnetic inclination at a place is the angle which the……………………makes with………………in……………… .
View SolutionIsogonic lines are the lines joining places of…………………….. .
View SolutionIn the northern hemisphere, magnetic lines of force due to earth's field point ………………………… .
View SolutionAt a particular place, horizontal and vertical components of earth's magnetic field are equal. The angle of dip at that place is…………… .
View SolutionBohr magneton is the …………………. magnetic dipole moment associated with …………….. due to orbital motion of ……………. in the stationary orbit of the atom.
View SolutionRelative magnetic permeability of a material is defined as the ratio of ………………….to……………….of…………… .
View SolutionMagnetic field strength, ………………., flux …………………represents the same quantity.
View SolutionSI units of magnetic permeability are …………………….., ……………………, …………………….. .
View SolutionMagnetic moment per unit volume of the material is called ……………. of the material.
View SolutionIntensity of magnetisation of a magnetic material is defined as ……………..per unit……………..of the material.
View SolutionUnits of magnetising intensity and intensity of magnetisation are…………………., i.e., ………………… .
View SolutionIndividual atoms/molecules/ions of a diamagnetic substance………….any net………………..on their own.
View SolutionSuperconductors are the most exotic………………..materials. Infact, ………………….conductivity and perfect………………go together.
View SolutionAccording to Curie law in magnetism, ………………..of a magnetic material varies……………..as the …………………….of the material.
View SolutionAn element `Deltavecl=Deltaxhati` is placed at the origin as shown in figure and carries a current `I=2A`. Find out the magnetic field at a point P on the y-axis at a distance of `1*0m` due to the element `Deltax=1cm`. Give also the direction of the field produced.
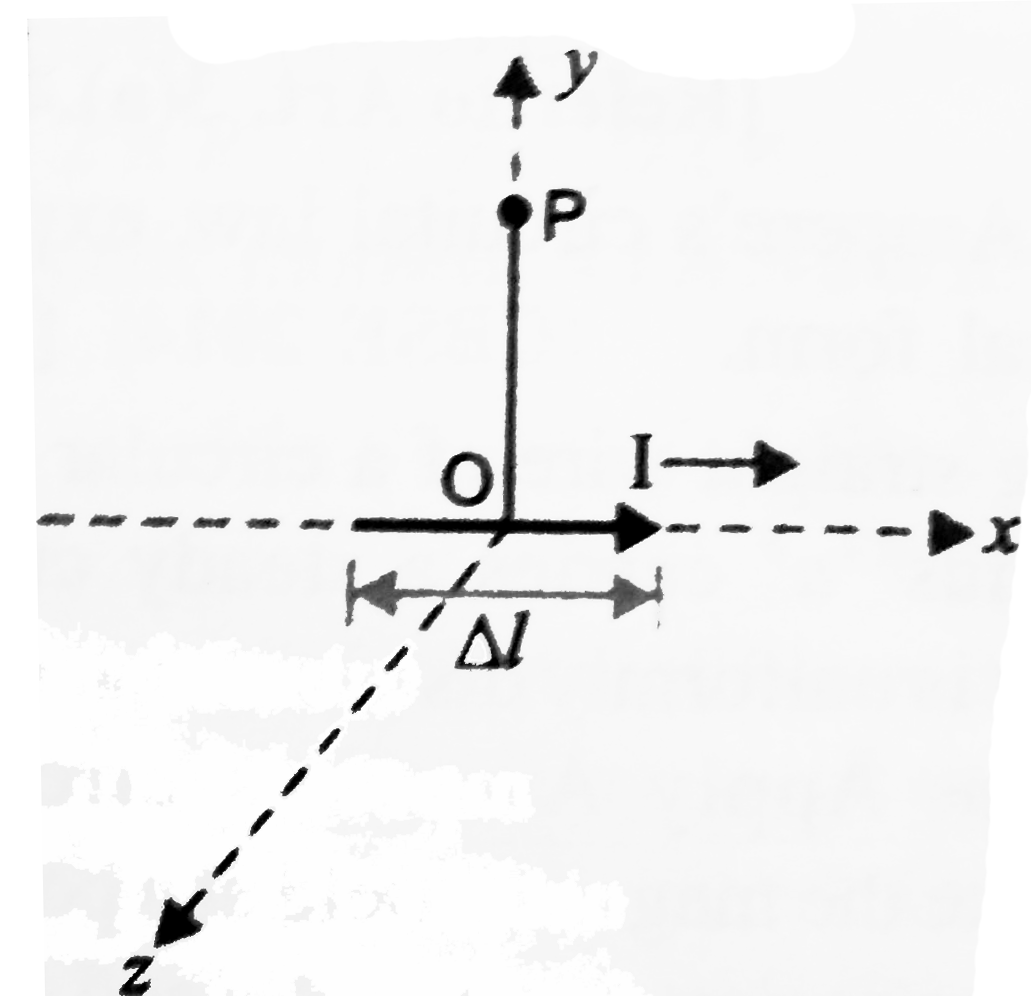
View SolutionA wire placed along north-south direction carries a current of `5A` from south to north. Find the magnetic field due to a `1cm` piece of wire at a point `200cm` north east from the piece.
View SolutionA current of `10A` is flowing east to west in a long wire kept in the east-west direction. Find magnetic field in a horizontal plane at a distance of (i) `10cm`. North (ii) `20cm` south from the wire, and in a vertical plane at a distance of (iii) `40cm` downwards, (iv) `50cm` upwards.
View SolutionCalculate the magnetic field induction at the center of the coil in the form of a square of side `10cm`, carrying a current of `10A`.
View SolutionWhat current must flow in an infinitely long straight wire to produce a magnetic field of `4xx10^5T` at `8cm` away from the wire?
View SolutionTwo long parallel wires are placed at a distance of `12cm` from each other in air. Each wire has a current of `3A`. Calculate the magnetic field at a point mid way between them when the currents in them are : (i) in the same direction and (ii) in opposite direction.
View SolutionA long straight wire carrying a current of `25A` is placed in an external uniform magnetic field `3*0xx10^-4T` parallel to the current. Find the magnitude of the resultant magnetic field at a point `1*5cm` away from the wire.
View SolutionFind the magnetic field B at the center of a rectangular loop of length l and width b, carrying a current i.
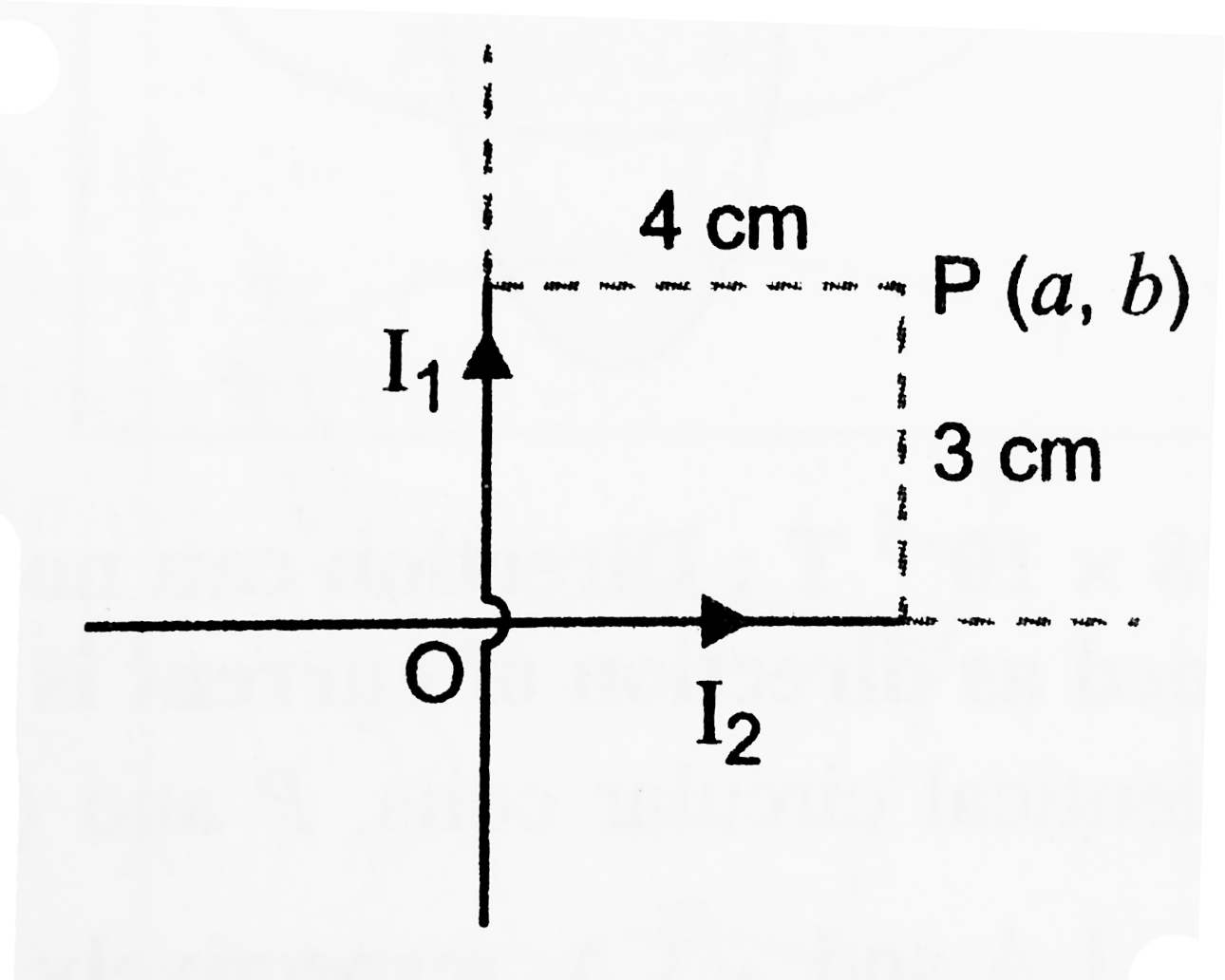
View SolutionTwo insulating infinite long conductors carrying currents `I_1(=2A)` and `I_2(=4A)` lie mutually perpendicular to each other in the same plane, as shown in figure. Find the magnetic field at the point P(a,b), where `a=4cm`, , `b=3cm`.
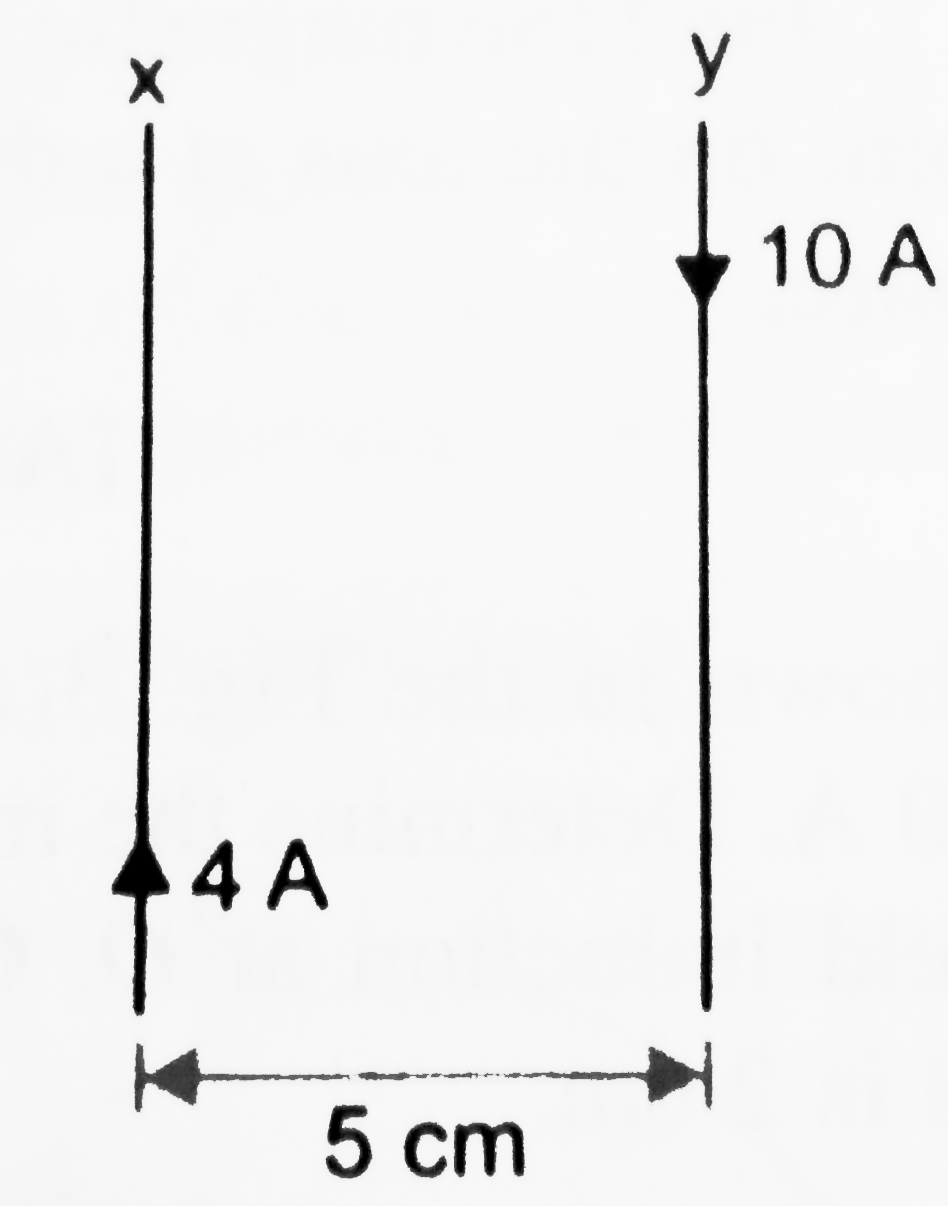
View SolutionFigure shows two long parallel straight wires distance 5cm apart carrying currents `4A` and `10A` in opposite directions. Find the position of a point where the resultant magnetic field due to current in two wires in zero.
View SolutionEqual currents `i=1` A are flowing through the wires parallel to y-axis located at `x=+1m, x=+2m, x=+4m` and so on...., etc. but in opposite directions as shown in Fig The magnetic field (in tesla) at origin would be

View SolutionA straight wire of length `pi//2` meter, is bent into a circular shape. If the wire were to carry a current of `5A`, calculate the magnetic field, due to it, before bending, at a point distance `0*01` times the radius of the circle formed from it. Also calculate the magnetic field, at the centre of the circular loop formed, for the same value of current.
View SolutionThe electron of hydrogen atom moves along a circular path of radius `0*5xx10^(-10)m` (i) with a speed of `4*0xx10^6ms^-1`. (ii) with a frequency `6*8xx10^(15)Hz`. Calculate the magnetic field produced at the centre of the circular path.
`(e=1*6xx10^(-19)C)`.
View SolutionCalculate the magnetic field due to a circular coil of `250` turns and of diameter `0*1m`, carrying a current of `7A` (i) at the center of the coil (ii) at a point on the axis of the coil at a distance `0*12m` from the center of the coil.
View SolutionThe magnetic field due to a current-carrying circular loop of radius `10cm` at its centre is `0*60xx10^-4T`. Find the magnetic field due to this loop at a point on the axis at a distance of `4cm` from the centre.
View SolutionThe wire shown in the figure, carries a current of `60A`. Determine the magnitude of the magnetic field induction at O. Given radius of the bent coil is `2cm`.
View SolutionAn alpha particle moves along a circular path of radius `2Å` with a uniform speed of `2xx10^6ms^-1`. Calculate the magnetic field set up at the center of circular path.
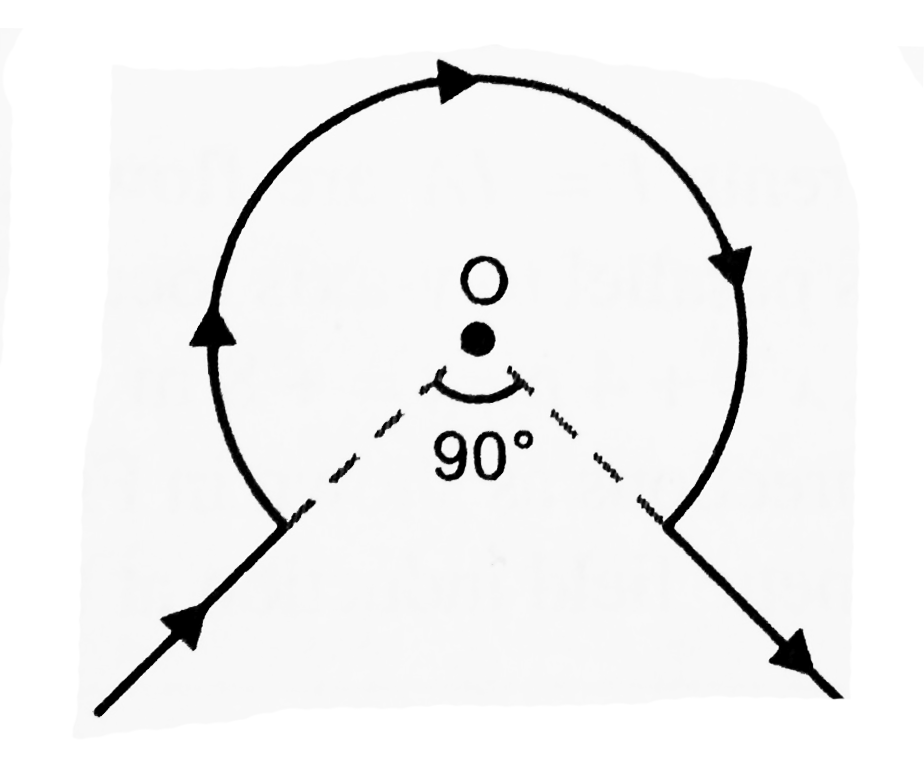
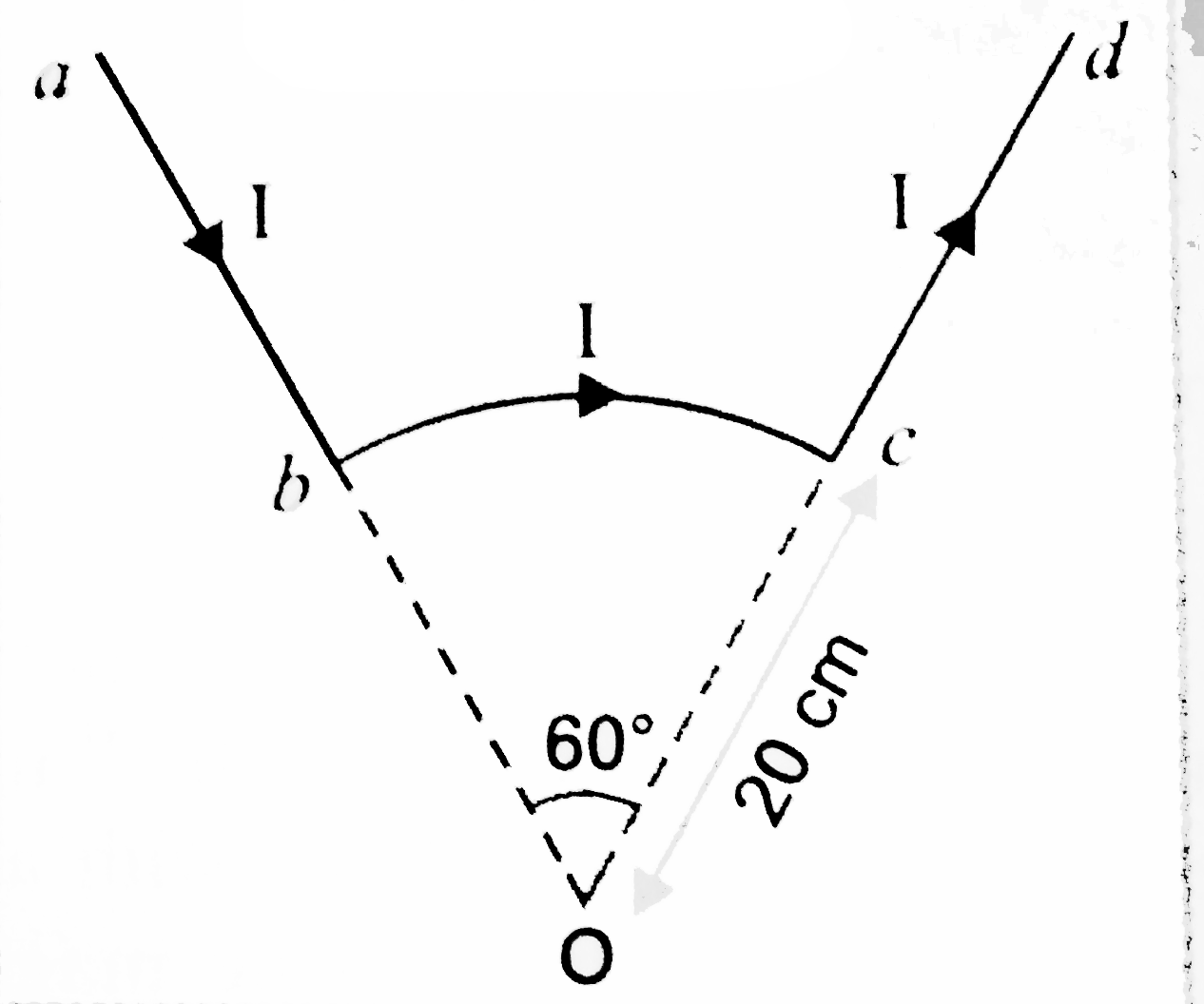
View SolutionA circular segment of radius `20cm` subtends an angle of `60^@` at its centre. Figure A current of `10A` is flowing through it. Find the magnitude and direction of the magnetic field produced at the centre.
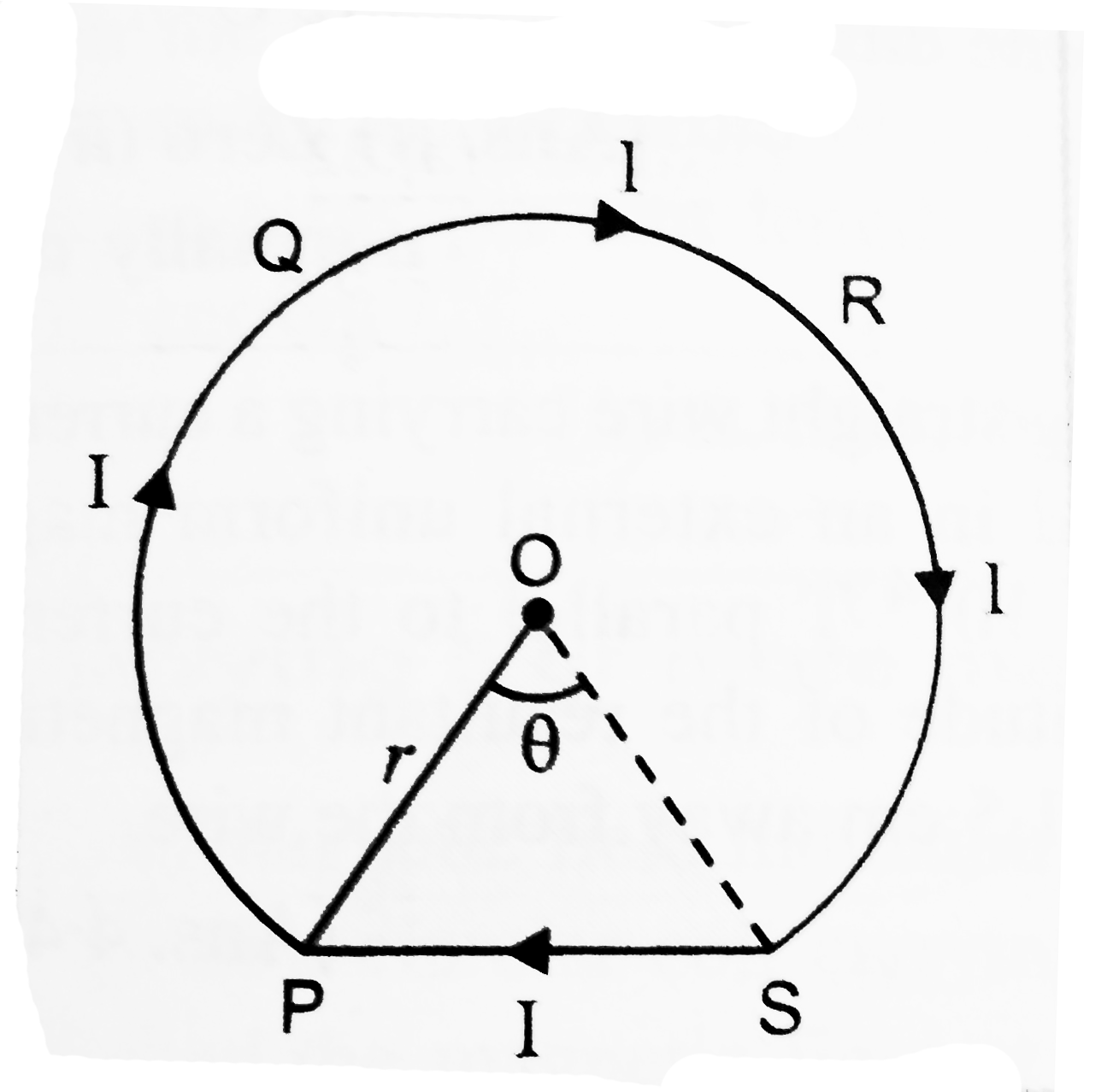
View SolutionA current `I(=4A)` flows along a thin wire PQRS shaped as shown in figure. The radius of the curved part of the wire is `10*0cm`. The angle `theta=90^@`. Find the magnitude of the total magnetic field at the point O.
View SolutionTwo identical coils each of radius `10cm` and having number of turns `100` are lying in perpendicular planes, such that they have common centre. Find the resultant magnetic field at the centre of the coils if they carry currents `3A` and `3sqrt3A` respectively.
View SolutionTwo identical loops P and Q each of radius `5cm` are lying in perpendicular planes such that they have a common centre as shown in the figure. Find the magnitude and direction of the net field at the common centre of the two coils, if they carry currents equal to `3A` and `4A` respectively.
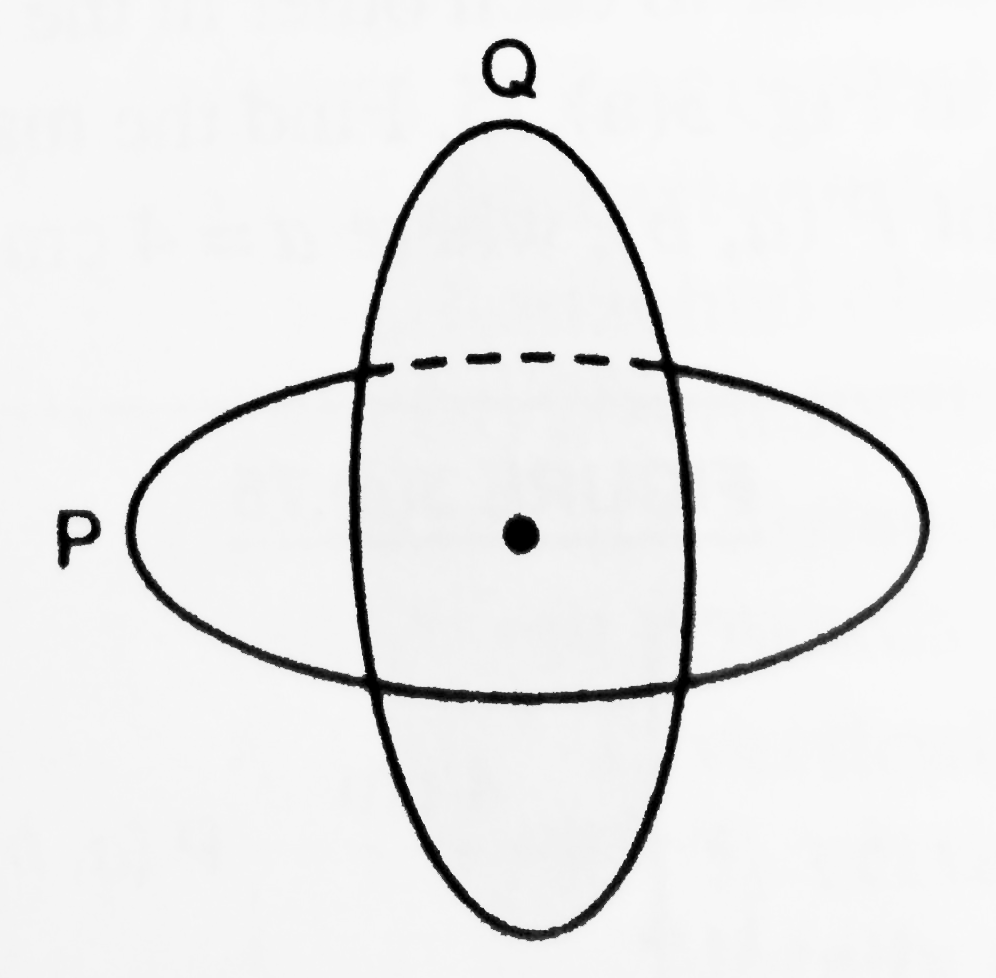
View SolutionTwo identical circular coils, P and Q, carrying currents `1A` and `sqrt3A` respectively, are placed concentrically and perpendicular to each other lying in the XY and YZ plane. Find the magnitude and direction of the net magnetic field at the centre of the coils.
View SolutionIn the net work shown in figure,find the magnetic field at the centre O of the coil.
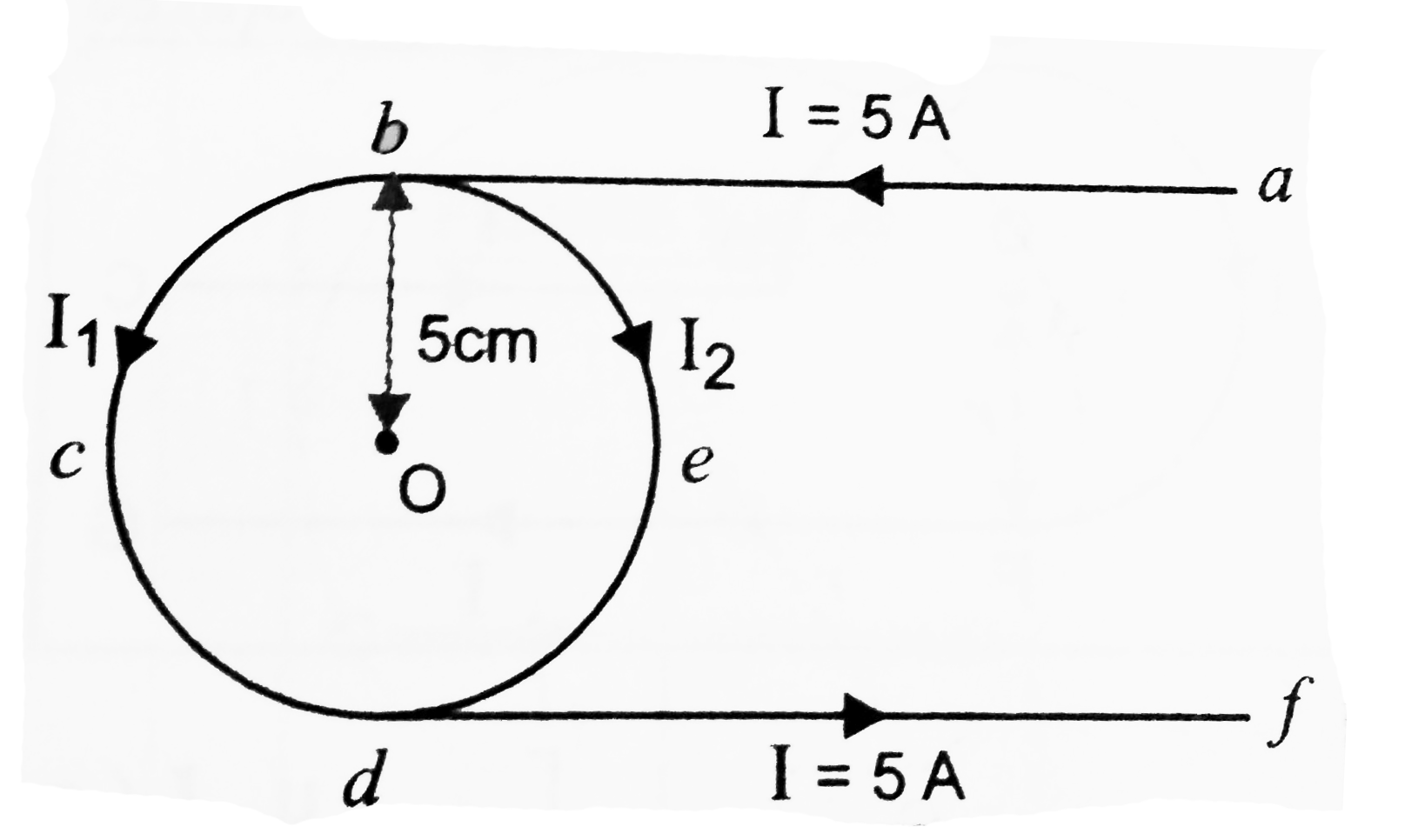
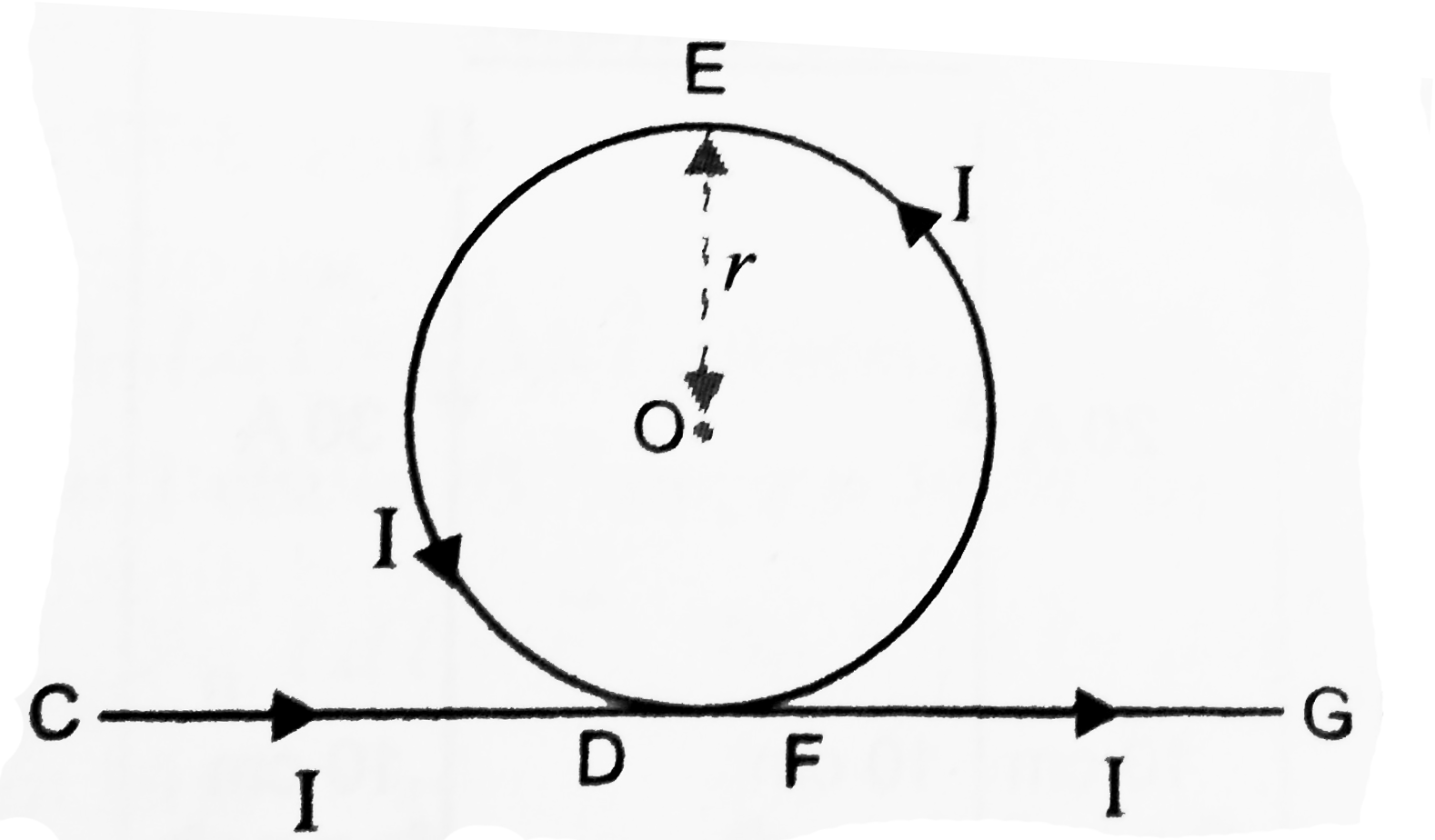
View SolutionAn electric current of I ampere is flowing in a long conductor CG as shown in figure. Find the magnitude and direction of magnetic induction at the centre O of circular part.
View SolutionA conductor carrying current I is of the type as shown in figure. Find the magnetic field induction at the common centre O of all the three arcs.

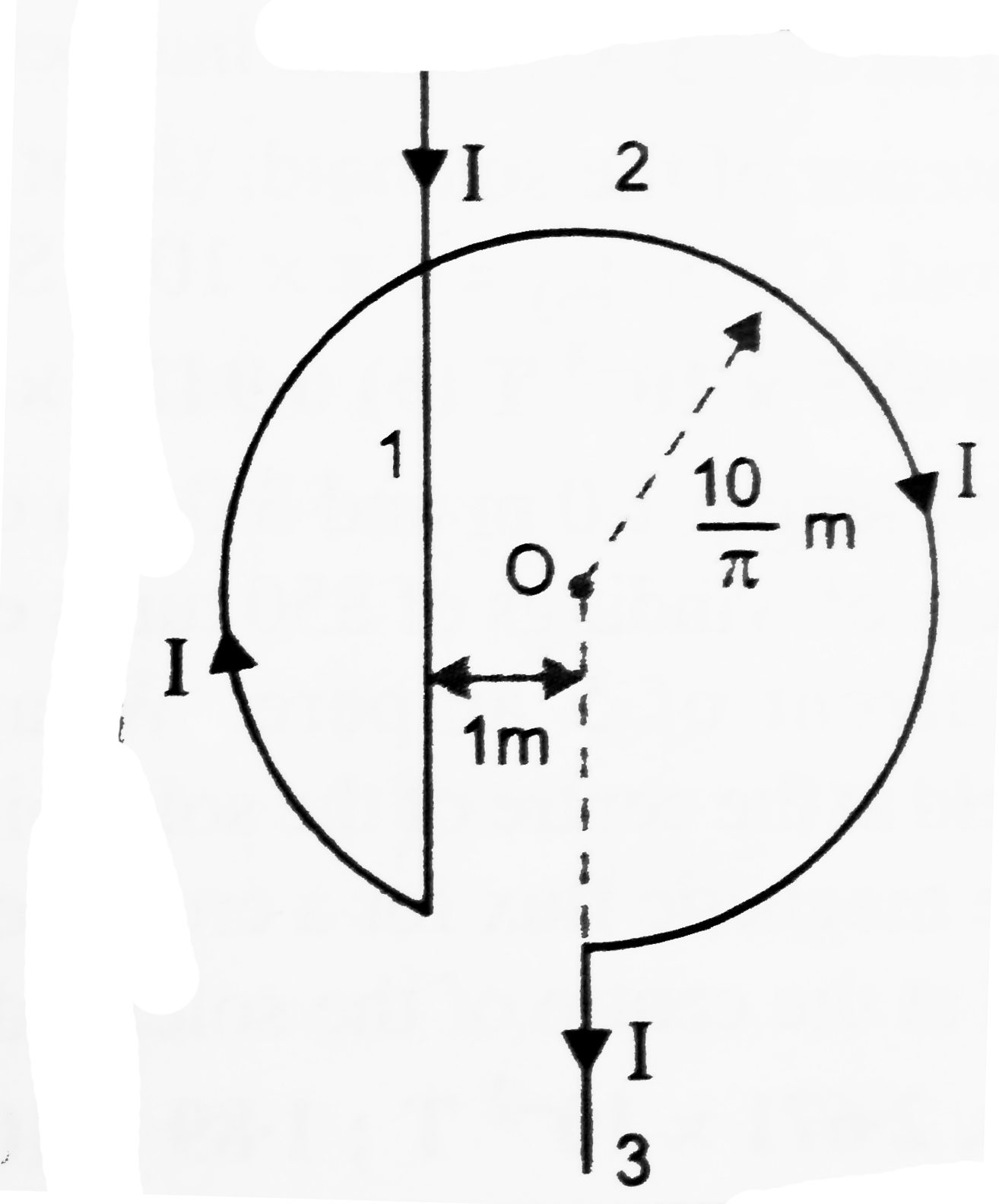
View SolutionA long straight wire carrying current I is bent into the shape as shown in the figure. The circular portion of the wire has radius `(10//pi)m`. The centre of this circle is at a distance `1m` from the straight portion of the wire. What is the magnitude of the magnetic field at the centre of the circular portion? Given `pi^2=10`.
View SolutionA long straight solid metal wire of radius R carries a current I, uniformly distributed over its circular cross-section. Find the magnetic field at a distance r from axis of wire (i) inside and (ii) outside the wire.
View SolutionA straight thick long wire of uniform cross-section of radius `5cm` is carrying a steady current `5A`. Calculate the magnetic field at a point `2cm` from the axis of wire, well inside the wire.
View SolutionA long straight solid conductor of radius `6cm` carries a current of `8A`, which uniformly distributed over its circular cross-section. Find the magnetic field (a) at a distance of `3cm` from the axis of the conductor (b) at a distance `10cm` from the axis of the conductor.
View SolutionIf the current density in a linear conductor of radius 'a' varies with r according to relation `J=kr^2`, where k is a constant and r is the distance of a point from the axis of conductor. Find the magnetic field induction at a point distance r from the axis, when (i) `rlta` and (ii) `rgta`.
View SolutionA `0.5m` long solenoid has `500` turns and has strength of magnetic field of `2.52xx10^-3T` at its center. Find the current in the solenoid.
View SolutionA solenoid of length `0*20m`, having `120` turns carries a current of `2*5A`. Find the magnetic field: (a) in the interior of the solenoid, (b) at one end of the solenoid. Given `mu_0=4pixx10^-7` S.I. units.
View SolutionA solenoid of length `1*0m` and `3*0cm` diameter has five layers of windings of `850` turns each hand carries a current of 5 ampere. What is the magnetic field at the centre of the solenoid? Also calculate the magnetic flux for a cross-section of the solenoid at the centre of the solenoid.
View SolutionA long wire carries a current of `20A` along the directed axis of a long solenoid. The field due to a solenoid is `4mT`. Find the resultant field at a point `3mm` from the solenoid axis.
View SolutionA copper wire having a resistance of `0*02Omega` per metre is used to wind a 500 turns solenoid of radius `2*0cm` and length `30cm`. What should be the `emf` of the battery which when connected across the solenoid would produce a magnetic field at `10^-2T`, near the centre of the solenoid.
View SolutionA coil wrapped around a toroid has inner radius of `10*0cm` and an outer radius of `20*0cm`. If the wire wrapped makes 600 turns and carries a current of `10*0A`, what are the maximum and minimum values of magnetic field within the toroid?
View Solution
Exercise questions and complete solutions for chapter MAGNETIC EFFECT OF CURRENT AND MAGNETISM of PRADEEP PHYSICS (HINGLISH) of Class 12
All Exercises from PRADEEP Class 12 PHYSICS MAGNETIC EFFECT OF CURRENT AND MAGNETISM
- Competition Focus (Multiple Choice Questions)
- Conceptual Problems (d)
- Exercise
- Fill in the blank (a)
- Fill in the blank (b)
- Fill in the blank (c)
- NCERT Exemplar Problems (Chapter 5 Short Answer Questions)
- Short Answer Questions (b)
- Solved Examples
- Test Your Grip (a)
- Test Your Grip (c)
- Test Your Grip (d)
- Value Based Questions
- Very Short Answer Questions (a)