Complete Solutions to PROBLEMS of chapter THE FIRST LAW OF THERMODYNAMICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | THE FIRST LAW OF THERMODYNAMICS |
| RESNICK AND HALLIDAY | PROBLEMS |
| Number Of Questions | 41 |
| Academic Year | 2023-24 |
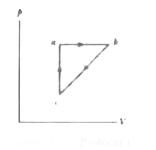
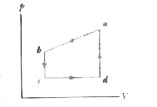
A lab sample of gas is taken through cyclic abca shown in the P-V diagram of fig 21-22 the net work done is + 1.5 J . Along paths Ab the change in the internal energy is +3.0 and the magnitude of the work done is 5.0 J Along path ca the energy transferred to the gas as heat is + 2.5 J . How much energy is transferred as heat along (a) path ab and (b) path bc ?
View SolutionWhen a system is taken from state I to state f along path iaf in fig - 21.23 Q = 100 cal and W = 40 cal Along path ibf Q = 72 cal . (a) what is W along path ibf ?
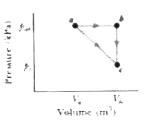
View SolutionThe themodynamic system is taken from state A to state B to state C , and then back from state A to p-V diagram of fig - 21.24 a . The vertical scale is set by `p_s = 20 `Pa and the table in fig . 21-24 by inserting a plus sign a minus sign or a zero in each indicated cell . (h ) what is the set work done by the system as it moves once through the cycle ABCA ?

View Solutionsuppose 200 J of work is done on a system and 80.0 cal is extracted from the system as heat . In the sence of the first law of thermodynamics what are the values ( including algbraic signs ) of (a) W ,(b ) Q m and (c ) `Delta E_(i n t) `?
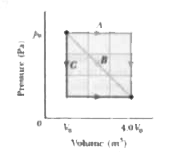
View SolutionIn fig - 21.25 a gas sample expands from `V_0 ` to `4.0 V_0 ` while its pressure decrease from `p_0 ` to `P_0 // 4.0` .if `V_0 = 1.0 m^3 ` and `p_0 = 60 Pa.` how much work is done by the gas if its pressure changes with volume via (a) path A . (b) path b, and (c ) path c ?
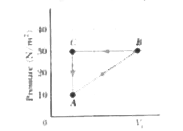
View SolutionA gas within a closed chamber undergoes the cycle shown in the p-V diagram of Fig. 21-26. The horizontal scale is set by `V_s = 8.0 m^3`. Calculate the net energy added to the system as heat during one complete cycle.
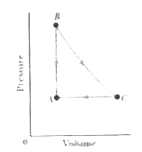
View SolutionAs a gas is held within a closed chamber, it passes through the cycle shown in Fig. 21-27 Determine the energy transferred by the system as heat during constant-pressure process CA if the energy added as heat `Q_(AB)` during constant-volume process AB is 25.0 J, no energy is transferred as heat during adiabatic process BC and the net work done during the cycle is 15.0 J.
View SolutionFigure 21-28 represents a closed cycle for a gas (the figure is not drawn to scale). The change in the internal energy of the gas as it moves from a to calong the path abc is -50 J. As it moves from c to d, 45 J must be transferred to it as heat. An additional transfer of 20 J to it as heat is needed as it moves from d to a. How much work is done on the gas as it moves from c to d?
View SolutionCalculate the specific heat of a metal from the following data. A container made of the metal has a mass of 3.6 kg and contains 15 kg of water. A 1.8 kg piece of the metal initially at a temperature of `180^@ C` is dropped into the water. The container and water initially have a temperature of `16.0^@ C`, and the final temperature of the entire (insulated) system is `18.0^@ C`.
View SolutionWhen 0.40 mol of oxygen (`O_2`) gas is heated at constant pressure starting at `0^@`C, how much energy must be added to the gas as heat to triple its volume? (The molecules rotate but do not oscillate.)
View SolutionA gas is to be expanded from initial state i to final state f along either path 1 or path 2 on a p-V diagram. Path 1 consists of three steps: an isothermal expansion (work is 23 J in magnitude), an adiabatic expansion (work is 35 J in magnitude), and another isothermal expansion (work is 16 J in magnitude). Path 2 consists of two steps: a pressure reduction at constant volume and an expansion at constant pressure . what is the change in the internal energy of gas along path 2 ?
View SolutionWhen 22.5 J was added as heat to a particular ideal gas, the volume of the gas changed from 50.0 `cm^3` to 100 `cm^3` while the pressure remained at 1.00 atm. (a) By how much did the internal energy of the gas change? If the quantity of gas present was `2.00 xx 10^(-3)`mol, find (b)`C_p` and (c) `C_v`
View SolutionSuppose 2.80 mol of an ideal diatomic gas, with molecular rotation but not oscillation, experienced a temperature increase of 45,0 K under constant-pressure conditions. What are (a) the energy transferred as heat , (b) the change `Delta E_( i n t)` internal energy of the gas, (c) the work w done by the gas, and (d) the change `Delta `K in the total translational kinetic energy of the gas?
View SolutionThe temperature of 4.50 mol of an ideal monatomic gas is raised 27.0 K at constant volume. What are (a) the work W done by the gas, (b) the energy transferred as heat Q. (c) the change `Delta E_( i n t) ` in the internal energy of the gas, and (d) the change `Delta `K in the average kinetic energy per atom?
View SolutionOpening champagne. In a bottle of champagne, the pocket of gas (primarily carbon dioxide) between the liquid and the cork is al pressure of `p_i` = 4.00 atm. When the cork is pulled from the bottle, the gas undergoes an adiabatic expansion until its pressure matches the ambient air pressure of 1.00 atm. Assume that the ratio of the molar specific heats is `gamma`= 4/3. If the gas has initial temperature `T=5.00^@ C`, what is its temperature at the end of the adiabatic expansion?
View SolutionOne mole of an ideal diatomic gas goes from a to c along the diagonal path in Fig. 21-29. The scale of the vertical axis is set by `P_(ab)= 5.0 kPa and p_c = 0.50 kPa,` and the scale of the horizontal axis is set by `V_a = 2.0 m^3 ` During the transition, (a) what is the change in internal energy of the gas, and (b) how much energy is added to the gas as heat? (c) How much heat is required if the gas goes from a to c along the indirect path abc?
View SolutionAdiabatic wind. The normal airflow over the Rocky Mountains is west to east. The air loses much of its moisture content and is chilled as it climbs the western side of the mountains. When it descends on the eastern side, the increase in pressure toward lower altitudes causes the temperature to increase. The flow, then called a chinook wind, can rapidly raise the air temperature at the base of the mountains. Assume that the air pressure p depends on altitude y according to `p = P_0 ` exp (-ay), where `P_0 = 1.00` atm and a =` 1.16 xx 10^(-4) `m. Also assume that the ratio of the molar specific heats is `gamma`= 4/3. A parcel of air with an initial temperature of `-13.0^@ `C descends adiabatically from `Y_1 = 4267 `m to y = 1567 m. What is its temperature at the end of the descent?
View SolutionWe give 90 J as heat to a diatomic gas, which then expands at constant pressure. The gas molecules rotate but do not oscillate. By how much does the internal energy of the gas increase?
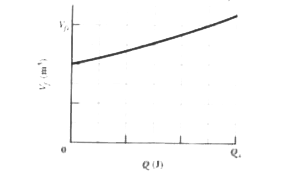
View SolutionSuppose 0.825 mol of an ideal gas undergoes an isothermal expansion as energy is added to it as heat Q. If Fig. 21-30 shows the final volume `V_f` versus Q, what is the gas temperature? The scale of the vertical axis is set by `V_(fs ) = 0.30 m^3 ` and the scale of the horizontal axis is set by `Q_s = 1800 J`.
View SolutionFigure 21-31 shows a cycle undergone by 2.00 mol of an ideal monatomic gas. 2. The temperatures are `T_1 = 300 K, T_2 =600 K, and T_3 = 455 K.` For 1`to ` 2, what are (a) heat Q, (b) the change in internal energy `Delta E _(i nt )`, . and (c) the work done W? For `2 to 3`. what are (d) Q. (e) `Delta E_(i n t)`, and (f) W? For `3 to 1`, what are (g) (h) `Delta E_( i n t)`, and (i) W? For the full cycle, what are (j)(k) `Delta E_( i n t) `, and (1) W? The initial pressure at point 1 is 1.00 atm (= 1.013 10% Pa). What are the (m) volume and (n) pressure at point 2 and the (o) volume and (p) pressure at point 3?
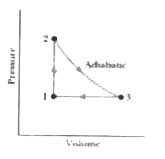
View SolutionAn ideal diatomic gas, with rotation but no oscillation,undergoes an adiabatic compression. Its initial pressure and volume are 1.20 atm and 0.200 m . Its final pressure is 3.60 atm. How much work is done by the gas?
View SolutionThe volume of an ideal gas is adiabatically reduced from 350 L to 130 L. The initial pressure and temperature are 2.00 atm and 380 K. The final pressure is 8.00 atm. (a) is the gas monatomic, diatomic, or polyatomic? (b) What is the final temperature? (c) How many moles are in the gas?
View SolutionUnder constant pressure, the temperature of 3.00 mol of an ideal monatomic gas is raised 15.0 K. What are (a) the work W done by the gas, (b) the energy transferred as heat Q. (c) the change `Delta E _( i n t )` in the internal energy of the gas, and (d) the change `Delta `K in the average kinetic energy per atom?
View SolutionAn automobile tire has a volume of `1.64 xx 10^2 m^3` and contains air at a gauge pressure (pressure above atmospheric pressure) of 165 kPa when the temperature is 0.00°C. What is the gauge pressure of the air in the tires when its temperature rises to 37.0°C and its volume increases to `1.67 xx 10^(-2)m^4` Assume atmospheric pressure is `1.01 xx 10^5 ` Pa.
View SolutionSuppose 1.00 L of a gas with `gamma`= 1.30, initially at 285 K and 1.00 atm, is suddenly compressed adiabatically to half its initial volume. Find its final (a) pressure and (b) temperature. (C) If the gas is then cooled to 273 K at constant pressure, what is its final volume?
View SolutionA certain gas occupies a volume of 0.76 L at a pressure of 1.2 atm and a temperature of 4000 K. It is expanded adiabatically to a volume of 4.3 L. Determine (a) the final pressure and (b) the final temperature, assuming the gas to be an ideal gas for which `gamma` = 1.4.
View SolutionThe mass of a gas molecule can be computed from its specific heat at constant volume `c_V `. (Note that this is not `C_V `) Take `c_v = 0.1476 cal//g^@ C` for neon and calculate (a) the mass of a neon atom and (b) the molar mass of neon.
View SolutionAir that initially occupies 0.280 m at a gauge pressure of 103.0 kPa is expanded isothermally to a pressure of 101.3 kPa and then cooled at constant pressure until it reaches its initial volume. It then returns to its initial pressure in a constant-volume process. Compute the network done by the air. (Gauge pressure is the difference between the actual pressure and atmospheric pressure.)
View SolutionA sample of an ideal gas is taken through the cyclic process abca shown in Fig.21-33. The scale of the vertical axis is set by `p_b = 7.5 kPa `and` p_(Ac ) = 2.5 kPa. `At point a, T = 280 K. (a) How many moles of gas are in the sample? What are (b) the temperature of the gas at point b, (c) the temperature of the gas at point c, and (d) the Higure 21-33 Problem 30. net work done by the gas during the cycle, and (c) the net energy added to the gas as heat during the cycle?
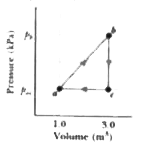
View SolutionSuppose 1.80 mol of an ideal gas is taken from a volume of 3,00 `m^3 ` to a volume of `5.50 m^3` via an isothermal expansion at `30^@ C`. (a) How much energy is transferred as heat during the process, and (b) is the transfer to or from the gas?
View SolutionA Carnot engine has an efficiency of 15.0%. It operates between constant temperature reservoirs differing in temperature by 55.0°C What is the temperature of the lower-temperature reservoir?
View SolutionFigure 21-34 shows a reversible cycle through which 1.00 mol of a monatomic ideal gas is taken. Assume that `p = 2p_0 V = 2V_0 , P_0 = 1.01 xx 10^5` Pa, and `V_0 = 0.0335 m^3`. Calculate (a) the work done during the cycle, (b) the energy added as heat during stroke Volume abc, and (c) the efficiency of the cycle. (d) What is the efficiency of a Carnot engine operating between the highest and lowest temperatures that occur in the cycle?
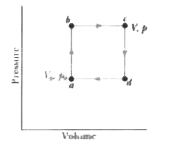
View SolutionA Carnot engine whose high-temperature reservoir is at 483 K has an efficiency of 40%. By how much should the temperature of the low-temperature reservoir be decreased to increase the efficiency to 50%?
View SolutionIn a hypothetical nuclear fusion reactor, the fuel is deuterium gas at a temperature of` 7 xx 10^8` K. If this gas could be used to operate a Carnot engine with `T_L = 50^@ C`, what would be the engine's efficiency? Take both temperatures to be exact and report your answer to eight significant figures.
View SolutionAn ideal gas (3.0 mol) is the working substance in an engine that operates on the cycle shown in Fig. 21-35. Processes BC and DA are reversible and adiabatic. (a) Is the gas monatomic, diatomic, or polyatomic? (b) What is the engine efficiency?
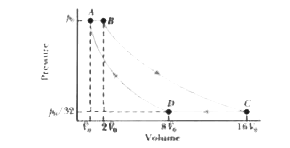
View Solution(a) During each cycle, a Carnot engine absorbs 730 J as heat from a high-temperature reservoir at 360 K, with the low-temperature reservoir at 280 K. How much work is done per cycle? (b) The engine is then made to work in reverse to function as a Carnot refrigerator between those same two reservoirs. During each cycle, how much work is required to remove 1200 J as heat from the low-temperature reservoir?
View Solution(a) For 2.5 mol of a monatomic ideal gas taken through the cycle in Fig. 21-36, where `V_1 - 4.00V_0 `, what is `W//p_0 V_0 ` as the gas goes from state a to state c along path abc?
View SolutionA 600 W Carnot engine operates between constant temperature reservoirs at `100^@ `C and `60.0^@ C`. What is the rate at which energy is (a) taken in by the engine as heat and (b) exhausted by the engine as heat?
View SolutionA Carnot engine is set up to produce a certain work W per cycle. In each cycle, energy in the form of heat `Q_H `is transferred to the working substance of the engine from the higher-temperature thermal reservoir, which is at an adjustable temperature `T_H`. The lower-temperature thermal reservoir is maintained at temperature `T_L = 250 K.` Figure 21-37 gives `Q_H `for a range of `T_H ` The scale of the vertical axis is set by `Q_Hs ` = 12.0 kJ. If `T_H ` is set at 550 K, what is `Q_H `?
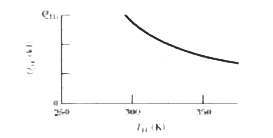
View SolutionFigure 21-38 shows a reversible cycle through which 1.00 mol of a monatomic ideal gas is taken. Volume `V_C ` = 8.00 `V_b ` Process Adiabatic bc is an adiabatic expansion, with `p_b = 5.00` atm and `V_b = 1.00 xx 10^(-3) m^3 `. For the cycle, find (a) the energy added to the gas as heat, (b) the energy leaving the gas as Volume heat, (c) the network done by the gas, and (d) the efficiency of the cycle.
View SolutionA Carnot engine operates between `235^@ C and 115^@ C,` absorbing `3.00 xx 10^4` J per cycle at the higher temperature. (a) How much energy per cycle is discharged at the lower temperature? (b) How much work per cycle is this engine capable of performing?
View Solution
PROBLEMS questions and complete solutions for chapter THE FIRST LAW OF THERMODYNAMICS of RESNICK AND HALLIDAY PHYSICS (HINGLISH) of Class 12