Complete Solutions to Problems of chapter MAGNETIC FIELDS DUE TO CURRENTS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MAGNETIC FIELDS DUE TO CURRENTS |
| RESNICK AND HALLIDAY | Problems |
| Number Of Questions | 45 |
| Academic Year | 2023-24 |
In Fig. `29-40` point P, is at distance `R=24.0` cm on the perpendicular bisector of a straight wire of length `L=18.0`cm carrying current `i=58.2` mA. (Note that the wire is not long). What are the (a) magnitude and (b) direction of the magnetic field at `P`, due to i ? (c ) If R is increased, what happens to the magnitude of the field ?
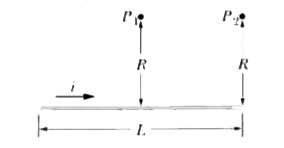
View SolutionIn Fig `29-40` point `P_(2)` is at perpendicular distance `R=25.1` cm from one end of a straight wire of length `L=13.6` cm carrying current `i=0.500` A. (Note that the wire is not long ) (a) What is the magnitude of the magnetic field at `P_(2)` ? (b) If the point of measurement is moved from `P_(2)` to `P_(1)` does the field magnitude increase, decrease, or remain the same ?
View SolutionFour very long wires are arranged as shown in the figure, so that their cross - section forms a square, with connections at the ends so that current I flow through all four wires. Length of each side of the formed such square is b. The magnetic field at the central point P (centre of the square) is
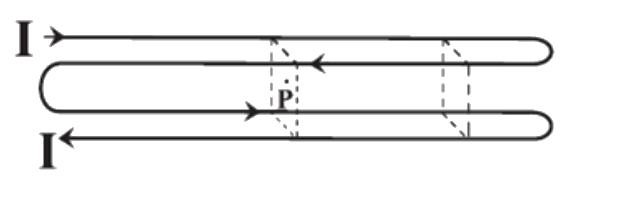
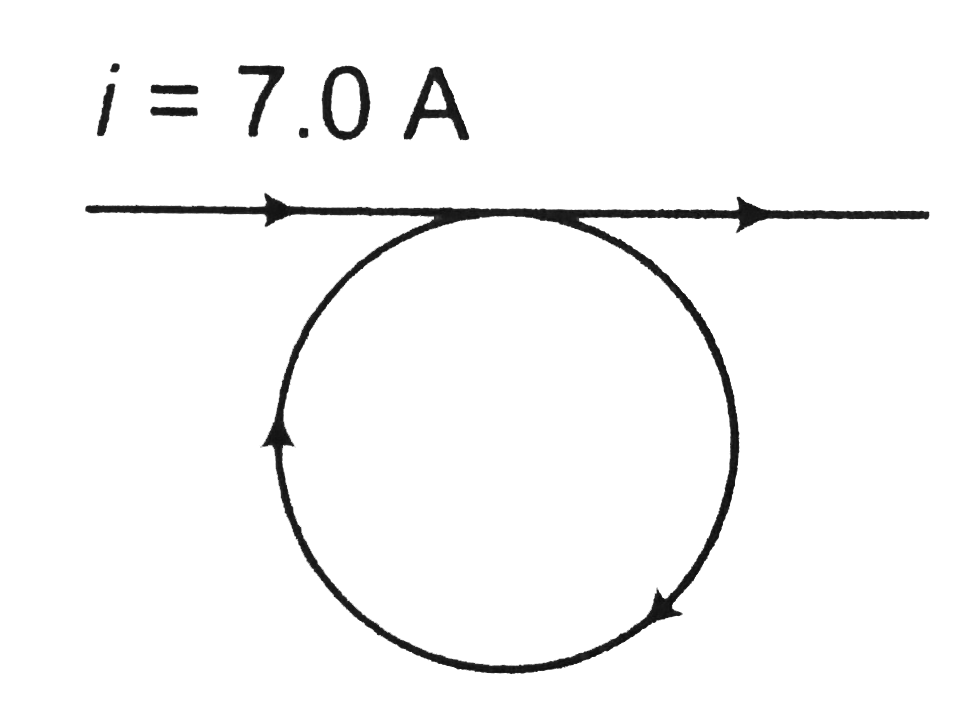
View SolutionA conductor consists of a circular loop of radius `R =10 cm` and two straight, long sections as shown in figure. The wire lies in the plane of the paper and carries a current of `i = 7.00 A` Determine the magnitude and direction of the magnetic field at the centre of the loop.
View SolutionIn Fig. `29-41` four long straight wires are perpendicular to the page, and their cross sections form a square of edge length `a=13.5` cm. Each wire carries `7.50` A, and the currents are out of the page in wires `1,3,` and `4` and into the page in wire `2`. In unit - vector notation, what is the net magnetic force per meter of wire length on wire `4` ?
View SolutionIn Fig. `29-41` four long straight wires are perpendicular to the page, and their cross sections form a square of edge length `a=8.50` cm. Each wire carries `15.0` A, and all the currents are out of the page. In unit - vector notation, what is the net magnetic force per meter of wire length on wire `1` ?
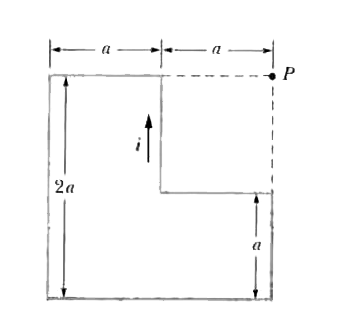
View SolutionIn Fig. `29-43,` length a is `2.3` cm (short) and current i is `18` A. What are (a) magnitude and (b) direction ( into or out of the page ) of the magnetic field at point P ?
View SolutionTwo long parallel wires are separated by a distance of `2.50 cm`. The force per unit length that each wire exerts on the other is `4.00xx10^-5 N/m`, and the wires repel each other. The current in one wire is `0.600A`.
a. What is the current in the second wire ?
b. Are the two currents in the same direction or in opposite direction?
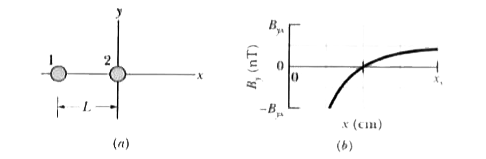
View SolutionFigure `29-45` a shows, in cross section, two long, parallel wires carrying current and separated by distance L. The ratio `i_(1)//i_(2)` of their currents is `4.00,` the directions of the currents are not indicated. Figure `29-45b` shows the y component `B_(y)` of their net magnetic field along the x axis to the right of wire `2`. The vertical scale is set by `B_(ys)=4.0` nT, and the horizontal scale is set by `x_(s)=20.0` cm. (a) At what value of `xgt0` is `B_(y)` maximum ? (b) If `i_(2)=3` mA, What is the value of that maximum ? What is the direction ( into or out of the page ) of (c ) `i_(1)` and (d) `i_(2)` ?
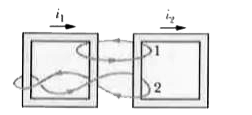
View SolutionFigure `29-46` shows two closed paths wrapped around two conducting loops carrying currents `i_(1)=5.0` A and `i_(2)=3.0` A What is the value of the integral `ointvecB.dvecs` for (a) path `1` and (b) path `2` ?
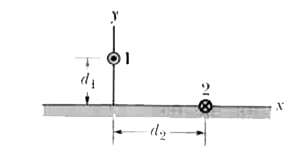
View SolutionFigure `29-47` shows wire `1` in cross section, the wire is long and straight, carries a current of `2.50` mA out of the page, and is at distance `d_(1)=4.00` cm from a surface. Wire `2`, which is parallel to wire `1` and also long, is at horizontal distance `d_(2)=5.00` cm wire `1` and carries a current of `6.80` mA into the page. What is the x component of the magnetic force per unit length on wire `2` due to wire `1` ?
View SolutionAn electron is shot into one end of a solenoid.As it enters the uniform magnetic field within the solenoid, its speed is `800 m//s` and its velocity vector makes an angle of `30^(@)` with the central axis of the solenoid.The solenoid carries `4.0 A` current and has `8000` turn along its length.Find number of revolutions made by the electron within the solenoid by the time it emerges from the solenoid's opposite end. (Use charge of mass ratio `e/m` for electron `=sqrt3xx10^(11) C//kg`)Fill your answer in multiple of `10^(3)` (neglect end effect)
View SolutionA toroid with mean radius `r_(0)`, diameter `2a` have N turns carrying current l. What is the magnetic field B inside the the toroid?
View SolutionFigure shows a cross-section of a long ribbon of width `omega` that is carrying a uniformly distributed total current i into the page. Calculate the magnitude and direction of the magnetic field `B` at a point `P` in the plane of the ribbon at a distance d from its edge. `

View SolutionFigure shows a cross-section of a long ribbon of width `omega` that is carrying a uniformly distributed total current i into the page. Calculate the magnitude and direction of the magnetic field `B` at a point `P` in the plane of the ribbon at a distance d from its edge. `

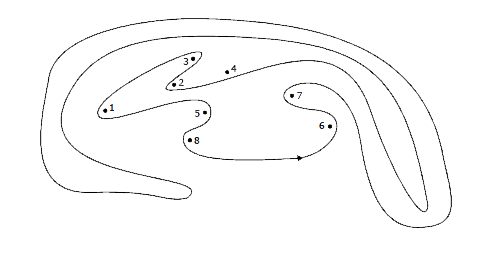
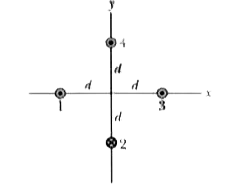
View SolutionEight wires cut the page perpendicularly at the points show in figure. A wire labeled with the integer k `(k=1.2,…….8)` bears the current `ki_(0)`. For those with odd k, the current flows up out of the page, for those with even k it flows down into the page. The value of `ointvecB.dvecr` along the close path (as shown in the figure) in the direction indicated by the arrow is
View SolutionA current of `1//(4pi)` ampere is flowing in a long straight conductor. The line integral of magnetic induction around a closed path enclosing the current carrying conductor is
View SolutionA long solenoid with 10 turn / cm and a radius of 7.0 cm carries a current of 20.0 mA .A current of 6.0 A exists in a straight conductor loacted along the central axis of the solenoid at what radial distance from the axis will the direction of the magneitic field be at `45^(@)` to the axial direction
View SolutionTwo wire loop PQRSP formed by joining two semicircular wires of radii `R_(1) and R_(2)` carries a current i as shown in the figure given below. What is the magnetic field induction at the centre O in cases (A) and (B) ?
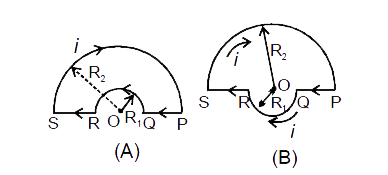
View SolutionA `470` - turn solenoid having a length of 25 cm and a diameter of 10 cm carries a current of `0.29`A. Calculate the magnitude of the magnetic field `vecB` inside the solenoid.
View SolutionWhat is magnetic dipole moment? Calculate the magnetic dipole moment of a revolving electron.
View SolutionFigure shows a straight wire of length a carrying a current `I`. What is the magnitude of magnetic field induction produced by the current at P, which is lying at a perpendicular distance a from one end of the wire.


View SolutionA long solenoid has 200 turns per cm and carries a current of 2.5A. The magnetic field at its centre is
View SolutionThe current density `bar(J)` inside a long, solid cylindrical wire of radius `a = 12 mm` is in the direction of the central axis, and its magnitude varies linearly with radial distance r from the axis according to `J = (J_(0) r)/(a)`, where `J_(0) = (10^(5))/(4 pi) A//m^(2)`. Find the magnitude of the magnetic field at `r = (a)/(2)` in `mu T`
View SolutionA circular loop of radius `12` cm carries a current of `7.2` A. A flat coil of radius `0.82` cm, having `50` turns and a current of `1.3` A, is concentric with the loop. The plane of the loop is perpendicular to the plane of the coil. Assume the loop's magnetic field is uniform across the coil. What is the magnitude of (a) the magnetic field produced by the loop at its centre and (b) the torque on the coil due to the loop ?
View SolutionAt a place, the horizontal component of earth's magnetic field is B and angle of dip is `60^@`. What is the value of horizontal component of earth's magnetic field at equator?
View SolutionA student makes a short electromagnet by winding `280` turns of wire around a wooden cylinder of diameter `d=5.0` cm. The coil is connected to a battery producing a current of `3.8` A in the wire. (a) What is the magnitude of the magnetic dipole moment of this device ? (b) At what axial distance `zgtgt` d will the magnetic field have the magnitude `5.0mu` T (approximately one - tenth that of Earth's magnetic field ) ?
View SolutionIn Fig `29-54,` two long straight wires are perpendicular to the page and separated by distance `d_(1)=0.75` cm. Wire `1` carries `6.5` A into the page. What are the (a) magnitude and (b) direction (into or out of the page ) of the current in wire `2` if the net magnetic field due to the two currents is zero at point P located at distance `d_(2)=2.50` cm from wire `2` ? If the current in wire `2` is then reversed, what are the (c ) size and (d) direction of the net field at point P ?
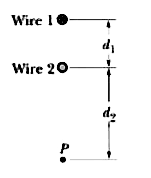
View SolutionA conductor consists of a circular loop of radius `R =10 cm` and two straight, long sections as shown in figure. The wire lies in the plane of the paper and carries a current of `i = 7.00 A` Determine the magnitude and direction of the magnetic field at the centre of the loop.

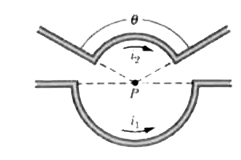
View SolutionFigure `29-56` shows two current segments. The lower segment carries a current of `i_(1)=0.40` A and includes a semicircular are with radius `5.0` cm, angle `180^(@)` and center point P. The upper segment carries current `i_(2)=3i_(1)` and includes a circular are with radius `4.0` cm, angle `120^(@)` and the same centre point P. What are the (a) magnitude and (b) diretion of the net magnetic field `vecB` at P for the indicated current directions ? What are the (c ) magnitude and (d) direction of `vecB` if `i_(1)` is reversed ?
View SolutionIn Fig. `29-57,` two long straight wires ( shown in cross section ) carry the currents `i_(1)=30.0` mA and `i_(2)=50.0` mA directly out of the page. They are equal distances from the origin, where they set up a ,magnetic field `vecB`. To what value must current `i_(1)` be changed in order to rotate `vecB25^(@)` clockwise ?
View SolutionA long straight wire AB carries a current of 4 A. A proton P travels at `4xx10^(6) ms^(-1)` parallel to the wire 0.2 m from it and in a direction opposite to the current as shown in the figure. Calculate the force which the magnetic field due to the current carrying wire exerts on the proton. Also specify its direction.
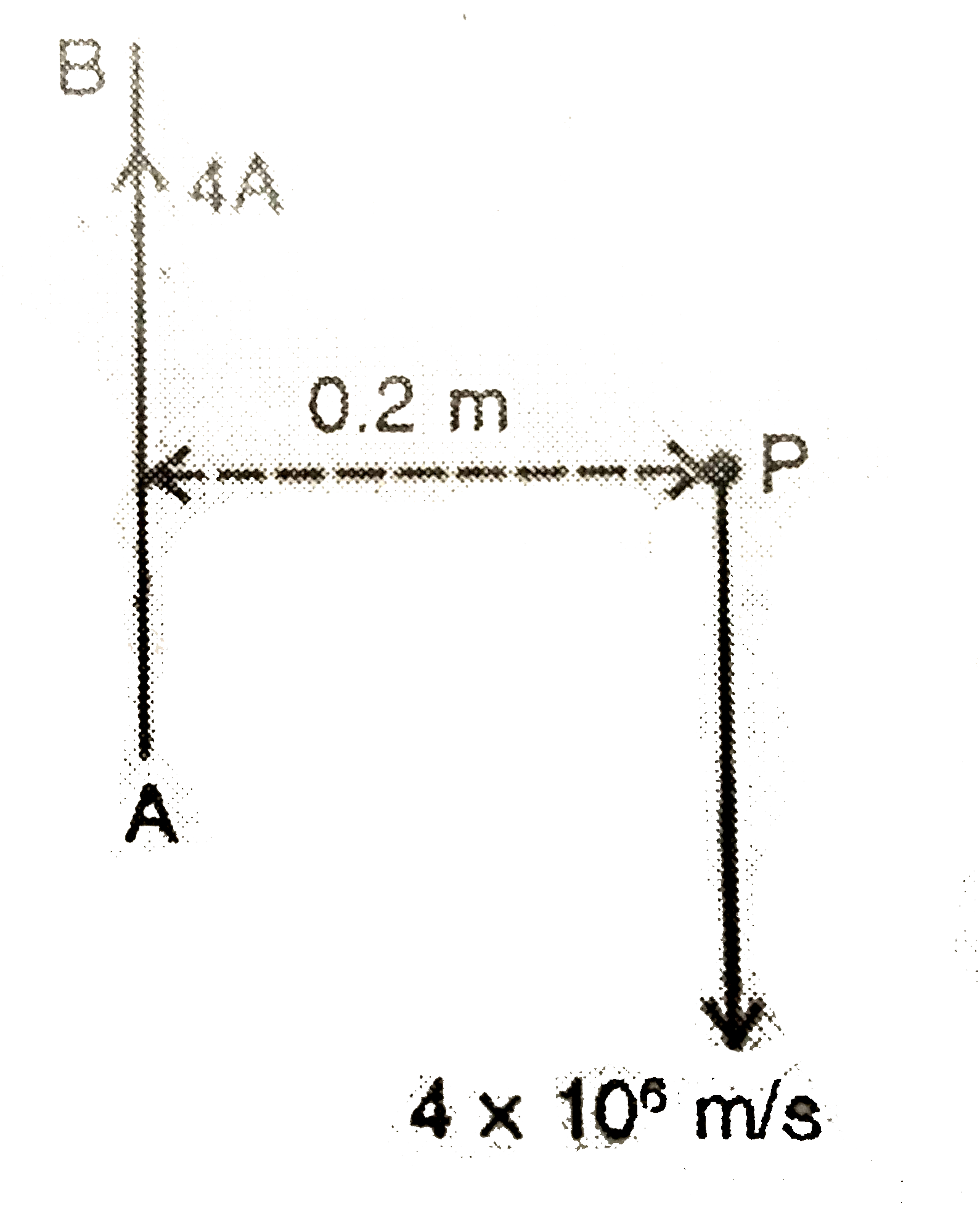
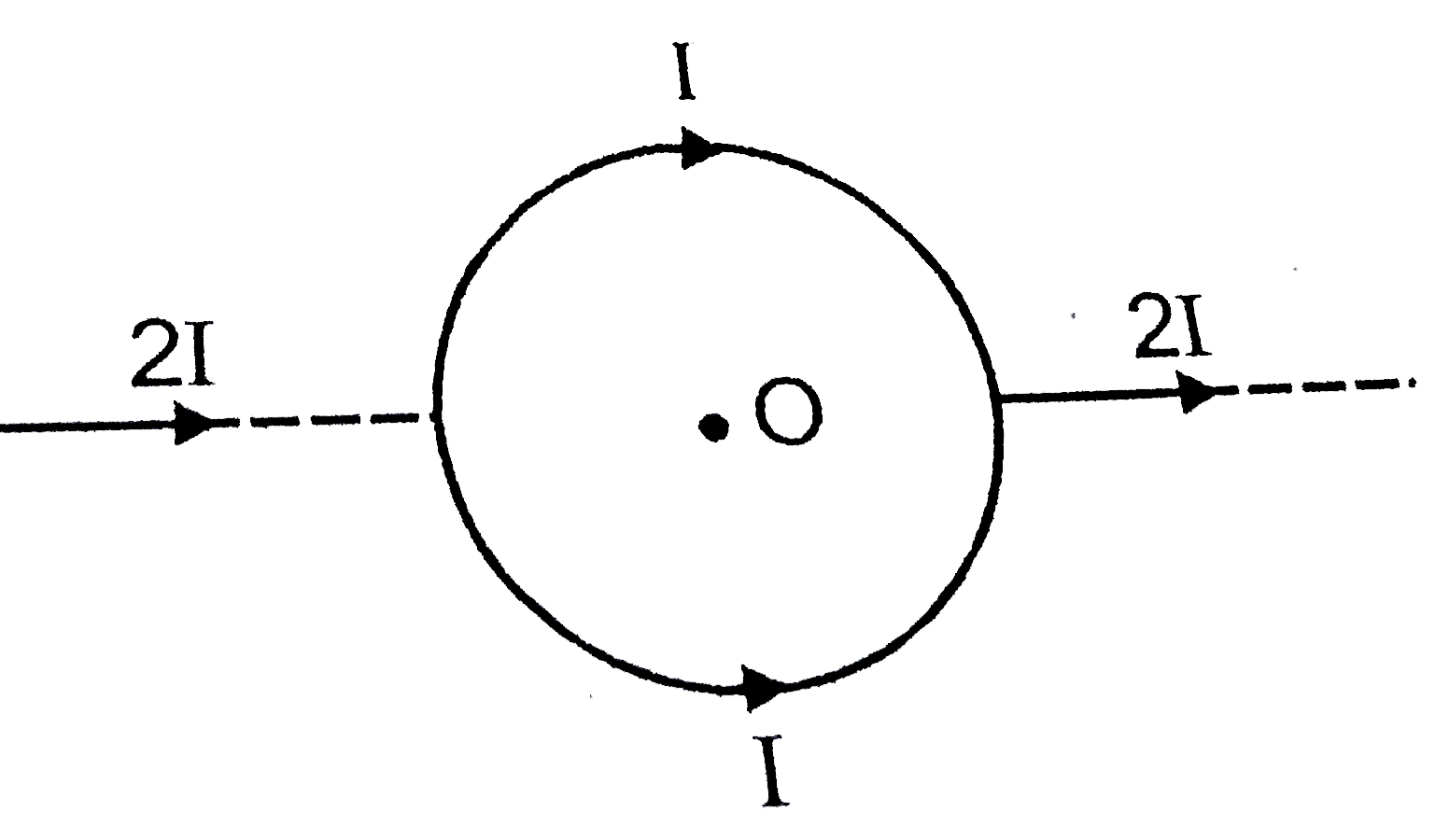
View SolutionAn infinite straigh conductor carrying current 2 I is split into a loop of radius r as shown in fig. the magnetic field at the centre of the coil is
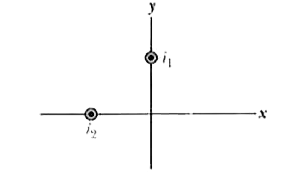
View SolutionA long wire is along `x = 0, z = d` and carries current in positive y direction. Another wire is along `x = y, z = 0` and carries current in direction making acute angle with positive x direction. Both the wires have current I. Find the magnitude of magnetic induction at `(0, 0, 2d)`.
View SolutionTwo identical coaxial circular loops carry a current `i` each circulating int the same direction. If the loops approch each other the current in
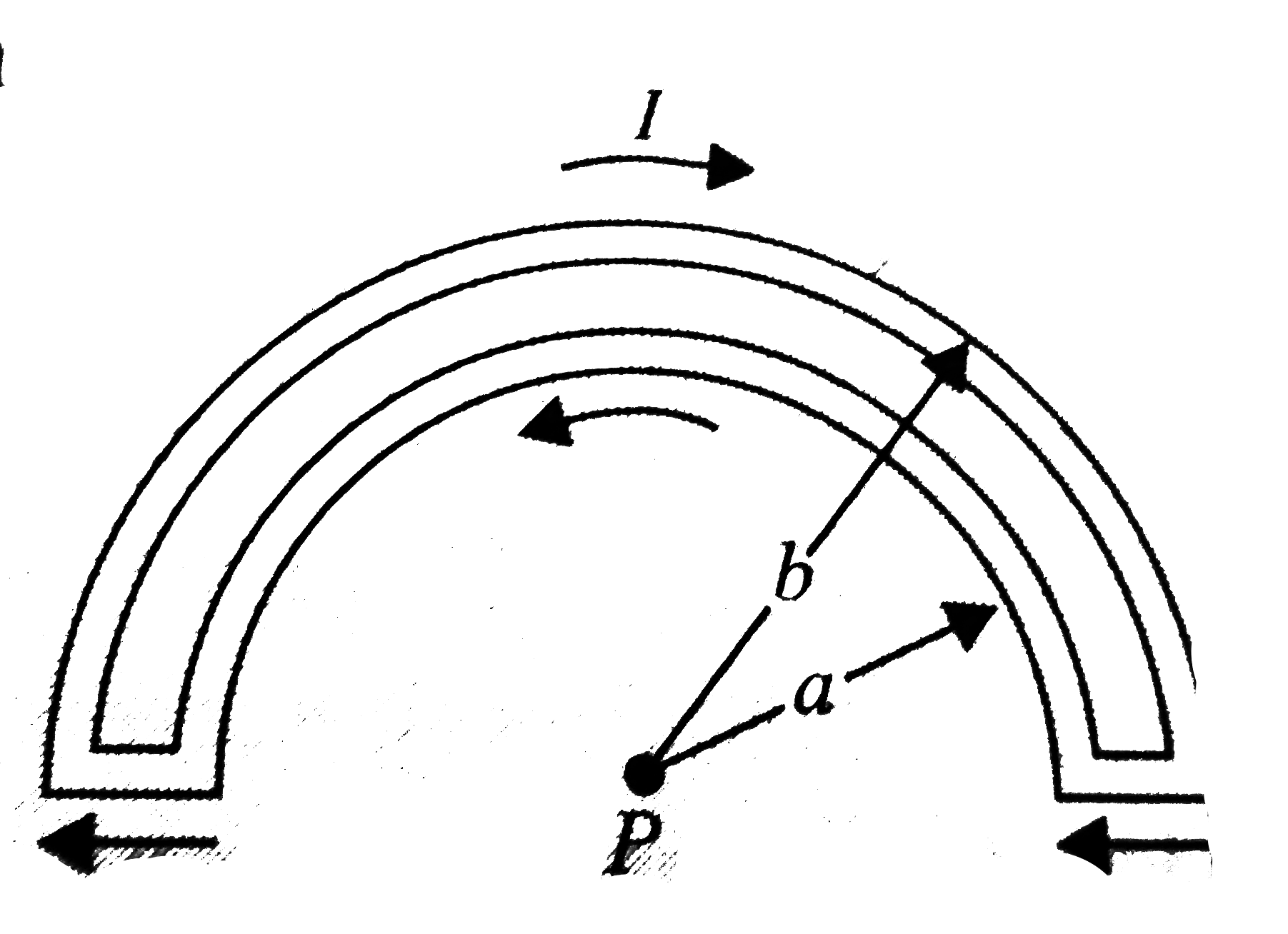
View SolutionTwo semicircles shown in Fig. have radii a and b. Calculate the net magnetic field (magnitude and direction) that the current in the wires produces at point P.
View SolutionTwo straight infinitely long and thin parallel wires are spaced 0.1m apart and carry a current of 10A each. Find the magnetic field at a point distance 0.1m from both wires in the two cases when the currents are in the (a) same and (b) opposite directions.
View SolutionFigure` 29-62` shows, in cross section, four thin wires that are parallel, straight, and very long. They carry identical currents in the directions indicated. Initially all four wires are at distance `d=15.0` cm from the origin of the coordinate system, where they create a net magnetic field `vecB`.
(a) To what value of `x` must you move wire`1`along the `x` axis in order to rotate`vecB` counterclockwise by `30^(@)`?
(b) With wire `1` in that new position, to what value of `x`must you move wire `3` along the `x` axis to rotate `vecB` by `30^(@)` back to its initial orientation ?
View SolutionFind the intensity of gravitational field at a point lying at a distance `x` from the centre on the axis of a ring of radius `a` and mass `M`.
View SolutionHow are the magnitude and direction of magnetic field at a point denoted by the magnetic lines of force ?
View SolutionIn a homogeneous magnetic field B there is an electron moving in a circular orbit with a speed v. Find the ratio of the magnetic field generated by the moving electron at the middle of the circle and the magnetic field making it revolve.
View SolutionTwo circular coils X and Y, having equal number of turns and carrying currents in the same sense, subtend same solid angle at point O. If the smaller coil X is midway between O and Y and if we represent the magnetic induction due to bigger coil Y at O as `B_y` and the due to smaller coil X at O as `B_x`,then find the ratio `B_x//B_y`.

View SolutionTwo protons move parallel to each other with an equal velocity `v=300kms^-1`. Find the ratio of forces of magnetic and electric interaction of the protons.
View SolutionA long solenoid is fabricated by closely winding a wire of radius 0.5 mm over a cylindrical nonmagnetic frame so that the successive turns nearly touch each other. What would be the magnetic field B at the centre of the solenoid if it carries a current of 5 A?
View SolutionFigure `29-64` shows a cross section of a long cylindrical conductor of radius `a=4.00` cm containing a long cylindrical hole of radius `b=1.50` cm. The central axes of the cylinder and hole are parallel and are distance `d=2.00` cm apart, current `i=5.25` A is uniformly distributed over the tinted area. (a) What is the magnitude of the magnetic field at the centre of the hole ? (b) Discuss the two special cases `b=0` and `d=0.`
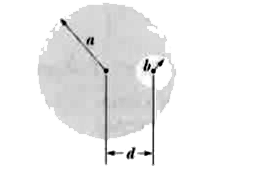
View Solution
Problems questions and complete solutions for chapter MAGNETIC FIELDS DUE TO CURRENTS of RESNICK AND HALLIDAY PHYSICS (HINGLISH) of Class 12