Complete Solutions to SAMPLE PROBLEMS of chapter ELECTROMAGNETIC INDUCTION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTROMAGNETIC INDUCTION |
| RESNICK AND HALLIDAY | SAMPLE PROBLEMS |
| Number Of Questions | 14 |
| Academic Year | 2023-24 |
A current l = 1.5 A is flowing through a long solenoid of diameter 3.2 cm, having 220 turns per cm. At its centre, a 130 turn closely packed coil of diameter 2.1 cm is placed such that the coil is coaxial with the long solenoid. The current in the solenoid is reduced to zero at a steady rate in 25 ms. What is the magnitude of emf induced in the coil while the current in the solenoid is changing?
View SolutionA small coil of N turns has its plane perpendicular to a uniform magnetic field as shown in Fig. 30-5. The coil is connected to a Ballistic galvanometer, a device designed to measure the total charge passing through it. Find the charge passing through the coil if the coil is rotated through 180° about its diameter.
View SolutionInduced emf and current due to a changing uniform B field
Figure 30-8 shows a conducting loop consisting of a half-circle of radius r = 0.20 m and three straight sections. The halfcircle lies in a uniform magnetic field `vecB` that is directed out of the page, the field magnitude is given by `B = 4.0t^(2) + 2.0t + 3.0`, with B in teslas and tin seconds. An ideal battery with emf `E_("bat")` = 2.0 V is connected to the loop. The resistance of the loop is 2.0 `Omega`.
(a) What are the magnitude and direction of the emf `E_("ind")` induced around the loop by field `vecB` at t = 10 s?
(b) What is the current in the loop at t = 10 s?
View SolutionInduced emf due to a changing nonuniform B field
Figure 30-9 shows a rectangular loop of wire immersed in a nonuniform and varying magnetic field `vecB` that is perpendicular to and directed into the page. The field's magnitude is given by `B = 4t^(2)x^(2)`, with B in teslas, tin seconds, and x in meters. (Note that the function depends on both time and position.) The loop has width W = 3.0 m and height H = 2.0 m. What are the magnitude and direction of the induced emf E around the loop at t = 0.10 s?
View SolutionWhen a rod of length l is rotated with angular velocity of `omega` in a perpendicular field of induction B , about one end , the emf across its ends is
View SolutionA coil of cross-sectional area A having n turns is placed in uniform magnetic field B. When it is rotated with an angular velocity `omega`, the maximum e.m.f. induced in the coil will be :
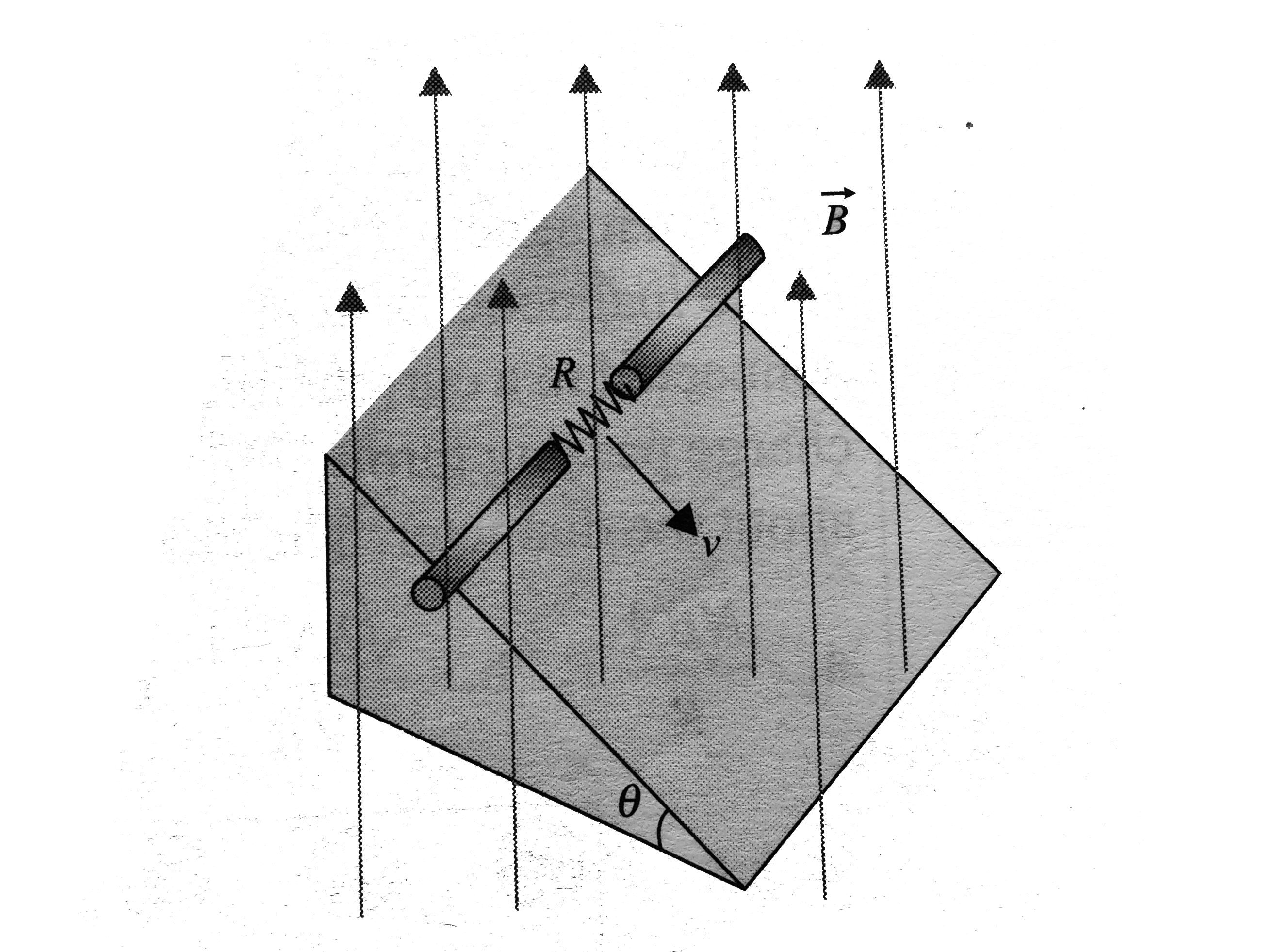
View SolutionA wire of length `l`, mass `m` and resistance `R` slides without any friction down the parallel conducting rails of negligible resistance . The rails are connected to each other at the bottom by a resistanceless rail parallel to the wire so that the wire and the rails form a closed rectangualr conducting loop. The plane of the rails makes an angle `theta` with the horizontal and a uniform vertical magnetic field of the inducetion `B` exists throughout the rregion. Find the steady state velocity of the wire.
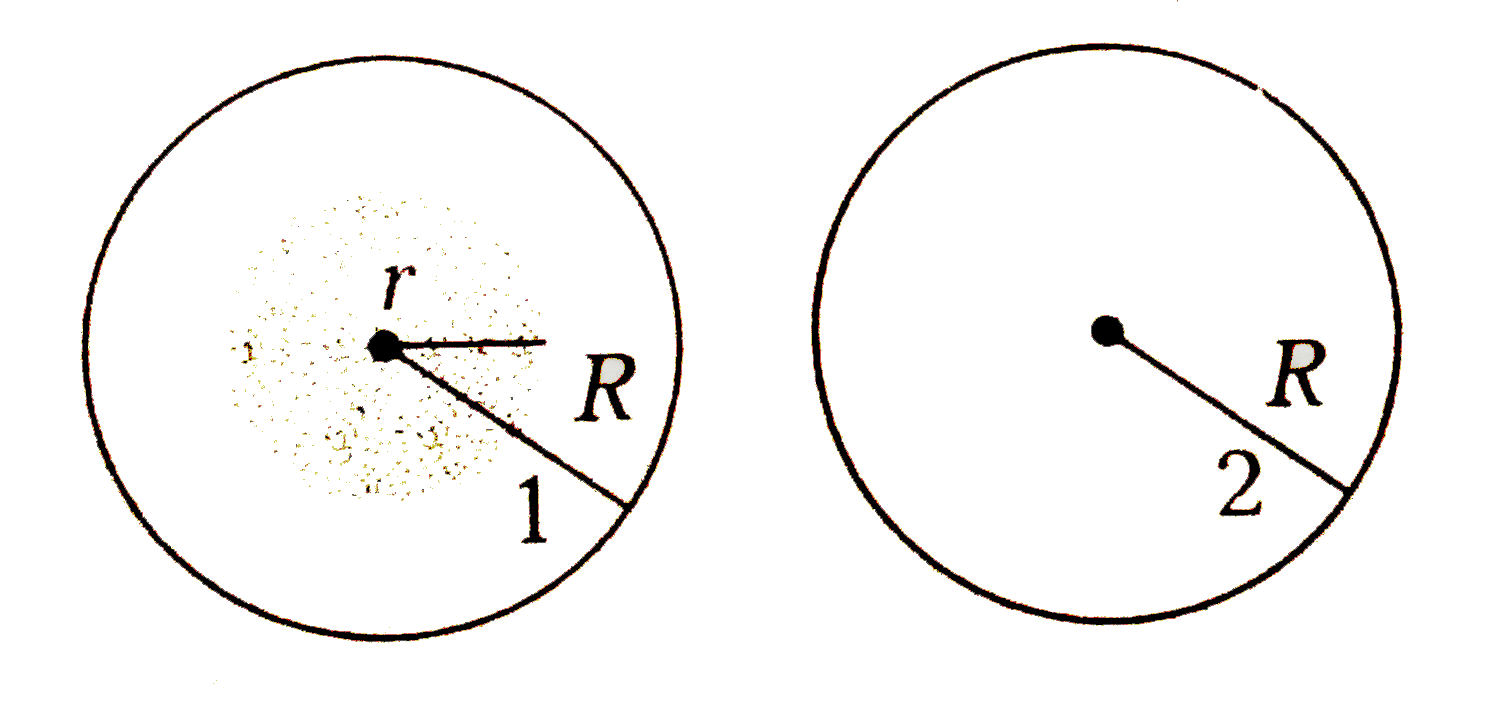
View SolutionA uniform magnetic field is restricted within a region of radius r. The magnetic field changes with time at a rate `(dB)/(dt)`. Loop 1 of radius R `gt` r encloses the region r and loop 2 of radius R is outside the region of magnetic field as shown in figure. Then, the emf generated is
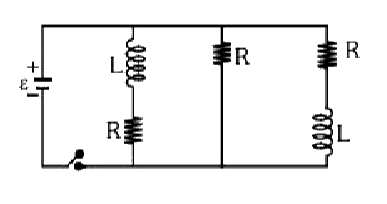
View SolutionA circuit that contains three identical resistors with resistance `R = 9.0 Omega` each, two identical inductors with inductance L = 2.0 mH each, and an ideal battery with emf `epsilon = 18 V` . The current 'i' through the battery just after the switch closed
View SolutionRL circuit, current during the transition
A solenoid has an inductance of 53 mH and a resistance of 0.37 `Omega` . If the solenoid is connected to a battery, how long will the current take to reach half its final equilibrium value? (This is a real solenoid because we are considering its small, but nonzero, internal resistance.)
View SolutionEnergy stored in a magnetic field
A coil has an inductance of 53 mH and a resistance of 0.35 `Omega`.
(a) If a 12 V emf is applied across the coil, how much energy is stored in the magnetic field after the current has built up to its equilibrium value?
(b) After how many time constants will half this equilibrium energy be stored in the magnetic field?
View SolutionFinding total energy stored in a magnetic field for a length of coaxial cable from the energy density
Finding total energy stored in a magnetic field for a length of coaxial cable from the energy density
(b) What is the stored energy per unit length of the cable if a= 1.2 mm, b = 3.5 mm, and i = 2.7 A?
View SolutionTwo circular coils, one of smaller radius `r_(1)` and the other of very large radius `r_(2)` are placed co-axially with centres coinciding. Obtain the mutual inductance of the arrangement.
View SolutionIn Fig. coil `1` and coil `2` are wound on a long cylindrical insulator. The ends `A'` and `B` are joined together and current `I` is passed. Self-inductance of the two coils are `L_(1)` and `L_(2)`, and their mutual inductance is `M`.
a. Show that this combination can be replaced by a single coil of equivalent inductanCe given by
`L_(eq) = L_(1) + L_(2) + 2M`.
b. How could the coils be reconnected by yieldings an equivalent inductance of `L_(eq) = L_(1) + L_(2) - 2M`.

View Solution
SAMPLE PROBLEMS questions and complete solutions for chapter ELECTROMAGNETIC INDUCTION of RESNICK AND HALLIDAY PHYSICS (HINGLISH) of Class 12