Complete Solutions to PROBLEMS of chapter ELECTROMAGNETIC INDUCTION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTROMAGNETIC INDUCTION |
| RESNICK AND HALLIDAY | PROBLEMS |
| Number Of Questions | 67 |
| Academic Year | 2023-24 |
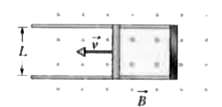
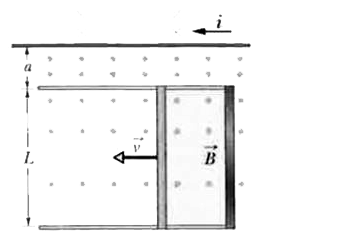
In Fig. 30-37, a metal rod is forced to move with constant velocity `vecv` along two parallel metal rails, connected with a strip of metal at one end. A magnetic field of magnitude B = 0.125 T points out of the page. ( a) If the rails are separated by L = 25.0 cm and the speed of the rod is 38.0 emfs, what emf is generated? (b) If the rod has a resistance of 18.0 `Omega` and the rails and connector have negligible resistance, what is the current in the rod? (c) At what rate is energy being transferred to thermal energy? (d) What is the magnitude of the leftward force that causes the rod to move?
View SolutionCoil 1 has `L_(1)` = 25 mH and `N_(1)` = 100 turns. Coil 2, has `L_(2)`= 40 mH and `N_(2)` = 200 turns. The coils are fixed in place, their mutual inductance M is 9.0 mH. A 6.0 mA current in coil 1 is changing at the rate of 4.0 A/s. (a) What magnetic flux `phi_(12)` 12 links coil 1, and (b) what self-induced emf appears in that coil? (c) What magnetic flux `phi_(21)` links coil 2, and (d) what mutually induced emf appears in that coil?
View SolutionThe conducting rod shown in Fig. 30-37 has length Land is being pulled along horizontal, frictionless conducting rails at a constant velocity `vecv`. The rails are connected at one end with a metal strip. A uniform magnetic field `vecB`, directed out of the page, fills the region in which the rod moves. Assume that L = 10 cm, v = 5.0 m/s, and B = 1.2 T. What are the (a) magnitude and (b) direction (up or down the page) of the emf induced in the rod? What are the (c) size and (d) direction of the current in the conducting loop? Assume that the resistance of the rod is 0.40 `Omega` and that the resistance of the rails and metal strip is negligibly small. (e) At what rate is thermal energy being generated in the rod? (f) What external force on the rod is needed to maintain `vecv`? (g) At what rate does this force do work on the rod?
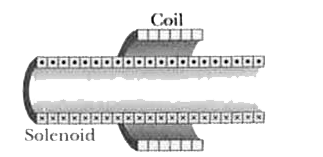
View SolutionA coil C of N turns is placed around a long solenoid S of radius R and n turns per unit length, as in Fig. 30-38.
(a) Show that the mutual inductance for the coil-solenoid combination is given by `M = μ_(0)piR^(2)nN`.
(b) Explain why M does not depend on the shape, size, or possible lack of close packing of the coil.

View SolutionIf 50.0 cm of copper wire (diameter= 3.00 mm) is formed into a circular loop and placed perpendicular to a uniform magnetic field that is increasing at the constant rate of 30.0 mT/s, at what rate is thermal energy generated in the loop?
View SolutionFigure 3.188 shows two parallel and coaxial loops. The smaller loop (radius r) is above the larger loop (radius R), by distance `x gtgt R`. The magnetic field due to current `i` in the larger loop is nearly constant throughout the smaller loop. Suppose that `x` is increasing at a constant rate of `dx//dt = v`.

The induced emf in the smaller loop is
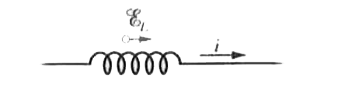
View SolutionSuppose the emf of the battery, the circuit shown varies with time `t` so the current is given by `i(t)=3+5t`, where `i` is in amperes & `t` is in seconds. Take `R=4Omega, L=6H` & find an expression for the battery emf as function of time.

View SolutionThe magnetic field of a cylindrical magnet that has a poleface diameter of 3.3 cm can be varied sinusoidally between 29.6 T and 31.2 T at a frequency of 15 Hz. (The current in a wire wrapped around a permanent magnet is varied to give this variation in the net field.) At a radial distance of 1.6 cm, what is the amplitude of the electric field induced by the variation?
View SolutionAt t = 0, a battery is connected to a series arrangement of a resistor and an inductor. At what multiple of the inductive time constant will the energy stored in the inductor's magnetic field be 0.500 of its steady-state value?
View SolutionA 12 H inductor carries a current of 2.0 A. At what rate must the current be changed to produce a 60 V emf in the inductor?
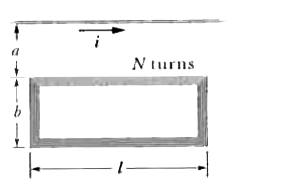
View SolutionA rectangular loop of N closely packed turns is positioned near a long straight wire as shown in Fig. 30-40. What is the mutual inductance M for the loop-wire combination if N = 150, a = 1.0 cm, b = 9.5 cm, and l = 30 cm?
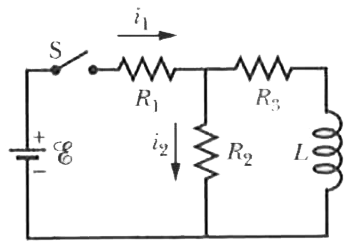
View SolutionIn Fig. 30-41, E = 100 V, `R_(1) = 10.0 Omega, R_(2) = 20.0 Omega , R_(3) = 31.0 Omega` , and L = 2.00 H. Immediately after switch S is closed, what are (a) `i_(1)` and (b) `i_(2)`? (Let currents in the indicated directions have positive values and currents in the opposite directions have negative values.) A long time later, what are (c) `i_(1)` and (d) `i_(2)`? The switch is then reopened. Just then, what are (e) `i_(1)` and (f) `i_(2)`? A long time later, what are (g) `i_(1)` and (h) `i_(2)`?
View SolutionA coil is connected in series with a 10.0 `kOmega` resistor. An ideal 50.0 V battery is applied across the two devices and the current reaches a value of 2.00 mA after 5.00 ms. (a) Find the inductance of the coil. (b) How much energy is stored in the coil at this same moment?
View SolutionTwo coils are at fixed locations. When coil 1 has no current and the current in coil 2 increases at the rate 21.0 A/s, the emf in coil 1 is 25.0 mV. (a) What is their mutual inductance? (b) When coil 2 has no current and coil 1 has a current of 1.35 A, what is the flux linkage in coil 2?
View SolutionThe switch in Fig. 30-28 is closed on a at time t = 0. What is the ratio `E_(L)//E` of the inductor's self-induced emf to the battery's emf (a) just after t = 0 and (b) at t = 2.00 `tau_(L)`? (b) At what multiple of `tau_(L)`, will `E_(L)//E = 0.500`?
View SolutionTwo identical long wires of radius a = 0.530 mm are parallel and carry identical currents in opposite directions. Their center-to-center separation is d = 20.0 cm. Neglect the flux within the wires but consider the flux in the region between the wires. What is the inductance per unit length of the wires?
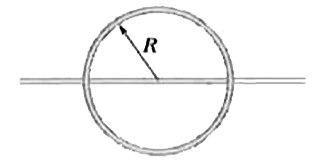
View SolutionIn Fig. 30-42, a wire forms a closed circular loop, of radius R = 0.32 m and resistance 0.056 `Omega`. The circle is centered on a long straight wire, at time t = 0, the current in the long straight wire is 5.0 A rightward. Thereafter, the current changes according to i = `5.0 A - (2.0 A//s^(2))t^(2)`. (The straight wire is insulated, so there is no electrical contact between it and the wire of the loop.) What is the magnitude of the current induced in the loop at times `t gt 0`?
View SolutionThe current in an RL circuit drops from 2.30 A to 3.40 mA in 0.025 s following removal of the battery from the circuit. If L is 10 H, find the resistance R in the circuit.
View SolutionA coil with an inductance of 2.0 Hand a resistance of 10 `Omega` is suddenly connected to an ideal battery with E = 100 V. At 0.10 s after the connection is made, what is the rate at which (a) energy is being stored in the magnetic field, (b) thermal energy is appearing in the resistance, and ( c) energy is being delivered by the battery?
View SolutionA length of copper wire carries a current of 3.5 A uniformly distributed through its cross section. Calculate the energy density of (a) the magnetic field and (b) the electric field at the surface of the wire. The wire diameter is 2.5 mm, and its resistance per unit length is 3.3 `Omega`/km.
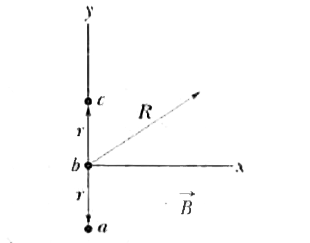
View SolutionTwo straight conducting rails form a right angle where their ends are joined. A conducting bar in contact with the rails starts at the vertex at time t = 0 and moves with constant velocity v along them as shown in Fig. A magnetic field `vec(B)` is directed into the page. the induced emf in the circuit at any time t is proportional to

View SolutionA solenoid having an inductance of 9.70 μH is connected in series with a 1.20 `kOmega` resistor. (a) If a 14.0 V battery is connected across the pair, how long will it take for the current through the resistor to reach 40.0% of its final value? (b) What is the current through the resistor at time `t = 0.50tau_(L)`?
View SolutionA solenoid that is 85.0 cm long has a cross-sectional area of 17.0 `cm^(2).` There are 1210 turns of wire carrying a current of 6.60 A. (a) Calculate the energy density of the magnetic field inside the solenoid. (b) Find the total energy stored in the magnetic field there (neglect end effects).
View SolutionA rectangular loop (area = 0.15 `m^(2)`) turns in a uniform magnetic field, B = 0.20 T. When the angle between the field and the normal to the plane of the loop is `pi//2` rad and increasing at 0.60 rad/s, what emf is induced in the loop?
View SolutionFor the circuit of Fig. 30-29, assume that ~ = 10.0 V, R = `112 Omega`, and L = 5.50 H. The ideal battery is connected at time t = 0. (a) How much energy is delivered by the battery during the first 2.00 s? (b) How much of this energy is stored in the magnetic field of the inductor? (c) How much of this energy is dissipated in the resistor?
View SolutionIn Fig. 30-44, after switch S is closed at time t = 0, the emf of the source is automatically adjusted to maintain a constant current i through S. (a) Find the current through the inductor as a function of time. (b) At what time is the current through the resistor equal to the current through the inductor?

View SolutionA toroidal inductor with an inductance of 90 mH encloses a volume of 0.0200 `m^(3)`. If the average energy density in the toroid is 70.0 J/`m^(3)`, what is the current through the inductor?
View SolutionTwo solenoids are part of the spark coil of an automobile. When the current in one solenoid fails from 6.0 A to zero in 2.5 ms, an emf of 31 kV is induced in the other solenoid. What is the mutual inductance M of the solenoids?
View SolutionA small circular loop of area 2.00 c`m^(2)` is placed in the plane of, and concentric with, a large circular loop of radius 1.00 m. The current in the large loop is changed at a constant rate from 50.0 A to -50.0 A (a change in direction) in a time of 1.00 s, starting at t= 0. What is the magnitude of the magnetic field B at the center of the small loop due to the current in the large loop at (a) t = 0, (b) t = 0.500 s, and ( c) t = 1.00 s? ( d) From t= 0 to t= 1.00 s, is `vecB` reversed? Because the inner loop is small, assume `vecB` is uniform over its area. (e) What emf is induced in the small loop at t = 0.500 s?
View SolutionIn Fig. 30-45 , a rectangular loop of wire with length a= 2.2 cm, width b = 0.80 cm, and resistance R = 0.40 mn is placed near an infinitely long wire carrying current i = 4.7 A. The loop is then moved away from the wire at constant speed v = 3.2 mm/s. When the center of the loop is at distance r = 1.5b, what are (a) the magnitude of the magnetic flux through the loop and (b) the current induced in the loop?
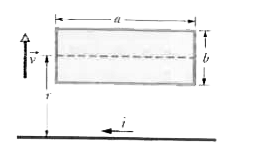
View SolutionIn Fig. 30-46, a stiff wire bent into a semicircle of radius a = 1.4 cm is rotated at constant angular speed 30 rev/s in a uniform 20 mT magnetic field. What are the (a) frequency and (b) amplitude of the emf induced in the loop?
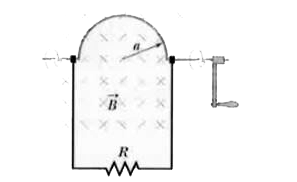
View SolutionThe current in an RL circuit builds up to one-third of its steady-state value in 5.00 s. Find the inductive time constant.
View SolutionAs seen in Fig. 30-47, a square loop of wire has sides of length 3.0 cm. A magnetic field is directed out of the page, its magnitude is given by `B = 5.0t^(2)y` , where B is in teslas, t is in seconds, and y is in meters. At t = 2.5 s, what are the (a) magnitude and (b) direction of the emf induced in the loop?

View SolutionWhat must be the magnitude of a uniform electric field if it is to have the same energy density as that possessed by a 20 mT magnetic field?
View SolutionA long solenoid has a diameter of 12.0 cm. When a current i exists in its windings, a uniform magnetic field of magnitude B = 30.0 mT is produced in its interior. By decreasing i, the field is caused to decrease at the rate of 6.50 mT/s. Calculate the magnitude of the induced electric field (a) 4.20 cm and (b) 10.3 cm from the axis of the solenoid.
View SolutionTwo inductances `L_(1)` & `L_(2)` are connected in series & are seperated by a large distance.
(a) Show that their equivalent inductance is `L_(1)+L_(2)`.
(b) Why must their seperation be larger ?
View SolutionTwo coils connected as shown in Fig. 30-48 separately have inductances `L_(1)` and `L_(2)`. Their mutual inductance is M. (a) Show that this combination can be replaced by a single coil of equivalent inductance given by
`L_(eq)=L_(1)+L_(2)+2M`
(b) How could the coils in Fig. 30-48 be reconnected to yield an equivalent inductance of
`L_(eq)=L_(1)+L_(2)-2M`?
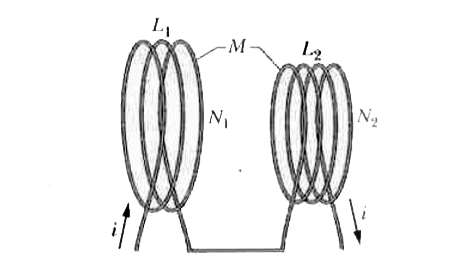
View SolutionInductors in parallel. Two inductors `L_(1)` and `L_(2)` are connected in parallel and separated by a large distance so that the magnetic field of one cannot affect the other. (a) Show that the equivalent inductance is given by
`1/(L_(eq))=1/(L_(1))=1/(L_(2))`
(Hint: Review the derivations for resistors in parallel and capacitors in parallel. Which is similar here?) (b) What is the generalization of (a) for N inductors in parallel?
View SolutionA small loop of area 3.1 m`m^(2)` is placed inside a long solenoid that has 672 turns/cm and carries a sinusoidally varying current i of amplitude 1.28 A and angular frequency 212 rad/s. The central axes of the loop and solenoid coincide. What is the amplitude of the emf induced in the loop?
View SolutionAt a certain place, Earth's magnetic field has magnitude B = 0.590 gauss and is inclined downward at an angle of 70.0° to the horizontal. A flat horizontal circular coil of wire with a radius of 10.0 cm has 1000 turns and a total resistance of 85.0 `Omega`. It is connected in series to a meter with 140 `Omega` resistance. The coil is flipped through a half revolution about a diameter, so that it is again horizontal. How much chHrge flows through the meter during the flip?
View SolutionA square wire loop with 2.00 m sides is perpendicular to a uniform magnetic field, with half the area of the loop in the field as shown in Fig. 30-49. The loop contains an ideal battery with emf E = 12.0 V. If the magnitude of the field varies with time according to B = 0.603 - 1.25t, with B in teslas and I in seconds, what are (a) the net emf in the circuit and (b) the direction of the (net) current around the loop?
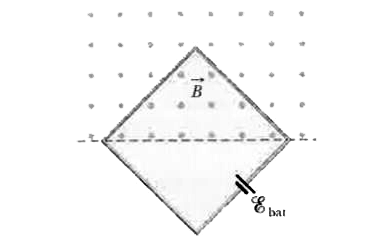
View SolutionFigure 30-50 shows a rod of length L = 12.0 cm that is forced to move at constant speed v = 5.00 m/s along horizontal rails. The rod, rails, and connecting strip at the right form a conducting loop. The rod has resistance 0.400 `Omega` the rest of the loop has negligible resistance. A current i = 100 A through the long straight wire at distance a= 5.00 mm from the loop sets up a (nonuniform) magnetic field through the loop. Find the (a) emf and (b) current induced in the loop. (c) At what rate is thermal energy generated in the rod? (d) What is the magnitude of the force that must be applied to the rod to make it move at constant speed? (e) At what rate does this force do work on the rod?
View SolutionA wooden toroidal core with a square cross section has an inner radius of 10 cm and an outer radius of 12 cm. It is wound with one layer of wire (of diameter 1.0 mm and resistance per meter 0.020 `Omega` /m). What are (a) the inductance and (b) the inductive time constant of the resulting toroid? Ignore the thickness of the insulation on the wire.
View SolutionAt a given instant the current and self-induced emf in an inductor are directed as indicated in Fig. 30-51. (a) ls the current increasing or decreasing? (b) The induced emf is 23 V, and the rate of change of the current is 18 kA/s, find the inductance.
View SolutionA battery is connected to a series RL circuit at time t = 0. At what multiple of `tau_(L)` will the current be 1.00% less than its equilibrium value?
View SolutionA circular region in an xy plane is penetrated by a uniform magnetic field in the positive direction of the z axis. The field's magnitude B (in teslas) increases with time t (in seconds) according to B = at, where a is a constant. The magnitude E of the electric field set up by that increase in the magnetic field is given by Fig. 30-52 versus radial distance r, the vertical axis scale is set by `E_(s) = 310 μN//C`, and the horizontal axis scale is set by `r_(s)` = 4.00 cm. Find a.

View SolutionA circular coil has a 15.0 cm radius and consists of 30.0 closely wound turns of wire. An externally produced magnetic field of magnitude 2.60 mT is perpendicular to the coil. (a) If no current is in the coil, what magnetic flux links its turns? (b)When the current in the coil is 2.80 A in a certain direction, the net flux through the coil is found to vanish. What is the inductance of the coil?
View SolutionA certain elastic conducting material is stretched into a circular loop of 12.0 cm radius. It is placed with its plane perpendicular to a uniform 0.800 T magnetic field. When released, the radius of the loop starts to shrink at an instantaneous rate of 75.0 emfs. What emf is induced in the loop at that instant?
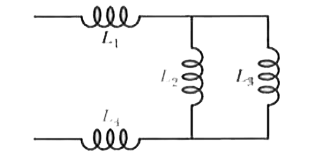
View SolutionThe inductor arrangement of Fig. 30-53, with `L_(1)` = 50.0 mH, `L_(2)` = 80.0 mH, `L_(3)` = 20.0 mH, and `L_(4)` = 15.0 mH, is to be connected to a varying current source. What is the equivalent inductance of the arrangement?
View SolutionTwo long, parallel copper wires of diameter 4.0 mm carry currents of 7.0 A in opposite directions. (a) Assuming that their central axes are 20 mm apart, calculate the magnetic flux per meter of wire that exists in the space between those axes. (b) What percentage of this flux lies inside the wires? (c) Repeat part (a) for parallel currents.
View SolutionIn Fig. 30-54, a 120-turn coil of radius 1.8 cm and resistance 5.3 `Omega` is coaxial with a solenoid of 220 turns/cm and diameter 3.2 cm. The solenoid current drops from 0.42 A to zero in time interval `Deltat = 0.67` s. What current is induced in the coil during `Deltat`?
View SolutionA loop antenna of area 2.00 `cm^(2)` and resistance 5.21 `μOmega`. is perpendicular to a uniform magnetic field of magnitude 17.0 μT. The field magnitude drops to zero in 2.96 ms. How much thermal energy is produced in the loop by the change in field?
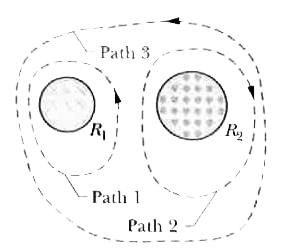
View SolutionFigure 30-55 shows two circular regions `R_(1)` and `R_(2)` with radii `r_(1)` = 20.0 cm and `r_(2)` = 31.0 cm. In `R_(1)` there is a uniform magnetic field of magnitude `B_(1)`= 50.0 mT directed into the page, and in `R_(2)` there is a uniform magnetic field of magnitude `B_(2)` = 75.0 mT directed out of the page (ignore fringing) . Both fields are decreasing at the rate of 8.50 mT/s. Calculate `intovecE.dvecs` for (a) path 1, (b) path 2, and (c) path 3.
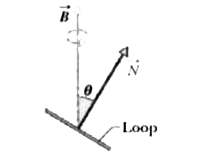
View SolutionIn Fig. 30-56, a circular loop of wire 10 cm in diameter (seen edge-on) is placed with its normal `vecN` at an angle `theta` = 20° with the direction of a uniform magnetic field `vecB` of magnitude 1.5 T. The loop is then rotated such that `vecN` rotates in a cone about the field direction at the rate 100 rev/min, angle `theta` remains unchanged during the process. What is the emf induced in the loop?
View SolutionThe inductance of a closely packed coil of 400 turns is 8.0 mH. Calculate the magnetic flux through the coil when the current is 5.0 mA.
View SolutionOne hundred turns of (insulated) copper wire are wrapped around a wooden cylindrical core of cross-sectional area `1.90 xx 10^(-3) m^(2)`. The two ends of the wire are connected to a resistor. The total resistance in the circuit is 9.50 `Omega`. If an externally applied uniform longitudinal magnetic field in the core changes from 1.60 T in one direction to 1.60 T in the opposite direction, how much charge flows through a point in the circuit during the change?
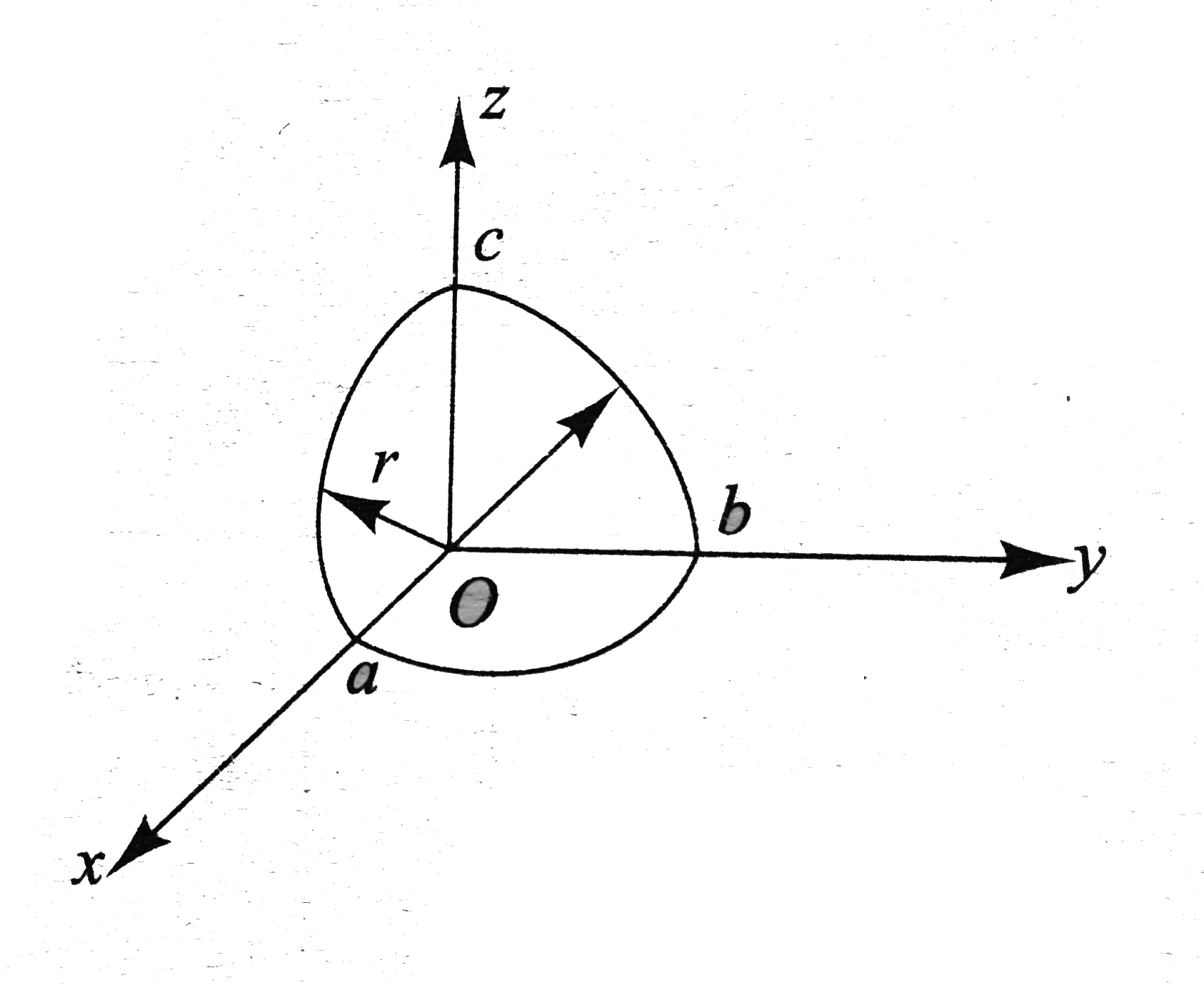
View SolutionA wire is bent into three circular segment of radius `r = 10 cm` as shown in. Each segment is a quadrant of a circle `ab` lying in the `x-y` plane, `bc` lying in the `y-z` plane and `ca` lying in the `z-x` plane.
(a) if a magnetic field `B` points in the positive `x` direction, what is the magnitude of the emf developed in the wire when `B` increases at the rate of `3 mTs^(-1)`?
(b) What is the direction of the current in the segment `bc`.
View SolutionIn Fig. 30-58, R = 15 `Omega`, L = 15 H , the ideal ba ttery has E = 10 V, and the fuse in the upper branch is an ideal 3.0 A fuse. It has zero resistance as long as the current through it remains less than 3.0 A. lf the current reaches 3.0 A, the fuse "blows" and thereafter has infinite resistance. Switch S is closed at time t = 0. (a) When does the fuse blow? (b) Sketch a graph of the current i through the inductor as a function of time. Mark the time at which the fuse blows.

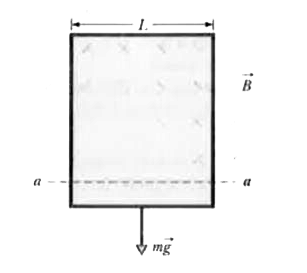
View SolutionIn Fig. 30-59, a long rectangular conducting loop, of width L , resistance R, and mass m, is hung in a horizontal, uniform magnetic field `vecB` that is directed into the page and that exists only above line aa. The loop is then dropped, during its fall , it accelerates until it reaches a certain terminal speed `v_(t)`. Ignoring air drag, find an expression for `v_(t)`.
View SolutionIn Fig. 30-60, the magnetic flux through the loop increases according to the relation `phi_(B) = 3.0t^(2) = 7.0t`, where `phi_(B)` is in milliwebers and tis in seconds. (a) What is the magnitude of the emf induced in the loop when t = 1.5 s? (b) Is the direction of the current through R to the right or left?

View SolutionFigure 30-61 shows a uniform magnetic field `vecB` confined to a cylindrical volume of radius R. The magnitude of `vecB` is decreasing at a constant rate of 10 mT/s. In unit-vector notation, what is the initial acceleration of an electron released at (a) point a (radial distance r = 5.0 cm), (b) point b (r = 0), and (c) point c (r = 5.0 cm)?
View SolutionA square loop 10 cm to a side is placed on a wooden table in a uniform magnetic field of magnitude 0.25 T. It is found that the biggest magnetic flux through the loop is measured when the loop is flat on the table. What is the flux through the loop when it is tilted such that the plane of the loop makes a 60° angle with the table?
View SolutionThe magnetic flux through each of give faces of a neutral playing dice is given `phi_(B)=+-NWb, where N(=1 t o 5)` is the number of spots on the face. The flux is positive (out -ward) for `N` even and negative (inward) for `N` odd What is the flux through sixth face of the die ?
View SolutionInitially there is no magnetic flux through a certain conducting loop. A magnetic field near the loop is then suddenly turned on, and 5 s later, the magnetic flux through the loop is 1.0 `Tm^(2)`. What is the average magnitude of the induced emf in the loop during those 5 s?
View SolutionAt the Earth's equator, B is horizontal and to the north, with a magnitude of approximately `7 xx 10^(-5) T`. (a) What is the magnetic flux through a loop of radius 0.1 m, lying flat on the ground? (b) If the same loop is balanced on its edge such that its axis points northwest, what is the magnetic flux through the loop? (c) If the loop is now rotated such that its axis points north, what is the magnetic flux through the loop? (d) If the loop is now rotated such that its axis points west, what is the magnetic flux through the loop?
View SolutionAn airliner with a wingspan of 33.5 m travels toward the east at a speed of 280 m/s in a region where the Earth's magnetic field is `4.2 xx 10^(-5)` T directed toward the north and 53° below horizontal. (a) What is the induced emf between the plane's wingtips? (b) Will a bulb glow if we connect the tip of wings by a conducting wire with a bulb in between?
View SolutionA cubical region of space with side lengths 0.05 m contains a uniform magnetic field. If the total magnetic energy stored in this region is `pi` J, what is the magnitude of the magnetic field?
View Solution
PROBLEMS questions and complete solutions for chapter ELECTROMAGNETIC INDUCTION of RESNICK AND HALLIDAY PHYSICS (HINGLISH) of Class 12