Complete Solutions to PRACTICE QUESTIONS (Link Comprehension) of chapter PHOTONS AND MATTER WAVES of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | PHOTONS AND MATTER WAVES |
| RESNICK AND HALLIDAY | PRACTICE QUESTIONS (Link Comprehension) |
| Number Of Questions | 17 |
| Academic Year | 2023-24 |
which of the following are not dependent on the intensity of the incident radiation in a photoelectric experiment?
View SolutionIt is desired to obtain a diffraction pattern for electrons using a diffraction grating with lines separated by 10 nm. The mass of an electron is `9.11 xx 10^(-31)kg.`
What is the approximate kinetic energy of electrons that would be diffracted by such a grating?
View SolutionIt is desired to obtain a diffraction pattern for electrons using a diffraction grating with lines separated by 10 nm. The mass of an electron is `9.11 xx 10^(-31)kg.`
Suppose it is desired to observe diffraction effects for a beam of electromagnetic radiation using the same grating. Roughly, what is the required energy of the individual photons in the beam?
View SolutionA physicist wishes to eject electrons by shining light on a metal surface. The light source emits light of wavelength of 450 nm. The table lists the only available metals and their work functions.
`{:("Metal",W_(0)(eV)),("Barium",2.5),("Lithium",2.3),("Tantalum",4.2),("Tungsten",4.5):}`
Which metal(s) can be used to produce electrons by the photoelectric effect from given source of light?
View SolutionA physicist wishes to eject electrons by shining light on a metal surfac. The light source emits light of wavelenght of 450 nm. The table lists the only available metals and their work functions.
`{:("Metal",W_(0)(eV)),("Barium",2.5),("Lithium",2.3),("Tantalum",4.2),("Tungsten",4.5):}`
Which option correctly identifies the metal that will produce the most energetic electrons and their energies?
View SolutionWhen a particle is restricted to move aong `x`axis between `x =0` and `x = a`, where a is of nanometer dimension. Its energy can take only certain specific values. The allowed energies of the particle moving in such a restricted region, correspond to the formation of standing waves with nodes at its ends `x = 0` and `x = a`. The wavelength of this standing wave is realated to the linear momentum `p` of the particle according to the de Breogile relation. The energy of the particl e of mass m is reelated to its linear momentum as `E = (p^(2))/(2m)`. Thus, the energy of the particle can be denoted by a quantum number `'n'` taking values `1,2,3,"......."`(`n=1`, called the ground state) corresponding to the number of loop in the standing wave.
Use the model decribed above to answer the following three questions for a particle moving in the line `x = 0` to `x =a`. Take `h = 6.6 xx 10^(-34) J s` and `e = 1.6 xx 10^(-19) C`.
The allowed energy for the particle for a particular value of n is proportional to
View SolutionWhen a particle is restricted to move aong `x`axis between `x =0` and `x = a`, where a is of nanometer dimension. Its energy can take only certain specific values. The allowed energies of the particle moving in such a restricted region, correspond to the formation of standing waves with nodes at its ends `x = 0` and `x = a`. The wavelength of this standing wave is realated to the linear momentum `p` of the particle according to the de Breogile relation. The energy of the particl e of mass m is reelated to its linear momentum as `E = (p^(2))/(2m)`. Thus, the energy of the particle can be denoted by a quantum number `'n'` taking values `1,2,3,"......."`(`n=1`, called the ground state) corresponding to the number of loop in the standing wave.
Use the model decribed above to answer the following three questions for a particle moving in the line `x = 0` to `x =a`. Take `h = 6.6 xx 10^(-34) J s` and `e = 1.6 xx 10^(-19) C`.
The speed of the particle, that can take disrete values, is proportional to
View SolutionWave property of electron implies that they will show diffraction effected . Davisson and Germer demonstrated this by diffracting electron from crystals . The law governing the diffraction from a crystals is obtained by requiring that electron waves reflected from the planes of atoms in a crystal interfere constructiely
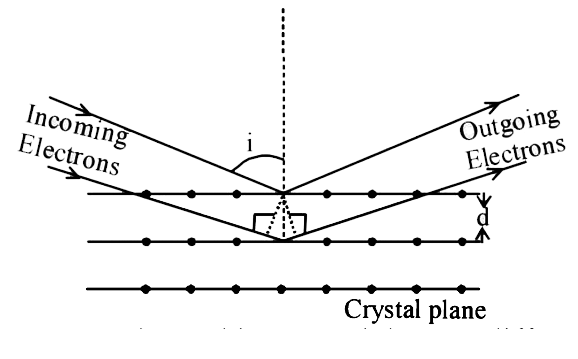
Electron accelerated by potential `V` are diffracted from a crystal if `d = 1 Å and i = 30^(@), V` should be about `(h = 6.6 xx 10^(-34) Js, m_(e) = 9.1 xx 10^(-31) kg , e = 1.6 xx 10^(-19)C)`
View SolutionWave property of electron implies that they will show diffraction effected . Davisson and Germer demonstrated this by diffracting electron from crystals . The law governing the diffraction from a crystals is obtained by requiring that electron waves reflected from the planes of atoms in a crystal inter fere constructiely
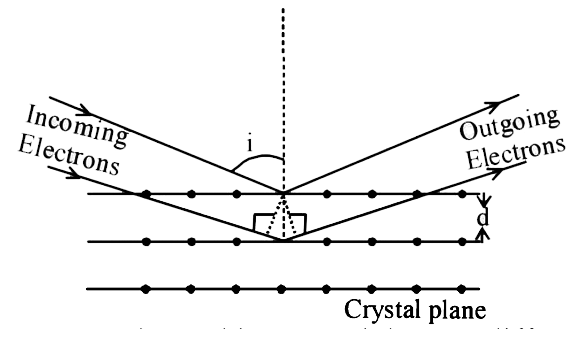
If a strong diffraction peak is observed when electrons are incident at an angle `i` from the normal to the crystal planes with distance `d` between them (see fig) de Brogle wavelength `lambda_(dB)` of electrons can be calculated by the relationship (n is an intenger)
View SolutionPhotoelectrons ar ejected from a surface when light of wavelenght `lamda_1=550 nm` is incident on it. The stopping potential for such electrons is `lamda_(S1)=0.19V`. Suppose that radiation of wavelength `lamda_2=190nm` is incident of the surface.
Q. Calculate the stopping potential `V_(S2)`.
View SolutionPhotoelectrons ar ejected from a surface when light of wavelenght `lamda_1=550 nm` is incident on it. The stopping potential for such electrons is `lamda_(S1)=0.19V`. Suppose that radiation of wavelength `lamda_2=190nm` is incident of the surface.
Q. Calulate the work function of the surface.
View SolutionPhotoelectrons ar ejected from a surface when light of wavelenght `lamda_1=550 nm` is incident on it. The stopping potential for such electrons is `lamda_(S1)=0.19V`. Suppose that radiation of wavelength `lamda_2=190nm` is incident of the surface. ltbRgt Q. Calculate the threshold frequency for the surface.
View SolutionWhen a surface is irradiated with light of wavelength `4950 Å`, a photocurrent appears which vanishes if a retarding potential greater than 0.6 volt is applied across the phototube. When a second source of light is used, it is found that the critical potential is changed to 1.1 volt.
The work- function of the emitting surface is i
View SolutionWhen a surface is irradiated with light of wavelength `4950 Å`, a photocurrent appears which vanishes if a retarding potential greater than 0.6 volt is applied across the phototube. When a second source of light is used, it is found that the critical potential is changed to 1.1 volt.
The wavelength of the second source is
View SolutionWhen a surface is irradiated with a light of wavelength `4950 Å`, a photocurrent appears which vanishes if a retarding potential greater that 0.6 V is applied across the phototube. When a different source of light is used, it is found that the critical retarding potential is changed to 1.1 V.
Change in two stopping potentials is
View SolutionIn Young’s double slit experiment an electron beam is used to form a fringe pattern instead of light. If speed of the electrons is increased then the fringe
View SolutionA beam of electrons with speed `v_(0)` passes through double slits and then is allowed to strike a fluorescent screen. An interference pattern is observed on the screen.
The electrons are instead replaced by protons moving with speed `v_(0)` Compared to electrons at the same speed, what happens to the spacing of the interference fringes on the screen?
View Solution
PRACTICE QUESTIONS (Link Comprehension) questions and complete solutions for chapter PHOTONS AND MATTER WAVES of RESNICK AND HALLIDAY PHYSICS (HINGLISH) of Class 12