Complete Solutions to SAMPLE PROBLEM of chapter PHOTONS AND MATTER WAVES of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | PHOTONS AND MATTER WAVES |
| RESNICK AND HALLIDAY | SAMPLE PROBLEM |
| Number Of Questions | 10 |
| Academic Year | 2023-24 |
A sodium vapour lamp is placed at the center of a large sphere that aborbs all the light reaching it. The rate at which the lamp emits energy is 100 W, assume that the emission is entirely at a wavelength of 590 nm. At what rate are photons absorbed by the sphere?
View SolutionIf the threshold wavelength for sodium is `5420 Å`, then the work function of sodium is
View SolutionA potassium foil is a distance `r=3.5m` from an isotropic light source that emits energy at the rate `P=1.5W`. The work function F of potassium is 2.2 eV. Suppose that the energy transported by the incident light were transferred to the target foil continuously and smoothly (that is, if classical physics prevailed instead of quantum physics). How long would it take for the foil to absorb enough energy to eject and electron? Assume that the foil totally absorbs all the energy reaching it can that the to - be-ejected electron collects energy from a circular patch of the foil whose radius is `5.0xx10^(-11)m`, about that of a typical atom.
View SolutionA beam of light has three wavelengths `4144 Å`, `4972 Å` and `6216 Å` with a total instensity of `3.6 xx 10^(-3) Wm^(-2)` equally distributed amongst the three wavelengths. The beam falls normally on an area `1.0 cm^2` of a clean metallic surface of work function 2.3 eV. Assume that there is no loss of light by reflection and that each energetically capable photon ejects on electron. Calculate the number of photo electrons liberated in two seconds.
View SolutionSuppose the `10^19` photons emitted per second from the 100 W lightbulb in were all focused onto a piece of black paper and absorbed. (a)Calculate the momentum of one photon and (b)estimate the force all these photons could exert on the paper.
View Solution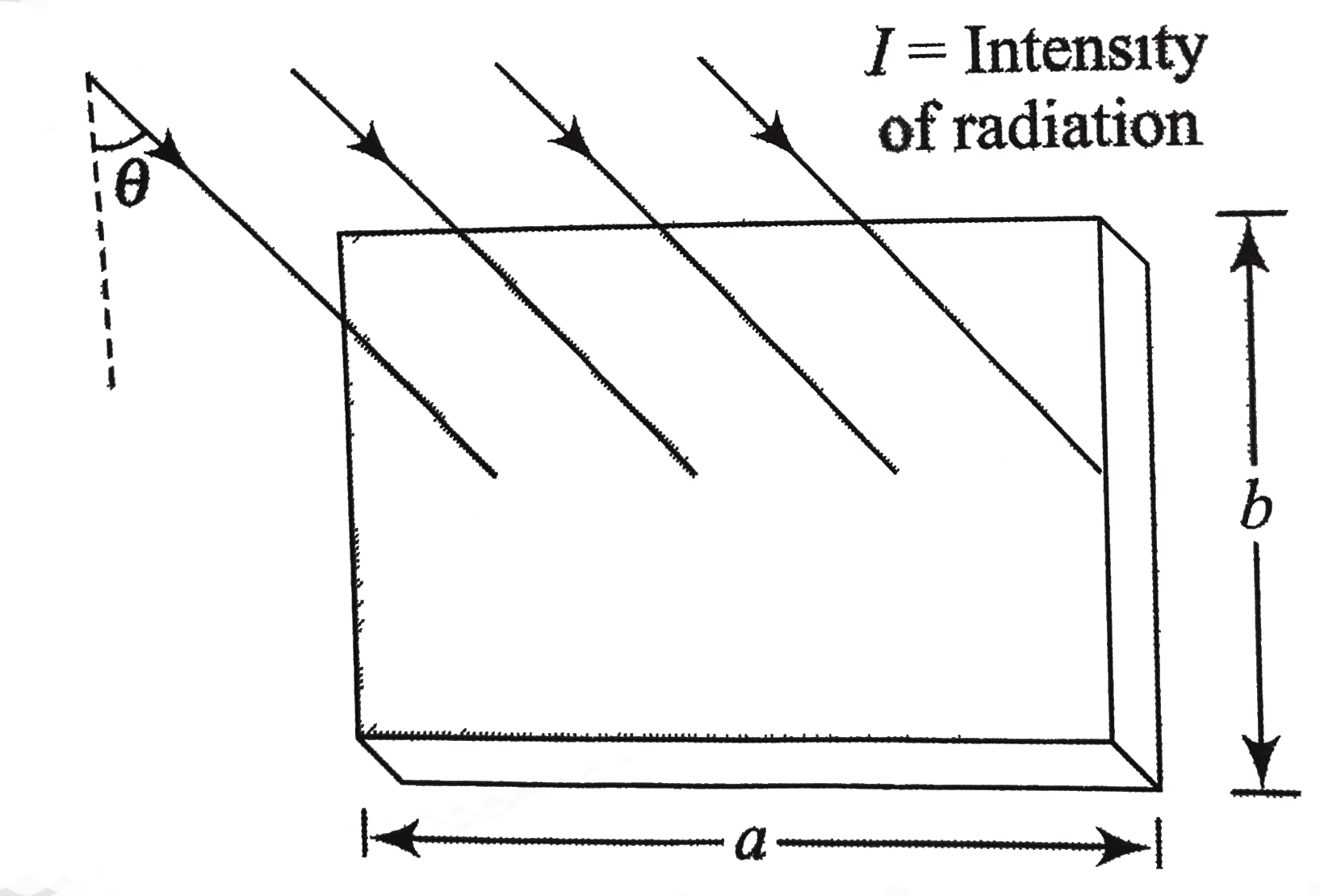
A plank of mass m is lying on a rough suface having coeffient of frinction as `mu` is situation as shown in fig Find the acceleration of the plank assuming that it slips and the surface of body exposed to radiaton is black body.
View SolutionA perfectly reflecting solid hemisphere of radius R is placed in the path of a parallel beam of light of large aperture. If the beam carrries an intensity l, find the force exerted by the beam on the hemisphere.
View SolutionFind the de-Broglie wavelength of an electron with kinetic energy of 120 eV.
View SolutionAssume that an electron is moving along an x axis and that you measure its speed to be `2.05xx10^(6)m//s`, which can be known with a precision of `0.50%`. What is the minimum uncertainty (as allowed by the uncertainty principle in quantum theory) with which you can simultaneously measure the position of the electron along the x - axis ?
Calculations : To evaluate the uncertainty `Deltap_(x)` in the momentum, we must first evaluate the momentum component `p_(x)`. Because the electron's speed `v_(x)` is much less than the speed of light c, we can evaluate `p_(x)` with the classical expression for momentum instead of using a relativistic expression. We find
`p_(x)=mv_(x)=(9.11xx10^(-31)kg)(2.05xx10^(6)m//s)`
`=1.87xx10^(-24)kg.m//s`.
The uncertainty in the speed is given as `0.50%` of the measured speed. Because `p_(x)` depends directly on speed, the uncertainty `Deltap_(x)` in the momentum must be `0.50%` of the momentum :
`Deltap_(x)=(0.0050)p_(x)`
`=(0.0050)(1.87xx10^(-24)kg.m//s)`
`=9.35xx10^(-27)kg.m//s`
Then the uncertainty principle gives us
`Deltax=(h)/(Deltap_(x))=((6.63xx10^(-34)J.s)//2pi)/(9.35xx10^(-27)kg.m//s)`
`=1.13xx10^(-18)m~~11nm`,
which is about 100 atomic diameters.
View SolutionSuppose that the electron in Fig. having a total energy E of 5.1 eV, approaches a barrier of height `U_(b)=6.8eV` and thickness L = 750 pm.
(a) What is the approximate probability that the electron will be transmitted through the barrier, to appear (and be detectable) on the other side of the barrier?
(b) What is the approximate probability that a proton with the same total energy of 5.1 eV will be transmitted through the barrier, to appear (and be detectable) on the other side of the barrier?
View Solution
SAMPLE PROBLEM questions and complete solutions for chapter PHOTONS AND MATTER WAVES of RESNICK AND HALLIDAY PHYSICS (HINGLISH) of Class 12