Complete Solutions to Problems for self practive of chapter ELECTRIC POTENTIAL AND ELECTRIC FLUX of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTRIC POTENTIAL AND ELECTRIC FLUX |
| SL ARORA | Problems for self practive |
| Number Of Questions | 61 |
| Academic Year | 2023-24 |
In a circuit, 10 C of charge is passed through a battery
. in a given time. The plates of the battery are maintained
. at a potential difference of 12 V. How much work is done
. by the battery?.
View Solution(a) Calculate the potential at a point P due to a charge of `4xx10^(-7) C` located 9 cm away.
(b) Hence obtain the work done in bringing a charge of `2xx10^(-9) C` from infinity to the point P. Does the answer depend on the path along which the charge is brought ?
View SolutionWhat must be te magnitud eof an isolated positive charge so as to produce an electric potential of `3xx10^(5)V` at a distance of 3 m from it?
View SolutionThe electric field at a point due to a point is `10NC^(-1)` and the electric potential at that point is `15JC^(-1)` Calculate the distance of the point from the charge and the magnitude of the charge.
View SolutionCharge of `12muC` is given toa hollow metallic sphere of radius 0.1 m. find the potential at (i) the surface of the sphere (ii) the centre of the sphere.
View SolutionA hollow metal sphere is charged with `0.4muC` of charge and has a radius of 0.1 find the potential (i) at the surface (ii) inside the sphere (iii) at a distance of 0.6m from the centre. The sphere is placed in air.
View SolutionCompute the electric potential at the surface of the nucleus of a silver atom. The radius of the nucleus is `3.4xx10^(-14)`m and the atomic number of silver is 47.
View SolutionEight charged drops of water, each of radius 1 m and having a charge of `10^(-10)` coulomb, combine to form a bigger drop. Determine the potential of the bigger drop.
View SolutionTwo point charges of `+10muC` and `+20muC` are placed in free space 2 cm apart. Find the electric potential at the middle point of the line joining the two charges.
View SolutionTwo point charges one of `+100 muC` and another of `-400 muC`, are kept 30 cm apart. Find the point of zero potential on the line joining the two charges.
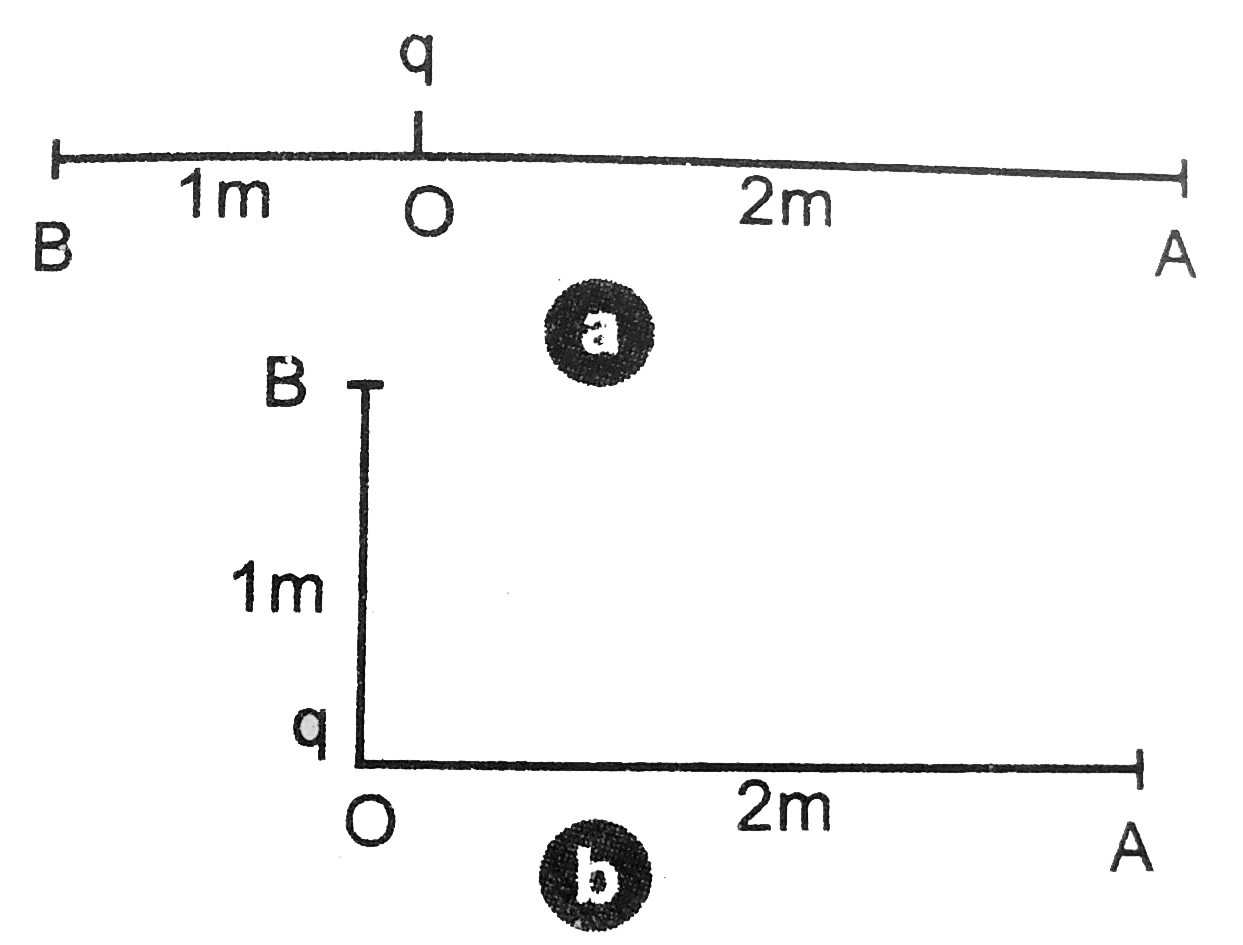
View SolutionA charge `q = + 1 muC` is held at O between two points A and B such that `AO = 2m and BO = 1m`, Fig . Calculate the value of potential differences `(V_(A) - V_(B))`. What will be the value of potential differences `(V_(A) - V_(B))` if position of B is charged as shown in Fig ?
View SolutionTwo small sphres of radius 'a' each carryig charges `+q` and `-q` and placed at points A and B, distance 'd' apart. Calculate the potential difference point A and B.
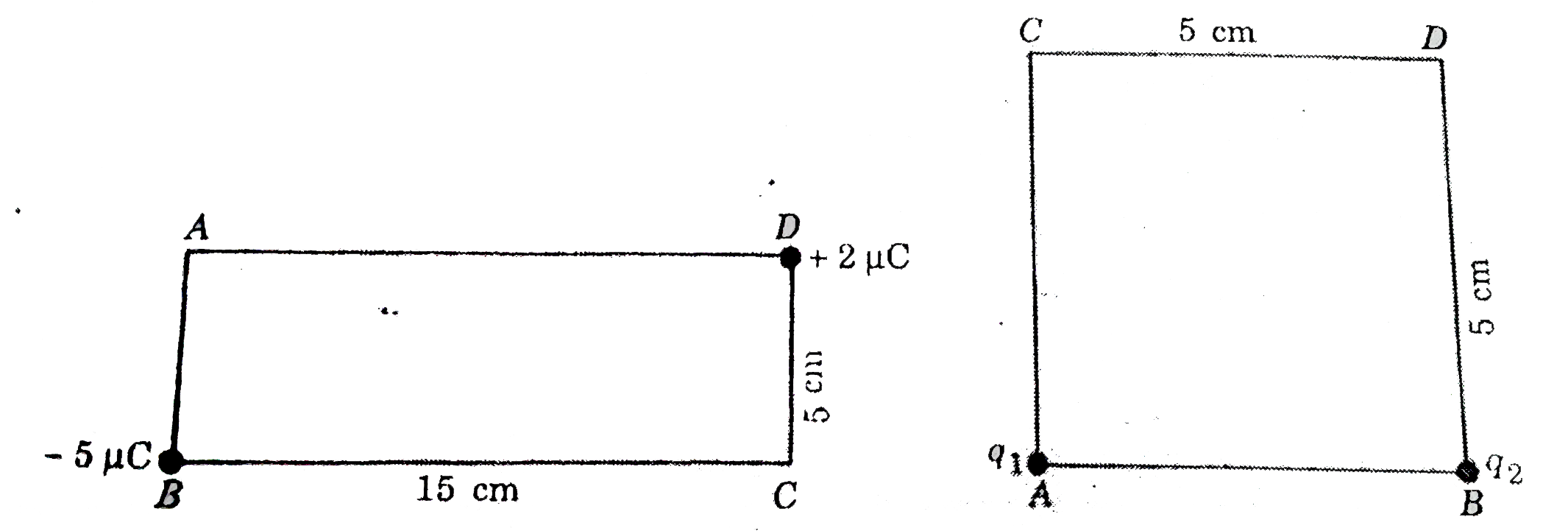
View SolutionThe sides of rectangle ABCD are 15 cm and 5 cm, as shown in figure. Point cahrges of `-5muC` and `+2muC` are placed at the vertices B and D respectively. Calculate electric potential at the vertices A and C. Also calculate the work done in carrying a charge of `3muC` from A to C.
View Solutioncharges `2.0 xx 10^(-6) C` and `1.0 xx 10^(-6) C` are placed at. corners A and B of a squae of side 5.0cm as shown in. figure .how much work will be done against. the electric field in moving a charge of `1.0 xx 10^(-6)` C from. C to D?.

View SolutionWhat is the potential at the centre of a square of each side 1.0 meter, when four charges `+1xx10^(-8)C, -2xx10^(-8) C, +3xx10^(-8)C and +2xx10^(-8)C` are placed at the four corners of the square.
View SolutionCharges of `+1.0xx10^(-11)C,-2.0xx10^(-11),+1.0xx10^(-11)C` are placed respectively at the corners B, C and D of a rectangle ABCD. Determine the potential at the corner A. given AB=4cm and BC=3cm
View SolutionABCD is a square of side `0.2m`. Charges of `2xx10^(-9) C, 4xx10^(-9) C and 8xx10^(-9) C` are placed at the corners A, B and C respectively. Calculate work required to transfer a charge of `2xx10^(-9) C` from corner D to centre of the square.
View Solutioncharges of `20nC` each are placed at the corners A and B of a square ABCD of side `sqrt(8)cm` and charges of `-10nC` at the corners C and D. find the potential at the centre of the square.
View SolutionPositive charges of 6,12 and 24 nC are placed at the thre vertices of a square. What charge must be placed at fourth vertex so that total potential at the centre of the square is zero?
View SolutionTwo equal charges, `2.0xx10^(-7) C` each, are held fixed at a separation of 20cm. A third charge of equal magnitude is placed midway between the two both the charges. How much work is done by the electric field during the process?
View SolutionThe electric potential at a point distant 0.1m from the middle of a short electric dipole on a line inclined at an angle of `60^(@)` with the dipole axis is 900V. Calculate the dipole moment.
View SolutionA uniform electric field of `20NC^(-1)` exists in the vertically downward direction. Determine the increase in the electric potential as one goes up through a height of 50 cm.
View SolutionA uniform electric field of `30NC^(-1)` exists along the X-axis calculate the potential difference `V_(B)-V_(A)` between the points A (4m,2m) and B(10m,5m).
View SolutionAn electric field `vecE = vec(i20 + vecj30 ) NC^(-1)` exists in the space. If the potential at the origin is taken to be zero find the potential at (2m, 2m).
View SolutionThe electric field in a region is given by `vecE = (A/x^3) vecI.` Write a suitable SI unit for A. Write an experssion for. the potential in the region assuming the potential at. infinity to be zero.
View SolutionCalculate the electric potential energy of an electron-proton system of an atom . The radius of the orbit of the electron is `21.16xx10^(-11)`m the charge on electron is `1.6xx10^(-19)C`.
View SolutionTwo protons in a `U^(238)` nucleus are `6.0xx10^(-15)m` apart. What is their mutual electric potential energy?
View SolutionTwo positive point charges of `12 mu C` and `8 mu C` are `10 cm` apart. The work done in bringing then `4 cm` closer is
View SolutionCharges of `+4muC,-6muC and -16muC` are placed in air at the corners of an equilateral triangle of side 10. find the potential energy of the system. `-0.72J`
View Solution
Three point charges are arranged as show in figure. What is their mutual potential energy? Take `q=1.0xx10^(-4)C and a=10cm`.
View SolutionDetermine potential energy of the charge configuration shown in figure.
View SolutionThree charges `+q, 2 q and -4q` are placed on the three vertices of an equilateral triangle of each side `0*1m`. Calculate electrostatic potential energy of the system, take `q = 10^(-7) C`
View SolutionThree charges `+q,+q and -q` are located at the corners of an equilaterial triangle of side a. Calculate potential energy of the system.
View SolutionThree particles, each having a charge of `10 muC`, are. placed at the vertices of an equilateral triabngle of side. 10 cm. Find the work done by a person in pulling them. apart to infinite separtions.
View SolutionHow much work has to be done in assembling three charged particles at the vertices of an equilateral triangle as shown in figure

View SolutionWhat is the electrostatic potential energy of the charge configuration shown in figure. Take `q_(1)=+1.0xx10^(-8)C,q_(2)=-2.0xx10^(-8)C,q_(3)=+3.0xx10^(-8)C,q_(4)=+2.0xx10^(-8)C and a=1.0`metre.
View SolutionThree charges -q, +q and -q are placed along a st. line at equal distance , say a. Calculated the potential energy of this system of charges (i) when +q charge is in the middle and (ii) when this charge is at one end.
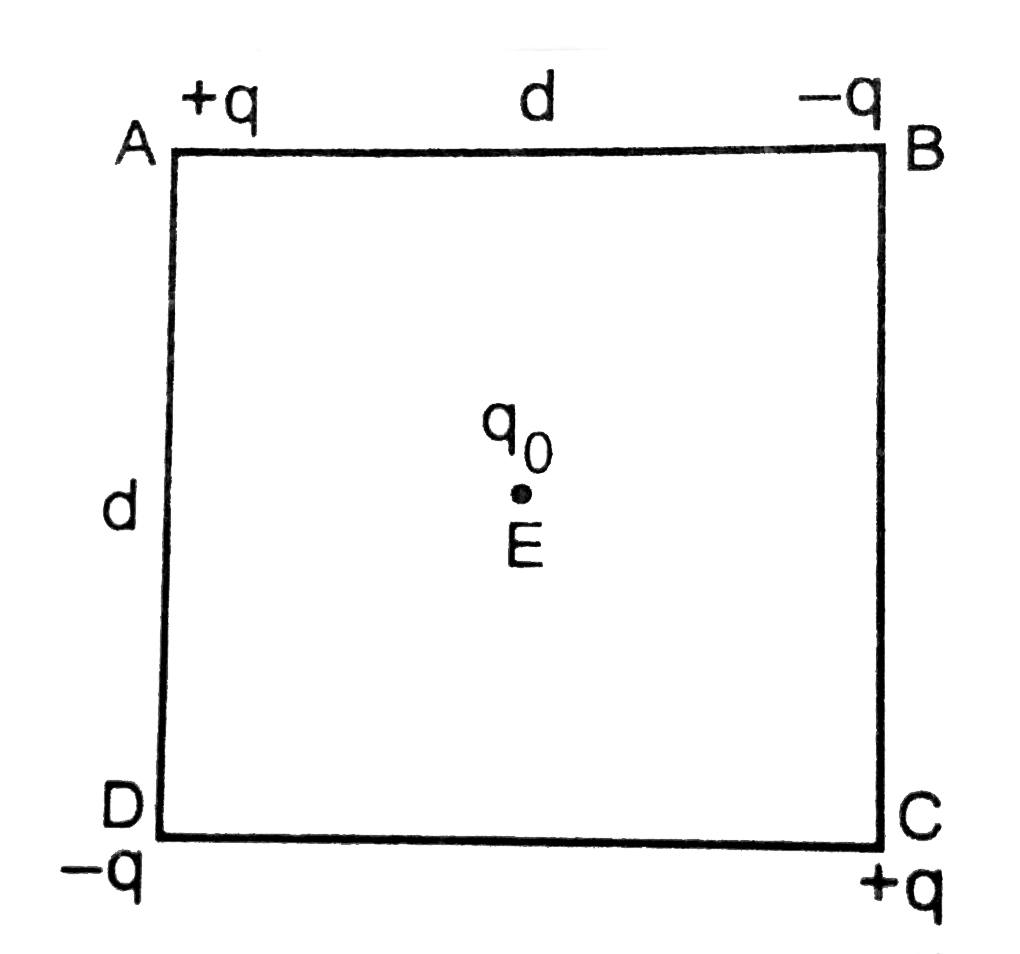
View SolutionFour charges are arranged at the corners of a square ABCD of side d, as shown in Fig. Find the work required to put together this arrangement
(b) A charge `q_(0)` brought to the center E of the square, the four charges being held fixed at the corners . How much extra work in needed to do this ?
View SolutionTwo electrons each moving with a velocity of `10^(6) ms^(-1)` are released towards eachother. What will be the closest distance of approach between them ?
View SolutionTwo identical particles of mass m carry a charge `Q`, each. Initially one is at rest on a smooth horizontal plane and the other is projected along the plane directly towards first particle from a large distance with speed v. The closest distance of approach be .
View SolutionAn electric dipole consists of two opposite charges of magnitude `2xx10^(-6)C`, separated by 4.0 cm. the dipole is placed in an external field of `10^(5)NC^(-1)` find the work done by an external agent to turn the dipole thorugh `180^(@)`
View SolutionA certain dipole has opposite charges of `2xx10^(-5)` separated by a distance of 0.2mm. It is placed in a uniform electric field of `10^(3)Vm^(-1).` (i) find the torque, the field exerts on the dipole when the dipole is at `60^(@)` with respect to the field. (ii) find the work, it would take to rotate the dipole to this position starting with the dipole aligned parallel to the field
View SolutionTwo charges `+3.2xx10^(-19)` and `-3.2xx10^(-19)C` placed at `2.4A` apart from an electric dipole. It is placed in a uniform electric field of intensity `4xx10^(5) "volt"//m`. The electric dipole moment is
View SolutionA uniform electric field of `200NC^-1` exists in space in the X-direction. Calculate the flux of this field through a plane square area of edge 10 cm placed in the Y-Z
View SolutionA circular plane sheet of radius 10 cm is placed in a uniform electric field of `5xx10^(5) NC^(-1)`, making an angle of `60^(@)` with the field. Calculate electric flux through the sheet.
View SolutionCalculate the total charge enclosed by a closed surface, the number of lines of force emerging from it is 15000 and that entering it is 5000.
View SolutionA spherical Gaussian surface encloses a charge of `8.85xx10^(-8) C` (i) Calculate the electric flux passing through the surface (ii) If the radius of Gaussian surface is doubled, how would the flux change ?
View SolutionAn arbitrary surface encloses a dipole. What is the electric flux through this surface ?
View SolutionA point charge of `10^(-7)`C is situated at the centre of a cube of side 1m. Calculate the electric flux through its surface.
View SolutionFind the electric flux through each face of a hollow cube of side 10 cm, if a charge of `8.85muC` is placed at its centre.
View SolutionConsider a uniform electric field `E = 3xx10^(3) hat(i) N//C`. (a) What is the flux of this field through a square of 10 cm on a side whose plane is parallel to the yz plane ? (b) What is the flux through the same square if the normal to its plane makes a `60^(@)` angle with the x-axis ?
View SolutionThe electric field in a region is given by `vecE=3/5 E_0veci+4/5E_0vecj` with `E_0=2.0 xx 10^3 N C^(-1)`. Find the flux of this field through a recatngular surface of area `0.2m^2` parallel to the y-z plane.
View SolutionA charge q is situated at the centre of an imaginary hemispherical surface, as shown in figure. Using gauss's theorem and symmetry considerations, determine the electric flux due to this charge through the hemisphere surface.
View Solution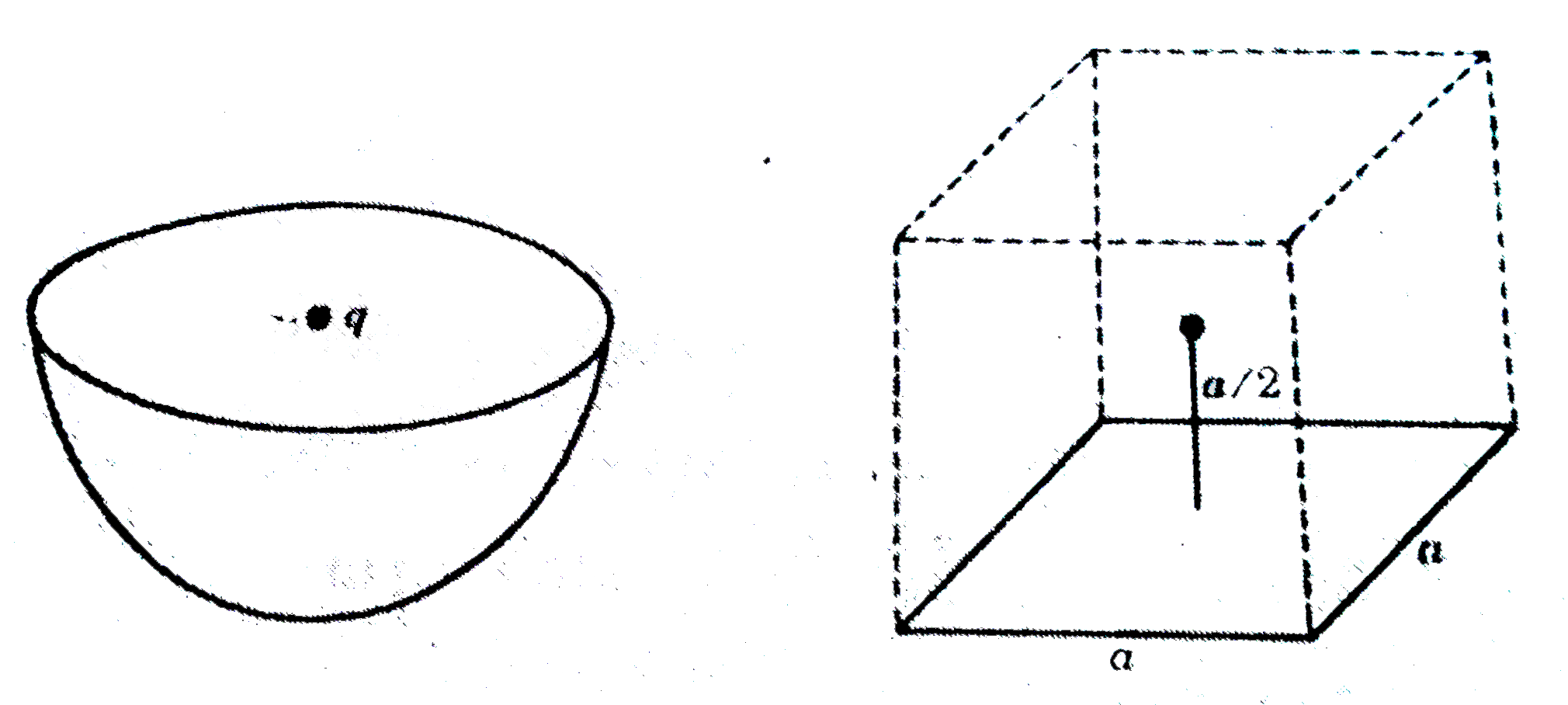
A point charge q is placed at a distnace a/2 directly above the centre of a square of side a, as shown figure. Find the magnitude of the electric flux through the square.
View SolutionThe electric components in the figure are `E_(x)=alphax^(1//2) ,E_(y)=0,E_(z)=0` where `alpha=800N//m^(2)` if `a=0.1m` is the side of cube then the charge with in the cube is
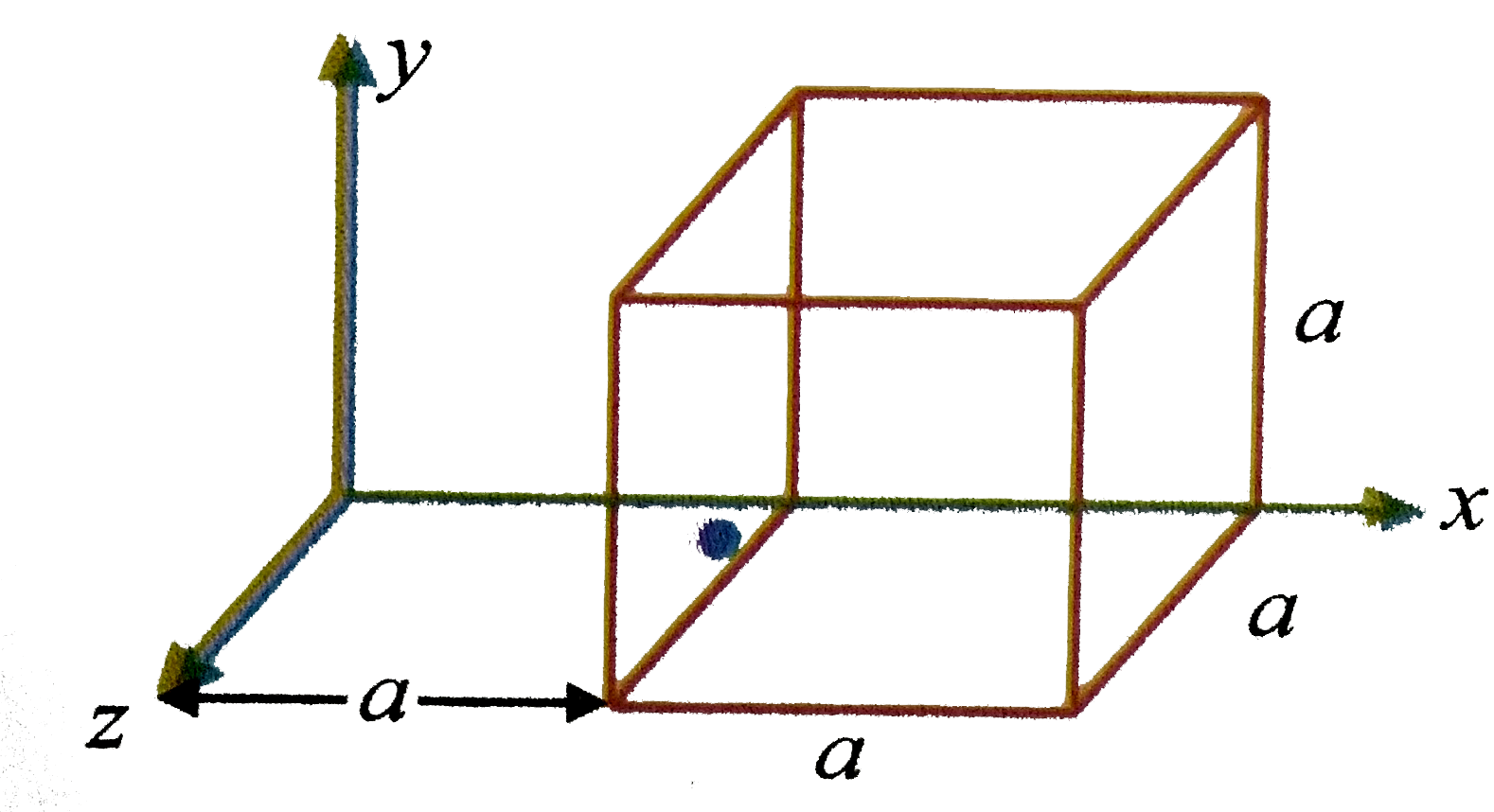
View SolutionThe electric field In a region is given gy `vecE=(E_(0)x)/(b)hati`. Find the charge contained in the cubical volume bounded by the surfaces x=0, x=a, y=0, y=a,z=0 and z=a. take `E_(0)=5xx10^(3)NC^(-1),a=1cm and b=2cm`.
View SolutionAn infinitely long wire is stretched horizontally 4 metre above the surface of the earth. It carries a charge `1muC` per cm of its length. Calculate its electric field at a point on the earth's surface vertically below the wire.
View SolutionTwo large metal plates each of area `1 m^(2)` are placed facing each other at a distance of 5 cm and carry equal and opposite charges on their faces. If the electric filed between the plates is `1000 NC^(-1)`, find the charge on each plate.
View SolutionA charge of 1500 `muC` is distributed uniformly over a very large sheet of surface area `300m^(2)`. Calculate the electric field at a distance of 25 cm.
View SolutionA uniformly charged sphere has a total charge of `300muC` and radius of 8 cm. find the electric field (i) at a point 16 cm from the centre of the sphere (ii) at a point on the surface of the sphere (iii) at a point inside the sphere.
View SolutionA charged particle having a charge of `-2.0 xx 10^(-6) C` is placed close to a non-conducting plate having a surface charge density `4.0 xx 10^(-6) C m^(-2)`. Find the force of attraction between the particle and the plate.
View Solution
Problems for self practive questions and complete solutions for chapter ELECTRIC POTENTIAL AND ELECTRIC FLUX of DHANPAT RAI & CO PHYSICS (HINGLISH) of Class 12