Complete Solutions to Example of chapter ELECTRIC POTENTIAL AND ELECTRIC FLUX of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTRIC POTENTIAL AND ELECTRIC FLUX |
| SL ARORA | Example |
| Number Of Questions | 59 |
| Academic Year | 2023-24 |
The work done in moving a charge of 3 C between two points is 6J. What is the potential difference between the two points?
View SolutionDetermine the electric potential at the surface of a gold nucleus. The radius is `6*6xx10^(-15) m` and the atomic number `Z = 79`. Given charge on proton `1.6xx10^(-19) C`.
View SolutionThe electric potential at 0.9m from a point charge is `+50 V`. What is the magnitude and sign of the charge ?
View SolutionA metal wire is bent in a circle of radius 10 cm. It is given a charge `200 muC` which is spread on it uniformly. Calculate the electric potential at its center.
View SolutionThe electric field at a point due to a point charge is `20 NC^(-1)` and electric potential at that point is `10 JC^(-1)`. Calculate the distance of the point from the charge and the magnitude of the charge.
View SolutionTo what potential we must charge an insulate sphere of radius 14 cm, so that the surface charge density is equal to `2 muC m^(-2)` ?
View SolutionA charge of `24 muC ` is given to a hollow metallic sphere of radius 0.2m. Find the potential
(i) at the surface of sphere
(ii) at a distance of 0.1 cm from the center of sphere.
View SolutionTwenty seven drops of mercury are charged simultaneously to the same potential of 10V. What will be the potential if all the charge drops are made to combine to form one large drop? Assume the drops to be spherical.
View SolutionTwo points A and B located in diametrically opposite directions of a point charge of +2`muC` at distances 2.0 m and 1.0 m respectively from it. Determine the potential difference `V_(A)-V_(B)`
View SolutionTwo charges `3xx10^(-8) C and -2xx10^(-8)C ` are located 15 cm apart. At what point on the line joining the two charges is the electric potential zero ? Take the potential at infinity to be zero.
View SolutionFind the potential at centre of square having charges `2xx10^(-9)C,+1xx10^(-9)C,-2xx10^(-9)C and 3xx10^(-9)C` at the four corners. The side of the square is `sqrt(2)m`.
View SolutionA cube of side b has a charge q at each of its vertices. Determine the potential and electric field due to this charge array at the center of the cube.
View SolutionA regular hexagon of side 10 cm has a charge `5 muC` at each of its vertices. Calculate the potential at the center of the hexagon.
View SolutionTwo tiny spheres carrying charges `1.5 muC` and `2.5 muC` are located 30 cm apart. Find the potential
(a) at the mid-point of the line joining the two charges and
(b). At a point 10 cm from this mid-point in a plane normal to the line and passing through the mid-point.
View SolutionAn electric field is set up by two point charges of `+1.2xx10^(-8)C and -1.2xx10^(-8)C` as shown in fig. find the potentials at the point A,B, and C
View SolutionA charge of 8 mC is located at the origin. Calculate the work done in taking a small charge of `-2xx10^(-9)` from a point P(0,0,3cm) to a point Q (0,4cm,0) via a point R(0,6cm,9cm).
View SolutionFour charges `+q, +q, -q, and -q` are placed, respectively, at the corners `A,B,C, and D` of a square of side `a`, arranged in the given order. `E and F` are the midpoints of sides `BC and CD`, respectively, `O` is the center of square.
The work done in carrying a charge `e` from `O` to E is.
View Solution`ABC` is a right - angled triangle, where `AB and BC` are `25 cm and 60 cm`, respectively. A metal sphere of `2 cm` radius charged to a potential of `9 xx 10^5 V` is placed at `B` as in (Fig. 3.133). Find the amount of work done in carrying a positive charge of 1 coulomb from C to A.
 .
.
View SolutionFig shows a charge array known as an 'electric quadrupole'. For a point on the axis of the quadrupole, obtain the dependence of potential on r for `r//a gtgt 1`, and contract your results with that due to an electric dipole and an electric monopole (i.e, a single charge).
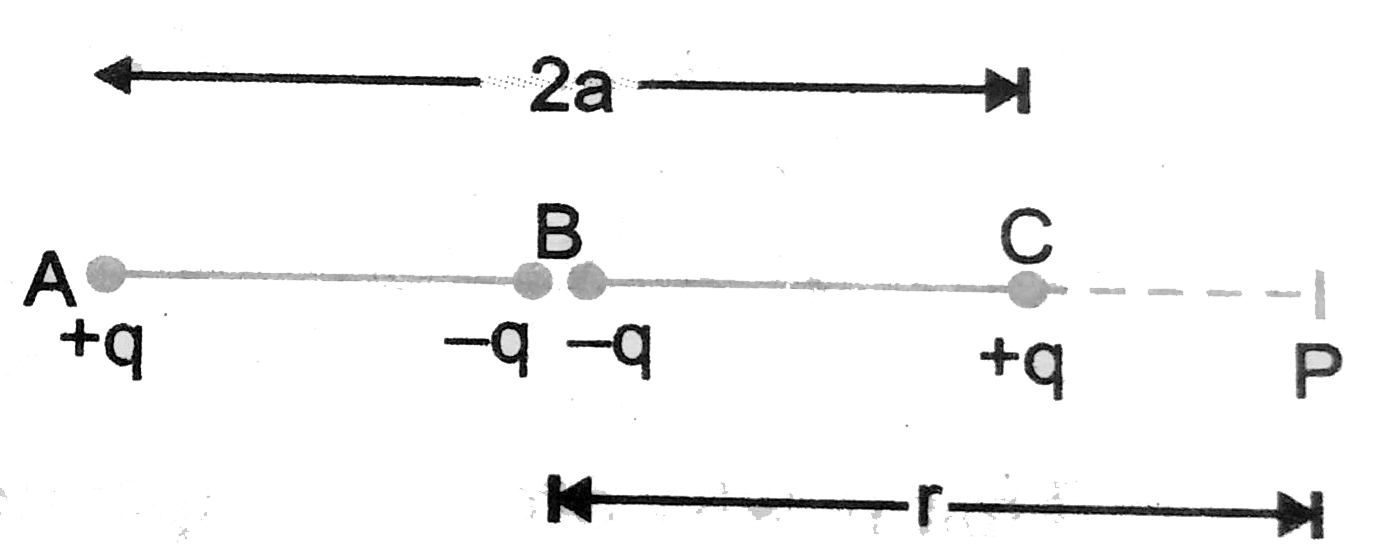
View SolutionA short electric dipole has dipole moment of `4xx10^(-9)Cm`. Determine the electric potential due to the dipole at a point distant 0.3 m from the centre of the dipole situated on (a) the axial line (b) on equatorial line and (c) on a line making an angle of `60^(@)` wth the dipole axis.
View SolutionTwo point charges of `+3muC` are placed `2xx10^(-3)`m apart from each other. Calculate (i) electric field and electric potential at a distance of 0.6m from the dipole in broad-side-on position (ii) electric field and electric potential at the same point after rotating the dipole through `90^(@)`.
View SolutionFind the electric field between two metal plates 3 mm- apart connected to 12 V battery.
View SolutionCalculate the voltage needed to balance on all drop carrying 10 electrons when located between the plates of a capacitor which are 5 mm apart. Mass of oil drop is `3xx10^(-16) kg `(take `g = 10m//s^(2))`
View SolutionA spark passes though air when the potential gradient is `3xx10^(6)` volts per metre what must be the radious of an isoated metal sphere which can be changed to a potentiial of 3 million voilts before there are sparks in the air?
`["Hint":E= (Q)/(4piepsi_(0)r^(2))and V=(Q)/(4piepsi_(o)r), thereforeE=(V)/(r)]`
View SolutionIf the potentail in the region of space around the point `(-1m,2m,3m)` is given by `V = (10 x^(2) + 5 y^(2) - 3 z^(2))`, calculate the three components of electric field at this point.
View SolutionThe electric field outside a charged long straight wire is given by `E = (1000)/(r ) V m^(-1)`, and is directed outwards. What is the sign of the charge on the wire ? If two points `A` and `B` are situated such that `r_(A) = 0.2 m` and `r_(B) = 0.4 m`, find the value of `(V_(B) - V_(A))`.
View Solution(a). Determine the potential energy of a system containing two charges `7muC` and `-2muC` separated by a distance 18 cm. (b) How much work is needed to separate the two charges infinitely away from each other?
View SolutionTwo positive point charges of `0.2 muC and 0.01 muC` are placed 10 cm apart. Calculate the work done in reducing the distance to 5 cm.
View SolutionTwo identical particles, each having a charge of `2.0xx10^(-4) C` and then released. What would be the speeds of the particles when the separtion becomes large?
View SolutionTwo particles have equal masses of 5.0 g each and opposite charges of `+4.0 xx10^(-5) C.` They are released from rest with a separation of 1.0 m between them. Find the speeds of the particles when the separation is reducced to 50 cm.
View SolutionIf one of the two electrons of a hydrogen molecule is removed, we get a hydrogen molecule ion `(H_(2)^(+))`. In the ground state of `H_(2)^(+)`, the two protons are separated roughly by `1.5 Å` and electron is roughly `1 Å` from each proton. Determine the potential energy of the system. Specify your choice of zero of potential energy.
View SolutionFour charges are arranged at the corners of a square ABCD of side d, as shown in Fig. Find the work required to put together this arrangement
(b) A charge `q_(0)` brought to the center E of the square, the four charges being held fixed at the corners . How much extra work in needed to do this ?
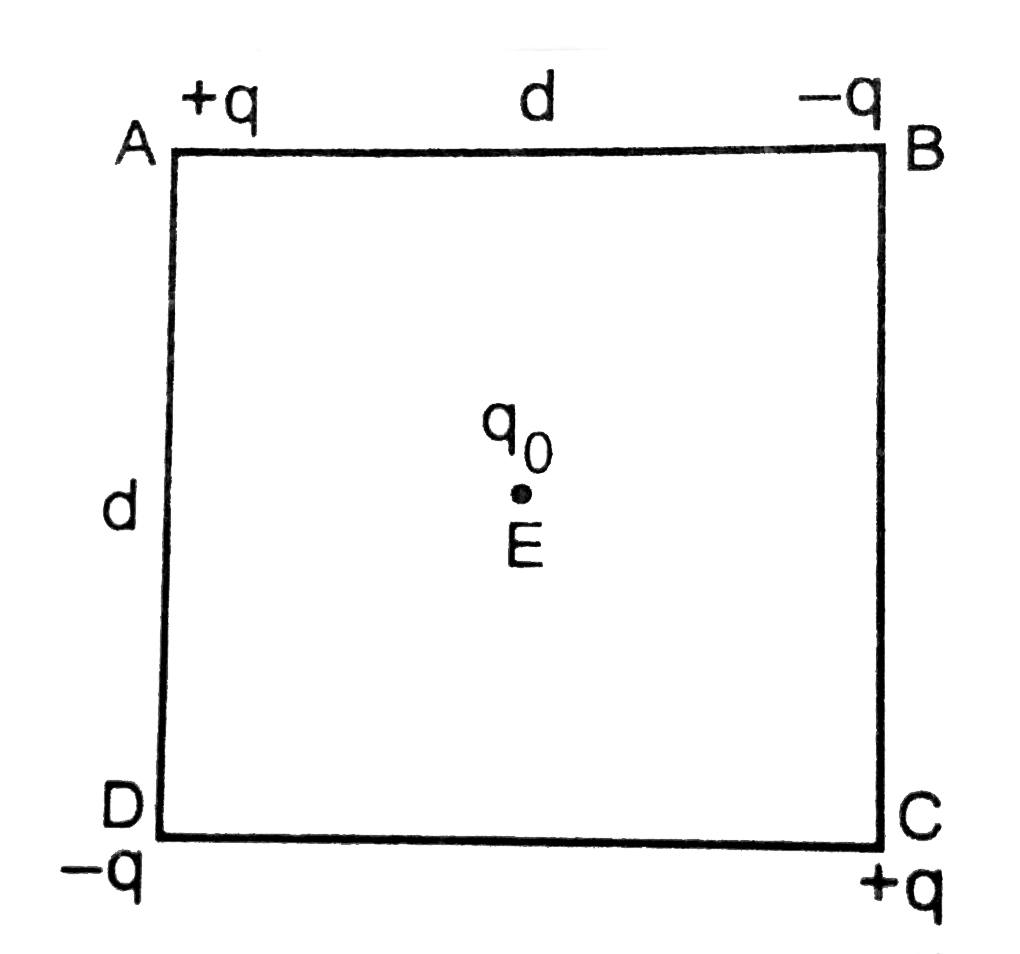
View SolutionTwo charges `q_(1)=+2xx10^(-8)C and q_(3)=-0.4xx10^(-8)C` are placed 60cm apart, as shown in fig. A third charge `q_(3)=+0.2xx10^(-8)C` is moved along the arc of a circle of radius 80 cm from C to D. Compute the percentage change in the energy of the system.
View SolutionAn electric dipole of length 2 cm is placed with its axis making an angle of `60^(@)` to a uniform electric field of `10^(5)NC^(-1)` if its experiences a torque is `8sqrt(3)`Nm, calculate the
(i). Magnitude of the charge on the dipole and
(ii). potential energy of the dipole.
View SolutionAn electric dipole consists of two opposite charges each of magnitude `1 muC` separated by `2 cm`. The dipole is placed in an external uniform field of `10^5 NC^-1` intensity. Find the
a. maximum torque exterted by the field on the dipole, and
b. work done in roating the dipole through `180^(@)` starting from the position `theta = 0^(@)`.
View SolutionThe electric dipoles of moments `p_(1) and p_(2)` are in a straight line. Show that the potential energy of each in the presence of the other is `-(1)/(2piepsi_(0))*(p_(1)p_(2))/(r^(3))`, where r is the distance between the dipoles. (Assume r to be much greater than the length of the dipole).
View SolutionA molecule of a substance has a permanent electric dipole moment of magnitude `10^(-29) `C m. A mole of this substance is polarized at low temperature by appling a strong elecrostatic field of magnitude `10^(6) V m^(-1)`. The direction of the field is suddenly changed by an angle of `60^(@)`. Estimate the heat released by the substance in aligning its dipole along the new direction of the field. For simplicity, assume `100%` polarisation of sample.
View SolutionIn a region of space, the electric field is given by `vecE = 8hati + 4hatj + 3hatk`. The electric flux through a surface of area 100 units in the xy plane is
View SolutionConsider a uniform electric field `E = 3xx10^(3) hat(i) N//C`. (a) What is the flux of this field through a square of 10 cm on a side whose plane is parallel to the yz plane ? (b) What is the flux through the same square if the normal to its plane makes a `60^(@)` angle with the x-axis ?
View SolutionA circular plane sheet of radius 10 cm is placed in a uniform electric field of `5xx10^(5) NC^(-1)`, making an angle of `60^(@)` with the field. Calculate electric flux through the sheet.
View SolutionA positive charge of `17.7 muC` is placed at the centre of a hollow sphere of radius `0.5m`. Calculate the flux density through the surface of the sphere.
View SolutionFive thousand lines of force enter a certain volume of space and three thousand lines emerge from it. What is the total charge in coulomb within this volume ?
View SolutionA point charge causes an electric flux of `-1.0xx10^(3) N m^(2)//C` to pass through a spherical Gaussian surface of 10.0 cm radius centred on the charge. (a) If the radius of the Gaussian surface were doubled, how much flux would pass through the surface ? (b) What is the is the value of the point charge ?
View SolutionCareful measurement of the electric field at the surface of a black box indicates that the net outward flux through the surface of the box is `8.0xx10^(3) Nm^(2)//C` (a) what is the net charge inside the box ? (b) If the net outward flux through the surface of the box were zero, could you conclude that there were no charges inside the box ? Why or why not?
View SolutionA point charge `+10 mu C` is at distance of 5cm directly above the center of a square of side 10 cm as shown in Fig. What is the magnitude of the electric flux through the square ? (Hint. Think of the square of the square as one face of a cube with edge 10 cm)
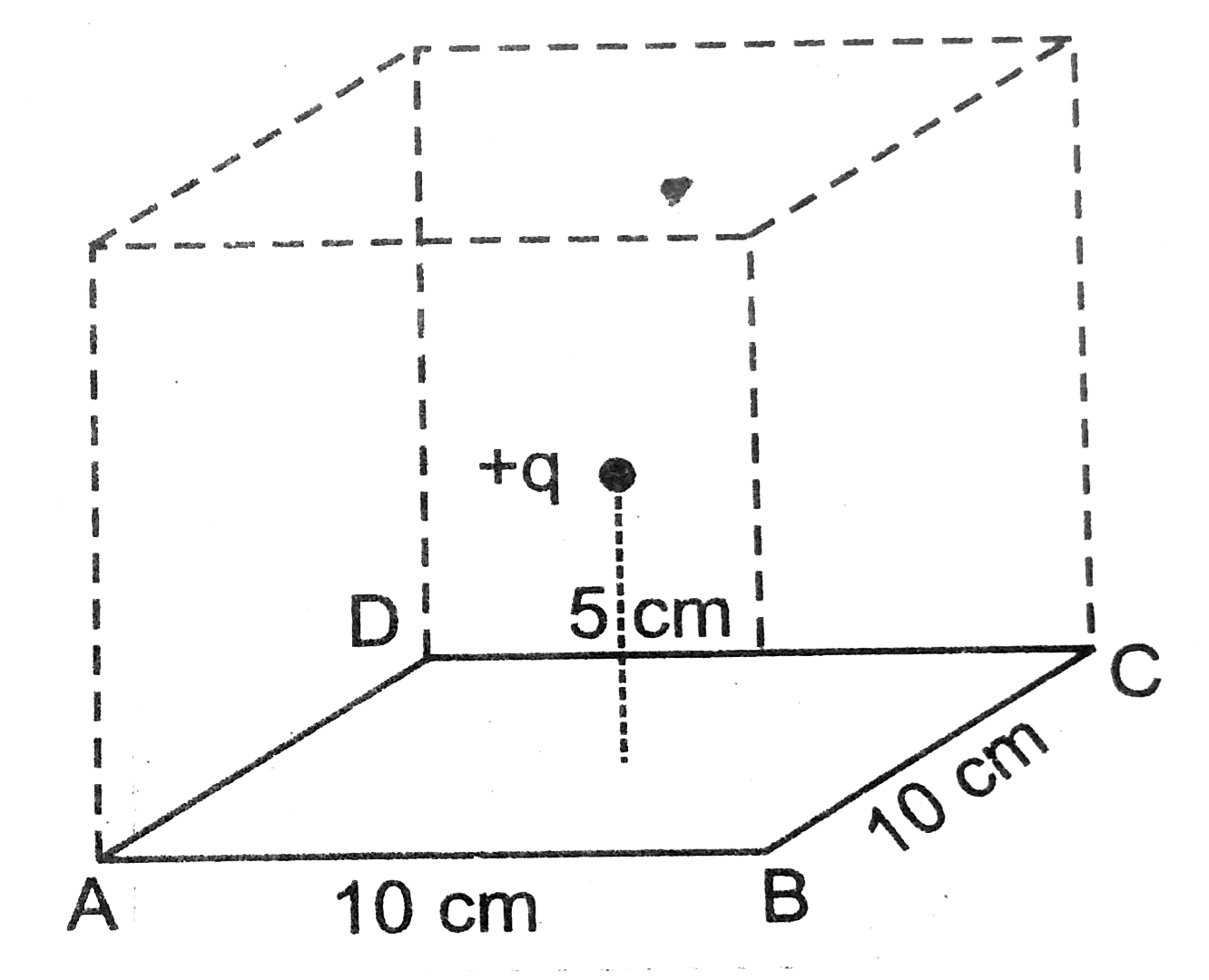
View SolutionA uniformly charged conducting sphere of 2.4m diameter has a surface density of `80.0 mu C//m^(2)`. (a) Find the charge on the sphere (b) What is the total electric flux leaving the surface of the sphere ?
View SolutionAn electric charge is placed at the centre of a cube of side `a`.The electric flux
(i) through one of its faces `(q)/(6 in_(0))`
through one of its faces `(q)/(3 in_(0))`
(iii) through all of its faces `(q)/(in_(0))`
(iv) through one of its faces `(q)/(2 in_(0))`
View SolutionA sphere `S_(1)` of radius `r_(1)` encloses a total charge Q. If there is another concentric sphere `S_(2)` of radius `r_(2) (gt r_(1))` and there be no additional charges between `S_(1) and S_(2)` find the ratio of electric flux through `S_(1) and S_(2)`,
View SolutionThe electric components in the figure are `E_(x)=alphax^(1//2) ,E_(y)=0,E_(z)=0` where `alpha=800N//m^(2)` if `a=0.1m` is the side of cube then the charge with in the cube is
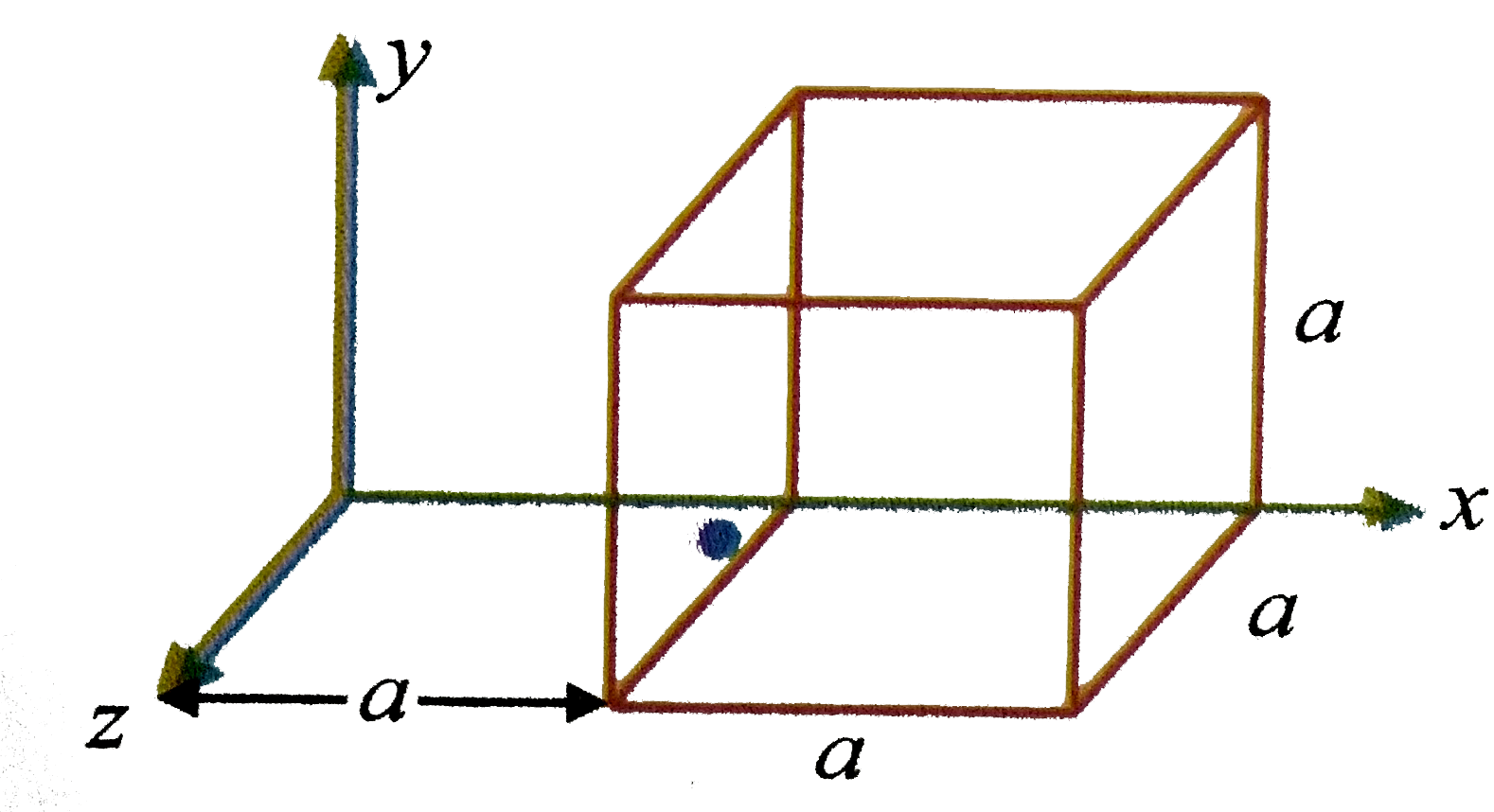
View SolutionA uniform electric field exists in space. Find the flux of this field through a cylindrical surface with the axis parallel to the field.
View SolutionA charge `q_0` is distributed uniformly on a ring of radius R. A sphere of equal radius R constructed with its centre on the circumference of the ring. Find the electric flux through the surface of the sphere.
View SolutionA cylinder of large length carries a charge of `2xx10^(-8)Cm^(-1)` find the electric field at a distance of 0.2 m from it.
View SolutionAn infinite line charge produces a field of `9xx10^(-4)N" "C^(-1)` at a distance of 2 cm. calculate the linear charge density.
View SolutionIf the field near the earth's surface is 300V `m^(-1)` directed downwards , what is the surface density of change on the surface of the earth?
View SolutionTwo large, thin metal plates are parallel and close to each other. On their inner faces, the plates have surface charge densities of opposite signs and of magnitude `19xx10^(-22) Cm^(-2)`.
What is E (a) to the left of the plates (b) to the right of the plates (c) between the plates ?
Here, `sigma = 19xx10^(-22) Cm^(-2)`
View SolutionAn infinite plane sheet of charge density `10^(-8) Cm^(-2)` is held in air. In this situation how far apart are two equipotenitial surfaces, whose p.d is 5 V ?
View SolutionA conducting sphere fo radius 10 cm has an unknown charge. If the electric field 20 cm from the center of the sphere is `1.5xx10^(3) N//C` and points radilly inwards, what is the net charge on the sphere ?
View SolutionA spherical conductor of radius 12 cm has a charge of `1.6xx10^(-7)C` distributed uniformly on its surface. What is the electric field (a) inside the sphere (b) just outside the sphere (c ) at a point 18 cm from the center of the sphere ?
View SolutionIn a van de Graaff type generator, a spherical metal shell is to be a `15xx10^(5)V` electrode. The dielectric strength of the gas surrounding the electrode is `5xx10^(7)Vm^(-1)`. What is the minimum radius of the spherical shell required?
View Solution
Example questions and complete solutions for chapter ELECTRIC POTENTIAL AND ELECTRIC FLUX of DHANPAT RAI & CO PHYSICS (HINGLISH) of Class 12