Complete Solutions to Problems For Self of chapter CURRENT ELECTRICITY of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | CURRENT ELECTRICITY |
| SL ARORA | Problems For Self |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
One billion electrons pass from a point P towards another point Q in `10^(-3)` s. What is the current in ampere ? What is its direction ?
View SolutionCalculate the number of free electrons passing through the filament of an electric lamp in one hour when the current through the filament is 0.32 A.
View SolutionIn the electrolysis of silver chloride, a charge of `4xx10^(5)` C is flowing through the electrolyte. Calculate the number of silver `(Ag^(+))` ions flowing through it.
View SolutionIn a hydrogen atom, the electron makes about `0.6xx10^(16)` revolutions per second around the nucleus. Determine the average current at any point on the orbit of the electron.
View SolutionAn electron gun emits `2.0xx10^(16)` electrons per second. What is the associated current ?
View SolutionAn electric current of `2.0 mu A` exists in a discharge tube. How much charge flows across a cross-section of the tube in 5 minutes ?
View SolutionAn electron moves in a circular orbit of radius 10 cm with a constant speed of `4.0xx10^(6) ms^(-1)`. Determine the electric current at a point on the orbit.
View SolutionThe current through a wire depends on time as `I=I_(0)+alpha t`, where `I_(0)=10` A and `alpha=4 As^(-1)`. Find the charge that flows across a section of the wire in 10 seconds.
View SolutionA current of 4.8 A is flowing in a copper wire of cross-sectional area `3xx10^(-4) m^(2)`. Find the current density in the wire.
View SolutionA voltage of 30 V is applied across a colour coded carbon resistor with first, second and third rings of blue, black and yellow colurs. What is the current flowing through the resistor ?
View SolutionThe sequence of bands marked on a carbon resistor is yellow , red orange and silver. What is its (a) resistance and (b) tolerance ?
View SolutionThe resistance of a conductivity wire of length 1.1 m and of diameter 0.14 mm is `30 Omega`. Calculate its resistivity.
View SolutionA metal wire of specific resistance `64xx10^(-6) Omega` m and length 1.98 cm has a resistance of `7 Omega`. Find its radius.
View SolutionA negligbly small current is passed through a wire of length 15 cm and uniform cross-section `6.0xx10^(-7) m^(2)` and its resistance is measured to be `5.0 Omega`. What is the resistivity of the material at the temperature of the experiment ?
View SolutionCalculate the resistance of a 2 m long nichrome wire of radius 0.321 mm. Resistivity of nichrome is `15xx10^(-6) Omega` m. If a potential difference of 10 V is applied across this wire, what will be the current in the wire ?
View SolutionFind the resistance of a hollow cylindrical conductor of length 1.0m and inner and outer radii 1.0mm and 2.0mm respectively. The resistivity of the material is `2.0xx10^(-8)(Omega)m`.
View SolutionCalculate the electric field in a copper wire of cross-sectional area `2.0 mm^(2)` carrying a current of 1 A. The resistivity of copper `=1.7xx10^(-8) Omega`m.
View SolutionA given copper wire of resistance R is stretched to reduce its diameter to half its previous value. What sould be its new resistance ?
View SolutionWhat will be the change in resistance of a constantan wire when its radius is made half and length reduced to one-fourth of its original length ?
View SolutionA wire of resistance `10 Omega` is drawn out so that its length is thrice its original length. Calculate its new resistance (resistivity and density of the material remain uncharged).
View SolutionA metallic wire of length 1 m is stretched to duble its length. Calculate the ratio of its initial and final resistances assuming that there is no change in its density on stretching.
View SolutionA cylindrical wire is stretched to increase its length by 10%. Calculate the percentage increase in resistance.
View SolutionTwo copper wires A and B of equal masses are taken. The length of A is double the length of B. If the resistance of wire A is `160 Omega `, then calculate the resistance of the wire B.
View Solution`1kg` piece of copper is drawn into a wire `1mm` thick and another piece into a wire `2mm` thick. Compare the resistance of these wires.
View SolutionA rheostat has 100 turns of a wire of radius 0.4 mm having resistivity `4.2xx10^(-7) Omega`m. The diameter of each turn is 3 cm. What is the maximum value of resistance that it can introduce ?
View SolutionCalculate the conductivity of a wire of length 2 m, area of cross-sectionl `2 cm^(2)` and resistance `10^(-4) Omega`.
View SolutionWhat length of a wire of diameter 0.46 mm and specific resistance `50xx10^(-6) Omega`m would be required to make a coil of resistance `10 Omega` ?
View SolutionThe size of a carbon block is `1.0xx10 cm xx50 cm`. Find its resistance (i) between the opposite square faces (ii) between the opposite rectangular faces of the block. The resistivity of carbon is `3.5xx10^(-5) Omega cm`.
View SolutionGiven that resistivity of copper is `1.68xx10^(-8) Omega`m. Calculate the amount of copper required to draw a wire 10 km long having resistance of `10 Omega`. The density of copper is `8.9xx10^(3) kg m^(-3)`.
View SolutionA potential difference of 10 V is applied across a conductor of resistance `1 k Omega`. Find the number of electrons flowing through the conductor in 5 minutes.
View SolutionA wire of resistance `48 Omega` is uniformly stretched until its new length becomes 4 times the original length. Find its new resistance.
View SolutionTwo wires A and B of the same material have their lengths in the ratio `1 : 5` and diameters in the ratio ` 3 : 2`. If the resistance of the wire B is `180 Omega`, find the resistance of the wire A.
View SolutionTwo wires of the same material have resistances in the ratio ` 16 : 81` and lengths in the ratio ` 1 : 4`. Compare their radii of cross-section.
View SolutionTwo wires of different materials have resistances in the ratio `4 : 3`, lengths in the ratio `2 : 1` but have same radii of cross-section. Compare their resistivities.
View SolutionA uniform wire is cut into four segments. Each segment is twice as long as the earlier segment. If the shortest segment has a resistance of `4 Omega`, find the resistance of the original wire.
View SolutionThe free electrons of a copper wire of cross-sectional area `10^(-6) m^(2)` acquire a drift velocity of `10^(-4) m//s` when a certain potential difference is applied across the wire. Find the current flowing in the wire if the density of free electrons in copper is `8.5xx10^(28) "electrons"//m^(3)`.
View SolutionWhat is the drift velocity of electrons in a copper conductor having a cross-sectional area of `5xx10^(-6) m^(2)` if the current is 10 A. Assume there are `8.0xx10^(28) "electrons"//m^(3)`.
View SolutionCalculate the drift velocity for the electrons in a silver wire which has a radius of 0.1 cm and carries a current of 2 A. Atomic mass of silver=108 and density of silver `=10.5xx10^(3) kg//m^(3)`.
View SolutionA current of 2 A is flowing through a wire of length 4 m and cross-sectional area `1 mm^(2)`. If each cubic metre of the wire contains `10^(29)` free electrons, find the average time taken by an electron to cross the length of the wire.
View SolutionA 10 C of charge flows through a wire in 5 minutes. The radius of the wire is 1 mm. It contains `5xx10^(22)` electrons per `"centimetre"^(3)`. Calculate the current and drift velocity.
View SolutionA copper wire of diameter 0.16 cm is connected in series to an aluminium wire of diameter 0.25 cm. A current of 10 A is passed through them. Find (i) current density in the copper wire (ii) drift velocity of free electrons in the aluminium wire. The number of free electrons per unit volume of aluminium wire is `10^(29) m^(-3)`.
View SolutionA current of 30 ampere is flowing through a wire of cross-sectional area `2 mm^(2)`. Calculate the drit velocity of electrons. Assuming the temperature of the wire to be `27^(@)C`, also calculate the rms velocity at this temperature. Which velocity is larger ? Given that Boltzman's constant `=1.38xx10^(-23) J K^(-1)`, density of copper `8.9 g cm^(-3)`, atomic mass of copper =63.
View SolutionWhat is the drift velcity of electrons in silver wire of length 1 m having cross-sectional area `3.14xx10^(-6)m^(2)` and carrying a current of 10 A . Given atomic mass of silver =108, density of silver `=10.5xx10^(3) kg m^(-3)`, charge on electron `=1.6xx10^(-19) C` and Avogadro's number `=6.023xx10^(26)` per kt-atom.
View SolutionFind the time of relaxation between collsion and free path of electrons in copper at room temperature. Given resistivity of copper`=1.7xx10^(-8) Omega`m, number density of electrons in copper `=8.5xx10^(28) m^(-3)`, charge on electron`=1.6xx10^(-19)` C, mass of electron `=9.1xx10^(-3)` kg and drift velocity of free electrons`=1.6xx10^(-4) ms^(-1)`
View SolutionA plantinum wire has resistance of `10 Omega` at `0^(@)C` and `20 Omega` at `273^(@)C`. Find the value of coefficient of resistance.
View SolutionA platinum resistance thermometer makes use of the variation of a conductor with temperature. If the resistance of this thermometer is `5 Omega " at " 20^(@)C " and " 16 Omega` when inserted in a furnace, find the temperature of the furnace. Given `alpha` for the platinum `=0.0036^(@)C`.
View SolutionThe temperature coefficent of resistance of a wire is 0.00125 per `.^(@)C`, At 300 K, its resistance is `1Omega`. At what temperature will its resistance become `2 Omega` ?
View SolutionAn electric toaster uses nichrome for its heating element. When a negligibly small current passes through it. It resistance at room temperature `(27.0^@C)` is found to be `75.3Omega`. When the toaster is connected to a `230 V` supply, the current settles, after a few seconds, to a steady value of `2.68 A`. What is steady temperature of the nichrome element? The temperature coefficient of resistance of nichrome averaged over the temperature range involved , `1.70xx10^-4C^-1`
View SolutionA nichrome heating element connected to a 200 V supply draws an intial current of 2.2 A which settles down after a few seconds to a steady value of 2.0 A. Find the steady temperature of the heating element. The room temperature is `30^(@)C` and the average temperature coefficient of resistance of nichrome is `1.7xx10^(-4) "per"^(@)C`.
View SolutionA standard coil marked `3 Omega` is found to have a true resistance of `3.115 Omega` at 300 K. Calculate the temperature at which marking is correct. Temperature coefficient of resistance of the material of the coil is `4.2xx10^(-3) .^(@)C^(-1)`.
View SolutionThe resistance of a silver wire at `0^(@)C " is " 1.25 Omega`. Upto what temperature it must be heated so that its resistance is doubled ? The temperature coefficient of resistance of silver is `0.00375^(@)C^(-1)`. Will the temperature be same for all silver conductors of all shapes ?
View SolutionThe resistance of a coil used in a platinum-resistance thermometer at `0^(@)C` is `3.00 Omega` and at `100^(@)C` is `3.75 Omega`. Its resistance at an unkown temperature is measured as `3.15 Omega`. Calculate the unknown temperature.
View SolutionThe temperature coefficient of a resistance wire is `0.00 12^(@)C^(-1)`. At 300 K, its resistance is `1 Omega`. At what temperature the resistance of the wire will be `2 Omega` ?
View SolutionThe temperature coefficient of copper is `0.004^(@)C^(-1)`. Find the resistance of a 5 m long copper wire of diameter 0.2 mm at `100^(@)C`, if the resistivity of copper at `0^(@)C` is `1.7xx10^(-8) Omega` m.
View SolutionThree resistors of `1 Omega, 2 Omega " and " 3 Omega` are combined in series. (i) What is the total resistance of the combination ? (ii) If the combination is connected to a battery of emf 12 V and negligible internal resistance, obtain the potential dropo across each resistor.
View Solution(i) Three resistors `2 Omega, 4 Omega " and " 5 Omega` are comined in parallel. What is the total resistance of the combination ? (ii) If the comnbination is connected to a battery of 20 V and negligible internal resistance, determine the current through each resistor, and the total current drawn.
View SolutionHow can the resistances of `2Omega, 3 Omega " and " 6 Omega` be connected to give an effective resistance of `4 Omega` ?
View SolutionGiven three resistances of `30 Omega` each. How can they be connected to given a total resistance of (i) `90 Omega (ii) 10 Omega (iii) 45 Omega` ?
View SolutionA `5 Omega` resistor is connected in series with a parallel combination of n resistors of `6 Omega` each. The equivalent resistance is `7 Omega`. Find n.
View SolutionA uniform wire which connected in parallel with the 2 m long wire, will give a resistance of `2.0 Omega`.
View SolutionThe resistance of two conductors in series is `18 Omega` and the resistance becomes `4 Omega` when connected in parallel. Find the resistance of individual conductors.
View SolutionA wire whose resistance is 90 ohm is cut into 3 pieces of equal lengths which are then arranged in parallel. Calculate the resistance of the combination.
View SolutionWhen a current of 0.5 A is passed through two resistances in series, the potential difference between the ends of the series arrangement is 12.5 V. On connecting them in parallel and passing a current of 1.5 A, the potential difference between their ends is 6 V. Calculate the two resistances.
View SolutionTwo wires a and b, each of length 40 m and area of cross-section `10^(-7) m^(2)` , are connected in series and a potenital difference of 60 V is applied between the ends of this combined wire. Their resistances are respectively 40 and `20 Omega`. Determine for each wire (i) specific resistance, (ii) electric-field and (iii) current-dentsity.
View SolutionCalculate the equivalent resistance between points A and B in each of the following networks of resistors :

View SolutionCalculate the resistance between points A and B for the following networks :


View SolutionFind the equivalent resistance of the networks shown in Fig. 4.51 between the points A and B.

View SolutionFind the potential difference between the points A and B for the network shown in Fig. 4.52.

View SolutionIn the circuit diagram shown in Fig. 4.53, a voltmeter reads 30 V when connected across `400 Omega` resistance. Calculate what the same voltmeter reads when it is connected across `300 Omega` resistance.
View SolutionFind the potential difference between points A and B `(V_(B)-V_(A))` in the network
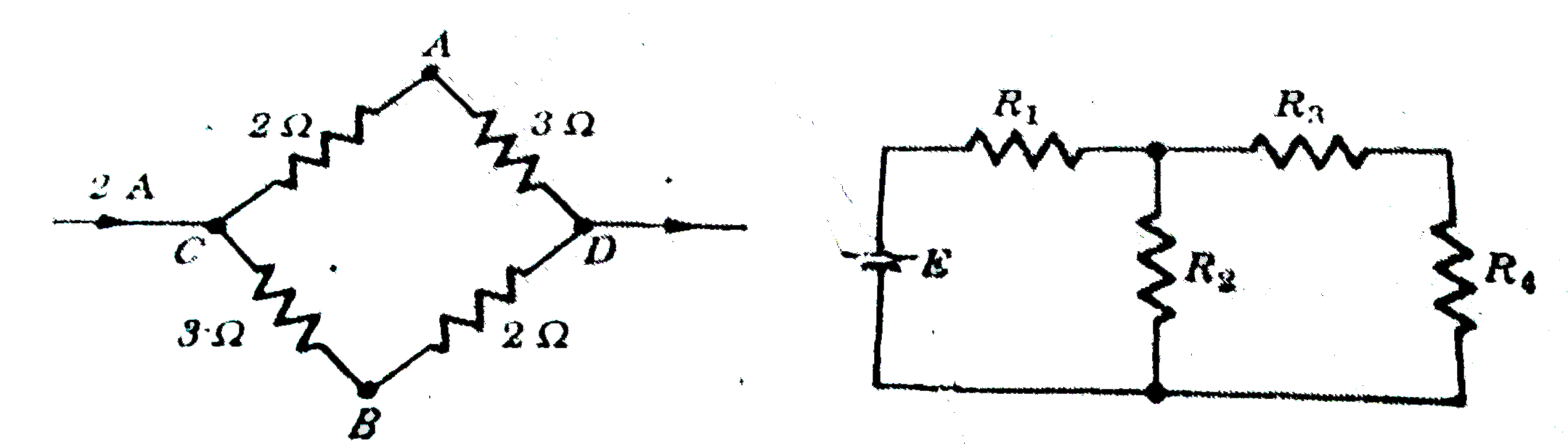
View SolutionDetermine the voltage drop across the resistance `R_(1)` in the circuit given in Fig. 4.55 with `epsilon=90 V, R_(1)=5 k Omega, R_(2)=5k Omega, R_(3)=10 k Omega " and " R_(4)=10 k Omega`.
View SolutionFind the equivent resistance between points A and B

View SolutionLetter A as shown in Fig. 4.57 has resistance on each side of arm. Calculate the total resistance between two ends of the legs.
View SolutionFind the resistance between the points (i) A and B and (ii) A and C of the network
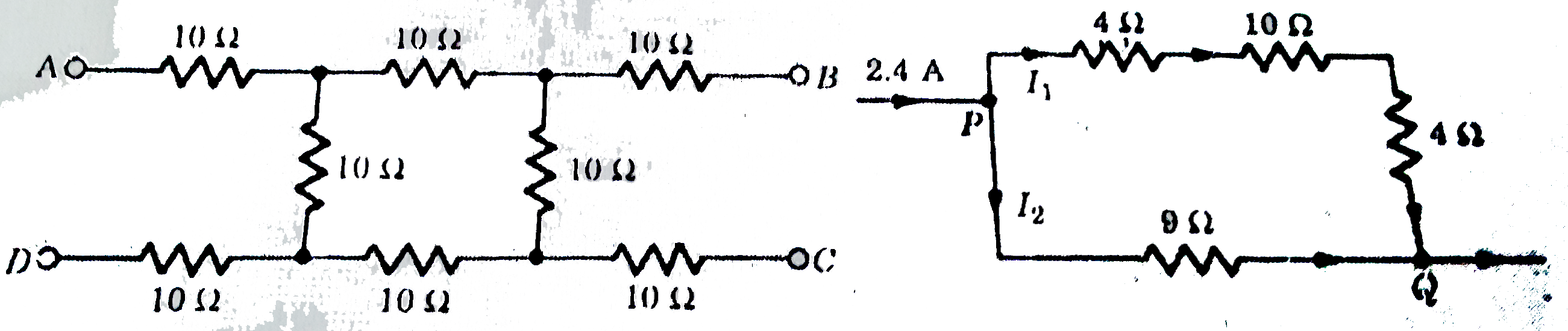
View SolutionA combination of four resistances is shown in Fig. 4.59. Calculate the potential difference between the points P and Q, and the values of currents flowing in the different resistances.
View SolutionFind the equivalent resistance of the circuit shown in Fig.4.60 between the points A and B. Each resistor has a resistance r.

View SolutionFind the equivealent resistance of the circuit shown in Fig. 4.61 between the points P and Q. Each resistor has a resistance r.
View Solution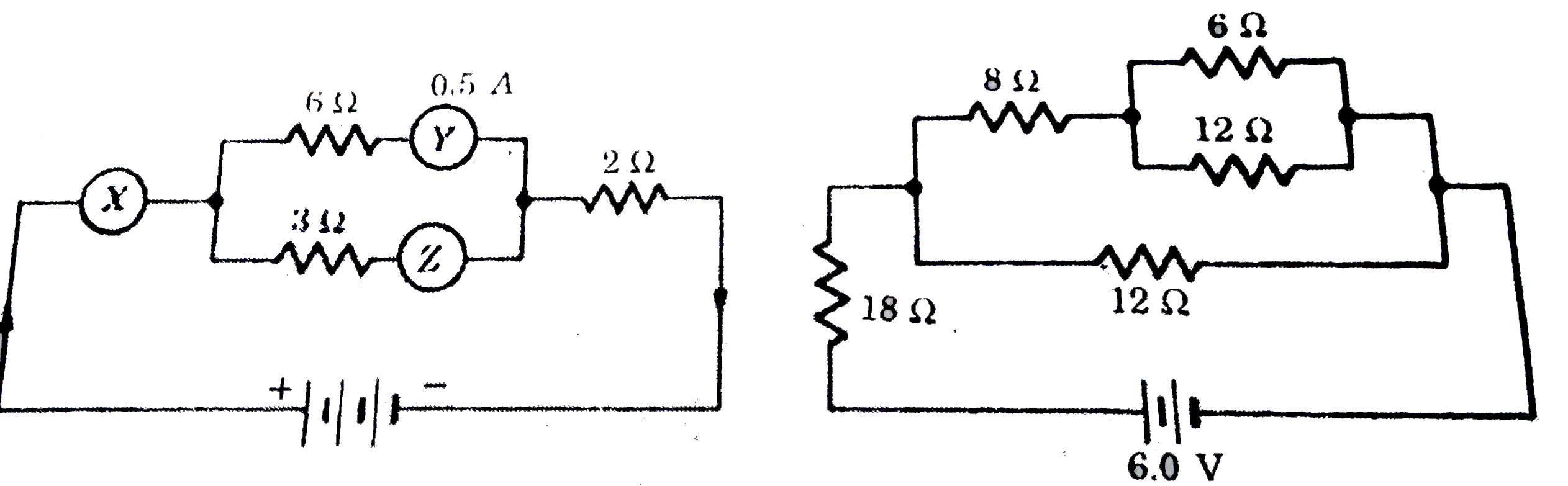
X, Y and Z are ammeters and Y reads 0.5 A. (i) What are the readings in ammeters X and Z ? (ii) What is the total resistance of the circuit ?
View SolutionIn the circuit shown in Fig. 4.63, the terminal voltage of the battery is 6.0 V. Find the current I through the `18 Omega` resistor.
View SolutionIn the circuit shown in Fig. 4.64, the battery has an emf of 12.0 V and an internal resistance of `5R//11`. If the ammeter reads 2.0 A, what is the value of R ?
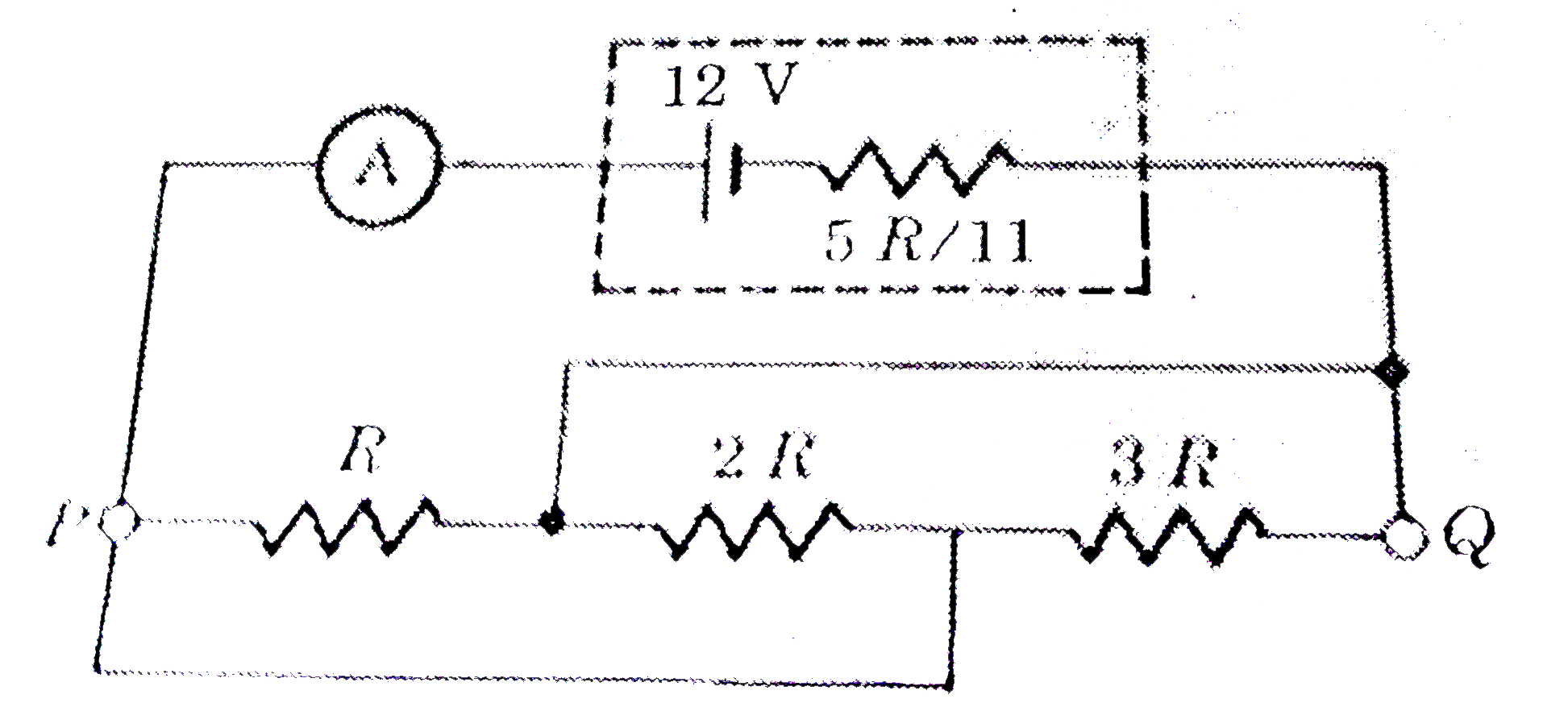
View SolutionFind the ammeter reading in the cirucit shown in Fig. 4.65.
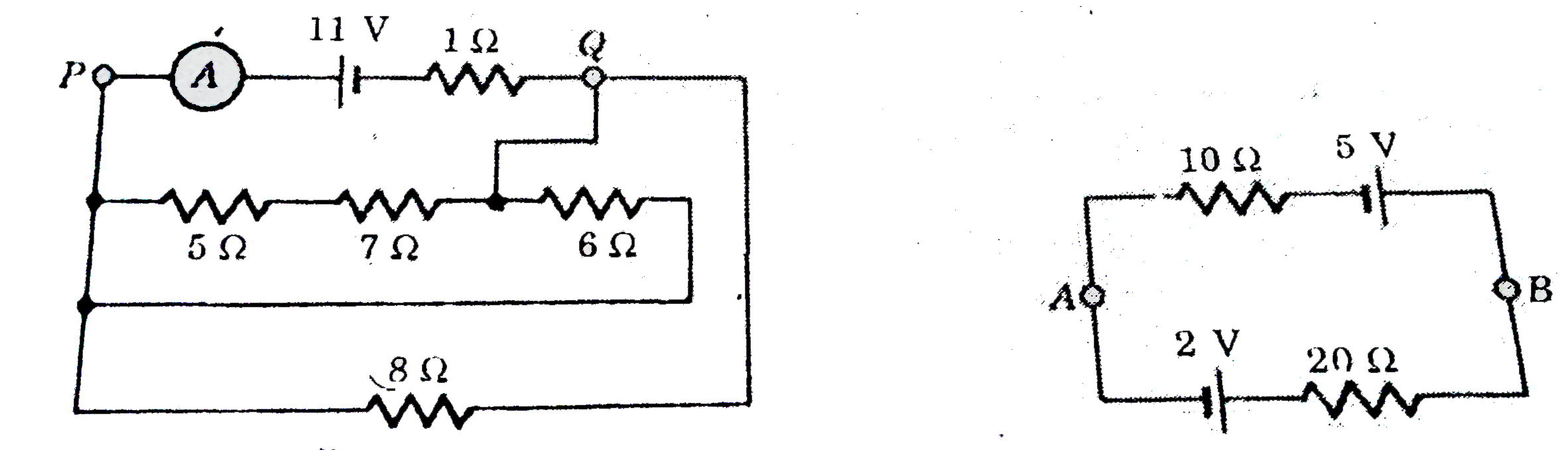
View SolutionFind the potential difference between the points A and B in the circuit shown in Fig. 4.66. Internal resistances of the cells are negligible.
View SolutionThe reading of a voltmoter when a cell is connected to it is 2.2 V. When the terminals of the cell are connected to a resistance of `4 Omega`, the voltmeter reading drops to 2 V. Find the internal resistance of the cell.
View SolutionThe potential difference across a cell is 1.8 V when a current of 0.5 A is drawn from it. The p.d. falls to 1.6 V when a current of 1.0 A is drawn. Find the emf and the internal resistance of the cell.
View SolutionThe potential difference of a cell in an open circuit is 6 V, which falls to 4 V when a current of 2 A is drawn from the cell. Calculate the emf and the internal resistance of the cell.
View SolutionIn the circuit shown in Fig. 4.67, the resistance of the ammeter A is negligible and that of thevoltmeter V is very high. When the switch S is open, the reading of voltmeter is 1.53 V. On closing the switch S, the reading of ammeter drops to 1.03 V. Calculate : (i) emf of the cell (ii) internal resistance of the cell (iii) value of R.
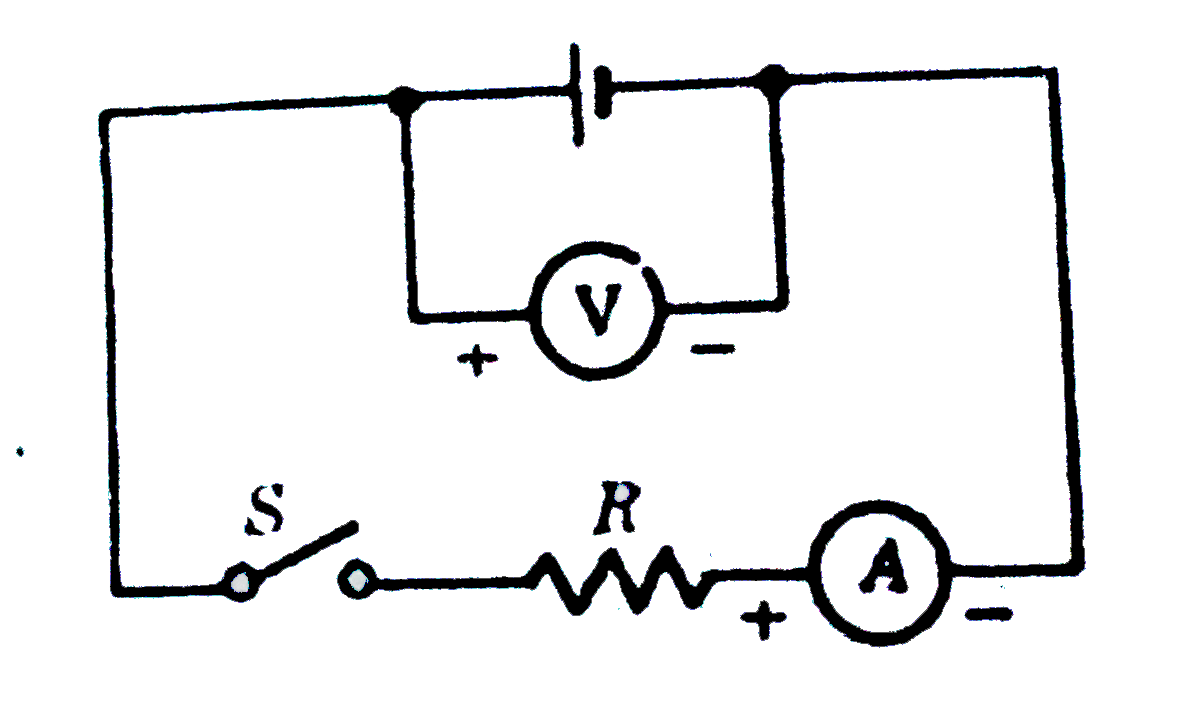
View SolutionThe potential differnce between the terminals of a battery of emf 6.0 V and internal resistance `1 Omega` drops to 5.8 V when connected across an external resistor . Find the resistance of the external res
View SolutionThe potenital difference between the terminals of a 6.0 V battery is 7.2 V when it is being charged by a current of 2.0 A. What is the internal resistance of the resistor.
View SolutionA battery of emf 2 V and internal resistance `0.5 Omega` is connected across a resistance of `9.5 Omega`. How many electrons pass through a cross-section of the resistance in 1 second ?
View SolutionWhen a resistance of `2 Omega` is placed across the terminals of a battery, the current is 0.5 A. When the resistance across the terminals of the battery is `5 Omega`, the current is 0.25 A. Calculate the emf of the battery and also its internal resistance.
View SolutionThe emf of a battery is 4.0 V and its internal resistance is `1.5 Omega`. Its potential difference is measured by a voltmeter of resistance `1000 Omega`. Calculate the percentage error in the reading of emf shown by voltmeter.
View Solution10 cells, each of internal resistance `0.5 Omega` and 1.2 V emf are connected (a) all in series and (b) all in paralle. Calculate the current sent in each case through a wire of resistance `0.8 Omega`.
View SolutionTwo cells of 1.5 V and 2 V , having internal resistances of `1Omega` and `2Omega` respectively, are connected in parallel so as to read the current in the same direction through an external resistance of `5 Omega` . The current in the external resistance will be
View SolutionThree identical, each of emf 2 V and internal resistance `0.2 Omega` are connected in series to an external resistor of `7.4 Omega`. Calculate the current in the circuit.
View SolutionThree identical cells each of emf 2 V and unknown internal resistance are connected in parallel. This combination is connected to a `5 Omega` resistor. If the terminal voltage across the cells is 1.5 V, what is the internal resistance of each cell ?
View SolutionIn the circuit shown in Fig. 4.68, the cells `epsilon_(1) " and " epsilon_(2)` have emf's of 4 V and 8 V and internal resistances of `0.5 Omega` and `1 Omega` respectively. Calculate the current in each resistance.
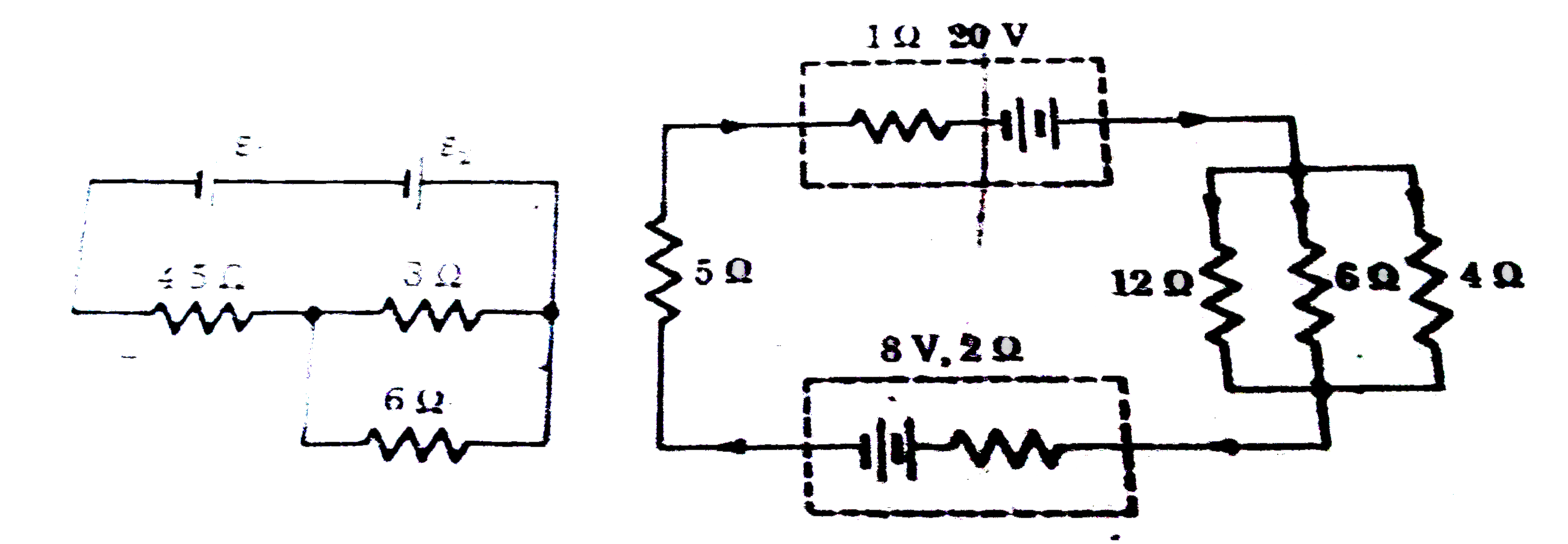
View SolutionA 20 V battery of internal resistance `1 Omega` is connected to three coils of `12 Omega, 6 Omega` and `4 Omega` in parallel, a resistor of `5Omega` and a reversed battery (emf=8 V and internal resistance `=2 Omega`), as shown in Fig. 4.69. Calculate the current in each resistor and the terminal potential difference across each battery.
View SolutionTwo cells connected in series have electromotive force of 1.5 V each. Their internal resistances are `0.5 Omega` and `0.25 Omega` respectively. This combination is connected to a resistance of `2.25 Omega`. Calculate the current flowing in the circuit and the potential differnce across the terminals of each cell.
View SolutionFind the minimum number of cells required to produce an electric current of 1.5 A through a resistance of `30 Omega`. Given that the emf of each cell is 1.5 V and internal resistance `1.0 Omega`.
View SolutionHow would you arrange 64 similar cells each having an emf of 2.0 V and internal resistance `2 Omega` so as to send maximum current through an external resistance of `8 Omega`.
View Solution
Problems For Self questions and complete solutions for chapter CURRENT ELECTRICITY of DHANPAT RAI & CO PHYSICS (HINGLISH) of Class 12